Open journal of Chemistry (OJC)

OJC, Volume 2018 Issue 2
Pages: 1
- 10

ISSN: 2618-0758 (Online) 2618-074X (Print)

DOI: https://www.doi.org/10.30538/psrp-ojc2018.0006

Research article

Calculating Degree Based Topological Indices of Line Graph of $HAC_{5}C_{6}C_{7}[p,q]$ Nanotube via M-Polynomial

Author(s): ^¹, ^¹

¹Department of Mathematics, The University of Lahore (Pakpattan Campus), Lahore Pakistan.

Copyright © Aziz ur Rehman, Waseem Khalid. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: 21/09/2018
Accepted: 14/11/2018
Published: 29/11/2018

Abstract

The application of graph theory in chemical and molecular structure research far exceeds people’s expectations, and it has recently grown exponentially. In the molecular graph, atoms are represented by vertices and bonded by edges. In this report, we study the M-polynomial of line graph of $HAC_{5}C_{6}C_{7}[p,q]$ and recover many degree-based topological indices from it.

Keywords: Line graph; Zagreb index; Molecular graph; Nanotube.

1. Introduction

Graph theory provides chemists with a variety of useful tools, such as topological indices. Molecular compounds are often modeled using molecular graphs. The molecular graph represents the structural formula of the compound in the form of graph theory, the vertices of which correspond to the atoms of the compound and the edges correspond to the chemical bonds [1].
Chemical informatics is a new area of research that integrates chemistry, mathematics, and information science. It studies the quantitative structure-activity (QSAR) and structure-property (QSPR) relationships [2, 3, 4, 5] used to predict the biological activity and properties of compounds. In the QSAR / QSPR study, the physical and chemical properties and topological indices such as Szeged index, Wiener index, Randi’c index, ABC index and Zagreb index etc were used to predict the biological activity of compounds. A molecular graph can be identified by topological index, polynomials, sequences or matrices [6].
The topological index is a number associated with the graph [7]. It represents the topological structure of the graph and is invariant under the automorphism of the graph. There are some major topological index categories, such as distance-based topological indices [8, 9], degree-based topological indices [10, 11], and counting-related polynomial and graph indices [7]. In these categories, the degree-based topological index is very important and plays a crucial role in chemical graph theory, especially in chemistry [12, 13, 14, 15]. More precisely, the topological index $Top(G)$ of the graph is a number with the following characteristics: If a graph $H$ is isomorphic to $G$, then $Top(H)= Top(G)$. The concept of topological index comes from Wiener [16]. When he studied the boiling point of paraffin, he named the index as the path number. Later, the path number was renamed Wiener index.
Carbon nanotubes form an interesting class of non-carbon materials [17]. There are three types of nanotubes, namely chiral, zigzag and armchairs nanotubes [18]. These carbon nanotubes show significant mechanical properties [17]. Experimental studies have shown that they belong to the most rigid and elastic known materials [19]. Diudea [20] was the first chemist to consider the topology of nanostructures.
$HAC_{5}C_{6}C_{7}[p,q] $ [21] shown in Figure 1 is constructed by alternating $C_{5}$, $C_{6}$ and $C_{7}$ carbon cycles. It is tube shaped material but we consider it in the form of sheet shown in Figure 2. The two dimensional lattice of $HAC_{5}C_{6}C_{7}[p,q]$ consists of $p$ rows and $q$ periods. Here $p$ denotes the number of pentagons in one row and $q$ is the number of periods in whole lattice. A period consist of three rows (See references [22, 23]). Figures are taken from [24]. Figure 3 is 2D graph of $HAC_{5}C_{6}C_{7}[p,q]$ and figure 4 is line graph of $HAC_{5}C_{6}C_{7}[p,q]$.

Figure 1. $HAC_{5}C_{6}C_{7}[p,q]$ Nanotube.

Figure 2. 2D graph of $HAC_{5}C_{6}C_{7}[p,q]$.

The aim of this paper is to compute M-polynomial of the line graph of $HAC_{5}C_{6}C_{7}[p,q]$-nanotube. We also recover many degree-based topological indices of the line graph of $HAC_{5}C_{6}C_{7}[p,q]$ nanotube from this M-polynomial. A line graph has many useful applications in physical chemistry [25, 26] and is defined as: the line graph $L(G)$ of a graph $G$ is the graph each of whose vertex represents an edge of $G$ and two of its vertices are adjacent if their corresponding edges are adjacent in $G$.

2. Basic definitions and Literature Review

Throughout this article, we take $G$ as a connected graph. $V(G)$ is the vertex set and $E(G)$ is the edge set. The degree of a vertex $v$ is denoted by

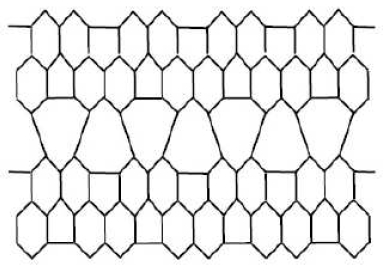
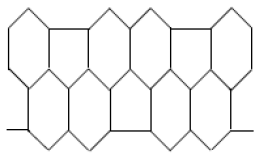
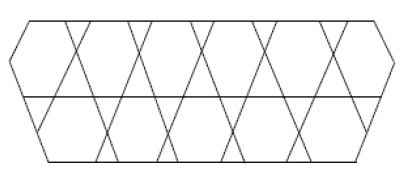
Dfinition 2.1.[27] The M-polynomial of $G$ is defined as: $$M(G, x,y)= \sum\limits_{\delta\leq i\leq j\leq \triangle}m_{ij}(G)x^{i}y^{j}$$ where $\delta= \min\{d_{v}: v\in V(G)\}$, $\triangle= \max\{d_{v}: v\in V(G)\}$ and $m_{ij}(G)$ is the edge $uv\in E(G)$ such that $d_{u}=i$ and $d_{v}=j$.

Wiener index and its various applications are discussed in [28, 29, 30]. Randić index, $R_{-\frac{1}{2}}(G)$, is introduced by Milan Randić in 1975 defined as: $R_{-\frac{1}{2}}(G)=\sum\limits_{uv\in E(G)}\frac{1}{\sqrt{d_{u}d_{v}}}$. For general details about $R_{-\frac{1}{2}}(G)$, and its generalized Randic index, $R_{\alpha}(G)=\sum\limits_{uv\in E(G)}\frac{1}{(d_{u}d_{v})^{\alpha}}$ please see [31, 32, 33, 34, 35]. The inverse Randić index is defined as $RR_{\alpha}(G)=\sum\limits_{uv\in E(G)}(d_{u}d_{v})^{\alpha}$ Clearly $R_{-\frac{1}{2}}(G)$ is a special case of $R_{\alpha}(G)$ when $\alpha=\frac{1}{2}$. This index has many applications in diverse areas. Many papers and books such as [36, 37, 38] are written on this topological index as well. Gutman and Trinajstić introduced two indices defined as: $M_{1}(G)=\sum\limits_{u\in V(G)}(d_{u}+d_{v})$ and $M_{2}(G)=\sum\limits_{uv\in E(G)}d_{u}\times d_{u}$. The second modified Zagreb index is defined as: $^{m}M_{2}(G)=\sum\limits_{uv\in E(G)}\frac{1}{d_{u}\times d_{u}}$. We refer [39, 40, 41, 42, 43] to the readers for comprehensive details of these indices. Other famous indices are Symmetric division index: $SDD(G) = \sum\limits_{uv\in E(G)}\left\{\frac{\min(d_{u},d_{v})}{\max(d_{u},d_{v})},\frac{\max(d_{u},d_{v})}{\min(d_{u},d_{v})}\right\}$ harmonic index: $H(G)=\sum\limits_{uv\in E(G)}\frac{2}{d_{u}+d_{v}}$ inverse sum index: $I(G)=\sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{d_{u}+d_{v}}$ and augmented Zagreb index: $A(G) = \sum\limits_{uv\in E(G)}\left\{\frac{\max(d_{u},d_{v})}{\max(d_{u},d_{v})}\right\}^{3}$ [39, 40, 41]. Tables presented in [44, 45, 46, 47, 48] relates some of these well-known degree-based topological indices with M-polynomial with following reserved notations Where $D_xf= x\frac{\partial(f(x,y))}{\partial x}, D_yf = y\frac{\partial(f(x,y))}{\partial y}, S_x = \int_0^x\frac{f(y,t)}{t}dt,$ $S_y = \int_0^y\frac{f(x,t)}{t}dt, j(f(x,y))=f(x,x), Q_{\alpha} (f(x,y))= x^{\alpha} f(x,y),$ for non zero ${\alpha},$ $j(f(x,y))= f(x,x)$

3. Computational Results

\noindent In this section, we give our computational results.

Theorem 3.1. Let $G$ be the line graph of $HAC_{5}C_{6}C_{7}[p,q]$ nanotube. Then the M-Polynomial of $G$ is \begin{equation} M(G,x,y)=2x^{2}y^{2}+12x^{2}y^{3}+(16p+1)x^{3}y^{3}+(12p+10)x^{3}y^{4}+(70p-37)x^{4}y^{4} \end{equation}

Proof. Let $G$ be the line graph of $HAC_{5}C_{6}C_{7}[p,q]$ nanotubes where $p$ denotes the number of pentagons in one row and $q$ denotes the number of periods in whole lattice . The edge set of line graph of $HAC_{5}C_{6}C_{7}[p,q]$ with $p\geq 1$ and $q=2$ has following five partitions,
$E_{2,2}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=2,d_v=2\}$
$E_{2,3}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=2,d_v=3\}$
$E_{3,3}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=3,d_v=3\}$
$E_{3,4}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=3,d_v=4\}$ and
$E_{4,4}= \{e=vu\in E(HAC_{5}C_{6}C_{7}[p,q])| d_u=4,d_v=4\}$.
Now, $$|E_{2,2}|=2$$ $$|E_{2,2}|=12$$ $$|E_{2,2}|=6p+1$$ $$|E_{2,2}|=12p+10$$ and $$|E_{2,2}|=70p-37$$ So, The M-polynomial of $(HAC_{5}C_{6}C_{7}[p,q])$ is equal to: \begin{eqnarray*} M(G,x,y)&=& \sum_{i \leq j} m_{ij}(G)x^i y^j\\ &=& \sum_{2\leq 2}m_{2,2}(G)x^2 y^2+ \sum_{2\leq 3}m_{2,3}(G)x^2 y^{3}\\ &&+\sum_{3\leq 3}m_{3,3}(G)x^3 y^3+ \sum_{3\leq 4}m_{3,4}(G)x^3 y^{4}\\ &&+\sum_{4\leq 4}m_{4,4}(G)x^4 y^4\\ &=& \sum_{E_{2,2}}m_{2,2}(G)x^2 y^2+ \sum_{E_{2,3}}m_{2,3}(G)x^2 y^{3}\\ &&+\sum_{E_{3,3}}m_{3,3}(G)x^3 y^3+ \sum_{E_{3,4}}m_{3,4}(G)x^3 y^{4}\\ &&+\sum_{E_{4,4}}m_{4,4}(G)x^4 y^4\\ &=& |E_{2,2}|x^2 y^2+ |E_{2,3}|x^2 y^{3}+|E_{3,3}|x^3 y^3+ |E_{3,4}|x^3 y^{4}\\ &&+|E_{4,4}|x^4 y^4\\ &=& 2x^{2}y^{2}+12x^{2}y^{3}+(16p+1)x^{3}y^{3}+(12p+10)x^{3}y^{4}\\ &&+(70p-37)x^{4}y^{4}. \end{eqnarray*}

Proposition 3.2. Let $G$ be the line graph of $(HAC_{5}C_{6}C_{7}[p,q])$ nanotube, then

$M_{1}(G)=2(85p-19)$
$M_{2}(G)=1318p-383$
$^{m}M_{2}(G)=\frac{145}{24}p+\frac{163}{144}$
$R_{\alpha}(G)=(2.3^{2\alpha+1}+2^{2(\alpha+1)}.3^{\alpha+1}+35.2^{4\alpha+1})p+(2^{2\alpha+1}+2^{\alpha+2}3^{\alpha+1}$
$(3^{2\alpha}+2^{2\alpha+1}.3^{\alpha}.5-37.2^{4\alpha})$
$RR_{\alpha}(G)=\left(\frac{2}{3^{2\alpha-1}}+\frac{1}{2^{2(\alpha-1)}.3^{\alpha-1}}+\frac{35}{2^{4\alpha+1}}\right)p+(\frac{1}{2^{2\alpha-1}}+\frac{1}{2^{\alpha-2}3^{\alpha-1}}$
$\frac{1}{3^{2\alpha}}+\frac{5}{2^{2\alpha-1}.3^{\alpha}}-\frac{37}{2^{4\alpha}})$
$SSD(G)=177p+\frac{127}{6}.$
$H(G)=\frac{321}{14}p+\frac{109}{420}$
$I(G)=\frac{1187}{7}p+\frac{2727}{70}$
$A(G)=\frac{168657029}{108000}p-\frac{19007957}{43200}$

Proof. Let $$M(G,x,y)=2x^{2}y^{2}+12x^{2}y^{3}+(16p+1)x^{3}y^{3}+(12p+10)x^{3}y^{4}+(70p-37)x^{4}y^{4}$$ Then, $$D_{x}f(x,y)=4x^{2}y^{2}+24x^{2}y^{3}+3(16p+1)x^{3}y^{3}+3(12p+10)x^{3}y^{4}+4(70p-37)x^{4}y^{4}.$$ $$D_{y}f(x,y)=4x^{2}y^{2}+36x^{2}y^{3}+3(16p+1)x^{3}y^{3}+4(12p+10)x^{3}y^{4}+4(70p-37)x^{4}y^{4}.$$ $$D_{y}D_{x}f(x,y)=8x^{2}y^{2}+72x^{2}y^{3}+9(6p+1)x^{3}y^{3}+12(12p+10)x^{3}y^{4}+16(70p-37)x^{4}y^{4}.$$ $$S_{x}S_{y}f(x,y)=\frac{1}{2}x^{2}y^{2}+2x^{2}y^{3}+\frac{1}{9}(16p+1)x^{3}y^{3}+\frac{1}{12}(12p+10)x^{3}y^{4}+\frac{1}{16}(70p-37)x^{4}y^{4}.$$ $$D_{x}^{\alpha}D_{y}^{\alpha}f(x,y)=2^{2\alpha+1}x^{2}y^{2}+2^{\alpha+2}3^{\alpha+1}x^{2}y^{3}+3^{2\alpha}(16p+1)x^{3}y^{3}+3^{\alpha}4^{\alpha}(12p+10)x^{3}y^{3}+4^{2\alpha}(70p-37)x^{3}y^{3}.$$ $$S_{x}^{\alpha}S_{y}^{\alpha}f(x,y)=\frac{1}{2^{2\alpha-1}}x^{2}y^{2}+\frac{1}{2^{\alpha-2}3^{\alpha-1}}x^{2}y^{3}+\frac{1}{3^{2\alpha}}(16p+1)x^{3}y^{3}+\frac{1}{3^{\alpha}4^{\alpha}}(12p+10)x^{3}y^{4}+\frac{1}{4^{2\alpha}}(70p-37)x^{4}y^{4}.$$ $$S_{y}D_{x}f(x,y)=2x^{2}y^{2}+8x^{2}y^{3}+(16p+1)x^{3}y^{3}+\frac{3}{4}(12p+10)x^{3}y^{3}+(70p-37)x^{4}y^{4}.$$ $$S_{x}D_{y}f(x,y)=2x^{2}y^{2}+18x^{2}y^{3}+(16p+1)x^{3}y^{3}+\frac{3}{4}(12p+10)x^{3}y^{3}+(70p-37)x^{4}y^{4}.$$ $$S_{x}Jf(x,y)=\frac{1}{2}x^{4}+\frac{12}{5}x^{5}+\frac{9}{6}(6p+1)x^{6}+\frac{12}{7}(12P+10)x^{7}+2(70p-37)x^{8}.$$ $$S_{x}JD_{y}D_{x}f(x,y)f(x,y)=16x^{4}+\frac{72}{5}x^{5}+\frac{9}{6}(6p+1)x^{6}+\frac{12}{7}(12P+10)x^{7}+2(70p-37)x^{8}.$$ $$S_{x}^{3}Q_{-2}JD_{x}^{3}D_{y}^{3}f(x,y)=16x^{2}+96x^{3}+\frac{729}{64}(6p+1)x^{4}+\frac{1728}{125}(12P+10)x^{5}+\frac{4096}{216}(70p-37)x^{6}.$$

1. First Zagreb Index $$M_{1}(G)=(Dx+Dy)[f(x,y)]_{y=x=1}= 2(85p-19)$$

2. Second Zagreb Index $$M_{2}(G)=(Dx\cdot Dy)[f(x,y)]_{y=x=1}=1318p-383$$

3. Second Modified Zagreb Index $$^{m}M_{2}(G)=(SxSy)[f(x,y)]_{x=y=1}=^{m}M_{2}(G)=\frac{145}{24}p+\frac{163}{144}$$

4. Randic Index \begin{eqnarray*} R_{\alpha}(G)=(D_x^{\alpha}D_y^{\alpha})[f(x,y)]_{y=x=1}&=&(2.3^{2\alpha+1}+2^{2(\alpha+1)}.3^{\alpha+1}+35.2^{4\alpha+1})p\\ &&+(2^{2\alpha+1}+2^{\alpha+2}3^{\alpha+1}(3^{2\alpha}\\ &&+2^{2\alpha+1}.3^{\alpha}.5-37.2^{4\alpha}) \end{eqnarray*}

5. General Randic Index \begin{eqnarray*} RR_{\alpha}(G)=(S_x^{\alpha} S_y^{\alpha})[f(x,y)]_{x=y=1}&=&\left(\frac{2}{3^{2\alpha-1}}+\frac{1}{2^{2(\alpha-1)}.3^{\alpha-1}}+\frac{35}{2^{4\alpha+1}}\right)p\\ &&+(\frac{1}{2^{2\alpha-1}}+\frac{1}{2^{\alpha-2}3^{\alpha-1}}\frac{1}{3^{2\alpha}}\\ &&+\frac{5}{2^{2\alpha-1}.3^{\alpha}}-\frac{37}{2^{4\alpha}}) \end{eqnarray*}

6. Symmetric Division Index $$SSD(G)=(D_x S_y+ D_y S_x)[f(x,y)]=177p-\frac{127}{6}$$

7. Harmonic Index $$H(G)=2S_x J[f(x,y)]_{y=x=1}=\frac{321}{14}p+\frac{109}{420}$$

8. Inverse Sum Index $$I(G)=S_x [J(D_x D_y)][f(x,y)]_{y=x=1}=\frac{1187}{7}p+\frac{2727}{70}$$

9. Augmented Zagreb Index $$A(G)=S_x^3 Q_{-2} J D_x^3 D_y^3[f(x,y)]_{x=y=1}=\frac{168657029}{108000}p-\frac{19007957}{43200}$$

4. Conclusion

In the present article, we computed closed form of M-polynomial for the line graph of $HAC_{5}C_{6}C_{7}[p,q]$ and then we derived many degree-based topological indices as well. Topological indices thus calculated can help us to understand the physical features, chemical reactivity, and biological activities. In this point of view, a topological index can be regarded as a score function which maps each molecular structure to a real number and is used as descriptors of the molecule under testing. These results can also play a vital part in the determination of the significance of silicon-carbon in electronics and industry. For example Randic index is useful for determining physio-chemical properties of alkanes as noticed by chemist Melan Randic in 1975. He noticed the correlation between the Randic index R and several physico-chemical properties of alkanes like, enthalpies of formation, boiling points, chromatographic retention times, vapor pressure and surface areas.

Competing Interests

The author do not have any competing interests in the manuscript.

References:

Devillers, J., & Balaban, A. T. (Eds.). (2000). Topological indices and related descriptors in QSAR and QSPAR. CRC Press. [Google Scholor]
Karelson, M. (2000). Molecular descriptors in QSAR/QSPR. Wiley-Interscience. [Google Scholor]
Karelson, M., Lobanov, V. S., & Katritzky, A. R. (1996). Quantum-chemical descriptors in QSAR/QSPR studies. Chemical reviews, 96(3), 1027-1044. [Google Scholor]
Consonni, V., Todeschini, R., Pavan, M., & Gramatica, P. (2002). Structure/response correlations and similarity/diversity analysis by GETAWAY descriptors. 2. Application of the novel 3D molecular descriptors to QSAR/QSPR studies. Journal of chemical information and computer sciences, 42(3), 693-705. [Google Scholor]
Ferguson, A. M., Heritage, T., Jonathon, P., Pack, S. E., Phillips, L., Rogan, J., & Snaith, P. J. (1997). EVA: A new theoretically based molecular descriptor for use in QSAR/QSPR analysis. Journal of computer-aided molecular design, 11(2), 143-152. [Google Scholor]
Balaban, A. T., Motoc, I., Bonchev, D., & Mekenyan, O. (1983). Topological indices for structure-activity correlations. In Steric effects in drug design (pp. 21-55). Springer, Berlin, Heidelberg. [Google Scholor]
Balaban, A. T. (1983). Topological indices based on topological distances in molecular graphs. Pure and Applied Chemistry, 55(2), 199-206. [Google Scholor]
Balaban, A. T. (1982). Highly discriminating distance-based topological index. Chemical Physics Letters, 89(5), 399-404. [Google Scholor]
Xu, K., Liu, M., Das, K. C., Gutman, I., & Furtula, B. (2014). A survey on graphs extremal with respect to distance-based topological indices. MATCH Commun. Math. Comput. Chem, 71(3), 461-508. [Google Scholor]
Gutman, I. (2013). Degree-based topological indices. Croatica Chemica Acta, 86(4), 351-361. [Google Scholor]
Furtula, B., Gutman, I., & Dehmer, M. (2013). On structure-sensitivity of degree-based topological indices. Applied Mathematics and Computation, 219(17), 8973-8978. [Google Scholor]
Gutman, I., Furtula, B., & Elphick, C. (2014). Three new/old vertex-degree-based topological indices. MATCH Commun. Math. Comput. Chem, 72(3), 617-632. [Google Scholor]
Rada, J., Cruz, R., & Gutman, I. (2014). Benzenoid systems with extremal vertex-degree-based topological indices. MATCH Commun. Math. Comput. Chem, 72(1), 125-136. [Google Scholor]
Deng, H., Yang, J., & Xia, F. (2011). A general modeling of some vertex-degree based topological indices in benzenoid systems and phenylenes. Computers & Mathematics with Applications, 61(10), 3017-3023. [Google Scholor]
Hayat, S., & Imran, M. (2015). On degree based topological indices of certain nanotubes. Journal of Computational and Theoretical Nanoscience, 12(8), 1599-1605. [Google Scholor]
Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20. [Google Scholor]
Dresselhaus, G., & Riichiro, S. (1998). Physical properties of carbon nanotubes. World Scientific. [Google Scholor]
Chae, H. G., Sreekumar, T. V., Uchida, T., \& Kumar, S. (2005). A comparison of reinforcement efficiency of various types of carbon nanotubes in polyacrylonitrile fiber. Polymer, 46(24), 10925-10935. [Google Scholor]
Thostenson, E. T., Ren, Z., & Chou, T. W. (2001). Advances in the science and technology of carbon nanotubes and their composites: a review. Composites science and technology, 61(13), 1899-1912. [Google Scholor]
Diudea, M. V., & Gutman, I. (1998). Wiener-type topological indices. Croatica Chemica Acta, 71(1), 21-51. [Google Scholor]
Farahani, M. R. (2012). The first and second Zagreb indices, first and second Zagreb polynomials of $HAC_{5}C_{6}C_{7}[p, q]$ And $HAC_{5}C_{7}[p, q]$ nanotubes. International Journal of Nanoscience and Nanotechnology, 8(3), 175-180. [Google Scholor]
Farahani, M. R. (2013). On the geometric-arithmetic and atom bond connectivity index of $HAC_{5}C_{6}C_{7}[p, q]$ nanotube. hemical Physics Research Journal, 6(1), 21-26. [Google Scholor]
Farahani, M. R. (2013). Atom bond connectivity and geometric-arithmetic indices Of $HAC_{5}C_{6}C_{7}[p, q]$ nanotube. Int. J. Chemical Modeling, 5(1), 127-132. [Google Scholor]
Yang, H., Sajjad, W., Baig, A. Q., \& Farahani, M. R. (2017). The Edge Version of Randic, Zagreb, Atom Bond Connectivity and Geometric-Arithmetic Indices of NA (Q)(P) Nanotube. International journal of advanced biotechnology and research, 8(2), 1582-1589. [Google Scholor]
Gutman, I., & Estrada, E. (1996). Topological indices based on the line graph of the molecular graph. Journal of chemical information and computer sciences, 36(3), 541-543. [Google Scholor]
Estrada, E., Guevara, N., & Gutman, I. (1998). Extension of edge connectivity index. Relationships to line graph indices and QSPR applications. Journal of chemical information and computer sciences, 38(3), 428-431. [Google Scholor]
Das, K. C., Xu, K., & Nam, J. (2015). Zagreb indices of graphs. Frontiers of Mathematics in China, 10(3), 567-582. [Google Scholor]
Yang, X., Ding, Y., & Ni, J. (2008). Ab initio prediction of stable boron sheets and boron nanotubes: structure, stability, and electronic properties. Physical Review B, 77(4), 041402. [Google Scholor]
Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20. [Google Scholor]
Dobrynin, A. A., Entringer, R., & Gutman, I. (2001). Wiener index of trees: theory and applications. Acta Applicandae Mathematica, 66(3), 211-249. [Google Scholor]
Randic, M. (1975). Characterization of molecular branching. Journal of the American Chemical Society, 97(23), 6609-6615. [Google Scholor]
Bollobás, B., & Erdös, P. (1998). Graphs of extremal weights. Ars Combinatoria, 50, 225-233.[Google Scholor]
Amić, D., Bešlo, D., Lučić, B., Nikolić, S., & Trinajstić, N. (1998). The vertex-connectivity index revisited. Journal of chemical information and computer sciences, 38(5), 819-822.[Google Scholor]
Hu, Y., Li, X., Shi, Y., Xu, T., & Gutman, I. (2005). On molecular graphs with smallest and greatest zeroth-order general Randic index. MATCH Commun. Math. Comput. Chem., 54(2), 425-434. [Google Scholor]
Caporossi, G., Gutman, I., Hansen, P., & Pavlović, L. (2003). Graphs with maximum connectivity index. Computational Biology and Chemistry, 27(1), 85-90. [Google Scholor]
Li, X., & Gutman, I. (2006). Mathematical Chemistry Monographs No. 1. Kragujevac.[Google Scholor]
Kier, L. B., & Hall, L. H. (1976). Medicinal Chemistry: Molecular Connectivity In Chemistry And Drug Research. Academic Press. [Google Scholor]
Kier, L. B., & Hall, L. H. (1986). Molecular connectivity in structure-activity analysis. Research Studies. [Google Scholor]
Gutman, I., Furtula, B., & Elphick, C. (2014). Three new/old vertex-degree-based topological indices. MATCH Commun. Math. Comput. Chem., 72(3), 617-632. [Google Scholor]
Nikolić, S., Kovačević, G., Miličević, A., & Trinajstić, N. (2003). The Zagreb indices 30 years after. Croatica chemica acta, 76(2), 113-124. [Google Scholor]
Gutman, I., & Das, K. C. (2004). The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem., 50(1), 83-92.[Google Scholor]
Das, K. C., & Gutman, I. (2004). Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem., 52(1), 103-112. [Google Scholor]
Ramane, H. S., & Jummannaver, R. B. (2016). Note on forgotten topological index of chemical structure in drugs. Applied Mathematics and Nonlinear Sciences, 1(2), 369-374.
Munir, M., Nazeer, W., Rafique, S., & Kang, S. M. (2016). M-polynomial and related topological indices of Nanostar dendrimers. Symmetry, 8(9), 97. [Google Scholor]
Munir, M., Nazeer, W., Rafique, S., Nizami, A. R., & Kang, S. M. (2016). M-polynomial and degree-based topological indices of titania nanotubes. Symmetry, 8, 117.
Munir, M., Nazeer, W., Rafique, S., & Kang, S. M. (2017). M-polynomial and degree-based topological indices of V-phenalinic nanotubes and nanotori, Scientific Reports, 7, 8756.
Munir, M., Nazeer, W., Rafique, S., Nizami, A. R., \& Kang, S. M. (2016). Some Computational Aspects of Triangular Boron Nanotubes. Symmetry, 9, 6.
Munir, M., Nazeer, W., Rafique, S., & Kang, S. M. (2016). M-Polynomial and Degree-Based Topological Indices of Polyhex Nanotubes. Symmetry 2016, 8, 149.

Open journal of Chemistry (OJC)

Calculating Degree Based Topological Indices of Line Graph of \(HAC_{5}C_{6}C_{7}[p,q]\) Nanotube via M-Polynomial