Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2019.0016
M-polynomial of some cactus chains and their topological indices
Department of Mathematics, Karnatak University, Dharwad-580003, Karnataka, India.;(B.B & A.P.B)
\(^{1}\)Corresponding Author: b.basavanagoud@gmail.com
Abstract
Keywords:
1. Introduction
The concept of degree is analogous to the concept of valence in organic chemistry with a limitation that degree of any vertex in any chemical graph is at most 4. This gives graph theory a broad way to chemistry. It is always interesting to find some properties of graphs or molecular graphs which are invariant. Topological indices and polynomials are foremost among them. Over the last decade there are numerous research papers devoted to topological indices and polynomials. Several topological indices have been defined in the literature. For various topological indices one can refer to [1, 2, 3, 4, 5, 6, 7,8].
Let \(G=(V,E)\) be a simple, undirected graph. Let \(V(G)\) be the vertex set and \(E(G)\) be the edge set of the graph \(G\), respectively. The degree \(d_G(v)\) of a vertex \(v\in V(G)\) is the number of edges incident to it in \(G\). Let \(\{v_1,v_2,...,v_n\}\) be the vertices of \(G\) and let \(d_i=d_G(v_i)\). A graph \(G\) is said to be \(r-\) regular if degree of each vertex in \(G\) is \(r\). A graph is called cycle if it is \(2-\) regular. A cactus graph is a connected graph in which any two simple cycles have at most one vertex in common. Every cycle of cactus graph is chordless and every block of a cactus graph is either an edge or a cycle. If all blocks of a cactus graph are triangular then it is called triangular cacti. If all the triangles of a triangular cactus graph has at most two cut-vertices and each cut-vertex is shared by exactly two triangles then we say that triangular cactus graph is a chain triangular cactus. In chain triangular cactus if we replace triangles by cycles of length 4 then we obtain cacti whose every block is \(C_{4}\), such cacti are called square cacti. For ortho-chain square cactus the cut vertices are adjacent and a para-chain square cactus their cut vertices are not adjacent. Recent study on some cactus chain can be found in [9, 10, 11] and references cited therein. For undefined graph theoretic terminology used in this paper can be found in [12].
The general form of degree-based topological index of a graph is given by $$TI(G)=\sum_{e=uv\in G}f(d_G(u),d_G(v))$$ where \(f=f(x,y)\) is a function appropriately chosen for the computation. Table 1 gives the standard topological indices defined by \(f(x,y)\).
The \(M-polynomial\) [13] was introduced in 2015 by Deutch and Klav\(\check{\text{z}}\)ar and is found useful in determining many degree-based topological indices (listed in Table 1).Definition 1.[13] Let \(G\) be a graph. Then \(M-polynomial\) of \(G\) is defined as $$M(G;x,y)=\sum _{i\le j}m_{ij}(G)x^iy^j,$$ where \(m_{ij}, i, j\ge1\), is the number of edges \(uv\) of \(G\) such that \(\{d_G(u), d_G(v)\}=\{i,j\}\) [14].
Recently, the study of \(M-polynomial\) are reported in [15, 16, 17, 18, 19]. The Table 1 was given by Deutch and Klav\(\check{\text{z}}\)ar to derive degree based topological indices from the \(M-\) polynomial.Table 1. [13] Derivation of some degree-based topological indices from \(M-\)polynomial.
| Notation | Topological Index | \(f(x,y)\) | Derivation from \(M(G;x,y)\) |
|---|---|---|---|
| \(M_1(G)\) | First Zagreb | \(x+y\) | \((D_x+D_y)(M(G;x,y)) |_{x=y=1}\) |
| \(M_2(G)\) | Second Zagreb | \(xy\) | \((D_xD_y)(M(G;x,y)) |_{x=y=1}\) |
| \(^{m}M_2(G)\) | Second modified Zagreb | \(\frac{1}{xy}\) | \((S_xS_y)(M(G;x,y)) |_{x=y=1}\) |
| \(S_{D}(G)\) | Symmetric division index | \(\frac{x^2+y^2}{xy}\) | \((D_xS_y+D_yS_x)(M(G;x,y)) |_{x=y=1}\) |
| \(H(G)\) | Harmonic | \(\frac{2}{x+y}\) | \(2S_xJ(M(G;x,y)) |_{x=1}\) |
| \(I_{n}(G)\) | Inverse sum index | \(\frac{xy}{x+y}\) | \(S_xJD_xD_y(M(G;x,y)) |_{x=1}\) |
| \(R_{\alpha}(G)\) | General Randi\'{c} index | \((xy)^\alpha\) | \(D_xD_y(M(G;x,y)) |_{x=y=1}\) |
Table 2.[20] New operator to derive degree-based topological indices from \(M-polynomial\).
| Notation | Topological Index | \(f(x,y)\) | Derivation from \(M(G;x,y)\) |
|---|---|---|---|
| \(\chi_{\alpha}(G)\) | General sum connectivity [7] | \((x+y)^\alpha\) | \(D^{\alpha}_x(J(M(G;x,y))) |_{x=1}\) |
| \(M^{\alpha}_1(G)\) | First general Zagreb [21] | \(x^{\alpha-1}+y^{\alpha-1}\) | \((D^{\alpha-1}_x+D^{\alpha-1}_y)(M(G;x,y)) |_{x=y=1}\) |
Note 2. Taking \(\alpha=2,3\) in first general Zagreb index, first Zagreb and forgotten \((F-index)\) topological indices are obtained respectively. The general Zagreb index or \((a,b)-\) Zagreb index was introduced by Azari et al. [22], which is a generalized version of vertex-degree-based topological index and is defined as $$M_{(a,b)}(G)=\sum _{uv\in E(G)} (d_{G}(u)^{a} d_{G}(v)^{b}+d_{G}(u)^{b}d_{G}(v)^{a}).$$ The importance of general Zagreb index is that from this index, one can derive seven more topological indices as given in [9]. But in fact, general Zagreb index can also be obtained from the \(M-\)polynomial with suitable operator, which we present in the Table 3.
Table 3. Operator to derive general Zagreb index from \(M-polynomial\).
| Notation | Topological Index | \(f(x,y)\) | Derivation from \(M(G;x,y)\) |
|---|---|---|---|
| \(M_{(a,b)}(G)\) | General Zagreb index [22] | \(x^{a}y^{b}+x^{b}y^{a}\) | \((D^{a}_xD^{b}_y+D^{b}_xD^{a}_y)(M(G;x,y)) |_{x=y=1}\) |
2. \(M-\)Polynomials of cactus chains
In this section, we obtain \(M-\) polynomials of two general cactus chains namely para cacti chain and ortho-cacti chain of cycles. We first compute \(M-\) polynomial of para cacti chain of cycles denoted by \(C^{n}_{m}\) where \(m\) is the length of each cycle and \(n\) is the length of the chain. Every block in \(C^{n}_{m}\) is a cycle \(C_{m}\).
The following theorem gives the \(M-\) polynomial of \(C^{n}_{m}.\)Theorem 2. Let \(C^{n}_{m}\) be para cacti chain of cycles for \(m\ge 3, n\ge 2.\) Then \begin{eqnarray*} M(C^{n}_{m};x,y)&=&(mn-4n+4)x^2y^2+4(n-1)x^2y^4. \end{eqnarray*}
Proof. The para cacti chain of cycles \(C^{n}_{m}\) has \(mn-n+1\) vertices and \(mn\) edges. The edge set of \(C^{n}_{m}\) can be partitioned as, \begin{eqnarray*} |E_{\{2,2\}}|&=&|\{uv\in E(C^{n}_{m}): d_{C^{n}_{m}}(u)=2 \;\; and \;\; d_{C^{n}_{m}}(v)=2\}|=(mn-4n+4).\\ |E_{\{2,4\}}|&=&|\{uv\in E(C^{n}_{m}): d_{C^{n}_{m}}(u)=2 \;\; and \;\; d_{C^{n}_{m}}(v)=4\}|=4(n-1). \end{eqnarray*} Thus, by using definition of \(M-polynomial\) we have, $$ M(C^{n}_{m};x,y)=(mn-4n+4)x^2y^2+4(n-1)x^2y^4. $$
Corollary 3. Let \(C^{n}_{m}\) be para cacti chain of cycles for \(m\ge 3, n\ge 2.\) Then $$M_{a,b}(C^{n}_{m})=2(mn-4n+4)2^{a+b}+4(n-1)2^{a+b}(2^{a}+2^{b}).$$
Proof. To derive general Zagreb index from \(M-\)polynomial we use the operator given in Table 3. Now, \begin{eqnarray*} M_{a,b}(C^{n}_{m})&=&(D^{a}_xD^{b}_y+D^{b}_xD^{a}_y)(M(C^{n}_{m};x,y)) |_{x=y=1}\\ &=& (D^{a}_xD^{b}_y+D^{b}_xD^{a}_y)((mn-4n+4)x^2y^2+4(n-1)x^2y^4)|_{x=y=1}\\ &=& (D^{a}_xD^{b}_y)((mn-4n+4)x^2y^2+4(n-1)x^2y^4)\\&&+(D^{b}_xD^{a}_y)((mn-4n+4)x^2y^2+4(n-1)x^2y^4)|_{x=y=1}\\ &=&2(mn-4n+4)2^{a+b}+4(n-1)2^{a+b}(2^{a}+2^{b}). \end{eqnarray*}
The expression obtained above, i.e., $$M_{a,b}(C^{n}_{m})=2(mn-4n+4)2^{a+b}+4(n-1)2^{a+b}(2^{a}+2^{b})$$ is same expression obtained in [9], Theorem 1. This shows that the \(M-\)polynomial has an extra advantage than the general Zagreb index as one can derive about 10 (listed in Tables 1, 2 and 3) degree-based topological indices from the \(M-\)polynomial including general Zagreb index so far. The following corollary gives the several topological indices of para cacti chain of cycles derived from \(M-\)polynomial.Corollary 4. Let \(C^{n}_{m}\) be para cacti chain of cycles for \(m\ge 3, n\ge 2.\) Then
- \(M_1(C^{n}_{m})=4mn+8n-8.\)
- \(M_2(C^{n}_{m})=4mn+16n-16.\)
- \(^{m}M_2(C^{n}_{m})= \frac{mn-2n+2}{4}.\)
- \(S_{D}(C^{n}_{m})= 2mn+2n-2.\)
- \(H(C^{n}_{m})=\frac{3mn-8n-8}{6}.\)
- \(I_{n}(C^{n}_{m})= \frac{3mn+4n-4}{3}.\)
- \(\chi_{\alpha}(C^{n}_{m})=(mn-4n+4)4^{\alpha}+4(n-1)6^{\alpha}.\)
- \(M^{\alpha}_{1}(C^{n}_{m})=(mn-4n+4)2^{\alpha}+(n-1)2^{2\alpha+1}(2^{\alpha-1}+1).\)
- \(R_{\alpha}(C^{n}_{m})=(mn-4n+4)2^{2\alpha}+(n-1)2^{3\alpha+2}.\)
Proof. Using the above Theorem 2 and column 4 of Table 1, we get the desired results.
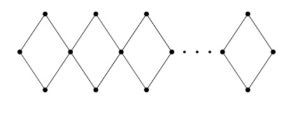
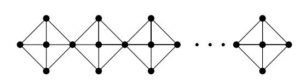
Figure 1. Para-chain square cactus \(Q_{n}\)
Corollary 5. Let \(Q_{n}\) be para-chain square cactus graph for \( n\ge 2.\) Then \begin{eqnarray*} M(Q_{n};x,y)&=&4x^2y^2+4(n-1)x^2y^4. \end{eqnarray*}
Proof. Taking \(m=4\) in the Theorem 2, we get the desired result.
Corollary 6. Let \(Q_{n}\) be para-chain square cactus graph for \( n\ge 2.\) Then
- \(M_1(Q_{n})=24n-8.\)
- \(M_2(Q_{n})=32n-16.\)
- \(^{m}M_2(Q_{n})= \frac{n+1}{2}.\)
- \(S_{D}(Q_{n})= 10n-2.\)
- \(H(Q_{n})=\frac{4n-8}{6}.\)
- \(I_{n}(Q_{n})=\frac{16n-4}{3}.\)
- \(\chi_{\alpha}(Q_{n})=4^{\alpha+1}+4(n-1)6^{\alpha}.\)
- \(M^{\alpha}_{1}(Q_{n})=2^{\alpha+2}+(n-1)2^{2\alpha+1}(2^{\alpha-1}+1).\)
- \(R_{\alpha}(Q_{n})=2^{2\alpha+2}+(n-1)2^{3\alpha+2}.\)
Figure 2. Para-chain hexagonal cactus graph \(L_{n}.\)
Corollary 7. Let \(Q_{n}\) be para-chain square cactus graph for \( n\ge 2.\) Then \begin{eqnarray*} M(Q_{n};x,y)&=&(2n+4)x^2y^2+4(n-1)x^2y^4. \end{eqnarray*}
Proof. Taking \(m=6\) in the Theorem 2, we get the desired result.
Corollary 8. Let \(L_{n}\) be para-chain hexagonal cactus graph for \( n\ge 3.\) Then
- \(M_1(L_{n})=32n-8.\)
- \(M_2(L_{n})=40n-16.\)
- \(^{m}M_2(L_{n})= \frac{2n+1}{2}.\)
- \(S_{D}(L_{n})= 14n-2.\)
- \(H(L_{n})=\frac{5n-4}{3}.\)
- \(I_{n}(L_{n})=\frac{22n-4}{3}.\)
- \(\chi_{\alpha}(L_{n})=(2n+4)4^{\alpha}+4(n-1)6^{\alpha}.\)
- \(M^{\alpha}_{1}(L_{n})=(2n+4)2^{\alpha}+(n-1)2^{2\alpha+1}(2^{\alpha-1}+1).\)
- \(R_{\alpha}(L_{n})=(2n+4)2^{2\alpha}+(n-1)2^{3\alpha+2}.\)
Theorem 9. Let \(CO^{n}_{m}\) be ortho cacti chain of cycles for \(m\ge 3, n\ge 2.\) Then \begin{eqnarray*} M(CO^{n}_{m};x,y)&=&(mn-3n+2)x^2y^2+2nx^2y^4+(n-1)x^4y^4. \end{eqnarray*}
Proof. The \(CO^{n}_{m}\) be ortho-chain cacti of cycles has \(mn-n+1\) vertices and \(mn\) edges. The edge partition of \(CO^{n}_{m}\) is given by, \begin{eqnarray*} E_{\{2,2\}}&=&{\{uv\in E(CO^{n}_{m}): d_{CO^{n}_{m}}(u)=2 \;\; and \;\; d_{CO^{n}_{m}}(v)=2\}},\\ E_{\{2,4\}}&=&{\{uv\in E(CO^{n}_{m}): d_{CO^{n}_{m}}(u)=2 \;\; and \;\; d_{CO^{n}_{m}}(v)=4\}},\\ E_{\{4,4\}}&=&{\{uv\in E(CO^{n}_{m}): d_{CO^{n}_{m}}(u)=4 \;\; and \;\; d_{CO^{n}_{m}}(v)=4\}},\\ \text{Now,}\;\; |E_{\{2,2\}}|&=&mn-3m+2,\\ |E_{\{2,4\}}|&=&2n,\\ |E_{\{4,4\}}|&=&n-1. \end{eqnarray*} Thus, the \(M-polynomial\) of \(CO^{n}_{m}\) is $$ M(CO^{n}_{m};x,y)=(mn-3n+2)x^2y^2+2nx^2y^4+(n-1)x^4y^4.$$
Corollary 10. Let \(CO^{n}_{m}\) be ortho cacti chain of cycles for \(m\ge 3, n\ge 2.\) Then
- \(M_1(CO^{n}_{m})=4mn+8n-8.\)
- \(M_2(CO^{n}_{m})=4mn+20n-24.\)
- \(^{m}M_2(CO^{n}_{m})= \frac{4mn-7n+7}{16}.\)
- \(S_{D}(CO^{n}_{m})= 2mn+n.\)
- \(H(CO^{n}_{m})=\frac{6mn-7n+9}{12}.\)
- \(I_{n}(CO^{n}_{m})= \frac{3mn+5n}{3}.\)
- \(\chi_{\alpha}(CO^{n}_{m})=(mn-3n+2)4^{\alpha}+2n6^{\alpha}+(n-1)8^\alpha.\)
- \(M^{\alpha}_{1}(CO^{n}_{m})=(mn-3n+2)2^{\alpha}+(n-1)2^{2\alpha-1}+n2^{\alpha}(2^{\alpha-1}+1).\)
- \(R_{\alpha}(CO^{n}_{m})=(mn-3n+2)2^{2\alpha}+n2^{3\alpha+1}+(n-1)4^{2\alpha}.\)
Proof. Using the Theorem 9 and column 4 of Table 1, we get the desired results.
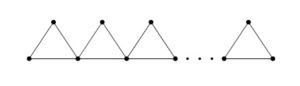
Now, we consider chain triangular cactus as shown in Figure 3, denoted by \(T_{n}\), where \(n\) is the length of the \(T_{n}\). \(T_{n}\) is special case of \(CO^{n}_{m}\) for \(m=3.\)Figure 3. Chain triangular Cactus \(T_{n}.\)
Corollary 11. Let \(T_{n}\) be the chain triangular cactus for \(n\ge 2\). Then \begin{eqnarray*} M(T_{n};x,y)&=&2x^2y^2+2nx^2y^4+(n-1)x^4y^4. \end{eqnarray*}
Proof. The proof follows by substituting \(m=3\) in Theorem 9.
Corollary 12. Let \(T_{n}\) be the chain triangular cactus for \(n\ge 2\). Then
- \(M_1(T_{n})=20n-8.\)
- \(M_2(T_{n})=32n-24.\)
- \(^{m}M_2(T_{n})= \frac{5n+7}{16}.\)
- \(S_{D}(T_{n})= 7n.\)
- \(H(T_{n})=\frac{11n+9}{12}.\)
- \(I_{n}(T_{n})= \frac{14n}{3}.\)
- \(\chi_{\alpha}(T_{n})=2^{2\alpha+1}+2n6^{\alpha}+(n-1)8^\alpha.\)
- \(M^{\alpha}_{1}(T_{n})=2^{\alpha+1}+(n-1)2^{2\alpha-1}+n2^{\alpha}(2^{\alpha-1}+1).\)
- \(R_{\alpha}(T_{n})=2^{2\alpha+1}+n2^{3\alpha+1}+(n-1)4^{2\alpha}.\)
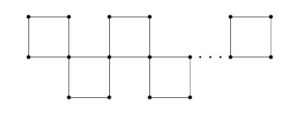
Figure 4. Ortho chain square cactus \(O_{n}.\)
Corollary 13. Let \(O_{n}\) be the ortho-chain square cactus for \(n\ge 2\). Then \begin{eqnarray*} M(O_{n};x,y)&=&(n+2)x^2y^2+2nx^2y^4+(n-1)x^4y^4. \end{eqnarray*}
Proof. The proof follows by substituting \(m=4\) in Theorem 9.
Corollary 14. Let \(O_{n}\) be the ortho-chain square cactus for \(n\ge 2\). Then
- \(M_1(O_{n})=24n-8.\)
- \(M_2(O_{n})=36n-24.\)
- \(^{m}M_2(O_{n})= \frac{9n+7}{16}.\)
- \(S_{D}(O_{n})= 9n.\)
- \(H(O_{n})=\frac{17n+9}{12}.\)
- \(I_{n}(O_{n})= \frac{17n}{3}.\)
- \(\chi_{\alpha}(O_{n})=(n+2)4^{\alpha}+2n6^{\alpha}+(n-1)8^{\alpha}.\)
- \(M^{\alpha}_{1}(O_{n})=(n+2)2^{\alpha}+(n-1)2^{2\alpha-1}+n2^{\alpha}(2^{\alpha-1}+1).\)
- \(R_{\alpha}(O_{n})=(n+2)2^{2\alpha}+n2^{3\alpha+1}+(n-1)4^{2\alpha}.\)
Figure 6. An example of \(Q(m,n)\) graph
Theorem 15. Let \(Q(m,n)\) be ortho-chain for \(m, n\ge 2.\) Then \begin{eqnarray*} M(Q(m,n);x,y)&=&\frac{m(n-1)(n-2)}{2}x^{n-1}y^{n-1}+m(n-1)x^{n-1}y^{m+n-2}+ \frac{m(n-1)}{2}x^{m+n-2}y^{m+n-2}. \end{eqnarray*}
Proof. The edge partition of \(Q(m,n)\) is partitioned into the following subsets, \begin{eqnarray*} E_{1}&=&{\{uv\in E(Q(m,n)): d_{Q(m,n)}(u)=d_{Q(m,n)}(v)=(n-1)\}},\\ E_{2}&=&{\{uv\in E(Q(m,n)): d_{Q(m,n)}(u)=(n-1) \;\; and \;\; d_{Q(m,n)}(v)=(m+n-2)\}},\\ E_{3}&=&{\{uv\in E(Q(m,n)): d_{Q(m,n)}(u)=d_{Q(m,n)}(v)=(m+n-2)\}},\\ \text{Now,}\;\; |E_{1}|&=&\frac{m(n-1)(n-2)}{2},\\ |E_{2}|&=&m(n-1),\\ |E_{3}|&=&\frac{m(n-1)}{2}. \end{eqnarray*} Thus, the \(M-polynomial\) of \(Q(m,n)\) is $$M(Q(m,n);x,y)=\frac{m(n-1)(n-2)}{2}x^{n-1}y^{n-1}+m(n-1)x^{n-1}y^{m+n-2}+ \frac{m(n-1)}{2}x^{m+n-2}y^{m+n-2}.$$
In the para-cacti chain \(C^{n}_{m}\), if we join a new vertex and each cycle of length \(m \ge 3\), \((C_{m}+K_{1})\) then we call it as wheel chain, denoted by \(W^{n}_{m}.\) The number of vertices and edges of \(W^{n}_{m}\) are \(mn+1\) and \(2mn\), respectively. In the following theorem we calculate the \(M-\)polynomial of \(W^{n}_{m}.\)Theorem 16. Let \(W^{n}_{m}\) be wheel chain for \(m \ge 3, n\ge 2.\) Then \begin{eqnarray*} M(W^{n}_{m};x,y)&=&2(m(n-1)-3n+4)x^{3}y^{3}+4(n-1)x^{3}y^{6}+2(m-1)x^{3}y^{m}+2(n-1)x^{6}y^{m}. \end{eqnarray*}
Proof. The edge partition of \(W^{n}_{m}\) is partitioned into the following subsets, \begin{eqnarray*} E_{1}&=&{\{uv\in E(W^{n}_{m}): d_{W^{n}_{m}}(u)=d_{W^{n}_{m}}(v)=3\}},\\ E_{2}&=&{\{uv\in E(W^{n}_{m}): d_{W^{n}_{m}}(u)=3 \;\; and \;\; d_{W^{n}_{m}}(v)=6\}},\\ E_{3}&=&{\{uv\in E(W^{n}_{m}): d_{W^{n}_{m}}(u)=3 \;\; and \;\; d_{W^{n}_{m}}(v)=m\}},\\ E_{4}&=&{\{uv\in E(W^{n}_{m}): d_{W^{n}_{m}}(u)=6 \;\; and \;\; d_{W^{n}_{m}}(v)=m\}},\\ \text{Now,}\;\; |E_{1}|&=&mn-4n+4,\\ |E_{2}|&=&4(n-1),\\ |E_{3}|&=&mn-2n+2,\\ |E_{4}|&=&2(n-1). \end{eqnarray*} Thus, the \(M-polynomial\) of \(W^{n}_{m}\) is $$M(W^{n}_{m};x,y)=(mn-4n+4)x^{3}y^{3}+4(n-1)x^{3}y^{6}+(mn-2n+2)x^{3}y^{m}+2(n-1)x^{6}y^{m}.$$
Figure 6. Wheel chain graph \(W^{n}_{4}.\)
Corollary 17. Let \(W^{n}_{4}\) be the wheel chain graph for \(n\ge 2\). Then \begin{eqnarray*} M(W^{n}_{4};x,y)&=&4x^{3}y^{3}+4(n-1)x^{3}y^{6}+2(n+1)x^{3}y^{4}+2(n-1)x^{6}y^{4}. \end{eqnarray*}
Using Theorem 16 and Tables 1, 2 and 3 one can easily obtain topological indices of wheel chain graph \(W^{n}_{4}\). Since it is a routine task, we omit the calculation here.3. Conclusion
In this paper, we have obtained \(M-\)polynomials of some cactus graphs. We have shown that the general Zagreb index can also be derived from the \(M-\)polynomial of a graph. As an example, we have derived general Zagreb index of cactus graphs from the \(M-\) polynomial of cactus graphs. The Theorem 1 obtained in [9] is the same as the corollary 3 proved in this paper. Thus generalising the results of general Zagreb index of some cactus graphs.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest:
The authors declare no conflict of interest.References
- Basavanagoud, B., & Chitra, E. (2018). On leap Zagreb indices of generalized xyz-point-line transformation graphs \(T^{xyz}(G)\) when \(z=1\). Mathematical Combinatorics, 2, 44-66. [Google Scholor]
- Basavanagoud, B., & Chitra, E. (2018). On leap Zagreb indices of some nanostructures. Malaya Journal of Matematik, 6(4), 816-822.
- Basavanagoud, B., & Chitra, E. (2018). On leap hyper-Zagreb indices of some nanostructures. International Journal of Mathematics Trends and Technology, 64(1), 30 -36.
- Basavanagoud, B., & Jakkannavar, P. (2019). Kulli-Basava Indices of Graphs. International Journal of Applied Engineering Research, 14(1), 325-342. [Google Scholor]
- Gao, W., Wang, W., Dimitrov, D., & Wang, Y. (2018). Nano properties analysis via fourth multiplicative ABC indicator calculating. Arabian journal of chemistry, 11(6), 793-801.[Google Scholor]
- Gao, W., Iqbal, Z., Ishaq, M., Aslam, A., & Sarfraz, R. (2019). Topological aspects of dendrimers via distance based descriptors. IEEE Access, 7, 35619-35630.[Google Scholor]
- Gutman, I. (2013). Degree-based topological indices. Croatica Chemica Acta, 86(4), 351-361.[Google Scholor]
- Li, X., & Shi, Y. (2008). A survey on the Rendić index. MATCH - Communications in Mathematical and in Computer Chemistry, 59(1), 127-156. [Google Scholor]
- De, N. (2019). General Zagreb index of some cactus chains. Open Journal of Discrete Applied Mathematics, 2(1), 24-31. [Google Scholor]
- Sadeghieh, A., Alikhani, S., Ghanbari, N., & Khalaf, A. J. M. (2017). Hosoya polynomial of some cactus chains. Cogent Mathematics & Statistics, 4(1), 1305638.[Google Scholor]
- Sadeghieh, A., Ghanbari, N., & Alikhani, S. (2018). Computation of Gutman index of some cactus chains. Electronic Journal of Graph Theory and Applications, 6(1), 138-151. [Google Scholor]
- West, D. B. (1996). An Introduction to Graph Theory. Prentice-Hall: Upper Saddle River, NJ, USA. [Google Scholor]
- Deutsch, E., & Klav\(\check{\text{z}}\)ar, S. (2015). M-Polynomial and degree-based topological indices. Iranian Journal of Mathematical Chemistry, 6(2), 93-102. [Google Scholor]
- Gutman, I. (2002). Molecular graphs with minimal and maximal Rendić indices. Croatica chemica acta, 75(2), 357-369. [Google Scholor]
- Deutsch, E., & Klav\(\check{\text{z}}\)ar, S. (2019). M-Polynomial Revisited: Bethe Cacti and an Extension of Gutman's Approach. arXiv:1806.08183v2. [Google Scholor]
- Munir, M., Nazeer, W., Rafique, S., & Kang, S. (2016). M-polynomial and related topological indices of Nanostar dendrimers. Symmetry, 8(9), 97. [Google Scholor]
- Munir, M., Nazeer, W., Nizami, A., Rafique, S., & Kang, S. (2016). M-polynomials and topological indices of titania nanotubes. Symmetry, 8(11), 117.[Google Scholor]
- Munir, M., Nazeer, W., Rafique, S., & Kang, S. (2016). M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry, 8(12), 149. [Google Scholor]
- Basavanagoud, B., & Jakkannavar, P. M-Polynomial and degree-based topological indices. Electronic Journal of Mathematical analysis and Applications. (Accepted).[Google Scholor]
- Basavanagoud, B., Anand, P. B., & Praveen, J. M-Polynomial and degree-based topological indices. Submitted for publication.
- Li, X., & Zhao, H. (2004). Trees with the first three smallest and largest generalized topological indices. MATCH - Communications in Mathematical and in Computer Chemistry, 50, 57-62. [Google Scholor]
- Azari, M., & Iranmanesh, A. (2011). Generalized Zagreb index of graphs. Studia Universitatis Babes-Bolyai, Chemia, 56(3), 59-70. [Google Scholor]