Degree tolerant number of power graph: finite Albenian group

1. Introduction

Since, the foundation paper titled, Degree Tolerant Coloring of Graphs is under review, sufficient results and concepts will be recalled to makes this paper digestible. It is assumed that the reader is familiar with the definition and properties of finite Albenian groups over the operation addition \(+\), (or, multiplication \(\times\)). For ease of reference we recall that, depending on the characteristics of the elements of a non-empty set \(X\), the operations \(+\) or \(\times\) can be abstract operations. Having said that, we recall that if \(X\) is a non-empty set and \(f\) is a binary operation on \(X\) i.e., \(f:X\times X\rightarrow X\) we can denote, \(f((a,b))=a\circ b\). The ordered pair \((X,f)\) is a group if:

• (i) \(f\) is associative i.e. \(a\circ(b\circ c)=(a\circ b)\circ c\), \(\forall a,b,c\in X\).
• (ii) A \(e\in X\) exists such that, \(a\circ e=a\), \(\forall a\in X\) (called a right identity of \((X,f)\)).
• (iii) A \(b \in X\) exists for each \(a\in X\) such that, \(a\circ b=e\) (called a right inverse of \(a\)).

If for all \(a,b \in X\) we have \(a\circ b=b\circ a\) then \((X,f)\) is an Albenian group (also called a commutative group). A good introduction is found amongst others, in [1]. In this paper we will consider only a specific finite Albenian group.

It is also assumed that the reader is familiar with most of the classical concepts in graph theory. Throughout only finite, connected simple graphs will be considered. For more on general notation and concepts in graphs see [2,3,4]. It is also assumed that the reader is familiar with the concept of graph coloring. In a proper coloring of \(G\) all edges are said to be good i.e. \(\forall~uv \in E(G)\), \(c(u)\neq c(v)\). The set of colors assigned in a graph coloring is denoted by \(\mathcal{C}\) and a subset of colors assigned to a subset of vertices \(X\subseteq V(G)\) is denoted by \(c(X)\). In an improper (or defect) coloring it is permitted that for some \(uv \in E(G)\), the coloring is \(c(u)=c(v)\).

Recall that for a degree tolerant coloring abbreviated as, \(DT\)-coloring of a graph \(G\) the following condition is set:

• (i) If \(uv \in E(G)\) and \(deg(u)=deg(v)\) then, \(c(u)=c(v)\) else, \(c(u)\neq c(v)\).

Alternative formulation for condition (i). If \(uv \in E(G)\) then, \(c(u)=c(v)\) if and only if \(deg(u)=deg(v)\). The minimum number of colors which yields a \(DT\)-coloring is called the degree tolerant chromatic number of \(G\) and is denoted by, \(\chi_{dt}(G)\). A salient condition which is implied is, if \(uv \notin E(G)\) then, either \(c(u)=c(v)\) or \(c(u)\neq c(v)\). For \(K_n\), \(n\geq 1\) it easily follows that, \(\chi_{dt}(K_n) =1 \leq \chi(K_n)\). In fact, for \(n\geq 2\) it follows that, \(\chi_{dt}(K_n) < \chi(K_n)\). Furthermore, for paths \(P_1\), \(P_2\) we find \(\chi_{dt}(P_1) = \chi_{dt}(P_2) =1\). On the other hand for \(n \geq 3\) we have, \(\chi_{dt}(P_n) = \chi(P_n) = 2\). In the aforesaid it is only the coloring assignment which differs.

Consider the set \(R_u= \{deg(v): v\in N[u], u\in V(G)\}\). The degree tolerant index of \(u \in V(G)\) is defined by \(\rho(u) = |R_u|\). Note that since repetition in a set is not permitted, \(\rho(u) \leq |N[u]|\). Let the degree tolerant index of a graph \(G\) be \(\rho(G) = \max\{\rho(u):\) over all \(u\in V(G)\}\). We recall a result of interest.

Theorem 1. For a graph \(G\), it follows that \(\chi_{dt}(G)\leq \rho(G)\).

2. Albenian group \(\mathbb{Z}_n\) under addition modulo \(n\): \(n\in \mathbb{N}\)

Denote the finite Albenian group \(\mathbb{Z}_n\) under addition modulo \(n\), \(n\in \mathbb{N}\) by, \((\mathbb{Z}_{n},+_{n})\). We have \(\mathbb{Z}_n=\{0,1,2,\dots,n-1\}\) and the generator set, \(\mathbb{Z}_{gen}=\{m:m\) relatively prime to \(n\}\). Let \(\mathbb{P} =\{\)prime numbers\(\}\).

Since it is known that that any non-prime positive integer \(n\geq 4\) can be written as a product of prime numbers, begin by considering a product of two distinct primes i.e. \(n=p_1p_2\), \(p_1,p_2 \in \mathbb{P}\). It is agreed that the terms prime and prime number may be used interchangeably.

Lemma 1. For distinct positive integers \(m_1,m_2\), there are exactly \(m_1-1\) multiples of \(m_2\) and exactly \(m_2-1\) multiples of \(m_1\) in the integer range \([0,m_1m_2-1]\).

Proof. The number of multiples of \(m_1\) and \(m_2\) in the integer range \([0,m_1m_2-1]\) is given by \(\lfloor \frac{m_1p_m-1}{p_1}\rfloor\) and \(\lfloor \frac{m_1m_2-1}{m_2}\rfloor\) respectively. Further through simplification $$\lfloor \frac{m_1m_2-1}{m_1}\rfloor =m_2-1$$ and $$\lfloor \frac{m_1m_2-1}{m_2}\rfloor = m_1-1$$.

The respective sets of multiples of the primes \(p_1\) and \(p_2\) in the integer range \([0,p_1p_2-1]\) are denoted by \(M_{p_1}\) and \(M_{p_2}\). The vertex set of the power graph denoted by \(\mathcal{P}((\mathbb{Z}_{n},+_{n}))\) is \(V(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) = \{v_0,v_1,v_2,\dots,v_{p_1p_2-1}\}\). Alternatively, \(V_{\mathcal{P}}(\mathbb{Z}_n)\) (for brevity). The power graph has edge set \(E(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) = \{v_iv_j: i\in \mathbb{Z}_{gen}\cup \{0\}, v_j \in V_{\mathcal{P}}(\mathbb{Z}_n), i\neq j\} \cup \{v_kv_\ell: k,\ell \in M_{p_1}, k \neq \ell\} \cup \{v_mv_\tau: m,\tau \in M_{p_2}, m \neq \tau\} = E_{\mathcal{P}}(\mathbb{Z}_n)\), (for brevity).

Remark 1. Conventionally the power graph is a directed graph. We only consider the undirected case, hence the underlying power graph.

Note that a result stemming from the Euler \(\varphi\)-function (see Theorem 2.13.5, [1]) yields \(|\mathbb{Z}_{gen}|=(p_1-1)(p_2-1)\). Since \(|V(\mathcal{P}((\mathbb{Z}_{n},+_{n})))| = p_1p_2\), the above implies that the vertex set of the power graph \(\mathcal{P}((\mathbb{Z}_{n},+_{n}))\) can be partitioned into:

\(|V_1|= (p_2-1)\)-set and \(deg (v_i)=p_1(p_2-1)\), \(v_i\in V_1\),

\(|V_2|= (p_1-1)\)-set and \(deg(v_j)= p_2(p_1-1)\), \(v_j\in V_2\),

\(|V_{gen}\cup \{v_0\}| = (p_1p_2 -p_1-p_2+2)\)-set and \(deg(v_k)= p_1p_2-1\), \(v_k \in V_{gen}\cup \{v_0\}\).

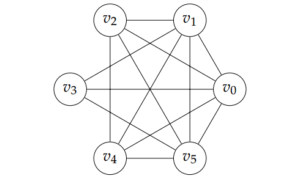
The Figure 1 depicts \(\mathcal{P}((\mathbb{Z}_{n},+_{n}))\), \(p_1=2\), \(p_2=3\).

2.1. Degree tolerant chromatic number of \((\mathbb{Z}_{n},+_{n})\)

Lemma 2. For a positive integer \(n=p_1p_2\), \(p_1,p_2 \in \mathbb{P}\), \(p_1\neq p_2\), we have that \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) = 2\).

Proof. Since \(\rho(v_i)=2\), \(v_i\in V_1\), \(\rho(v_j)=2\), \(v_j \in V_2\) and \(\rho(v_k)=3\), \(v_k \in V_{gen}\cup \{v_0\}\), it follows that \(\rho(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) = 3\). From Theorem 1, \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) \leq 3\). Since \(V_1\cap V_2=\emptyset\) the coloring \(c(V_1)=c(V_2)\) is permissible in a minimal \(DT\)-coloring. Hence \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) \leq 2\). However \(\mathcal{P}((\mathbb{Z}_{n},+_{n}))\) is not regular, so \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) \geq 2\). This settles the result.

Now consider \(n=p_1p_2p_3\), \(p_1,p_2,p_3 \in \mathbb{P}\) and \(p_i\neq p_j\) for all pairs.

Lemma 3. In the integer range \([0,p_1p_2p_3-1]\), let \(V_1 = \{\)multiples of \(p_1\}\), \(V_2 = \{\)multiples of \(p_2\}\), \(V_3= \{\)multiples of \(p_3\}\). Then \(|V_1 \cap V_2|=p_3-1\), \(|V_1\cap V_3|=p_2-1\) and \(|V_2\cap V_3|=p_1-1\).

Proof. Noting that without loss of generality \(V_i\cap V_j=\lfloor \frac{1}{p_i}\cdot\lfloor \frac{p_ip_jp_k -1}{p_j}\rfloor \rfloor = p_k-1\), the result follows.

Lemma 4. For a positive integer \(n=p_1p_2p_3\) and \(p_1,p_2,p_3 \in \mathbb{P}\), we have \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) = 3\).

Proof. Similar to the vertex partition for the case \(n=p_1p_2\), the vertex set \(V(\mathcal{P}((\mathbb{Z}_{n},+_{n})))\) for the case \(n=p_1p_2p_3\) can be partitioned into \(V_1\), \(V_2\),\(V_3\) and \(V_{gen}\cup \{v_0\}\). Clearly, by similar reasoning found in the proof of Lemma 3, \(\chi_{dt}((\mathbb{Z}_{n},+_{n})) \leq 4\). Since no multiple of \(p_1p_2p_3\) exists, it follows that no induced \(K_3\) exists on a triple \(v_i,v_j,v_k\), \(v_i \in V_1\), \(v_j\in V_2\), \(v_k\in V_3\). Therefore \(\chi_{dt}((\mathbb{Z}_{n},+_{n})) \leq 3\).

Since \(p_i,p_j,p_k\geq 2\), it follows that \(V_i \cap V_j \neq \emptyset\). Therefore, an induced \(K_3\) exists in \(\mathcal{P}((\mathbb{Z}_{n},+_{n}))\) such that each vertex has degree distinct from the other. Note that one of the vertices will be in \(V_{gen}\cup \{v_0\}\). By condition (ii), \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n})))\geq 3\). Hence the result.

We are ready to present the main result.

Theorem 2. For a positive integer \(n= \prod\limits_{i=1}^{k}p_i\), \(p_i\in \mathbb{P}\) and \(p_i \neq p_j\) iff \(i\neq j\), we have \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) = k\).

Proof. The result follows by Lemmas 1,2,3,4 and the utilization of induction.

3. Conclusion

It is known that for some graphs \(\chi_{dt}(G)< \chi(G)\).

Problem 1. Show that for a positive integer \(n= \prod\limits_{i=1}^{k}p_i\), \(p_i\in \mathbb{P}\) and \(p_i \neq p_j\) iff \(i\neq j\) that \(\chi_{dt}(\mathcal{P}((\mathbb{Z}_{n},+_{n}))) < \chi(\mathcal{P}((\mathbb{Z}_{n},+_{n})))\).

The numerous finite Albenian groups offer a wide scope for further research.

Acknowledgments

The author would like to thank the anonymous referees for their constructive comments, which helped to improve on the elegance of this short paper.

Conflict of Interests

''The author declares no conflict of interest.''