Open Journal of Chemistry
ISSN: 2618-0758 (Online) 2618-074X (Print)
DOI: 10.30538/psrp-ojc2018.0005
Some Algebraic Polynomials and Topological Indices of Möbius Ladder
Muhammad Asif Tahir\(^1\), Saba Noreen
Department of Mathematics, The University of Lahore (Pakpattan Campus), Lahore Pakistan.; (M.A.T)
Department of Mathematics and Statistics, The University of Lahore, Lahore Pakistan.; (S.N)
\(^{1}\)Corresponding Author; asiftahir46@gmail.com
Abstract
Keywords:
A graph \(G\) is an ordered pair \((V,E)\), where \(V\) is the set of vertices and \(E\) is the set of edges. A path from a vertex \(v\) to a vertex \(w\) is a sequence of vertices and edges that starts from \(v\) and stops at \(w\). The number of edges in a path is called the length of that path. A graph is said to be connected if there is a path between any two of its vertices. The distance \(d(u,v)\) between two vertices \(u\), \(v\) of a connected graph \(G\) is the length of a shortest path between them. Graph theory is contributing a lion's share in many areas such as chemistry, physics, pharmacy, as well as in industry [10]. We will start with some preliminary facts.
The first and the second Zagreb indices are defined as \begin{equation*} M_{1}(G)=\sum\limits_{u\in V(G)}(d_{u}+d_{v}), \end{equation*} \begin{equation*} M_{2}(G)=\sum\limits_{uv\in E(G)}d_{u}\times d_{u}, \end{equation*} \noindent For details see [11]. Considering the Zagreb indices, Fath-Tabar ([12]) defined first and the second Zagreb polynomials as $$M_{1}(G,x)=\sum\limits_{uv\in E(G)}x^{d_{u}+d_{v}},$$ and $$M_{2}(G,x)=\sum\limits_{uv\in E(G)}x^{d_{u}.d_{v}}.$$ The properties of \(M_{1}(G,x)\) , \(M_{2}(G,x)\) polynomials for some chemical structures have been studied in the literature [13, 14].
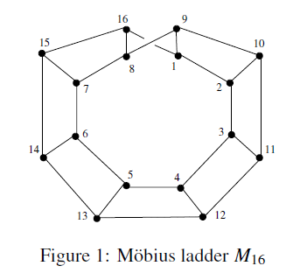
After that, in [15], the authors defined the third Zagreb index $$M_{3}(G)=\sum\limits_{uv\in E(G)}(d_{u}-d_{v}),$$ and the polynomial $$M_{3}(G,x)=\sum\limits_{uv\in E(G)}x^{d_{u}-d_{v}}.$$ In the year 2016, [16] following Zagreb type polynomials were defined $$M_{4}(G,x)=\sum\limits_{uv\in E(G)}x^{d_{u}(d_{u}+d_{v})},$$ $$M_{5}(G,x)=\sum\limits_{uv\in E(G)}x^{d_{v}(d_{u}+d_{v})},$$ $$M_{a,b}(G,x)=\sum\limits_{uv\in E(G)}x^{ad_{u}+bd_{v}},$$ $$M'_{a,b}(G,x)=\sum\limits_{uv\in E(G)}x^{(d_{u}+a)(d_{v}+b)}.$$ Ranjini et al. [17] redefines the Zagreb index, ie, the redefined first, second and third Zagreb indices of graph \(G\). These indicators appear as $$Re ZG_{1}(G)=\sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{d_{u}d_{v}},$$ $$Re ZG_{2}(G)=\sum\limits_{uv\in E(G)}\frac{d_{u}.d_{v}}{d_{u}+d_{v}},$$ and $$Re ZG_{3}(G)=\sum\limits_{uv\in E(G)}(d_{u}+d_{v})(d_{u}.d_{v}).$$ In this paper we compute other Zagreb polynomials and Redefined Zagreb indices of Möbiusbius Ladder. The Möbius ladder \(M_{n}\) which is a cubic circulant graph with an even number of vertices, formed from an n-cycle by adding edges (called "rungs") connecting opposite pair of vertices in the cycle. It is so-named because (with the exception of \(M_{6}=K_{3,3}\) has exactly \(\frac{n}{2}\) \(4\)-cycles which link together by their shared edges to form a topological Möbius strip. Möbius ladders can also be viewed as a prism with one twisted edge. Two different views of Möbius ladders have been shown in Figure 1. Möbius ladders have many applications in chemistry, chemical stereography, electronics and computer science. For our convenience, we view the Möbius ladder \(M_{n}\) which is a cubic circulant graph with an even number of vertices, formed from an n-cycle by adding edges (called "rungs") connecting opposite pair of vertices in the cycle.
2. Computational Results
Let In this section, we present our computational results.Theorem 2.1 Let \(M_{n}\) be the Möbius Ladder. Then
- \(M_{3}(M_{n},x)=3n,\)
- \(M_{4}(M_{n},x)=3nx^{18},\)
- \(M_{5}(M_{n},x)=3nx^{18},\)
- \(M_{a,b}(M_{n},x)=3nx^{3a+3b},\)
- \(M'_{M_{n},b}(G,x)=3nx^{(3+a)(3+b)}.\)
Proof.
Let \(M_{n}\) be the Möbius Ladder. It is clear that \(M_{n}\) has only one partition of vertex set i.e,
$$V_{1}=\{v\in V(M_{n}): d_{v}=3\},$$
The edge set of \(M_{n}\) has following one partition,
$$E_{1}=E_{3,3}=\{e=uv\in E(M_{n}): d_{u}=3, d_{v}=3\},$$
Now,
$$\mid E_{1}(M_{n})\mid=3n,$$
Theorem 2.2 Let \(M_{n}\) be the Möbius Ladder. Then,
- \(Re ZG_{1}(M_{n})=2n\),
- \(Re ZG_{2}(M_{n})= \frac{9}{2}n\),
- \(Re ZG_{3}(M_{n})=162n\).
Proof.
-
(1) \begin{eqnarray*}
Re ZG_{1}(M_{n})&=&\sum\limits_{uv\in E(M_{n})}\frac{d_{u}+d_{v}}{d_{u}d_{v}}\\
&=&\sum\limits_{uv\in E_{1}(M_{n})}\frac{d_{u}+d_{v}}{d_{u}d_{v}}\\
&=&\sum\limits_{uv\in E_{1}(M_{n})}\frac{3+3}{3.3}\\
&=&\mid E_{1}(M_{n})\mid \frac{6}{9}\\
&=&(3n)\frac{6}{9}\\
&=& 2np.
\end{eqnarray*}
(2) \begin{eqnarray*}
Re ZG_{2}(G)&=&\sum\limits_{uv\in E(M_{n})}\frac{d_{u}.d_{v}}{d_{u}+d_{v}}\\
&=&\sum\limits_{uv\in E_{1}(M_{n})}\frac{d_{u}.d_{v}}{d_{u}+d_{v}}\\
&=&\sum\limits_{uv\in E_{1}(M_{n})}\frac{3.3}{3+3}\\
&=&(3n)\frac{3}{2}\\
&=& \frac{9}{2}n.
\end{eqnarray*}
(3) \begin{eqnarray*}
Re ZG_{2}(G)&=&\sum\limits_{uv\in E(M_{n})}(d_{u}.d_{v})(d_{u}+d_{v})\\
&=&\sum\limits_{uv\in E_{1}(M_{n})}(d_{u}.d_{v})(d_{u}+d_{v})\\
&=&\sum\limits_{uv\in E_{1}(M_{n})}(3.3)(3+3)\\
&=&\mid E_{1}(G)\mid 54\\
&=&3n(54)\\
&=& 162n.
\end{eqnarray*}
Competing Interests
The authors declare that they have no competing interests.References
- Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20. [Google Scholor]
- Katritzky, A. R., Jain, R., Lomaka, A., Petrukhin, R., Maran, U., & Karelson, M. (2001). Perspective on the relationship between melting points and chemical structure. Crystal Growth & Design, 1(4), 261-265. [Google Scholor]
- Rücker, G., & Rücker, C. (1999). On topological indices, boiling points, and cycloalkanes. Journal of chemical information and computer sciences, 39(5), 788-802. [Google Scholor]
- Dobrynin, A. A., Entringer, R., & Gutman, I. (2001). Wiener index of trees: theory and applications. Acta Applicandae Mathematica , 66(3), 211-249. [Google Scholor]
- Du, W., Li, X., & Shi, Y. (2009). Algorithms and extremal problem on Wiener polarity index. MATCH Commun. Math. Comput. Chem, 62(1), 235. [Google Scholor]
- Gutman, I., & Polansky, O. E. (2012). Mathematical concepts in organic chemistry. Springer Science & Business Media. [Google Scholor]
- Ma, J., Shi, Y., & Yue, J. (2014). The Wiener Polarity Index of Graph Products. Ars Comb., 116, 235-244. [Google Scholor]
- Ma, J., Shi, Y., Wang, Z., & Yue, J. (2016). On Wiener polarity index of bicyclic networks. Scientific reports, 6, 19066. [Google Scholor]
- Gutman, I. (1993). Some properties of the Wiener polynomial. Graph Theory Notes New York , 125, 13-18. [Google Scholor]
- Deutsch, E., & Klavžar, S. (2015). M-polynomial and degree-based topological indices. Iran. J. Math. Chem., (6) 93–102. [Google Scholor]
- Gutman, I., & Trinajstić, N. (1972). Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17(4), 535-538. [Google Scholor]
- Fath-Tabar, G. H. (2011). Old and new Zagreb indices of graphs. MATCH Commun. Math. Comput. Chem, 65(1), 79-84. [Google Scholor]
- Gutman, I., & Das, K. C. (2004). The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem, 50(1), 83-92. [Google Scholor]
- Ranjini, P. S., Lokesha, V., Bindusree, A. R., & Raju, M. P. (2012). New bounds on Zagreb indices and the Zagreb co-indices. Boletim da Sociedade Paranaense de Matemática, 31(1), 51-55. [Google Scholor]
- Fath-Tabar, G. (2009). Zagreb polynomial and pi indices of some nano structures. Digest Journal of Nanomaterials & Biostructures (DJNB), 4(1), 189-191. [Google Scholor]
- Bindusree, A. R., Cangul, I. N., Lokesha, V., & Cevik, A. S. (2016). Zagreb polynomials of three graph operators. Filomat, 30(7), 1979-1986. [Google Scholor]
- Ranjini, P. S., Lokesha, V., & Usha, A. (2013). Relation between phenylene and hexagonal squeeze using harmonic index. International Journal of Graph Theory, 1(4), 116-121. [Google Scholor]