Open Journal of Mathematical Analysis
ISSN: 2616-8111 (Online) 2616-8103 (Print)
DOI: 10.30538/psrp-oma2019.0032
Solutions structures for some systems of fractional difference equations
Department of Mathematics, Faculty of Science, Taibah University, P.O. Box 30002, Saudi Arabia.; (M.B.A)
\(^{1}\)Corresponding Author: mmutrafi@taibahu.edu.sa
Abstract
$$
x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left( -1-x_{n-1}y_{n-3}\right) },\ \ \
y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left( \pm 1\pm y_{n-1}x_{n-3}\right) }
,\ \ \ n=0,1,…,
$$
where the initial data \(x_{-3},\ x_{-2},\ x_{-1},\ \)\ \(
x_{0},\ y_{-3},\ y_{-2},\ y_{-1}\) and \(\ \ y_{0}\;\) are arbitrary non-zero real numbers. All solutions will be depicted under specific initial conditions.
Keywords:
1. Introduction
he theory of discrete dynamical systems of difference equations has been utilized to study natural phenomena which change over discrete time. A massive number of researchers investigated various real life problems that occur in population dynamics, genetics in biology, engineering, queuing problems, electrical networks, physics, economics, etc [1]. The long-term behaviours of such problems have been recently discussed by some scholars. For example, in [2] Asiri et al. explained the periodic solutions of the following system of difference equations: \begin{equation*} x_{n+1}=\frac{y_{n-2}}{1-y_{n-2}x_{n-1}y_{n}},\ \ \ y_{n+1}=\frac{x_{n-2}}{ \pm 1\pm x_{n-2}y_{n-1}x_{n}}. \end{equation*} Cinar [3] explored the periodicity of non-negative solutions of a system of fractional difference equations given by the form: \begin{equation*} x_{n+1}=\frac{1}{y_{n}},\ \ \ y_{n+1}=\frac{y_{n}}{x_{n-1}y_{n-1}}. \end{equation*} Din [4] analyzed and obtained the equilibrium points, local asymptotic stability and global behaviour of the fixed points of Lotka-Volterra model which is illustrated by the system: \begin{equation*} x_{n+1}=\frac{\alpha x_{n}-\beta x_{n}y_{n}}{1+\gamma x_{n}},\ \ \ y_{n+1}= \frac{\delta y_{n}+\epsilon x_{n}y_{n}}{1+\eta y_{n}}. \end{equation*} El-Metwally et al. [5] found the solutions and the periodicity of the following third order system of rational recursive equations: \begin{equation*} x_{n+1}=\frac{y_{n-2}}{-1-y_{n-2}x_{n-1}y_{n}},\ \ \ y_{n+1}=\frac{x_{n-2}}{ \pm 1\pm x_{n-2}y_{n-1}x_{n}}. \end{equation*} In [6], Elsayed presented the solutions of the following system of second order difference equations: \begin{equation*} x_{n+1}=\frac{x_{n-1}}{\pm 1\pm x_{n-1}y_{n}},\ \ \ y_{n+1}=\frac{y_{n-1}}{ \mp 1+y_{n-1}x_{n}}. \end{equation*} Elsayed and Alzubaidi [7] found the solutions of following systems of rational difference equations: \[ x_{n+1}=\frac{y_{n-8}}{1+y_{n-2}x_{n-5}y_{n-8}},\ \ \ \ \ y_{n+1} =\frac{x_{n-8}}{\pm1\pm x_{n-2}y_{n-5}x_{n-8}}. \] G\H{u}m\H{u}\c{s} and \H{O}calan [8] explored the positive solutions of the systems: \[ u_{n+1}=\frac{\alpha u_{n-1}}{\beta+\gamma v_{n}^{p}v_{n-2}^{q}} ,\ \ \ v_{n+1}=\frac{\alpha_{1}v_{n-1}}{\beta_{1}+\gamma_{1}u_{n}^{p_{1} }u_{n-2}^{q_{1}}}. \] Kurbanli et al. [9] obtained the solutions of the following system of difference equations: \begin{equation*} x_{n+1}=\frac{x_{n-1}}{y_{n}x_{n-1}-1},\ \ y_{n+1}=\frac{y_{n-1}}{ x_{n}y_{n-1}-1},\ \ z_{n+1}=\frac{x_{n}}{y_{n}z_{n-1}}. \end{equation*} In [10], Touafek et al. discovered the periodicity and solution of the system: \begin{equation*} x_{n+1}=\frac{x_{n-3}}{\pm 1\pm x_{n-3}y_{n-1}},\ \ \ y_{n+1}=\frac{y_{n-3}}{ \pm 1\pm y_{n-3}x_{n-1}}. \end{equation*} The author in [11] examined the dynamics of the following system of recursive equations: \begin{equation*} x_{n+1}=\frac{x_{n-2}}{B+y_{n}y_{n-1}y_{n-2}},\ \ \ y_{n+1}=\frac{y_{n-2}}{ A+x_{n}x_{n-1}x_{n-2}}. \end{equation*} For more information about basic theory and qualitative behaviour of dynamical systems of difference equations, one can see references [12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 35, 26, 27].This work aims to present the solutions of discrete dynamical systems of difference equations which are given by \begin{equation*} x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left( -1-x_{n-1}y_{n-3}\right) },\ \ \ y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left( \pm 1\pm y_{n-1}x_{n-3}\right) } ,\ \ \ n=0,1,\ldots, \end{equation*} where the initial values \(x_{-3},\ x_{-2},\ x_{-1},\ \)\ \(x_{0},\ y_{-3},\ y_{-2},\ y_{-1}\) and\(\ \ y_{0}\) are required to be real numbers.
2. Main Results
2.1. First system \(x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left( -1-x_{n-1}y_{n-3}\right) },\ y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left( 1+y_{n-1}x_{n-3}\right) }\)
This subsections is devoted for the solutions of the following system of recursive equations:Theorem Let \(\left\{ x_{n},y_{n}\right\} \) be a solution to system (1) and let \(x_{-3}=a,\ x_{-2}=b,\ x_{-1}=c,\ x_{0}=d,\ y_{-3}=\alpha ,\ y_{-2}=\beta ,\ y_{-1}=\gamma \) and \(y_{0}=\omega .\) Then, for \(n=0,\ 1,\ \ldots\), we have \begin{eqnarray*} x_{4n-3} &=&\frac{\left( -1\right) ^{n}c^{n}\alpha ^{n}\underset{i=0}{ \overset{n-1}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] }{ a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}},\ \ \ x_{4n-2}=\frac{\left( -1\right) ^{n}d^{n}\beta ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i\right) b\omega +1\right] }{b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n}}, \\ x_{4n-1} &=&\frac{c^{n+1}\alpha ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] }{a^{n}\gamma ^{n}},\ \ \ x_{4n}=\frac{ d^{n+1}\beta ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+1\right) b\omega +1\right] }{b^{n}\omega ^{n}}, \end{eqnarray*} and \begin{eqnarray*} y_{4n-3} &=&\frac{a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\underset{i=0}{\overset {n-1}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] },\ \ \ y_{4n-2}= \frac{b^{n}\omega ^{n}}{d^{n}\beta ^{n-1}\underset{i=0}{\overset{n-1}{\Pi }} \left[ \left( 2i+1\right) b\omega +1\right] }, \\ y_{4n-1} &=&\frac{\left( -1\right) ^{n}a^{n}\gamma ^{n+1}\left( c\alpha +1\right) ^{n}}{c^{n}\alpha ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+2\right) a\gamma +1\right] },\ \ \ y_{4n}=\frac{\left( -1\right) ^{n}b^{n}\omega ^{n+1}\left( d\beta +1\right) ^{n}}{d^{n}\beta ^{n}\underset{ i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+2\right) b\omega +1\right] }. \end{eqnarray*}
Proof. It is easy to see that the results hold for \(n=0\). Next, we assume that \(n>1\) and suppose that the solutions hold for \(n-1.\) That is \begin{eqnarray*} x_{4n-7} &=&\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] }{ a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}},\ \ \ x_{4n-6}=\frac{ \left( -1\right) ^{n-1}d^{n-1}\beta ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i\right) b\omega +1\right] }{b^{n-2}\omega ^{n-1}\left( d\beta +1\right) ^{n-1}}, \\ x_{4n-5} &=&\frac{c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] }{a^{n-1}\gamma ^{n-1}},\ \ \ x_{4n-4}= \frac{d^{n}\beta ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) b\omega +1\right] }{b^{n-1}\omega ^{n-1}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-7} &=&\frac{a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] },\ \ \ y_{4n-6}=\frac{b^{n-1}\omega ^{n-1}}{d^{n-1}\beta ^{n-2}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+1\right) b\omega +1\right] }, \\ y_{4n-5} &=&\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i+2\right) a\gamma +1\right] },\ \ \ y_{4n-4}=\frac{\left( -1\right) ^{n-1}b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n-1}}{ d^{n-1}\beta ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) b\omega +1\right] }. \end{eqnarray*} Following this, system (1) gives us \begin{eqnarray*} x_{4n-3} &=&\frac{x_{4n-5}y_{4n-7}}{y_{4n-5}\left( -1-x_{4n-5}y_{4n-7}\right) } \\ &=&\frac{\frac{c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] }{a^{n-1}\gamma ^{n-1}}\frac{ a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i+1\right) a\gamma +1\right] }}{\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1} \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma +1 \right] }\left[ -1-\frac{c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi } }\left[ \left( 2i+1\right) a\gamma +1\right] }{a^{n-1}\gamma ^{n-1}}\frac{ a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i+1\right) a\gamma +1\right] }\right] } \\ &=&\frac{-\left( -1\right) ^{-n+1}c^{n}\alpha ^{n}\underset{i=0}{\overset{n-2 }{\Pi }}\left[ \left( 2i+2\right) a\gamma +1\right] }{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}\left[ 1+c\alpha \right] }=\frac{\left( -1\right) ^{n}c^{n}\alpha ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] }{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}}. \end{eqnarray*} Moreover, one can observe from system (1) that \begin{eqnarray*} y_{4n-3} &=&\frac{y_{4n-5}x_{4n-7}}{x_{4n-5}\left[ 1+y_{4n-5}x_{4n-7}\right] } \\ &=&\frac{\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i+2\right) a\gamma +1\right] }\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] }{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}}{\frac{c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] }{a^{n-1}\gamma ^{n-1}}\left[ 1+\frac{ \left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{ c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma +1\right] }\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1 \right] }{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}\right] } \end{eqnarray*} \begin{eqnarray*} &=&\frac{\frac{a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] }{\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma +1\right] }}{\frac{c^{n}\alpha ^{n-1}\underset{i=0 }{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] }{ a^{n-1}\gamma ^{n-1}}\left[ 1+\frac{a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] }{\underset{i=0}{\overset{n-2}{ \Pi }}\left[ \left( 2i+2\right) a\gamma +1\right] }\right] } \\ &=&\frac{a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] a^{n-1}\gamma ^{n-1}}{c^{n}\alpha ^{n-1}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] \left[ \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma +1 \right] +a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma +1\right] \right] } \\ &=&\frac{a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-1}{ \Pi }}\left[ \left( 2i+1\right) a\gamma +1\right] }. \end{eqnarray*} Similarly, other results can be proved. The proof has been completed.
Second System \(x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left(
-1-x_{n-1}y_{n-3}\right) },\ y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left(
-1-y_{n-1}x_{n-3}\right) }\)
In this section, we obtained the solutions of the following system of differential equations:
\begin{equation}
x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left( -1-x_{n-1}y_{n-3}\right) },\ \ \
y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left( -1-y_{n-1}x_{n-3}\right) }.
\label{p6 sys 2}
\end{equation}
(2)
The initial values of system (2) are required to be arbitrary real numbers.
Theorem 2. Let \(\left\{ x_{n},y_{n}\right\} \) be a solution to system (2) and assume that \(x_{-3}=a,\ x_{-2}=b,\ x_{-1}=c,\ x_{0}=d,\ y_{-3}=\alpha ,\ y_{-2}=\beta ,\ y_{-1}=\gamma \) and \(y_{0}=\omega .\) Then, for \(n=0,\ 1,\ ...\) we have \begin{eqnarray*} x_{4n-3} &=&\frac{\left( -1\right) ^{n}c^{n}\alpha ^{n}}{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}},\ \ \ x_{4n-2}=\frac{\left( -1\right) ^{n}d^{n}\beta ^{n}}{b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n}}, \\ x_{4n-1} &=&\frac{\left( -1\right) ^{n}c^{n+1}\alpha ^{n}\left( a\gamma +1\right) ^{n}}{a^{n}\gamma ^{n}},\ \ \ x_{4n}=\frac{\left( -1\right) ^{n}d^{n+1}\beta ^{n}\left( b\omega +1\right) ^{n}}{b^{n}\omega ^{n}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-3} &=&\frac{\left( -1\right) ^{n}a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n}},\ \ \ y_{4n-2}=\frac{\left( -1\right) ^{n}b^{n}\omega ^{n}}{d^{n}\beta ^{n-1}\left( b\omega +1\right) ^{n}}, \\ y_{4n-1} &=&\frac{\left( -1\right) ^{n}a^{n}\gamma ^{n+1}\left( c\alpha +1\right) ^{n}}{c^{n}\alpha ^{n}},\ \ \ y_{4n}=\frac{\left( -1\right) ^{n}b^{n}\omega ^{n+1}\left( d\beta +1\right) ^{n}}{d^{n}\beta ^{n}}. \end{eqnarray*}
Proof. The solutions are verified for \(n=0\). Next, we let \(n>1\) and assume that the results hold for \(n-1.\) That is \begin{eqnarray*} x_{4n-7} &=&\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}}{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}},\ \ \ x_{4n-6}=\frac{\left( -1\right) ^{n-1}d^{n-1}\beta ^{n-1}}{b^{n-2}\omega ^{n-1}\left( d\beta +1\right) ^{n-1} }, \\ x_{4n-5} &=&\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n-1}}{a^{n-1}\gamma ^{n-1}},\ \ \ x_{4n-4}=\frac{\left( -1\right) ^{n-1}d^{n}\beta ^{n-1}\left( b\omega +1\right) ^{n-1}}{ b^{n-1}\omega ^{n-1}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-7} &=&\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\left( a\gamma +1\right) ^{n-1}},\ \ \ y_{4n-6}=\frac{\left( -1\right) ^{n-1}b^{n-1}\omega ^{n-1}}{d^{n-1}\beta ^{n-2}\left( b\omega +1\right) ^{n-1}}, \\ y_{4n-5} &=&\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}},\ \ \ y_{4n-4}=\frac{\left( -1\right) ^{n-1}b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n-1}}{ d^{n-1}\beta ^{n-1}}. \end{eqnarray*} Now, the first relation is given by \begin{eqnarray*} x_{4n-3} &=&\frac{x_{4n-5}y_{4n-7}}{y_{4n-5}\left( -1-x_{4n-5}y_{4n-7}\right) } \\ &=&\frac{\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n-1}}{a^{n-1}\gamma ^{n-1}}\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\left( a\gamma +1\right) ^{n-1}}}{\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}}\left[ -1-\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n-1}}{a^{n-1}\gamma ^{n-1} }\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\left( a\gamma +1\right) ^{n-1}}\right] } \\ &=&\frac{-\left( -1\right) ^{-n+1}c\alpha \ c^{n-1}\alpha ^{n-1}}{ a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}\left[ 1+c\alpha \right] }= \frac{\left( -1\right) ^{n}c^{n}\alpha ^{n}}{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}}. \end{eqnarray*} Similarly, system (2) leads \begin{eqnarray*} y_{4n-3} &=&\frac{y_{4n-5}x_{4n-7}}{x_{4n-5}\left( -1-y_{4n-5}x_{4n-7}\right) } \\ &=&\frac{\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}}\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}}{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}}{\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n-1}}{a^{n-1}\gamma ^{n-1}}\left[ -1-\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1} }\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}}{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}\right] } \\ &=&\frac{-\left( -1\right) ^{-n+1}a\gamma \ a^{n-1}\gamma ^{n-1}}{ c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n-1}\left[ 1+a\gamma \right] }= \frac{\left( -1\right) ^{n}a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\left( a\gamma +1\right) ^{n}}. \end{eqnarray*} Accordingly, the remaining relations of system (2) can be verified. Hence, this achieves the proof.
2.3. Third System \(x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left(
-1-x_{n-1}y_{n-3}\right) },\ y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left(
1-y_{n-1}x_{n-3}\right) }\)
In this subsection, the solutions of the following dynamic discrete system will be formulated:
\begin{equation}
x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left( -1-x_{n-1}y_{n-3}\right) },\ \ \
y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left( 1-y_{n-1}x_{n-3}\right) },
\label{p6 sys 3}
\end{equation}
(3)
where the initial values are required to be arbitrary real numbers.
Theorem 3. Assume that \(\left\{ x_{n},y_{n}\right\} \) is a solution to system (3) and suppose that \(x_{-3}=a,\ x_{-2}=b,\ x_{-1}=c,\ x_{0}=d,\ y_{-3}=\alpha ,\ y_{-2}=\beta ,\ y_{-1}=\gamma \) and \(y_{0}=\omega .\) Then, for \(n=0,\ 1,\ ...\) we have \begin{eqnarray*} x_{4n-3} &=&\frac{c^{n}\alpha ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}},\ \ \ x_{4n-2}=\frac{d^{n}\beta ^{n}\underset{i=0}{\overset{ n-1}{\Pi }}\left[ \left( 2i\right) b\omega -1\right] }{b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n}}, \\ x_{4n-1} &=&\frac{\left( -1\right) ^{n}c^{n+1}\alpha ^{n}\underset{i=0}{ \overset{n-1}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }{ a^{n}\gamma ^{n}},\ \ \ x_{4n}=\frac{\left( -1\right) ^{n}d^{n+1}\beta ^{n} \underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+1\right) b\omega -1 \right] }{b^{n}\omega ^{n}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-3} &=&\frac{\left( -1\right) ^{n}a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1} \underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1 \right] },\ \ \ y_{4n-2}=\frac{\left( -1\right) ^{n}b^{n}\omega ^{n}}{ d^{n}\beta ^{n-1}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+1\right) b\omega -1\right] }, \\ y_{4n-1} &=&\frac{a^{n}\gamma ^{n+1}\left( c\alpha +1\right) ^{n}}{ c^{n}\alpha ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1\right] },\ \ \ y_{4n}=\frac{b^{n}\omega ^{n+1}\left( d\beta +1\right) ^{n}}{d^{n}\beta ^{n}\underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+2\right) b\omega -1\right] }. \end{eqnarray*}
Proof. The solutions hold for \(n=0\). Now, we suppose that \(n>1\) and assume that the solutions hold for \(n-1.\) That is \begin{eqnarray*} x_{4n-7} &=&\frac{c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i\right) a\gamma -1\right] }{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}},\ \ \ x_{4n-6}=\frac{d^{n-1}\beta ^{n-1}\underset{ i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) b\omega -1\right] }{ b^{n-2}\omega ^{n-1}\left( d\beta +1\right) ^{n-1}}, \end{eqnarray*} \begin{eqnarray*} x_{4n-5} &=&\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }{ a^{n-1}\gamma ^{n-1}},\ \ \ x_{4n-4}=\frac{\left( -1\right) ^{n-1}d^{n}\beta ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) b\omega -1 \right] }{b^{n-1}\omega ^{n-1}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-7} &=&\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1 \right] },\ \ \ y_{4n-6}=\frac{\left( -1\right) ^{n-1}b^{n-1}\omega ^{n-1}}{ d^{n-1}\beta ^{n-2}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) b\omega -1\right] }, \\ y_{4n-5} &=&\frac{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{ c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1\right] },\ \ \ y_{4n-4}=\frac{b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n-1}}{d^{n-1}\beta ^{n-1}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+2\right) b\omega -1\right] }. \end{eqnarray*} Next, it can be simply seen from system (3) that \begin{eqnarray*} x_{4n-3} &=&\frac{x_{4n-5}y_{4n-7}}{y_{4n-5}\left( -1-x_{4n-5}y_{4n-7}\right) } \\ &=&\frac{\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }{ a^{n-1}\gamma ^{n-1}}\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n-1}}{ c^{n-1}\alpha ^{n-2}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }}{\frac{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i+2\right) a\gamma -1\right] }\left[ -1-\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }{a^{n-1}\gamma ^{n-1}}\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }\right] } \\ &=&-\frac{c\alpha \ c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }} \left[ \left( 2i+2\right) a\gamma -1\right] }{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}\left[ 1+c\alpha \right] }=\frac{c^{n}\alpha ^{n} \underset{i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}}. \end{eqnarray*} Furthermore, system (3) gives that \begin{eqnarray*} y_{4n-3} &=&\frac{y_{4n-5}x_{4n-7}}{x_{4n-5}\left( 1-y_{4n-5}x_{4n-7}\right) } \\ &=&\frac{\frac{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{ c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1\right] }\frac{c^{n-1}\alpha ^{n-1}\underset{i=0}{ \overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{ a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}}{\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }{a^{n-1}\gamma ^{n-1}}\left[ 1-\frac{ a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1} \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1 \right] }\frac{c^{n-1}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}\right] } \\ &=&\frac{\frac{a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1\right] }}{\frac{\left( -1\right) ^{n-1}c^{n}\alpha ^{n-1}\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }{a^{n-1}\gamma ^{n-1}}\left[ 1-\frac{a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{\underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1 \right] }\right] } \\ &=&\frac{\left( -1\right) ^{-n+1}a^{n}\gamma ^{n}\underset{i=0}{\overset{n-2} {\Pi }}\left[ \left( 2i\right) a\gamma -1\right] }{c^{n}\alpha ^{n-1} \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1 \right] \left[ \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i+2\right) a\gamma -1\right] -a\gamma \underset{i=0}{\overset{n-2}{\Pi }}\left[ \left( 2i\right) a\gamma -1\right] \right] } \\ &=&\frac{\left( -1\right) ^{n}a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\underset{ i=0}{\overset{n-1}{\Pi }}\left[ \left( 2i+1\right) a\gamma -1\right] }. \end{eqnarray*} The remaining formulas can be shown in a similar way.
2.4 Fourth System \(x_{n+1}=\frac{x_{n-1}y_{n-3}}{y_{n-1}\left( -1-x_{n-1}y_{n-3}\right) },\ y_{n+1}=\frac{y_{n-1}x_{n-3}}{x_{n-1}\left( -1+y_{n-1}x_{n-3}\right) }\)
In the next theorem, we will discover the solutions of the following nonlinear system of difference equations:Theorem 4. Assume that \(\left\{ x_{n},y_{n}\right\} \) is a solution to system (4) and let \(x_{-3}=a,\ x_{-2}=b,\ x_{-1}=c,\ x_{0}=d,\ y_{-3}=\alpha ,\ y_{-2}=\beta ,\ y_{-1}=\gamma \) and \(y_{0}=\omega .\) Then, for \(n=0,\ 1,\ ... \) we have \begin{eqnarray*} x_{4n-3} &=&\frac{\left( -1\right) ^{n}c^{n}\alpha ^{n}}{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}},\ \ \ x_{4n-2}=\frac{\left( -1\right) ^{n}d^{n}\beta ^{n}}{b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n}}, \\ x_{4n-1} &=&\frac{c^{n+1}\alpha ^{n}\left( a\gamma -1\right) ^{n}}{ a^{n}\gamma ^{n}},\ \ \ x_{4n}=\frac{d^{n+1}\beta ^{n}\left( b\omega -1\right) ^{n}}{b^{n}\omega ^{n}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-3} &=&\frac{a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n}},\ \ \ y_{4n-2}=\frac{b^{n}\omega ^{n}}{d^{n}\beta ^{n-1}\left( b\omega -1\right) ^{n}}, \\ y_{4n-1} &=&\frac{\left( -1\right) ^{n}a^{n}\gamma ^{n+1}\left( c\alpha +1\right) ^{n}}{c^{n}\alpha ^{n}},\ \ \ y_{4n}=\frac{\left( -1\right) ^{n}b^{n}\omega ^{n+1}\left( d\beta +1\right) ^{n}}{d^{n}\beta ^{n}}. \end{eqnarray*}
Proof. It is clear that the relations hold for \(n=0.\) Now, we suppose that \(n>1\) and assume that the solutions hold for \(n-1.\) That is \begin{eqnarray*} x_{4n-7} &=&\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}}{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}},\ \ \ x_{4n-6}=\frac{\left( -1\right) ^{n-1}d^{n-1}\beta ^{n-1}}{b^{n-2}\omega ^{n-1}\left( d\beta +1\right) ^{n-1} }, \\ x_{4n-5} &=&\frac{c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n-1}}{ a^{n-1}\gamma ^{n-1}},\ \ \ x_{4n-4}=\frac{d^{n}\beta ^{n-1}\left( b\omega -1\right) ^{n-1}}{b^{n-1}\omega ^{n-1}} \end{eqnarray*} and \begin{eqnarray*} y_{4n-7} &=&\frac{a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\left( a\gamma -1\right) ^{n-1}},\ \ \ y_{4n-6}=\frac{b^{n-1}\omega ^{n-1}}{d^{n-1}\beta ^{n-2}\left( b\omega -1\right) ^{n-1}}, \\ y_{4n-5} &=&\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}},\ \ \ y_{4n-4}=\frac{\left( -1\right) ^{n-1}b^{n-1}\omega ^{n}\left( d\beta +1\right) ^{n-1}}{ d^{n-1}\beta ^{n-1}}. \end{eqnarray*} Now, it can be obviously observed from system (4) that \begin{eqnarray*} x_{4n-3} &=&\frac{x_{4n-5}y_{4n-7}}{y_{4n-5}\left( -1-x_{4n-5}y_{4n-7}\right) } \\ &=&\frac{\frac{c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n-1}}{ a^{n-1}\gamma ^{n-1}}\frac{a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\left( a\gamma -1\right) ^{n-1}}}{\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}}\left[ -1-\frac{ c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n-1}}{a^{n-1}\gamma ^{n-1}} \frac{a^{n-1}\gamma ^{n-1}}{c^{n-1}\alpha ^{n-2}\left( a\gamma -1\right) ^{n-1}}\right] } \\ &=&\frac{\left( -1\right) ^{-n}c^{n}\alpha ^{n}}{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}\left[ 1+c\alpha \right] }=\frac{\left( -1\right) ^{n}c^{n}\alpha ^{n}}{a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n}}. \end{eqnarray*} Similarly, one can obtain from system (4) that \begin{eqnarray*} y_{4n-3} &=&\frac{y_{4n-5}x_{4n-7}}{x_{4n-5}\left( -1+y_{4n-5}x_{4n-7}\right) } \\ &=&\frac{\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}}\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}}{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}}{\frac{c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n-1}}{ a^{n-1}\gamma ^{n-1}}\left[ -1+\frac{\left( -1\right) ^{n-1}a^{n-1}\gamma ^{n}\left( c\alpha +1\right) ^{n-1}}{c^{n-1}\alpha ^{n-1}}\frac{\left( -1\right) ^{n-1}c^{n-1}\alpha ^{n-1}}{a^{n-2}\gamma ^{n-1}\left( c\alpha +1\right) ^{n-1}}\right] } \end{eqnarray*} \begin{eqnarray*} &=&\frac{a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n-1} \left[ -1+a\gamma \right] }=\frac{a^{n}\gamma ^{n}}{c^{n}\alpha ^{n-1}\left( a\gamma -1\right) ^{n}}. \end{eqnarray*} Other relations can be likewise proved. Therefore, this completes our proof.
2.5. Numerical Examples
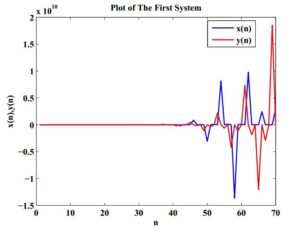
This subsection is allocated to confirm our theoretical discussion by illustrating some numerical examples. These examples show the behaviour of the solutions of each system.Example 1. In this example, we describe the behaviour of the solution of system (1). Our initial data has been taken as follows: \(x_{-3}=0.21,\ x_{-2}=-0.25,\ x_{-1}=-0.032,\ x_{0}=2,\ y_{-3}=1.06,\ y_{-2}=-0.4,\ y_{-1}=-1.55\) and \(\ y_{0}=0.082.\) See Figure 1.
Figure 1. Model of the system.
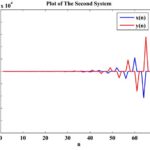
Example 2. This example demonstrates the plot of system (2). The initial values are considered as follows: \( x_{-3}=0.22,\ x_{-2}=-0.25,\ x_{-1}=0.2,\ x_{0}=0.6,\ y_{-3}=1.03,\ y_{-2}=-0.43,\ y_{-1}=1.5\) and \(\ y_{0}=0.8,\) as depicted in Figure 2.
Figure 2. Model of the system.
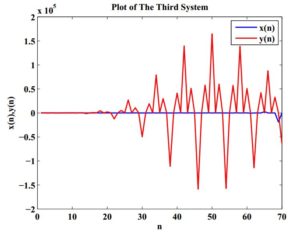
Example 3. Here, we plot the curves of solutions of system (3). Figure 3 presents this behaviour under the following initial values: \(x_{-3}=0.03,\ x_{-2}=-0.2,\ x_{-1}=10,\ x_{0}=-0.05,\ y_{-3}=2,\ y_{-2}=-4.1,\ y_{-1}=1.4\) and \(\ y_{0}=1.03.\)
Figure 3. Model of the system.
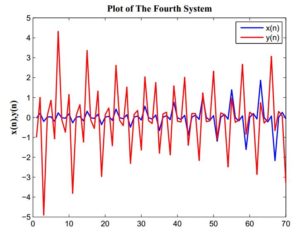
Example 4. Figure \ref{fig4} illustrates the behaviour of the solution of system (4). The considered initial conditions in this example are given as follows: \(x_{-3}=0.02,\ x_{-2}=-0.2,\ x_{-1}=0.21,\ x_{0}=-0.03,\ y_{-3}=0.1,\ y_{-2}=-4.9,\ y_{-1}=1,\ y_{0}=-1.\)
Figure 4. Model of the system.
3. Conclusion
This paper has been written to highlight the analytical and numerical solutions of four different systems of difference equations. In subsection 1, we have provided the solution of System 1 and illustrated its behaviour under specific conditions in Figure 1. Theorem 2 and Theorem 3 presented the exact solutions of System 2 and System 3, respectively. Finally, Figure 4 demonstrated the curve of the solution of System 4 which is given in Subsection 4.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- Din, Q. (2014). On a system of fourth-order rational difference equations. Acta Universitatis Apulensis, 39, 137-150. [Google Scholor]
- Asiri, A., El-Dessoky, M. M., & Elsayed, E. M. (2018). Solution of a third order fractional system of difference equations. J. Comput. Anal. Appl, 24(3), 444-453.[Google Scholor]
- Çinar, C. (2004). On the positive solutions of the difference equation system \(x_{n+1}=1/y_{n},\ \ \ y_{n+1}=y_{n}/x_{n-1}y_{n-1}\). Applied Mathematics and Computation, 2(158), 303-305.[Google Scholor]
- Din, Q. (2013). Dynamics of a discrete Lotka-Volterra model. Advances in Difference Equations, 2013(1), 95.[Google Scholor]
- El-Metwally, H., & Elsayed, E. M. (2013). Form of solutions and periodicity for systems of difference equations. Journal of Computational Analysis & Applications, 15(1), 852-857. [Google Scholor]
- Elsayed, E. M. (2012). Solutions of rational difference systems of order two. Mathematical and Computer Modelling, 55(3-4), 378-384.[Google Scholor]
- Alzubaidi, M. M., & Elsayed, E. M. The Form of the Solutions of System of Rational Difference Equation. Journal of Mathematical Sciences and Modelling, 1(3), 181-191. [Google Scholor]
- Gumus, M.,& Ocalan , O. (2018). The qualitative analysis of a rational system of difference equations. J. Fract. Calc. Appl, 9(2), 113-126. [Google Scholor]
- Kurbanli, A. S. (2011). On the behavior of solutions of the system of rational difference equations \( x_{n+1}=x_{n-1}/y_{n}x_{n-1}-1,\ y_{n+1}=y_{n-1}/x_{n}y_{n-1}-1,\ z_{n+1}=x_{n}/y_{n}z_{n-1}.\) Advances in Difference Equations, 2011(1), 1031-1038. [Google Scholor]
- Touafek, N., & Elsayed, E. M. (2012). On the solutions of systems of rational difference equations. Mathematical and Computer Modelling, 55(7-8), 1987-1997.[Google Scholor]
- Zhang, Q., Yang, L., & Liu, J. (2012). Dynamics of a system of rational third-order difference equation. Advances in Difference Equations, 2012(1), 136.[Google Scholor]
- Elsayed, E. M., & Ahmed, A. M. (2016). Dynamics of a three-dimensional systems of rational difference equations. Mathematical Methods in The Applied Sciences, 5(39), 1026-1038.[Google Scholor]
- Almatrafia, M. B., Elsayeda, E. M., & Alzahrania, F. Qualitative Behavior of Two Rational Difference Equations. Fundamental Journal of Mathematics and Applications, 1(2), 194-204.[Google Scholor]
- Almatrafi, M., & Elsayed, E. M. (2018). Solutions and Formulae for Some Systems of Difference Equations. MathLAB Journal, 1 (3) (2018), 356-369. [Google Scholor]
- Almatrafi, M. B., Elsayed, E. M., & Alzahrani, F. Qualitative Behavior of a Quadratic Second Order Rational Difference Equation. International Journal of Advances in Mathematics, 2019 (1) (2019),1-14. [Google Scholor]
- Din, Q. (2014). On a system of rational difference equation. Demonstratio Mathematica, 47(2), 324-335. [Google Scholor]
- El-Dessoky, M. M., Mansour, M., & Elsayed, E. M. (2013). Solutions of some rational systems of difference equations. Utilitas Mathematica, 92, 329-336.[Google Scholor]
- Halim, Y. (2015). Global character of systems of rational difference equations. Electronic Journal of Mathematical Analysis and Applications, 3(1), 204-214.[Google Scholor]
- Ibrahim, T. F. (2012). Two-dimensional fractional system of nonlinear difference equations in the modeling competitive populations. International Journal of Basic & Applied Sciences, 12(5), 103-121. [Google Scholor]
- Keying, L., Zhongjian, Z., Xiaorui, L., & Peng, L. (2011). More on three-dimensional systems of rational difference equations. Discrete Dynamics in Nature and Society, 2011. [Google Scholor]
- Khan, A. Q. (2014). Global behavior of an anti-competitive system of fourth-order rational difference equations. Computational Ecology and Software, 4(1), 35-46.[Google Scholor]
- Khan, A. Q., & Qureshi, M. N. (2014). Behavior of an exponential system of difference equations. Discrete Dynamics in Nature and Society, 2014. [Google Scholor]
- Khan, A. Q., & Qureshi, M. N. (2016). Global dynamics of some systems of rational difference equations. Journal of the Egyptian Mathematical Society, 24(1), 30-36. [Google Scholor]
- Ozkan, O., & Kurbanli, A. S. (2013). On a system of difference equations. Discrete Dynamics in Nature and Society. [Google Scholor]
- Phong, M. (2015). A note on a system of two nonlinear difference equations. Electronic Journal of Mathematical Analysis and Applications, 3(1), 170-179.[Google Scholor]
- Qureshi, M. N., Khan, A. Q., & Din, Q.(2014). Some Systems of Second-Order Rational Difference Equations. Life Science Journal, 11(6s), 43-50. [Google Scholor]
- Yalcinkaya, I. (2008). On the global asymptotic stability of a second-order system of difference equations. Discrete Dynamics in Nature and Society, 2008. [Google Scholor]