INFORMATION MENU
Full-Text PDF

Open Journal of Mathematical Sciences

Vol. 1 (2017), Issue 1, pp. 16 – 24
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: http://dx.doi.org/10.30538/oms2017.0002

Accretion onto Regular Magnetic Black Hole in Non-minimal Einstein-Yang-Mills Theory

A. Aslam, Piyali Bhar\(^1\)
Division of Science and Technology, University of Education, Lahore-54590, Pakistan. (A.A)
Department of Mathematics, Government General Degree College, Singur, Hooghly 712 409, West Bengal, India. (P.B)

\(^{1}\)Corresponding Author: piyalibhar90@gmail.com

Copyright © 2017 A. Aslam, Piyali Bhar. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: May 20, 2017 – Accepted: September 18, 2017 – Published: September 24, 2017

Abstract

In this work, we investigate the process of accretion for static spherical symmetric geometries for isotropic fluid. For analyze this process we use the nonminimal magnetically charged regular black holes. For this purpose, we obtain generalized expressions for the accretion rate \(\dot{M}\), critical radius \(r_s\), critical speed \(v^2_s\) and squared sound speed \(c^2_s\) during the accretion process near the regular black holes. Finally, we study the behavior of radial velocity, energy density and rate of change of mass for each
regular black hole by plotting graph.

Keywords:

isotropic fluid, black hole, radial velocity, energy density.

1. Introduction

The expansion of universe is the biggest discovery in cosmology in the epoch of 20th and 21st centuries [1, 2, 3]. Self-reliant evidence about the expansion of universe has been retrieved from Supernova type-Ia observation and large scale structure. Due to this expansion some matter produces with negative pressure as well as positive energy density [4, 5, 6, 7]. This matter is known as dark energy (DE) and its problem analyzed in [8, 9, 10, 11, 12]. The source of DE remains unfamiliar: the word 'dark' describes as it is not noticed in any observation other than gravitational measurements, and 'energy' means that this type of matter has an energy-momentum tensor.

Furthermore, the nature of DE represented by density \((\varrho)\) and pressure (p). For this, we write a ratio \(\omega=\frac{p}{\varrho}\) also noted as equation of state (EoS). Dark energy has anti-gravitational properties and its contribution is 74 percent of universe amount. Cosmological constant \(\Lambda\) with EoS parameter \(\omega=-1\) is the model of DE which is observationally perfect. But it undergoes two cosmological problems i) Fine-tuning problem: The value of DE density estimated by theoretical expectation is different to observed value, ii) Coincidence problem: The order of DE density and dark matter energy density is same [13]. To overcome the above problems, other suggested model of DE is quintessence with the range \((-1 < \omega < 1)\) [14, 15, 16, 17, 18]. By modern observational data DE also represented as phantom energy with \(\omega< -1\) [19, 20], K-essence, tachyons, chaplygin gas, etc. are also candidate of DE [21, 22, 23].

Among many predictions of general relativity (GR), the prediction of BHs is most prominent. The propensity of BHs to accrete is important consequence and so different aspects analyzed of accretion onto BHs [24]. Some astrophysicists define the accretion as the inflow of matter toward the center of object where the gravitational forces are very strong or move toward center of mass. First time the process of accretion onto compact objects studied by Bondi [25] within the Newtonian framework. Michel retrieved the same problem for relativistic results [26]. He analyzed the accretion onto Schwarzschlid BH in the context of GR and many researcher showed keen interest on his work [27, 28]. The process of accretion related to a charged BHs were investigated by [29, 30, 31].

Rodrigues and Bernardiniz [32] reviewed the effect of scalar field onto Schwarz- schlid BH which cause the change in mass of BH. Accretion of DE onto static BH has been analyzed by Kim et al. [33]. The framework of accretion onto modified Hayward BH represented by Debnath [34]. Accretion onto 3-dimensional BHs which bring up in theory of Einstein-Power-Maxwell investigated by Abbas [35]. Mart\(\acute{i}\)n-Moruno et al. work out the accretion for non-static metric onto model given by Babichev-Dokuchaev-Eroshenko [36]. Many people have also investigated the accretion formalism of DE onto different types of BHs [37, 38, 39]. Recently, Azam and Aqra discussed the accretion onto the Magnetically Charged Regular Black Hole [40].

In this work, we have used the formalism of accretion onto nonminimal magnetically charged BH, which has been analyzed by Bahamonde and Jamil [41] for regular BHs. We analyzed the consequences of regular BH mass for different values \(\omega\). This paper is organized as: In section 2, we develop the general formalism of accretion for selected BH. In section 3, We calculate the expression of velocity profile \((v(r))\), energy density \((\varrho(r))\) and rate of change regular BH mass \((\dot{M})\) and analyzed their behavior near the BH by plotting graph. Finally, we conclude the results in the last section.

2. Formalism for accretion

The nonminimal Einstien-Yang-Mills theory is described by the action
\begin{equation}\label{a} S_{NMEYM}=\int d^4x \sqrt{-g}\left[\frac{R+2\Lambda}{8 \pi}+\frac{1}{2} F_{ij}^{(a)}F^{ij(a)} +\frac{1}{2}\mathfrak{R^{ijlm}} F_{ij}^{(a)}F_{lm}^{(a)}\right], \end{equation}
(1)
where \(g\), R, \(\Lambda\) and \(8 \pi\) are the \(det(g_{ij})\), Ricci scalar, cosmological constant and coupling constant respectively, \(\mathfrak{R^{ijlm}}\) is nonminimal susceptibility tensor defined by \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \mathfrak{R^{ijlm}} &=& \frac{q_1}{2}R\left(g^{il}g^{jm}-g^{im}g^{jl}\right)+ \frac{q_2}{2}R\left(R^{il}g^{jm}-R^{im}g^{jl} +R^{jm}g^{il}-R^{jl}g^{im}\right)\\&&+q_3 R^{ijlm}, \end{eqnarray*} where, \(R^{il}\) is Ricci tensor, \(R^{ijlm}\) is Riemann tensor and \(q_1, q_2, q_3\) are the phenomenological parameters representing the nonminimal coupling of the gravitational field with Yang-Mills field. The solution of field equations by variation of the action (2) yields static spherically symmetric space-time
\begin{equation}\label{1} ds^2=-A(r)dt^{2}+A^{-1}(r)dr^{2}+r^{2}d\theta^{2} +r^2\sin^2\theta{d\phi^2}, \end{equation}
(2)
where \begin{eqnarray*} A(r)&=&1+\left(\frac{r^4}{r^4+2Q^{2}_{m}q}\right)\left(\frac{-2M}{r}+\frac{Q^{2}_{m}}{r^2}-\frac{\Lambda r^2}{3}\right), \end{eqnarray*} here q, \(Q_m\) and M are nonminimal parameter, magnetic charge and mass of object respectively. The energy-momentum tensor for perfect fluid is defined by
\begin{equation}\label{2} T^{\eta\gamma}=(\varrho+p)v^\eta v^\gamma+pg^{\eta\gamma}, \end{equation}
(3)
where \(\varrho\) is density, \(p\) is the pressure of fluid and \(v^\eta\) is four-velocity vector defined as \(v^\eta=\frac{dx^\eta}{ds}=(v^0,v^1,0,0)\) satisfy the normalization condition \(v_{\eta}v^{\eta}=-1\) yields \(v^0=\sqrt{\frac{(v^1)^2+A(r)}{A^2(r)}}\) and letting the radial velocity \(v^1=v\), we have \(v_0=g_{00}v^0=-\sqrt{v^2+A(r)}\). From Eq.(3), we obtain \(T^{1}_{0}=(\varrho+p)v_0v\). The time component of energy-momentum conservation law gives \(\frac{d}{dr}(T^1_0\sqrt{-g})=0\), which leads to
\begin{equation}\label{3} r^2v(\varrho+p)[v^2+A(r)]^{\frac{1}{2}}=B_1, \end{equation}
(4)
here \(B_1\) is constant of integration. The conservation of Eq. (3) onto fluid four-velocity i.e., \(v_\eta T^{\eta\gamma}_{;\gamma}=0,\) implies relativistic energy flux equation $$v^\eta \varrho_{,\eta}+(\varrho+p)v^\eta_{;\eta}=0,$$ which leads to
\begin{equation}\label{4} vr^2 exp\left[\int^{\varrho_h}_{\varrho_\infty}\frac{d\varrho}{\varrho+p}\right]=B. \end{equation}
(5)
Using Eqs. (4) and (5), we have
\begin{equation}\label{5} (\varrho+p)[v^2+A(r)]^{\frac{1}{2}} exp\left[-\int^{\varrho_h}_{\varrho_\infty}\frac{d\varrho}{\varrho+p}\right]=B_2, \end{equation}
(6)
where \(B_2=\frac{B_1}{B}\). Moreover, the mass flux equation of fluid $(J^\eta_{;\eta}=0)$, yields
\begin{equation}\label{6} \varrho vr^2=B_3, \end{equation}
(7)
where \(B_3=\frac{C_1}{\sin\theta}\). Substituting Eq. (7) in (4), we obtain
\begin{equation}\label{7} \frac{(\varrho+p)}{\varrho}[v^2+A(r)]^\frac{1}{2}=B_4. \end{equation}
(8)
Differentiating Eqs. (7) and (8), we have
\begin{equation}\label{9} \left[U^2-\frac{v^2}{v^2+A(r)}\right]\frac{dv}{v}+\left[2U^{2}-\frac{rA'(r)}{2(v^2+A(r))}\right]\frac{dr}{r}=0, \end{equation}
(9)
where, \(U^2=\frac{d \ln(\varrho+p)}{d \ln \varrho}-1\). From Eq.(9), equating coefficients of \(\frac{dv}{v}\) and \(\frac{dr}{r}\) equal to zero, we obtain the velocities of the fluid flow at the critical point \(r_c\)
\begin{equation}\label{10} U^2_{c}=\frac{v^2_{c}}{v^2_{c}+A(r_c)}, \end{equation}
(10)
and
\begin{equation}\label{11} \frac{4U^2_{c}}{r_c}=\frac{A'(r_c)}{v^2_{c}+A(r_c)}. \end{equation}
(11)
Here, \(v_c\) represent the critical speed of flow at \(r_c\). The expression for quantities \(U^2_c\) and \(v^2_c\) can be obtained from above equations
\begin{equation}\label{12} v^2_{c}=\frac{1}{4}r_cA'(r_c), \end{equation}
(12)
\begin{equation}\label{13} U^2_{c}=\frac{r_cA'(r_c)}{r_cA'(r_c)+4A(r_c)}. \end{equation}
(12)
The speed of sound is
\begin{equation}\label{14} \frac{dp}{d\varrho}|_{r=r_c}=c^2_{s}=B_4\sqrt{\frac{1}{v^2_{c}+A(r_c)}}-1. \end{equation}
(14)
Moreover, the rate of change of the mass of BH is defined as [35]
\begin{equation}\label{15} \dot{M}_{acc}=4 \pi B_3M^2(\varrho+p), \end{equation}
(15)
here dot serve as the derivative of mass with respect to time. The above equation shows that rate of change of BH mass purely depend on the matter distribution which accretes upon the black hole. The positivity and negativity of \((\varrho+p)\) describes the increase and decrease in mass of BH. It is shown that during accretion mechanism outside the BH mass will increase, while in Hawking radiation BH mass decreases for fluid like phantom dark energy [41].

3. Nonminimal Magnetically Charged RBH

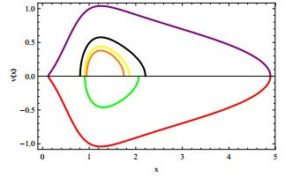
In this section, we apply the formalism accretion onto BH develop in the above section to RBH. The velocity and energy density of fluid flow can be obtain with Eqs. (4) and (7) in the scenario of barotropic EoS (\(p(r)=\omega \varrho(r)\))
\begin{equation}\label{16} v(r)=\frac{\left[-A(r)(\omega+1)^2+B^2_{4}\right]^\frac{1}{2}}{\omega+1}, \end{equation}
(16)
and
\begin{equation}\label{17} \varrho(r)=\frac{B_3 (\omega+1)}{r^2\left[-A(r)(\omega+1)^2+B^2_{4}\right]^\frac{1}{2}}. \end{equation}
(17)
Now, the rate of change of RBH mass for a barotropic fluid with Eqs. (15) and (17) in the accretion process turns out to be
\begin{equation}\label{18} \dot{M}=\frac{4\pi B_4 B^2_{3} (\omega+1)}{r^2\left[-A(r)(\omega+1)^2+B^2_{4}\right]^\frac{1}{2}}. \end{equation}
(18)

Now, we plot the graph for above expression to analyze behavior of fluid near the BH. Figure \textbf{1} shows the velocity profile for different values of \(\omega\). The value of \(\omega\) represent the various models of DE such that for cosmological constant \(\omega=1\), dust \(\omega=0\), stiff \(\omega=-1\), phantom energy \(\omega < -1\) and quintessence \(-1< \omega < 1\). It is noted that the behavior of velocity is similar to those reported in [41, 42]. Also, we have found that velocity is positive for \(\omega \geq -0.5\) and negative for phantom energy \((\omega < -1)\). The rest position of fluid depends upon the value of \(\Lambda\) and it would be changed for different values of $\Lambda$. For instance, fluid attain its rest position at \(x=5\) for \(\Lambda=-0.05\).

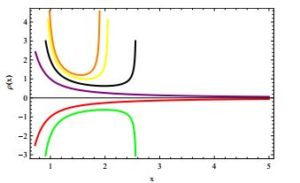
Figure 2 shows the behavior of energy density of fluid near the BH for electing different values of \(\omega\). It shows that energy density is negative for \(\omega=-1.5\) and \(\omega=-2\) and positive for other values of \(\omega\). It approaches to zero (\(\varrho \rightarrow 0\)) at infinity, while due to strong gravitational interaction approach to maximum near the BH.

Velocity profile of fluid against \(x=\frac{r}{M}\) for \(B_4=0.5\), \(q=1.5\), \(Q_{m}=0.5\), \(\Lambda=-0.05\) and various value of \(\omega\) i.e., -2(Green), -1.5(Red), -0.5(Purple), 0(Black), 0.5(Yellow), 1(Orange) for the magnetically charged BH.

Energy density of fluid against \(x=\frac{r}{M}\) for \(B_3=1\), \(B_4=0.5\), \(q=1.5\), \(Q_{m}=0.5\), \(\Lambda=0.01\) and various value of \(\omega\) i.e., -2(Green), -1.5(Red), -0.5(Purple), 0(Black), 0.5(Yellow), 1(Orange) for the magnetically charged BH.

Rate of change of RBH mass against \(x=\frac{r}{M}\) for \(B_3=1\), \(B_4=0.5\), \(q=1\), \(Q_{m}=1.5\), \(\Lambda=0.5\) and various value of \(\omega\) i.e., -2(Green), -1.5(Red), -0.5(Purple), 0(Black), 0.5(Yellow), 1(Orange) for the magnetically charged BH.

Figure 3 shows the rate of change of RBH mass for different value of \(\omega\). In this case, the profile of accreting mass of nonminimal RBH is similar to the profile for charged BH in string theory [41], which shows that the mass of RBH as a result of accretion of dust, stiff and quintessence matter increases and reverse case will be occur for phantom energy.

Conclusions

We have discussed the accretion process for the non-minimal magnetically charged RBH. We have followed same method as discussed in Bahamonde and Jamil [41] and analyzed the behavior of different aspects of fluid flow (velocity, energy density and accretion rate \(\dot{M}\)) near the BH. Moreover, we considered all type of fluid satisfy the EoS with obvious value of \(\omega\). Also, we formulate the link between energy-momentum conservation law and barotropic EoS. Furthermore, the EoS classify which sort of fluid is tumbling onto BH. In peculiar, we do not deal with cosmological constant because the expansion of BHs do not effected by its accretion. Thus, we concentrate on other candidate of DE. These candidate of DE cause the negative or positive behavior of energy density near the BH. It can be analyzed by plotting rate of change of RBH mass that the mass of BH decreases or increases due to dust and stiff or phantom like fluid respectively. In future work, we will formulate same formalism for non static fluid.

Competing Interests

The author(s) do not have any competing interests in the manuscript.

References

  1. Perlmutter, S. (2012). Nobel Lecture: Measuring the acceleration of the cosmic expansion using supernovae. Reviews of Modern Physics, 84(3), 1127-1149. [Google Scholor]
  2. Schmidt, B. P. (2012). Nobel Lecture: Accelerating expansion of the Universe through observations of distant supernovae. Reviews of Modern Physics, 84(3), 1151-1163. [Google Scholor]
  3. Riess, A. G. (2012). Nobel Lecture: My path to the accelerating Universe. Reviews of Modern Physics, 84(3), 1165-1175.[Google Scholor]
  4. Bahcall, N. A., Ostriker, J. P., Perlmutter, S. & Steinhardt, P. J. (1999). The cosmic triangle: Revealing the state of the universe. Science, 284(5419), 1481-1488. [Google Scholor]
  5. Riess, A. G. et al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal, 116(3), 1009-1038. [Google Scholor]
  6. Perlmutter, S. et al. (1999). Measurements of \(\Omega\) and \(\Lambda\) from 42 high-redshift supernovae. The Astrophysical Journal, 517(2), 565-586.[Google Scholor]
  7. Bennett, C. L. et al. (2003). First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. The Astrophysical Journal Supplement Series, 148(1), 1-27. [Google Scholor]
  8. Chernin, A. D. (2008). Dark energy and universal antigravitation. Physics-Uspekhi, 51(3), 253-282. [Google Scholor]
  9. Chernin, A. D. (2013). Dark energy in the nearby Universe: HST data, nonlinear theory, and computer simulations. Physics-Uspekhi, 56(7), 704-709. [Google Scholor]
  10. Lukash, V. N. & Rubakov, V. A. E. (2008). Dark energy: myths and reality. Physics-Uspekhi, 51(3), 283-289. [Google Scholor]
  11. Bolotin, Y. L., Erokhin, D. A. & Lemets, O. A. (2012). Expanding Universe: slowdown or speedup?. Physics-Uspekhi, 55(9), 876-918. [Google Scholor]
  12. Copeland, E. J., Sami, M. & Tsujikawa, S. (2006). Dynamics of dark energy. International Journal of Modern Physics D, 15(11), 1753-1935.[Google Scholor]
  13. Yoo, J. & Watanabe, Y. (2012). Theoretical models of dark energy. International Journal of Modern Physics D, 21(12), 1230002. [Google Scholor]
  14. Wetterich, C. (1988). Cosmology and the fate of dilatation symmetry. Nuclear Physics B, 302(4), 668-696. [Google Scholor]
  15. Peebles, P. J. E. & Ratra, B. (1988). Cosmology with a time-variable cosmological constant. The Astrophysical Journal, 325, L17-L20. [Google Scholor]
  16. Caldwell, R. R., Dave, R. & Steinhardt, P. J. (1998). Cosmological imprint of an energy component with general equation of state. Physical Review Letters, 80(8), 1582-1585. [Google Scholor]
  17. Ratra, B. & Peebles, P. J. (1988). Cosmological consequences of a rolling homogeneous scalar field. Physical Review D, 37(12), 3406-3427. [Google Scholor]
  18. Frieman, J. A., Hill, C. T., Stebbins, A. & Waga, I. (1995). Cosmology with ultralight pseudo Nambu-Goldstone bosons. Physical Review Letters, 75(11), 2077-2080. [Google Scholor]
  19. Caldwell, R. R. (2002). A phantom menace? Cosmological consequences of a dark energy component with super-negative equation of state. Physics Letters B, 545(1), 23-29. [Google Scholor]
  20. Caldwell, R. R., Kamionkowski, M. & Weinberg, N. N. (2003). Phantom energy: dark energy with \(w< - 1\) causes a cosmic doomsday. Physical Review Letters, 91(7), 071301, 1-4. [Google Scholor]
  21. Nojiri, S. I. & Odintsov, S. D. (2011). Unified cosmic history in modified gravity: from \(F(R)\) theory to Lorentz non-invariant models. Physics Reports, 505(2), 59-144. [Google Scholor]
  22. Elizalde, E. & Hildebrandt, S. R. (2002). Family of regular interiors for nonrotating black holes with \(T_{00}= T_{11}\). Physical Review D, 65(12), 124024. [Google Scholor]
  23. Gasperini, M., Piazza, F. & Veneziano, G. (2001). Quintessence as a runaway dilaton. Physical Review D, 65(2), 023508, 1-31. [Google Scholor]
  24. Chakrabarti, S. K. (1996). Accretion processes on a black hole. Physics Reports, 266(5-6), 229-390. [Google Scholor]
  25. Bondi, H. J. (1952). On spherically symmetrical accretion. Monthly Notices of the Royal Astronomical Society, 112(2), 195-204. [Google Scholor]
  26. Michel, F. C. (1972). Accretion of matter by condensed objects. Astrophysics and Space Science, 15(1), 153-160. [Google Scholor]
  27. Ray, D. (1980). Accretion of gas by a Schwarzchild black hole. Astronomy and Astrophysics, 82, 368-369.
  28. Begelman, M. C. (1978). Accretion of \(v>5/3\) gas by a schwarzschild black hole. Astronomy and Astrophysics, 70, 583-584. [Google Scholor]
  29. Babichev, E. O., Dokuchaev, V. I. & Eroshenko, Y. N. (2011). Perfect fluid and scalar field in the Reissner-Nordström metric. Journal of Experimental and Theoretical Physics, 112(5), 784-793.[Google Scholor]
  30. Jamil, M., Qadir, A., Rashid, M. A. (2008). Charged black holes in phantom cosmology. The European Physical Journal C-Particles and Fields, 58(2), 325-329. [Google Scholor]
  31. Sharif, M. & Abbas, G. (2011). Phantom Accretion by Five-Dimensional Charged Black Hole. Modern Physics Letters A, 26(23), 1731-1736. [Google Scholor]
  32. Rodrigues, M. G. & Bernardini, A. E. (2012). Accretion of Nonminimally Coupled Generalized Chaplygin Gas Into Black Holes. International Journal of Modern Physics D, 21(09), 1250075. [Google Scholor]
  33. Kim, S. W. & Kang, Y. (2012). Dark Energy and Dark Matter Accretion Onto A Black Hole in Expanding Universe. International Journal of Modern Physics: Conference Series, 12, 320-329.[Google Scholor]
  34. Debnath, U. (2015). Accretion and evaporation of modified Hayward black hole. The European Physical Journal C, 75(3), 129. [Google Scholor]
  35. Abbas, G. & Ramzan, R. M. (2013). Thermodynamics of Phantom Energy Accreting onto a Black Hole in Einstein—Power—Maxwell Gravity. Chinese Physics Letters, 30(10), 100403.[Google Scholor]
  36. Martín-Moruno, P. & Madrid, J. A. J., González-Díaz, P. F. (2006). Will black holes eventually engulf the Universe?. Physics Letters B, 640(4), 117-120. [Google Scholor]
  37. Martín-Moruno, P., Marrakchi, A. E. L., Robles-Pérez, S. & González-Díaz, P. F. (2009). Dark energy accretion onto black holes in a cosmic scenario. General Relativity and Gravitation, 41(12), 2797-2811. [Google Scholor]
  38. Sharif, M. & Abbas, G. (2011). Phantom accretion onto the Schwarzschild de-Sitter black hole. Chinese Physics Letters, 28(9), 090402. [Google Scholor]
  39. Nayak, B. & Jamil, M. (2012). Effect of vacuum energy on evolution of primordial black holes in Einstein gravity. Physics Letters B, 709(3), 118-122. [Google Scholor]
  40. Azam, M. & Aslam, A. (2017). Accretion onto the Magnetically Charged Regular Black Hole. Chinese Physics Letters, 34(7), 070401. [Google Scholor]
  41. Bahamonde, S. & Jamil, M. (2015). Accretion processes for general spherically symmetric compact objects. The European Physical Journal C, 75(10), 508. [Google Scholor]
  42. Babichev, E. O., Dokuchaev, V. I. & Eroshenko, Y. N. (2013). Black holes in the presence of dark energy. Physics-Uspekhi, 56(12), 1155-1175. [Google Scholor]
Category: OMS - Vol 1 - 2017