Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI:10.30538/oms2017.0005
The Generalized Zagreb Index of Capra-Designed Planar Benzenoid Series \(Ca_k(C_6)\)
Muhammad S. Sardar, Sohail Zafar, Mohammad R. Farahani\(^1\)
Department of Mathematics, University of Management and Technology (UMT), Lahore, Pakistan. (M.S.S & S.Z)
Department of Applied Mathematics, Iran University of Science and Technology(IUST), Narmak, Tehran 16844, Iran. (M.R.F)
\(^{1}\)Corresponding Author: mr_farahani@mathdep.iust.ac.ir
Abstract
Keywords:
1. Introduction
Let \(G=(V,E)\) be a simple connected graph of finite order \(n=|V|=|V(G)|\) with the set of vertices and the set of edges \(E=E(G)\). We denote by \(d_v\), the degree of a vertex \(v\) of \(G\) which is defined as the number of edges incident to \(v\). A general reference for the notation in graph theory is [1]. A molecular graph is a simple finite graph such that its vertices correspond to the atoms and the edges to the bonds.
In chemistry, graph invariants are known as topological indices. In graph theory, we have many different topological indices of arbitrary graph \(G\). A topological index of a graph is a number related to a graph which is invariant under graph automorphisms. Obviously, every topological index defines a counting polynomial and vice versa.
The Wiener index \(W(G)\) is the oldest based structure descriptor [2, 3, 4], introduced by Harold Wiener in 1947, is the first topological index in chemistry. The Wiener index of \(G\) is defined as the sum of distances between all pairs of vertices of \(G\) and is equal as follow: \begin{eqnarray*}\label{F1} W(G) &=& \frac{1}{2} \sum \limits_{(u,v)} d(u,v). \end{eqnarray*} where \((u,v)\) is any ordered pair of vertices in \(G\) and \(d(u,v)\) is \(u-v\) geodesic.
The Zagreb index was defined about forty years ago by I. Gutman and N. Trinajstic in 1972 [5] (or, more precisely, the First Zagreb index, because there exists also a Second Zagreb index [4]). The First Zagreb index of \(G\) is defined as the sum of the squares of the degrees of all vertices of \(G\) [6,7]. The first and second Zagreb indices of \(G\) are denoted by \(M_1(G)\) and \(M_2(G)\), respectively and defined as follows: \begin{eqnarray*} M_1(G) &=& \sum_{u \in V(G)} d_u^2 \hspace{10mm} \mbox{and} \hspace{10mm}\\ M_2(G) &=& \sum_{uv \in E(G)} d_{u}d_{v}. \end{eqnarray*} In fact, one can rewrite the first Zagreb index as $$M_1(G)=\sum_{uv \in E(G)} \big[ d_u+d_v \big].$$ where \(d_u\) and \(d_v\) are the degrees of \(u\) and \(v\), respectively. In 2011, M. Azari and A. Iranmanesh [8] introduced the generalized Zagreb index of a connected graph \(G\), based on degree of vertices of \(G\). The Generalized Zagreb index of \(G\) is defined for arbitrary non-negative integer \(r\) and \(s\) as follows: $$M_{(r,s)}(G)=\sum_{uv \in E(G)} \big[ d_u^rd_v^s+d_u^sd_v^r \big].$$
In [8], A. Iranmanesh and M. Azari expressed some of the obvious properties of the Generalized Zagreb index of a graph \(G\).Theorem 1.1. [8] Let \(G\) be a graph with the vertex and edge sets \(V(G)\) and \(E(G)\). Some of the properties of the generalized Zagreb index of \(G\) are as
- \(M_{(0,0)}(G)=2\sum_{v \in V(G)}=2|E(G)|\).
- \(M_{(1,0)}(G)=M_1(G)\).
- \(M_{(r-1,0)}(G)=\sum_{v \in V(G)}dv^r\).
- \(M_{(1,1)}(G)=2M_2(G)\).
- \(M_{(r,r)}(G)=2 \sum_{uv \in E(G)}(d_u\times d_v)^r\).
2. What is the Capra Operation?
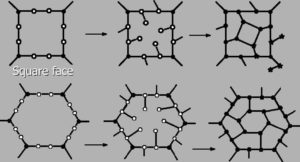
A mapping is a new drawing of an arbitrary planar graph \(G\) on the plane. In graph theory, there are many different mappings (or drawing); one of them is Capra operation. This method enables one to build a new structure of a planar graph \(G\).
Let \(G\) be a cyclic planar graph. Capra map operation is achieved as follows:
- insert two vertices on every edge of \(G\);
- add pendant vertices to the above inserted ones and
- connect the pendant vertices in order \((-1,+3)\) around the boundary of a face of \(G\). By runing these steps for every face/cycle of \(G\), one obtains the Capra-transform of \(G\) \(Ca(G)\), see Figure 1.
This method was introduced by M.V. Diudea and used in many papers [9, 10, 11, 12, 13, 14, 15, 16]. Since Capra of planar benzenoid series has a very remarkable structure, we lionize it.
We denote Capra operation by \(Ca\), in this paper, as originally Diudea did. Thus, Capra operation of arbitrary graph \(G\) is \(Ca(G)\), iteration of Capra will be denoted by \(CaCa(G)\) (or we denote \(Ca_2(G))\) (Figures 2 and 3).
The benzene molecule is a usual molecule in chemistry, physics and nano sciences. This molecule is very useful to synthesize aromatic compounds. We use the Capra operation to generate new structures of molecular graph benzene series.
In this paper, we focus on the the structure of Capra-designed planar benzenoid series \(Ca_k(C_6)\), \(k\geq0\) and compute its generalized Zagreb index.
An example of Capra map operation on the hexagon face. Since Capra of planar benzenoid series has a very remarkable structure, we lionize it.
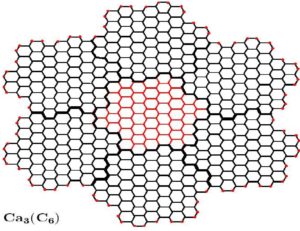
The first two graphs \(Ca(C_6)\) and \(Ca_2(C_6)\) from the Capra of planar benzenoid series, together with the molecular graph of benzene \(C_6\). Benzene is equivalent with \(Ca_0(C_6)\).
Graph \(Ca_3(C_6)\) is the third member of Capra-designed planar benzenoid series \(Ca_k(C_6)\).
3. Main Results
Capra transforms of a planar benzenoid series is a family of molecular graphs which are generalizations of benzene molecule \(C_6\). In other words, we consider the base member of this family is the planar benzene, denoted here \(Ca_0(C_6)=C_6=\) benzene. It is easy to see that \(Ca_k(C_6)=Ca(Ca_{k-1}(C_6))\) (Figures 2 and 3) ([9, 10, 11, 12, 13, 14, 15, 16]). In addition, we need the following notions [17]. Let \(G\) be a molecular graph and \(d_v\) is the degree of vertex \(v\in V(G)\). We divide vertex set \(V(G)\) and edge set \(E(G)\) of graph \(G\) to several partitions, as follow:
\(\forall i\), \(\delta < i< \Delta\), \(V_i=\{v \in V(G) |d_v=i\}\),and \(\forall k, \delta^2\leq k\leq \Delta^2, E^*_k=\{e=uv\in E(G)|d_v\times d_u=k\}\).
Obviously, \(1\leq\delta\leq d_v\leq\Delta\leq n-1\) such that \(\delta=Min\{d_v|v\in V(G)\}\) and \(\Delta=Max\{d_v|v\in V(G)\}\).
Theorem 3.1. Consider the graph \(G=Ca_k(C_6)\) as the iterative Capra of planar benzenoid series. Then: $$ M_{(r,s)}=3(7^k-2(3^{k-1})-1)\times \big[ 2(3^{r+s}) \big]+4(3^k) \times\big[ 2^r3^s+2^s3^r \big]+3(3^{k-1}+1)\times \big[2(2^{r+s}) \big]. $$
Proof.
Consider the Capra of planar benzenoid series \(G=Ca_k(C_6)\) \((k\geq1)\). By construction, the structure \(Ca_k(C_6)\) collects seven times of structure \(Ca_k-1(C_6)\) (we call "flower" the substructure \(Ca_{k-1}(C_6)\) in the graph \(Ca_k(C_6))\). Therefore, by simple induction on \(k\), the vertex set of \(Ca_k(C_6)\) will have \(7\times|V(Ca_k(C_6))|-6(2\times3^{k-1}+1)\) members. Because, there are \(3^{k-1}+1\) and \(3^{k-1}\) common vertices between seven flowers \(Ca_{k-1}(C_6)\) in \(Ca_k(C_6)\), marked by full black color in the above figures. Similarly, the edge set \(E(Ca_k(C6))\) have \(7\times|E(Ca_k(C_6))|-6(2×3^{k-1}+1)\) members. Since, there are \(3^{k-1}\) and \(3^{k-1}\) common edges (full black color in these figures).
Now, we solve the recursive sequences \(|V(Ca_k(C_6))|\) and \(|E(Ca_k(C_6))|\). First, suppose \(n_k=|V(Ca_k(C_6))|\) and \(e_k=|E(Ca_k(C_6))|\)
so \(n_k=7n_{k-1}-4(3^k)-6\) and \(e_k=7e_{k-1}-4(3^k)\). Thus, we have
\(n_k=7n_{k-1}-4ò_k-6\)
\(=7(7n_{k-2}-4ò_{k-1}-6)-4ò_k-6\)
\(=7^2n_{k-2}-7(4ò_{k-1}+6)-(4ò_k+6)\)
\(=7^3n_{k-3}-7^2(4ò_{k-2}+6)-7(4ò_{k-1}+6)-(4ò_k+6)\)
.
.
.
\(=7^in_{k-i}-7^{i-1}(4ò_{k-(i-1)}+6)-...-7(4ò_{k-1}+6)-(4ò_k+6)\)
\(=7^in_{k-i}-\sum^{i-1}_{j=0}7^j(4ò_{k-j}+6)\)
.
.
.
\(=7^kn_{k-k}-\sum^{k-1}_{i=0}7^i(4ò_{k-i}+6)\)
\((\alpha-\beta)\sum^n_{i=0}\alpha^i\beta^{n-1}=(\alpha-\beta)(\alpha^0\beta^n+\alpha^1\beta^{n-1}+...+\alpha^{n-1}\beta^1+\alpha^n\beta^0)=(\alpha^{n+1}-\beta^{n+1})\) Hence
\(\sum^{k-1}_{i=0}7^i3^{k-i}=(7^03^k+7^13^{k-1}+...+7^{k-2}3^2+7^{k-1}3^1)+7^k3^0-7^k3^0\)
\(=\frac{7^{k+1}-3^{k+1}}{7^1-3^1}-7^k3^0\)
\(=\frac{7^{k+1}-3^{k+1}-4(7^k)}{4}\)
\(=\frac{3(7^k-3(3^k))}{4}\)
\(n_k=6\times7^k-(4(\frac{3}{4}(7^k-3^k))+(7^k-1))\) and \(\forall k\geq0, n_k=|V(Ca_k(C_6))|=2\times7^k+3^{k+1}+1. \)
By using a similar argument and (1), we can see that
\(e_k=7e_{k-1}-4ò=7^2e_{k-2}-7(4ò_{k-1})-4ò.\)
.
.
.
\(=7^ke_{k-k=0}-4\sum^{k-1}_{i=0}7^iò_{k-i}=7^ke_0-4\sum^{k-1}_{i=0}7^i3^{k-i}\).
It is easy to see that, the first member of recursive sequence \(e_k\) is \(e_0=6\), (Figure 2). Now, by using (2), we have \(e_k=6\times7^k-4(\frac{3}{4}(7^k-3^k))\) and the size of edge set \(E(Ca_k(C_6))\) is equal to: \(e_k=|E(Ca_k(C_6))|=3(^7k+3^k)\), \(\forall k\geq0\).
Also, according to Figures 2 and 3, we see that the number of vertices of degree two in the graph \(Ca_k(C_6)\) (we denote by \(v^{(k)}_2\) ) is equal to \(6\times3(\frac{(v_2^{(k-1))}}{6})-6\). The six removed vertices are the common ones between the six flowers \("Ca_{k-1}(C_6)"\) with degree three. By using a similar argument and simple induction, we have \(v_2^{k-1}\) the numbers of edges of graph \(Ca_k(C_6)\), which are in the set \(E_4\) or \(E_4^*\) (denoted by \(e_4^{(k)}\)).
Now, we solve the recursive sequence \(v_2^{(k)}=6(3(\frac{v_2^{(k-1)}}{6})-1)\) and we conclude \(v_2^{k}=3v_2^{(k-1)}-6=3(3v_2^{(k-2)}-6)-6=...=3^kv_2^{(0)}-6\sum^{k-1}_{i=0}3^i\).
It is obvious that, according to the structure of benzene, \(v_2^{(0)}=n_0=6\). Thus, \(v_2^{(k)}=6\times3^k-6(\frac{3^k-1}{3-1})=3^k+1+3.\)
Also, \(e_4^{(k)}=|E_4|=|E_4^*|=v_2^{(k-1)}=3^{k+1}+3\) and according to the above definition, it is obvious that, for Capra of planar benzenoid series \(G=Ca_k(C_6)\) we have two partitions: \(V_2=\{v\in V(Ca_k(C_6))|d_v=2\}\) and \(V_3=\{v\in V(Ca_k(C_6))|d_v=3\}\) with the size \(3^{k+1}+3\) and \(2(7^k-1)\) respectively.
On the other hand, according to the structure of Capra planar benzenoid series \(Ca_k(C_6)\), there are \(2v_2^{(k)}\) edges, such that the first point of them is a vertex with degree two. Among these edges, there exist \(v_2^{k-1}\) edges, of which the first and end point of them have degree 2 (the members of \(E_4\) or \(E_4^*\) ).
Thus, \(e_5^{(k)}=|E_5|=|E_6^*|=2v_2^{(k)}-2e_4^{(k)}=2v_2^{(k)}-2v_2^{(k-1)}\). So, the size of edge set \(E_5\) and \(E_6^*\) is equal to \(e_5^{k}=2(3^{k+1}+3-3^k-3)=4(3^k)\).
Now, it is obvious that:
\(e_6^{(k)}=|E_6|=|E_9^*|=3(7^k+3^k)-e_5^{(k)}-e_4^{(k)}\)
\(=3\times7^k+3^{k+1}-4\times3^k-3^k-3\)
\(=3\times7^k-2\times3^k-3\)
\(={3(7^k-2(3^{k-1})-1)}.\)
Now, we know the size of all sets \(V_2, V_3, E_4, E_4^*, E_5, E_6^*, E_6\) and \(E_9^*\). So, we can calculate the Generalized Zagreb Index Of Capra planar benzenoid series \(G=Ca_k(C_6)\), as follow:
Thus, we have following computations for the generalized Zagreb index of Capra planar benzenoid series \(G=Ca_k(C_6)\) $$M_{(r,s)}(G)=\sum_{uv \in E(G)} \big[ d_u^rd_v^s+d_u^sd_v^r \big] $$ $$=\sum_{uv \in E(G)} \big[ 3^r3^s+3^s3^r \big]+\sum_{uv \in E(G)} \big[ 2^r3^s+2^s3^r \big]+\sum_{uv \in E(G)} \big[ 2^r2^s+2^s2^r \big] $$ $$=\sum_{uv \in E(G)} \big[ 2(3^{r+s}) \big]+\sum_{uv \in E(G)} \big[ 2^r3^s+2^s3^r \big]+\sum_{uv \in E(G)} \big[2(2^{r+s})\big] $$ $$=3(7^k-2(3^{k-1})-1)\times \big[ 2(3^{r+s}) \big]+4(3^k) \times\big[ 2^r3^s+2^s3^r \big]+3(3^{k-1}+1)\times \big[2(2^{r+s}) \big].$$ Thus, we completed the proof of the theorem.
Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20. [Google Scholor]
- Dobrynin, A. A., Entringer, R., & Gutman, I. (2001). Wiener index of trees: theory and applications. Acta Applicandae Mathematica, 66(3), 211-249. [Google Scholor]
- Needham, D. E., Wei, I. C., & Seybold, P. G. (1988). Molecular modeling of the physical properties of alkanes. Journal of the American Chemical Society, 110(13), 4186-4194.[Google Scholor]
- Rücker, G., & Rücker, C. (1999). On topological indices, boiling points, and cycloalkanes. Journal of chemical information and computer sciences, 39(5), 788-802. [Google Scholor]
- Gutman, I., & Trinajstić, N. (1972). Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17(4), 535-538.[Google Scholor]
- Gutman, I., & Das, K. C. (2004). The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem, 50(1), 83-92.[Google Scholor]
- Gutman, I., Ruščić,, B., Trinajstić, N., & Wilcox, C. F. (1975). Graph theory and molecular orbits.XII. Acyclic polyenes. J. Chem. Phys, 62, 3399-3405.[Google Scholor]
- Azari, M., & Iranmanesh, A. (2011). Generalized Zagreb index of graphs. Studia Universitatis Babes-Bolyai, Chemia, 56(3), 59-70.[Google Scholor]
- Goldberg, M. (1937). A class of multi-symmetric polyhedra. Tohoku Mathematical Journal, First Series, 43, 104-108. [Google Scholor]
- Dress, A., & Brinkmann, G. (1996). Phantasmagorical fulleroids. MATCH Commun. Math. Comput. Chem, 33, 87-100.[Google Scholor]
- Diudea, M. V. (2005). Nanoporous carbon allotropes by septupling map operations. Journal of chemical information and modeling, 45(4), 1002-1009. [Google Scholor]
- Diudea, M. V., Stefu, M., John, P. E., & Graovac, A. (2006). Generalized operations on maps. Croatica chemica acta, 79(3), 355-362. [Google Scholor]
- Farahani, M. R., & Vlad, M. P. (2012). On the Schultz, Modified Schultz and Hosoya polynomials and Derived Indices of Capra-designed planar Benzenoids. Studia UBB Chemia, 57(4), 55-63. [Google Scholor]
- Farahani, M. R. (2012). Computing \(ABC_{4}\) index of Capra-designed planar benzenoid series \(Ca_{k}(C_{6})\). Advances in Materials and Corrosion, 1(1), 61-64. [Google Scholor]
- Farahani, M. R. (2013). On the Schultz polynomial and Hosoya polynomial of circumcoronene series of Benzenoid. Journal of Applied Mathematics & Informatics, 31(5-6), 595-608. [Google Scholor]
- Farahani, M. R. (2013). A new version of Zagreb index of circumcoronene series of benzenoid. Chemical Physics Research Journal, 6(1), 27-33. [Google Scholor]
- Farahani, M. R. (2012). Some connectivity indices and Zagreb index of polyhex nanotubes. Acta Chim. Slov, 59, 779-783. [Google Scholor]