Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2021.0145
Inequalities approach in determination of convergence of recurrence sequences
Albert Adu-Sackey, Francis T. Oduro, Gabriel Obed Fosu\(^1\)
Department of Applied Mathematics, Koforidua Technical University, Ghana.; (A.A.S)
African Institute for Mathematical Sciences, Ghana.; (F.T.O)
Department of Mathematics, Presbyterian University College, Ghana.; (G.O.F)
\(^{1}\)Corresponding Author: gabriel.obed@presbyuniversity.edu.gh
Abstract
Keywords:
1. Introduction
Sequences could be defined in many forms, however, most sequences may be quite difficult to establish closed formulas for their forms. Nonetheless, it is often easier or much preferable to express sequences by recursive definitions. It is essential to note that some recursive relations are adaptive and could be converted into closed formulas devoid of a recurrence relation. By [1,2,3,4,5,6,7] a recurrence relation is an equation that inductively defines a successive term of a sequence in terms of one or more preceding term(s) of the sequence. Notably, some useful applications of recurrence relation can be seen in the study of models involving population growth, investments, depreciation, algorithm analysis, digital signal processing, and cryptography.
In this paper, we shall consider the following special sequences;
- (I) \( u_{n+1} = \dfrac{a}{b} u_{n} + c \),
- (II) \( u_{n+1} = \dfrac{1}{2} \left( u_{n} + \dfrac{a}{u_{n}} \right) \),
- (III) \( u_{n+1} = \sqrt{a + \sqrt{u_{n}}} \).
The consideration of the sequence (I) is its usefulness. This will afford us the advantage of thoroughly illustrating its flexibility in drumming home the processes involve in showing that a given sequence is convergent. Also, due to the practicality of the sequence (II) we will demonstrate and prove a general bound for this important sequence without inferring from the monotone convergence theorem, although it is always implied. The determination of a supremum or an infimum could be a daunting prospect. Such a theorem is invoked because it asserts that, if by some means we are able to know just the upper (lower) bound and along with a possible fact that a sequence is monotonic increasing(decreasing), then convergence is guaranteed and the limit exists, as is often the case in literature [8,9,10,11]. Similarly, for the nested recurrence sequence (III), we shall meticulously demonstrate how one could use arithmetic arguments and bi-quadratic equation rather than mathematical induction to prove their boundedness, monotone property, and the general limit to which they converge to. The motivation is garnered to challenge and encourage real analysis students that, there is no one size fit approach in tackling convergence and to introduce some flavor of using basic inequalities of algebra and equations to achieve convergence for a given well-defined recursive sequence. This is neither to downplay the applications of the monotone convergence theorem that is usually adopted without necessarily having to obtain a bound and to prove it for the particular sequence being investigated upon, nor to discourage the use of mathematical induction, but rather to logically use arguments involving inequalities to explore monotonic properties and boundedness especially for sequences defined recursively under the radical symbol.
2. Literature review
The concept we seek to explore is deeply rooted in the qualitative research paradigm, and hence the need to review the works of earlier authors at least on the convergence of a sequence and in particular sequences that are defined inductively by a recurrence relation.The sequence of the form \( u_{n} = au_{n-1} + b \) is a first-order difference equation, in the sense that we are looking back one unit in time to \( u_{n-1} \) with its exponentiation being unity. This sequence has two main characterizations as far as the nomenclature of their classification is concerned. For instance when \( a = 1 \) the resulting recurrence relation leads to \( u_{n} = u_{0} + nb \) a closed-form formula of a special class of sequence referred to as arithmetic progression, and when \( a \ne 1 \), it transforms into another special class of sequence known as geometric progression with a closed formula given by \( u_{n} -k = a^{n} (u_{0}-k) \) with \( k = b/(1-a) \).
One can observe that if the initial preceding term \( u_{0} = k \), then the geometric characterization collapses and the sequence fall into a different classification altogether known as a constant sequence.
A careful study of this type of difference equation provides a qualitative insight into the convergence of many other types of sequences. It is because of this instance that such an important recurrence algorithm has earned the name, the arithmetico-geometric sequence. Such a sequence posses the same intrinsic properties in connection with the general case of the sequence type (I). As such we shall develop a contractive sequence for their kind to enable us to investigate it further.
From a practical viewpoint, a successive approximation method or iteration that comes up in the area of numerical analysis is in the evaluation of the square root of a given real number '\( a \)'. Such a procedure is developed upon the fact that if \( x \) is exactly equal to \( \sqrt{a} \), so is the quotient of \( a/x \). On the contrary, regardless of how \( x \) and \( a/x \) are less or greater than \( \sqrt{a} \), the square root of the real number '\( a \)' will always lie between \( x \) and \( a/x \) [12,13,14]. Thus, the arithmetic mean of these two uniquely defined numbers can fairly be expressed as a fixed point equation or a recursive sequence with an initial guess \( x_{1} = x_{0} \) assumed to be a good approximate to \( \sqrt{a} \) which gets better and better to any decimal place of our choice as we progress further away from our initial guess using the resulting recursive sequence. Such an ingenious way of computing the square root predates Newton and was known in Mesopotamia (1,500 B.C.) as well as the Greeks ( A.D) [15,16]. Unfortunately, these nameless Babylonian mathematicians and Greeks did not receive credit for their useful fast convergence technique which has successfully been incorporated into programmable calculators or graphing utility and microcomputers as an algorithm for the calculation of the square root of positive real numbers [12,17]. Interestingly enough, by subjecting the simple equation of the form \( x^{2}-a = 0 \) to the Newton-Raphson's method [18], one is led to the sequence type (II) \( u_{n+1} = 1/2(u_{n} + a/u_{n}) \), the precise form of the fixed point intervention explored and used by the Babylonian much earlier than Newton and his compatriots. It is in the light of this coincidence that such an important sequence has come to bear their names instead. We shall demonstrate and prove a general bounded interval that satisfies the convergence criteria for such a sequence using AM-GM relations and the inequality of basic algebra.
The study of nested radicals do not date back into a very distant past, and for what it worth, it was until the 1800s, and in the early 1900s, that mathematicians in that era such as Galois and Ramanujan brought such intriguing continued squares to the center stage [19].
Recurrence relations under a radical sign are best handled using prove by induction [20]. Despite these claims, Ramanujan offers a way of handling such problems and even much more so, on the corridors of analysis, a single radical involving their definition results in a polynomial of degree two, which is easily solved with effortless ease. The situation is quite different, in fact, the level of complexity increases exponentially and becomes more complicated [21] when the radical goes beyond unity. The sequence type (III) falls into this category and hopefully, we shall use the reduced form of a bi-quadratic to determine a general expression to which such a sequence turns to, as one goes infinitely far in the sequence [13].
Besides, the monotone convergence theorem [22,23] is usually invoked and assumed if a limit of a sequence can be determined beforehand, but getting an upper bound or a lower bound is nearly impossible for a monotonically decreasing or increasing sequence. The sequence cannot go pass its infimum or supremum and so depending on the directions to which the terms are gradually clustering toward, the infimum or supremum may pass for its limit of convergence.
3. Analysis and results
The limit of a recursive sequence can easily be developed from a fixed point consideration, that is, by going out far enough in the sequence away from the initial term, the terms of the sequence get sufficiently closer and closer to each other [13]. A fix point equation could be adopted from the defining recursive sequence, however, this does not guarantee convergence. The sufficient and necessary condition needed to conclude convergence is to demonstrate that the sequence is bounded and monotonic.3.1. Prove of convergence for recursive sequence type I
An attempt is made in proving the convergence of the real sequence defined byThe first being that, the quantity \( x = bc/(b-a) \) serves as an equilibrium point with regard to the stability of the sequence type (I). This may play the row of either an upper bound or a lower bound, depending on how the initial pre-defined term \( u_{1} \) is less or greater than it.
Secondly, it is susceptible to the derivation of a closed-form formula for all integral values of \( n \).
Thirdly, since the fraction \( a/b \) is clearly less than unity, it follows that the contraction sequence is convergent.
Now we shall show boundedness and monotonic characterization of the sequence by making the conjecture that
Next, we prove monotonic property for \( u_{n} \) by noting that
3.2. Prove of convergence for recursive sequence type II
Given the sequence for the evaluation of the square root of some general real number '\( a \)' by \[ u_{n+1} = \dfrac{1}{2} \left( u_{n} + \dfrac{a}{u_{n}}\right), \mbox{ where } u_{1} > 0, \, a > 0, \, n \ge 1, \] we show convergence as follows.Firstly, it can be seen that the arithmetic geometric mean of
\[ u_{n+1} = \dfrac{1}{2} \left( u_{n} + \dfrac{a}{u_{n}} \right) \ge \sqrt{a} .\] Since this algorithm evaluates the square root of a positive real number '\( a \)', it is plausible to assert that the root of a number cannot be equal or greater than the number itself except 1. Thus, the choice of an upper bound for the sequence type (II) is taken to be the positive real number '\( a \)' itself and hence we shall claim thatNext, to show that \( u_{n} \) is monotonic non-increasing sequence, we may infer from our claim that
Once \( u_{n} \) meets the litmus test of being monotonic and bounded, it converges to a limit which is exactly the same as its fixed point, thus from the recurrence relation, it is readily shown as
\[ L^{2} -a = 0 \implies L = \pm \sqrt{a} \implies L = \sqrt{a} .\] Observe that the negative fixed point is discarded mainly for two reasons; the first being that the sequence \( u_{n} > 0 \), and secondly, it is outside the defining bound for the sequence \( u_{n} \).3.3. Prove of convergence for recursive sequence type III
To determine the convergence of the nested square root sequence, defined inductively by \[ u_{n+1} = \sqrt{a + \sqrt{u_{n}}}, \mbox{ where } u_{1} = \sqrt{a}, \, a > 2, \, n \ge 1, \] we must show that the sequence is bounded and also posses monotone property. To help achieve this, we first claim and prove that \( u_{n} \) is bounded in the interval \( 0 < u_{n} < a \). By this claim, we must demonstrate that the successive term \( u_{n+1} \) also lies in this bound and satisfies this claim. The implication of such a claim leads to the following inequalitiesNext to show that \( u_{n} \) is monotonic, one may be able to equally write down
Now having shown that \( u_{n} \) is bounded and monotonic, we know the sequence converges to a limit, thus \( \lim\limits_{n \to \infty} u_{n+1} = \lim\limits_{n \to \infty} u_{n} = L \). Eliminating the radicals from the recurrence sequence, we see that the value to which the limit \( L \) of the sequence \( u_{n} \) converges to is satisfied by the equation \( L^{4} - 2 aL^{2} - L + a^{2} = 0 \). To solve this equation, it can be seen that the form of the equation could be expressed as
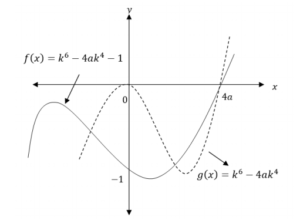
A sketch of the resulting Equation (23) and the approximating polynomial is shown in Figure 1.
Figure 1. Nested fixed point and approximating polynomial
4. Discussion of results
The discussion of the results will be narrowed down to the monotonic property and the pre-defined terms associated with the given sequences under consideration. The choice of the initial point plays the vital row of skewing a sequence to a particular direction in their classification as monotonically increasing or decreasing sequence. For instance, in the case of sequence type I, if the initial point is made bigger than the equilibrium point \( bc/(b-a) \), or on the other hand, if we take the leading term '\( a \)' of the sequence type III as its initial term, it turns out that both sequence types now becomes monotonically decreasing. There is however an exception to this rule, some recursive sequences are not affected by the choice of the initial point. A point in case is sequence type II, that is if we take the initial point to be lesser than the lower bound \( \sqrt{a} \), it will exhibit monotonic increasing behavior for finite consecutive terms of the sequence to a point, but will eventually assume its true characterization as a decreasing sequence in general, for infinitely many terms of that sequence. The underline principle of illustrating that a sequence is monotonic is hinged on comparison and so different approaches that make such conditions achievable were exploited for the various sequence types I, II, and III considered.Finally, another observation worth noting is that sequence type I yielded a closed-form formula, while sequence types II and III did not. This is typical for most sequences due to their intricate nature. Therefore, any attempt to obtain their closed forms could be a waste of effort. Fortunately, with or without a closed-form formula, bit and pieces of qualitative information could be derived from a recurrence sequence and could be equally used to achieve the same purpose as a closed-form formula.
5. Conclusion
In the present study, convergence of the generalization of three types of sequences defined recursively, with special names given as, the first-order difference equation or the arithmetico-geometric sequence, the Newton-Raphson's algorithm, and the nested square root problem are discussed. A strict use of the algebra of inequalities and equations were applied to these recursive sequences to establish convergence. Remarkably, they were in agreement in principle with the use of mathematical induction and other techniques usually applied in proving convergence with respect to recursive sequences. The study clearly falls in line with the monotone convergence theorem and offers an alternative way of establishing boundedness, monotonicity, and convergence in connection with such special sequences.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest
The authors declare no conflict of interest.References
- Almatrafi, M. B. (2019). Solutions structures for some systems of fractional difference equations. Open Journal of Mathematical Analysis, 3(1), 51-61. [Google Scholor]
- Asiri, A., & Elsayed, E. M. (2019). Dynamics and solutions of some recursive sequences of higher order. Journal of Computational Analysis & Applications, 26(1), 656-670. [Google Scholor]
- Elsayed, E. M., & Marwa, M. A. (2020). Expressions and dynamical behavior of rational recursive sequences. Journal of Computational Analysis & Applications, 28(1), 67-78. [Google Scholor]
- Kazenas, S. D. (2020). The Hadamard product and recursively defined sequences. Open Journal of Discrete Applied Mathematics, 3(1), 20 – 24. [Google Scholor]
- Ocalan, O., & Duman, O. (2019). On solutions of the resursive equations \(x_n= \frac{x_{pn}}{x_{pn}}\ \ (p > 0)\) viabonacci-type sequences. Electronic Journal of Mathematical Analysis and Applications, 7(1), 102-115. [Google Scholor]
- Sanbo1, A., & Elsayed, E. M. (2019). Some properties of the solutions of the difference equation \(x_{n+1}=a x_{n}+\dfrac{b x_{n} x_{n-4}}{c x_{n-3}+dx_{n-4}}\). Open Journal of Discrete Applied Mathematics, 2(2), 31-47. [Google Scholor]
- Simsek, D., Esengul, K. P., & Kyzy, I. M. (2019). On the recursive sequence \(x_{n+ 1}= \frac{x_{n-7}}{1+ x_{n-3}}.\) Filomat, 33(5), 1381-1386. [Google Scholor]
- Dyachenko, M., Mukanov, A., & Tikhonov, S. (2019). Uniform convergence of trigonometric series with general monotone coefficients. Canadian Journal of Mathematics, 71(6), 1445-1463. [Google Scholor]
- Levy, B. C. (2020). Convergence and Limit Theorems. In Random Processes with Applications to Circuits and Communications (pp. 79-113). Springer, Cham. [Google Scholor]
- Singh, K., & Modi, K. (2020). Convergence of double cosine series. Kragujevac Journal of Mathematics, 44(3), 443-458. [Google Scholor]
- Yang, J., & Liu, H. (2019). Strong convergence result for solving monotone variational inequalities in Hilbert space. Numerical Algorithms, 80(3), 741-752. [Google Scholor]
- Backhouse, J. K., Horril, P. J. F., & Houldsworth, S. P. T. (1985). Pure Mathematics. Longman Group Ltd, Edinburgh Gate, Harlow, Essex CM20 2JE. England. [Google Scholor]
- Gaughan, E. (1993). Introduction to Analysis. Brooks/Cole Publishing Company, Pacific Grove, California. [Google Scholor]
- Heard, T. J., & Martin, D. R. (1978). Extending Mathematics: A Course in Pure Mathematics to A Level. An 'A' Level Course in Pure Mathematics, Oxford University Press.[Google Scholor]
- Spiegel, M. R. (1974). Schaums outline series of Theory and problems of Advanced Calculus SI. McGraw-Hill, Inc. Singapore. [Google Scholor]
- Wicklin, R. (2016). The Babylonian Method for Finding Square Roots by Hand - the Doo Loop.
https://blogs.sas.com/content/iml/2016/05/16/babylonian-square-roots.html.
- Thomas, G. B., Finney, R. S., & Weir, M. D. (1988). Calculus and Analytic Geometry (9th Edition). Addison Wesley Publishing Company Inc. USA. [Google Scholor]
- Johnson, S. (2015). Square Roots via Newtons Method, MIT Course 18.335.
https://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-006-introduction-to-algorithms-fall-20 11/lecture-videos/MIT6\_006F11\_lec12.pdf
- Rahal, S., & Xantcha, Q. (2017). Introduction to Nested Radicals. Matematiska Institutionnen, Stockhoms Universitet. [Google Scholor]
- Stewart, J. (2003). Calculus Early Transcendentals International Student (edition); Thomson Learning, , Inc.[Google Scholor]
- Sury, B. (2007). Ramanujan’s Route to Roots of Roots. Talk in IIT Madras. [Google Scholor]
- Dutta, H., Natarajan, P. N., & Cho, Y. J. (2019). Concise Introduction to Basic Real Analysis. CRC Press. [Google Scholor]
- Peterson, J. K. (2020). Basic Analysis I: Functions of a Real Variable. CRC Press. [Google Scholor]
- Talbert, J. F., Godman, A., & Ogum, G. E. O. (2009). Additional Mathematics for West Africa. Longman Group UK Ltd. Burnt Mill. Harlow, Essex CM20, England. [Google Scholor]
- Ross, K. (2013). Elementary Analysis: the Theory of Calculus. Springer Science and Business Media. [Google Scholor]