INFORMATION MENU
Open Access Full-Text PDF

Engineering and Applied Science Letters

Vol. 1 (2018), Issue 02, pp. 37–50
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2018.0010

Reverse Zagreb and Reverse Hyper-Zagreb Indices for Silicon Carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\)

Abaid ur Rehman Virk \(^{1}\), Mirza Naveed Jhangeer, M. A. Rehman
Department of Mathematics, University of Management and Technology, Lahore 54000, Pakistan; (A.R.V & M.A.R)
GHS Feroz Pur Chistian, Pakpattan, Pakistan.; (M.N.J)

\(^{1}\)Corresponding Author;  abaid.math@gmail.com

Copyright © 2018 Abaid ur Rehman Virk, Mirza Naveed Jhangeer, M. A. Rehman. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: October 14, 2018 – Accepted: November 10, 2018 – Published: December 31, 2018

Abstract

Topological indices collect information from the graph of molecule and help to predict properties of underlined molecule. Zagreb indices are among the most studied topological indices due to its applications in chemistry. In this report we compute first and second reversed Zagreb indices and first and second reversed Hyper Zagreb indices for \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\). Moreover we also compute first and second reversed Zagreb polynomials and first and second reversed Hyper Zagreb polynomials for \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\).

Index Terms:

Chemical graph theory; Zagreb index; Rendić index; Chemical properties.

1. Introduction

A graph having no loop or multiple edge in known as simple graph. A molecular graph is a simple graph in which atoms and bonds are represented by vertices and edges respectively. The degree of a vertex is the number of edges attached with it. The maximum degree of vertex among the vertices of a graph is denoted by \(\Delta(G)\). Kulli [1] introduces the concept of reverse vertex degree \(c_{v}\), as \(c_{v}=\Delta(G)-d_{g}(v)+1\).
In discrete mathematics, graph theory in general, not only the study of different properties of objects but it also tells us about objects having same properties as investigating object [2]. In particular, graph polynomials related to graph are rich in information [3, 4, 5, 6, 7, 8].
Mathematical tools like polynomials and topological based numbers have significant importance to collect information about properties of chemical compounds [9, 10, 11]. We can find out many hidden information about compounds through theses tools.

Actually, topological indices are numeric quantities that tells us about the whole structure of graph. There are many topological indices [12, 13, 14, 15] that helps us to study physical, chemical reactivities and biological properties. Wiener [16] in 1947, firstly introduce the concept of topological index while working on boiling point. Hosoya polynomial [3] plays an important role in the area of distance-based topological indices. We can find out Wiener index, Hyper Wiener index and Tratch-stankevich-zefirove index from Hosoya polynomial. Rendić index defined by Milan Rendić [17] in 1975 is one of the oldest degree based topological index and have been extensively studied by mathematician and chemists [18, 19, 20, 21, 22]. Later Gutman et al. introduced the first and second Zagreb indices as:

$$M_{1}(G)=\sum_{uv \in E(G)}(d_{u}+d_{v}),$$ $$ M_{2}(G)=\sum_{uv \in E(G)}(d_{u}.d_{v}).$$ Zagreb indices help us in finding \(\pi\)-electronic energy [23]. Many papers [24, 25, 26, 27], surveys [23, 28, 29] and many modification of Zagreb indices are presented in literture [1, 30, 31, 32, 33, 34]. First and second Zagreb polynomials were defined in [7] as: $$M_{1}(G,x)=\sum_{uv \in E(G)}x^{(d_{u}+d_{v})},$$ $$M_{2}(G,x)=\sum_{uv \in E(G)}x^{(d_{u}.d_{v})}.$$ Motivated by these indices, Shirdel et al. [35] proposed the first and second hyper Zagreb indices as: $$H_{1}(G)=\sum_{uv \in E(G)}(d_{u}+d_{v})^{2},$$ $$H_{2}(G)=\sum_{uv \in E(G)}(d_{u}.d_{v})^{2}.$$ The first and second Reverse Zagreb indices [1] are defined as: $$CM_{1}(G)=\sum_{uv \in E(G)}(c_{u}+c_{v}),$$ $$CM_{2}(G)=\sum_{uv \in E(G)}(c_{u}.c_{v}).$$ The first and second Reverse Hyper Zagreb indices [1] are defined as: $$HCM_{1}(G)=\sum_{uv \in E(G)}(c_{u}+c_{v})^{2},$$ $$HCM_{2}(G)=\sum_{uv \in E(G)}(c_{u}.c_{v})^{2}.$$ With the help of reverse Zagreb and hyper Zagreb indices, we now able to define the reverse Zagreb and reverse hyper Zagreb polynomials as: $$CM_{1}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}+c_{v})}, $$ $$CM_{2}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}.c_{v})},$$ and $$HCM_{1}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}+c_{v})^{2}}, $$ $$ HCM_{2}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}.c_{v})^{2}}.$$ Till now there are more than 148 topological indices and non of them complete describe all properties of understudy molecular compound, so there is always room to define new topological indices. Our aim is to study Silicon Carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\). The multiplicative first and second Zagreb indices, multiplicative hyper Zagreb indices, and some other multiplicative degree-based topological indices of \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\) are computed in [36]. Imran et al. in [37] computed the general Rendić and Zagreb types indices, geometric arithmetic index, atom-bond connectivity index, fourth atom-bond connectivity and fifth geometric arithmetic index of \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\). In this report, we aim to compute reversed first and second Zagreb indices, reversed first and second Hyper Zagreb indices, reversed first and second Zagreb polynomials and reversed first and second Hyper Zagreb polynomials for \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II(G).\) Figures of this paper are taken from [36, 37].

2. Silicon Carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\)

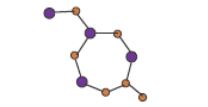
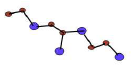
In 1891, an American scientist discover Silicon Carbide. But now a days, we can produce silicon carbide artificially by silica and carbon. Till 1929, silicon carbide was known as the hardest material on earth. Its Mohs hardness rating is 9, which makes this similar to diamond. Here, we will find out reverse zagreb, hyper reverse Zagreb and its polynomials for silicon carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\).

Figure 1. Unit Cell of  \(Si_{2}C_{3}I[r,s]\).

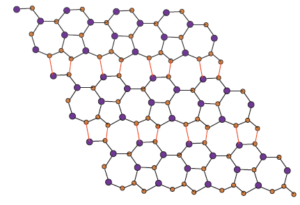
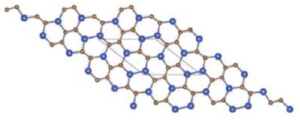
Figure 2. \(Si_{2}C_{3}I[r,s]\) for r = 4, s = 3.

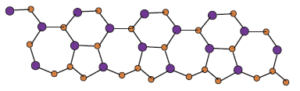
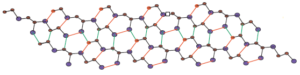
Figure 3. \(Si_{2}C_{3}I[r,s]\) for r = 4, s = 1.

3. Main Results

Here, we will compute reverse Zagreb and reverse hyper Zagreb indices for Silicon Carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\), where \(r\) is the number of connected unit cells, in row (chain) and \(s\) is the number of connected rows each with \(r\) number of cells.

3.1. Silicon Carbide \(Si_{2}C_{3}I[r,s]\)

Theorem 3.1. For the Silicon Carbide \(Si_{2}C_{3}I[r,s]\), the first and second reverse Zagreb indices are:

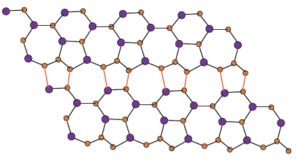
Figure 4. \(Si_{2}C_{3}II[r,s]\) for r = 4, s = 2.

Figure 5. Unit Cell of  \(Si_{2}C_{3}II[r,s]\).

Figure 6. \(Si_{2}C_{3}II[r,s]\)  for r = 3, s = 3.

Figure 7. \(Si_{2}C_{3}II[r,s]\) for r = 5, s = 1.

Figure 8. \(Si_{2}C_{3}II[r,s]\)  for r = 5, s = 2.

  1. \(CM_{1}(Si_{2}C_{3}I[r,s])=30rs+4r+6s-4, \)
  2. \(CM_{2}(Si_{2}C_{3}I[r,s])= 15rs+7r+9s-2. \)

Proof. The vertex and edge set of Silicon Carbide is , \(|V(Si_{2}C_{3}I[r,s])|=10rs\) and \(|E(Si_{2}C_{3}I[r,s])|=15rs-2r-3s\), respectively. From figure[1-4], we can say that, there are five type of edges in \(Si_{2}C_{3}I[r,s]\). The edge set of \(Si_{2}C_{3}I[r,s]\) is portioned into the following five edge sets: $$E_{1}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=1, d_{v}=2\},$$ $$E_{2}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=1, d_{v}=3\},$$ $$E_{3}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=2, d_{v}=2\},$$ $$E_{4}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=2, d_{v}=3\},$$ $$E_{5}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=3, d_{v}=3\},$$ such that, \(|E_{1}(Si_{2}C_{3}I[r,s])|=1\),
\(|E_{2}(Si_{2}C_{3}I[r,s])|=1\),
\(|E_{3}(Si_{2}C_{3}I[r,s])|=r+2s\),
\(|E_{4}(Si_{2}C_{3}I[r,s])|=6r-1+8(s-1) \)
and \(|E_{5}(Si_{2}C_{3}I[r,s])|=15rs-9r-13s+7.\)
As, the maximum degree in \(Si_{2}C_{3}I[r,s]\) is 3, so, $$c_{u}=\Delta(G)-d_{G}(u)+1= 4-d_{G}(u).$$ The reverse edge set of \(Si_{2}C_{3}I[r,s]\) is given as: $$CE_{1}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=3, c_{v}=2\},$$ $$CE_{2}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=3, c_{v}=1\},$$ $$CE_{3}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=2, c_{v}=2\},$$ $$CE_{4}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=2, c_{v}=1\},$$ $$CE_{5}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=1, c_{v}=1\}.$$ And, \(|CE_{1}(Si_{2}C_{3}I[r,s])|=1\),
\(|CE_{2}(Si_{2}C_{3}I[r,s])|=1\),
\(|CE_{3}(Si_{2}C_{3}I[r,s])|=r+2s\),
\( |CE_{4}(Si_{2}C_{3}I[r,s])|=6r-1+8(s-1)\)
and \(|CE_{5}(Si_{2}C_{3}I[r,s])|=15rs-9r-13s+7\).
(1) The first reverse Zagreb index for \(Si_{2}C_{3}I[r,s]\) is: \begin{eqnarray*} CM_{1}(Si_{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})\\ &=&(3+2)(1)+(3+1)(1)+(2+2)(r+2s)+(2+1)\\ & &(6r-1+8(s-1))+(1+1)(15rs-9r-13s+7)\\ &=&30rs+4r+6s-4. \end{eqnarray*} (2) The second reverse Zagreb index for \(Si_{2}C_{3}I[r,s]\) is: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})\\ &=&(3\cdot2)(1)+(3\cdot1)(1)+(2\cdot2)(r+2s)+(2\cdot1)(6r-1\\ & &+8(s-1))+(1\cdot1)(15rs-9r-13s+7)\\ &=&15rs+7r+9s-2. \end{eqnarray*}

Theorem 3.2. The first and second reverse Zagreb polynomials for \(Si_{2}C_{3}I[r,s]\) are:

  1. \(CM_{1}(Si_{2}C_{3}I[r,s],x)=x^{5}+(r+2s+1)x^{4}+(6r-1+8(s-1))x^{3}+(15rs-9r-13s+7)x^{2}, \)
  2. \(CM_{2}(Si_{2}C_{3}I[r,s],x)=x^{6}+(r+2s)x^{4}+x^{3}+(6r-1+8(s-1))x^{2}+(15rs-9r-13s+7)x.\)

Proof. Now, by the reverse edge partitions for \(Si_{2}C_{3}I[r,s]\), we have:
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as: \begin{eqnarray*} CM_{1}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})}\\ &=&(1)x^{(3+2)}+(1)x^{(3+1)}+(r+2s)x^{(2+2)}+(6r-1\\ & &+8(s-1))x^{(2+1)}+(15rs-9r-13s+7)x^{(1+1)}\\ &=&x^{5}+(r+2s+1)x^{4}+(6r-1+8(s-1))x^{3}\\&&+(15rs-9r-13s+7)x^{2}. \end{eqnarray*} (2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})}\\ &=&(1)x^{(3\cdot2)}+(1)x^{(3.1)}+(r+2s)x^{(2\cdot2)}+(6r-1\\ & &+8(s-1))x^{(2\cdot1)}+(15rs-9r-13s+7)x^{(1\cdot1)}\\ &=& x^{6}+(r+2s)x^{4}+x^{3}+(6r-1+8(s-1))x^{2}\\&&+(15rs-9r-13s+7)x. \end{eqnarray*}

Theorem 3.3. The first and second reverse hyper Zagreb indices of Silicon Carbon \(Si_{2}C_{3}I[r,s]\) are:

  1. \(HCM_{1}(Si_{2}C_{3}I[r,s])=60rs+34r+50s-12,\)
  2. \(HCM_{2}(Si_{2}C_{3}I[r,s])=15rs+31r+55s-4.\)

Proof. By reverse edge partition and definition of reverse hyper Zagreb indices, we have:
(1) The first reverse hyper Zagreb index for \(Si_{2}C_{3}I[r,s]\) is: \begin{eqnarray*} CM_{1}(Si _{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})^{2}\\ &=&(3+2)^{2}(1)+(3+1)^{2}(1)+(2+2)^{2}(r+2s)+(2+1)^{2}\\ & &(6r-1+8(s-1))+(1+1)^{2}(15rs-9r-13s+7)\\ &=&60rs+34r+50s-12. \end{eqnarray*} (2) The second reverse hyper Zagreb index for \(Si_{2}C_{3}I[r,s]\) is: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})^{2}\\ &=&(3\cdot2)^{2}(1)+(3\cdot1)^{2}(1)+(2\cdot2)^{2}(r+2s)+(2\cdot1)^{2}\\ & &(6r-1+8(s-1))+(1\cdot1)^{2}(15rs-9r-13s+7)\\ &=&15rs+31r+55s-4. \end{eqnarray*}

Theorem 3.4. The first and second reverse hyper Zagreb polynomials of \(Si_{2}C_{3}$ $I[r,s]\) are:

  1. \(HCM_{1}(Si_{2}C_{3}I[r,s],x)= x^{25}+(r+2s+1)x^{16}+(6r-1+8(s-1))x^{9}+(15rs-9r-13s+7)x^{4}, \)
  2. \(HCM_{1}(Si_{2}C_{3}I[r,s],x)= x^{36}+(r+2s)x^{16}+x^{9}+(6r-1+8(s-1))x^{4}+(15rs-9r-13s+7)x.\)

Proof. Now, by the reverse edge partitions for \(Si_{2}C_{3}I[r,s]\), we have
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as: \begin{eqnarray*} HCM_{1}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})^{2}}\\ &=&(1)x^{(3+2)^{2}}+(1)x^{(3+1)^{2}}+(r+2s)x^{(2+2)^{2}}+(6r-1\\ & &+8(s-1))x^{(2+1)^{2}}+(15rs-9r-13s+7)x^{(1+1)^{2}}\\ &=&x^{25}+(r+2s+1)x^{16}+(6r-1+8(s-1))x^{9}\\&&+(15rs-9r-13s+7)x^{4}. \end{eqnarray*} (2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as: \begin{eqnarray*} HCM_{2}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})^{2}}\\ &=&(1)x^{(3\cdot2)^{2}}+(1)x^{(3\cdot1)^{2}}+(r+2s)x^{(2\cdot2)^{2}}+(6r-1\\ & &+8(s-1))x^{(2\cdot1)^{2}}+(15rs-9r-13s+7)x^{(1\cdot1)^{2}}\\ &=& x^{36}+(r+2s)x^{16}+x^{9}+(6r-1+8(s-1))x^{4}\\&&+(15rs-9r-13s+7)x. \end{eqnarray*}

In the following Table 1, we computed first and second reverse Zagreb and first and second reverse hyper Zagreb indices for \(Si_{2}C_{3}I[r,s]\) for specific values of \(r\) and \(s\).

Table 1. first and second reverse Zagreb and first and second reverse hyper Zagreb indices for \(Si_{2}C_{3}I[r,s]\) for specific values of \(r\) and \(s\)

\(r=1,s=1\) \(r=1,s=2\) \(r=2,s=1\) \(r=2,s=1\) \(r=2,s=3\) \(r=3,s=3\)
\(CM_{2}\) 36 72 70 136 202 296
\(CM_{2}\) 29 53 51 90 129 181
\(HCM_{2}\) 132 242 226 396 566 780
\(HCM_{2}\) 97 167 143 228 313 389

3.2. Silicon Carbide \(Si_{2}C_{3}II[r,s]\)

Theorem 3.5. For the Silicon Carbide \(Si_{2}C_{3}II[r,s]\), the first and second reverse Zagreb indices are:

  1. \(CM_{1}(Si_{2}C_{3}II[r,s])=30rs+6r+6s-6 ,\)
  2. \(CM_{2}(Si_{2}C_{3}II[r,s])= 15rs+11r+11s-2. \)

Proof. The vertex and edge set of Silicon Carbide is, \(|V(Si_{2}C_{3}II[r,s])|=10rs\) and \(|E(Si_{2}C_{3}II[r,s])|=15rs-2r-3s\), respectively. From the Figures 5-8, we can observe that, there are five type of edges in \(Si_{2}C_{3}II[r,s]\). The edge set of \(Si_{2}C_{3}II[r,s]\) is portioned into following five edge sets: $$E_{1}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=1, d_{v}=2\},$$ $$E_{2}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=1, d_{v}=3\},$$ $$E_{3}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=2, d_{v}=2\},$$ $$E_{4}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=2, d_{v}=3\},$$ $$E_{5}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=3, d_{v}=3\},$$ such that, \(|E_{1}(Si_{2}C_{3}II[r,s])|=2\),
\( |E_{2}(Si_{2}C_{3}II[r,s])|=1\),
\(|E_{3}(Si_{2}C_{3}II[r,s])|=2r+2s\),
\(|E_{4}(Si_{2}C_{3}II[r,s])|=8r+8s-14\)
and \(|E_{5}(Si_{2}C_{3}II[r,s])|=15rs-13r-13s+11.\)
The maximum vertex degree \(Si_{2}C_{3}II[r,s]\) is 3, so, $$c_{u}=\Delta(G)-d_{G}(u)+1= 4-d_{G}(u).$$ The reverse edge set of \(Si_{2}C_{3}II[r,s]\) is given as: $$CE_{1}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=3, c_{v}=2\},$$ $$CE_{2}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=3, c_{v}=1\},$$ $$CE_{3}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=2, c_{v}=2\},$$ $$CE_{4}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=2, c_{v}=1\},$$ $$CE_{5}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=1, c_{v}=1\},$$ and we have, \(|E_{1}(Si_{2}C_{3}II[r,s])|=2\),
\(|E_{2}(Si_{2}C_{3}II[r,s])|=1\),
\( |E_{3}(Si_{2}C_{3}II[r,s])|=2r+2s\),
\(|E_{4}(Si_{2}C_{3}II[r,s])|=8r+8s-14\)
and \(|E_{5}(Si_{2}C_{3}II[r,s])|=15rs-13r-13s+11\).
(1) The first reverse Zagreb index for \(Si_{2}C_{3}II[r,s]\) is: \begin{eqnarray*} CM_{1}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})\\ &=&(3+2)(2)+(3+1)(1)+(2+2)(2r+2s)+(2+1)\\ & &(8r+8s-14)+(1+1)(15rs-13r-13s+11)\\ &=&30rs+6r+6s-6. \end{eqnarray*} (2) The second reverse Zagreb index for \(Si_{2}C_{3}II[r,s]\) is: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})\\ &=&(3\cdot2)(2)+(3\cdot1)(1)+(2\cdot2)(2r+2s)+(2\cdot1)\\ & &(8r+8s-14)+(1\cdot1)(15rs-13r-13s+11)\\ &=&15rs+11r+11s-2. \end{eqnarray*}

Theorem 3.6. The first and second reverse Zagreb polynomials for \(Si_{2}C_{3}II[r,s]\) are:

  1. \(CM_{1}(Si_{2}C_{3}II[r,s],x)= x^{5}+(2r+2s+1)x^{4}+(8r+8s-14)x^{3}+(15rs-9r-13s+7)x^{2},\)
  2. \(CM_{2}(Si_{2}C_{3}II[r,s],x)=2x^{6}+(2r+2s)x^{4}+x^{3}+(8r+8s=14)x^{2}+(15rs-13r-13s+11)x.\)

Proof. Now, by the reverse edge partitions for \(Si_{2}C_{3}II[r,s]\), we have:
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}II[r,s]\), is given as: \begin{eqnarray*} CM_{1}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})}\\ &=&(2)x^{(3+2)}+(1)x^{(3+1)}+(2r+2s)x^{(2+2)}+(8r\\ & &+8s-14)x^{(2+1)}+(15rs-13r-13s+11)x^{(1+1)}\\ &=&x^{5}+(2r+2s+1)x^{4}+(8r+8s-14)x^{3}\\&&+(15rs-9r-13s+7)x^{2}. \end{eqnarray*} (2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}II[r,s]\), is given as: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})}\\ &=&(2)x^{(3\cdot2)}+(1)x^{(3\cdot1)}+(2r+2s)x^{(2\cdot2)}+(8r\\ & &+8s-14)x^{(2\cdot1)}+(15rs-13r-13s+11)x^{(1.\cdot1)}\\ &=& 2x^{6}+(2r+2s)x^{4}+x^{3}+(8r+8s-14)x^{2}\\&&+(15rs-13r-13s+11)x. \end{eqnarray*}

Theorem 3.7. The first and second reverse Hyper Zagreb indices of Silicon Carbon \(Si_{2}C_{3}II[r,s]\) are:

  1. \(HCM_{1}(Si_{2}C_{3}II[r,s])=60rs+51r+51s-16,\)
  2. \(HCM_{2}(Si_{2}C_{3}II[r,s])=15rs+51r+51s+108.\)

Proof. By reverse edge partition and definition of reverse hyper Zagreb indices, we have:
(1) The first reverse Hyper Zagreb index for \(Si_{2}C_{3}II[r,s]\) is: \begin{eqnarray*} CM_{1}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})^{2}\\ &=&(3+2)^{2}(2)+(3+1)^{2}(1)+(2+2)^{2}(2r+2s)+(2+1)^{2}\\ & &(8r+8s-14)+(1+1)^{2}(15rs-13r-13s+11)\\ &=&60rs+52r+52s-16. \end{eqnarray*} (2) The second reverse Hyper Zagreb index for \(Si_{2}C_{3}I[r,s]\) is: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})^{2}\\ &=&(3+2)^{2}(2)+(3+1)^{2}(1)+(2+2)^{2}(2r+2s)\\ & &+(2+1)^{2}(8r+8s-14)+(1+1)^{2}(15rs\\&&-13r-13s+11)\\ &=&15rs+51r+51s+108. \end{eqnarray*}

Theorem 3.8. The first and second reverse hyper Zagreb polynomials of \(Si_{2}C_{3}$ $II[r,s]\) is:

  1. \(HCM_{1}(Si_{2}C_{3}II[r,s],x)= 2x^{25}+(2r+2s+1)x^{16}+(8r+8s-14)x^{9}+(15rs-13r-13s+11)x^{4}, \)
  2. \(HCM_{1}(Si_{2}C_{3}II[r,s],x)= 2x^{36}+(2r+2s)x^{16}+x^{9}+(8r+8s-14)x^{4}+(15rs-13r-13s+11)x.\)

Proof. Now, by the reverse edge partitions for \(Si_{2}C_{3}II[r,s]\), we have:
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}II[r,s]\), is given as: \begin{eqnarray*} CM_{1}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})^{2}}\\ &=&(2)x^{(3+2)^{2}}+(1)x^{(3+1)^{2}}+(2r+2s)x^{(2+2)^{2}}+(8r\\ & &+8s-14)x^{(2+1)^{2}}+(15rs-13r-13s+11)x^{(1+1)^{2}}\\ &=&2x^{25}+(2r+2s+1)x^{16}+(8r+8s-14)x^{9}\\&&+(15rs-13r-13s+11)x^{4}. \end{eqnarray*} (2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as: \begin{eqnarray*} CM_{2}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})^{2}}\\ &=&(2)x^{(3\cdot2)^{2}}+(1)x^{(3\cdot1)^{2}}+(2r+2s)x^{(2\cdot2)^{2}}+(8r+8s\\ & &-14)x^{(2\cdot1)^{2}}+(15rs-13r-13s+11)x^{(1\cdot1)^{2}}\\ &=&2x^{36}+(2r+2s)x^{16}+x^{9}+(8r+8s-14)x^{4}\\&&+(15rs-13r-13s+11)x. \end{eqnarray*}

In the following Table 2, we computed first and second reverse Zagreb and first and second reverse Hyper Zagreb indices for \(Si_{2}C_{3}II[r,s]\) for spefic values of \(r\) and \(s\).

Table 2. first and second reverse Zagreb and first and second reverse Hyper Zagreb indices for \(Si_{2}C_{3}II[r,s]\) for spefic values of \(r\) and \(s\)

\(r=1,s=1\) \(r=1,s=2\) \(r=2,s=1\) \(r=2,s=1\) \(r=2,s=3\) \(r=3,s=3\)
\(CM_{2}\) 36 72 72 138 204 300
\(CM_{2}\) 35 61 61 162 143 199
\(HCM_{2}\) 146 257 257 428 599 830
\(HCM_{2}\) 225 291 291 372 453 549

Conclusion

\noindent The first and second Zagreb indices are used to compute total \(\pi\)-energy of conjugated molecules. These indices are also useful in the study of anti-inflammatory activities of certain chemical instances, and in elsewhere. In this paper we have obtained reverse Zagreb indices, hyper reverse Zagreb indices and their polynomials for Silicon Carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}I[r,s]\).

Competing Interests

The authors declare that they have no competing interests.

References

  1. Kulli, V. R. (2018). Reverse Zagreb and reverse hyper-Zagreb indices and their polynomials of rhombus silicate networks. Annals of Pure and Applied Mathematics, 16(1), 47-51. [Google Scholor]
  2. West, D. B. (2001). Introduction to graph theory (Vol. 2). Upper Saddle River: Prentice hall. [Google Scholor]
  3. Hosoya, H. (1988). On some counting polynomials in chemistry. Discrete Applied Mathematics, 19(1-3), 239-257. [Google Scholor]
  4. Siddiqui, M. K., Imran, M., & Ahmad, A. (2016). On Zagreb indices, Zagreb polynomials of some nanostar dendrimers. Applied Mathematics and Computation, 280, 132-139. [Google Scholor]
  5. Deutsch, E., & Klavžar, S. (2014). M-polynomial and degree-based topological indices. arXiv preprint arXiv:1407.1592. [Google Scholor]
  6. Munir, M., Nazeer, W., Rafique, S., & Kang, S. M. (2016). M-polynomial and degree-based topological indices of polyhex nanotubes. Symmetry, 8(12), 149. [Google Scholor]
  7. Fath-Tabar, G. (2009). Zagreb polynomial and pi indices of some nano structures. Digest Journal of Nanomaterials and Biostructures, 4(1), 189 - 191 [Google Scholor]
  8. Iranmanesh, M., & Saheli, M. (2015). On the harmonic index and harmonic polynomial of Caterpillars with diameter four. Iranian Journal of Mathematical Chemistry, 6(1), 41-49. [Google Scholor]
  9. Devillers, J., & Balaban, A. T. (Eds.). (2000). Topological indices and related descriptors in QSAR and QSPAR. CRC Press. [Google Scholor]
  10. Karelson, M. (2000). Molecular descriptors in QSAR/QSPR. Wiley-Interscience. [Google Scholor]
  11. Karelson, M., Lobanov, V. S., & Katritzky, A. R. (1996). Quantum-chemical descriptors in QSAR/QSPR studies. Chemical reviews, 96(3), 1027-1044.[Google Scholor]
  12. Bashir, Y., Aslam, A., Kamran, M., Qureshi, M. I., Jahangir, A., Rafiq, M., ... & Muhammad, N. (2017). On forgotten topological indices of some dendrimers structure. Molecules, 22(6), 867. [Google Scholor]
  13. Aslam, A., Guirao, J. L., Ahmad, S., & Gao, W. (2017). Topological indices of the line graph of subdivision graph of complete bipartite graphs. Appl. Math. Inf. Sci., 11(6), 1631-1636.[Google Scholor]
  14. Aslam, A., Ahmad, S., & Gao, W. (2017). On certain topological indices of boron triangular nanotubes. Zeitschrift für Naturforschung A, 72(8), 711-716. [Google Scholor]
  15. Kang, S., Iqbal, Z., Ishaq, M., Sarfraz, R., Aslam, A., & Nazeer, W. (2018). On eccentricity-based topological indices and polynomials of phosphorus-containing dendrimers. Symmetry, 10(7), 237. [Google Scholor]
  16. Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20. [Google Scholor]
  17. Randic, M. (1975). Characterization of molecular branching. Journal of the American Chemical Society, 97(23), 6609-6615. [Google Scholor]
  18. Li, X., & Shi, Y. (2008). A survey on the Randic index. MATCH Commun. Math. Comput. Chem., 59(1), 127-156.[Google Scholor]
  19. Hu, Y., Li, X., Shi, Y., Xu, T., & Gutman, I. (2005). On molecular graphs with smallest and greatest zeroth-order general Randic index. MATCH Commun. Math. Comput. Chem., 54(2), 425-434.[Google Scholor]
  20. Li, X., & Yang, Y. (2004). Sharp bounds for the general Randic index. MATCH Commun. Math. Comput. Chem., 51, 155-166. [Google Scholor]
  21. Clark, L. H., & Moon, J. W. (2000). On the general Randic index for certain families of trees. Ars Combinatoria, 54, 223-235.[Google Scholor]
  22. Hu, Y., Li, X., & Yuan, Y. (2004). Trees with minimum general Randic index.MATCH Commun. Math. Comput. Chem., 52, 119-128. [Google Scholor]
  23. Gutman, I., & Das, K. C. (2004). The first Zagreb index 30 years after. MATCH Commun. Math. Comput. Chem., 50(1), 83-92.[Google Scholor]
  24. Gutman, I. (2014). An exceptional property of first Zagreb index. MATCH Commun. Math. Comput. Chem., 72(3), 733-740. [Google Scholor]
  25. Hosamani, S. M., & Basavanagoud, B. (2015). New upper bounds for the first Zagreb index.MATCH Commun. Math. Comput. Chem., 74(1), 97-101. [Google Scholor]
  26. Das, K. C., & Gutman, I. (2004). Some properties of the second Zagreb index. MATCH Commun. Math. Comput. Chem., 52(1), 3-1. [Google Scholor]
  27. Zhou, B., & Gutman, I. (2005). Further properties of Zagreb indices.MATCH Commun. Math. Comput. Chem., 54, 233-239. [Google Scholor]
  28. Zhou, B. (2004). Zagreb indices. MATCH Commun. Math. Comput. Chem., (52), 113-118.[Google Scholor]
  29. Khalifeh, M. H., Yousefi-Azari, H., & Ashrafi, A. R. (2009). The first and second Zagreb indices of some graph operations. Discrete Applied Mathematics, 157(4), 804-811.[Google Scholor]
  30. Miličević, A., Nikolić, S., & Trinajstić, N. (2004). On reformulated Zagreb indices. Molecular diversity, 8(4), 393-399. [Google Scholor]
  31. Eliasi, M., Iranmanesh, A., & Gutman, I. (2012). Multiplicative versions of first Zagreb index.MATCH Commun. Math. Comput. Chem., 68(1), 217. [Google Scholor]
  32. Hao, J. (2011). Theorems about Zagreb indices and modified Zagreb indices. MATCH Commun. Math. Comput. Chem., 65, 659-670. [Google Scholor]
  33. Kulli, V. R. (2016). Multiplicative Hyper-Zagreb Indices And Coindices Of Graphs: Computing These Indices Of Some Nanostructures. International Research Journal of Pure Algebra , 6(7).[Google Scholor]
  34. Kwun, Y. C., A. R. Virk., Nazeer, W., & Kang, S. M. (2018). On the Multiplicative Degree-Based Topological Indices of Silicon-Carbon \(Si2C3-I [p, q]\) and \(Si2C3-II [p, q].\), Symmetry, 10(8), 320; [Google Scholor]
  35. Shirdel, G. H., Rezapour, H., & Sayadi, A. M. (2013). The hyper-Zagreb index of graph operations. Iranian Journal of Mathematical Chemistry, 4(2), 213-220. [Google Scholor]
  36. Gao, W., Jamil, M. K., & Farahani, M. R. (2017). The hyper-Zagreb index and some graph operations. Journal of Applied Mathematics and Computing, 54(1-2), 263-275.[Google Scholor]
  37. Imran, M., Siddiqui, M. K., Naeem, M., & Iqbal, M. A. (2018). On Topological Properties of Symmetric Chemical Structures. Symmetry, 10(5), 173.[Google Scholor]
Category: EASL - Vol 1 - Issue 2 (2018)