Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2019.0018
Magnetohydrodynamic flow of dissipative casson-carreau nanofluid over a stretching sheet embedded in a porous medium under the influence of thermal radiation and variable internal heat generation
Gbeminiyi Sobamowo\(^1\), O. A. Adesina, Lawrence Jayesimi
Department of Mechanical Engineering, University of Lagos, Akoka, Lagos, Nigeria.; (G.S)
Department of Mechanical Engineering, Yaba College of Technology, Lagos, Nigeria.; (O.A.A)
Works and Physical Planning Department, University of Lagos, Akoka, Lagos, Nigeria.; (L.J)
Abstract
Keywords:
1. Introduction
The roles and importance of thermal radiation are evident in solar power technology, nuclear plants, propulsion devices for aircraft, combustion chambers, glass production, furnace design, and space technology applications, such as comical flight aerodynamics rocket, space vehicles, propulsion systems, plasma physics in the flow structure of atomic plants, combustion processes, internal combustion engines, ship compressors, solar radiations and in chemical processes and space craft re-entry aerodynamics which operates at high temperatures. Also, there are various engineering and industrial applications of magnetohydrodynamic (MHD) fluid behavior such as in the design of cooling system with liquid metals, accelerators, MHD generators, nuclear reactor, pumps, flow meters, study of crystal growth, metal casting, liquid metal cooling blankets for fusion reactors and blood flow. Additionally, recent research works in the past few decades have shown that the study of flow of non-Newtonian materials is a topic of great interest amongst the recent workers in the study of fluid dynamics. The flow applications of non-Newtonian fluids such as blood transport in micro-circulatory system, printer ink, paints, liquid detergents, multi grade oil, polymers, sauce, mud, apple sauce are evident in polymer devolatisation and processing, bubble absorptions, fermentation, plastic foam processing, bubble columns, composite processing, wire and fiber coating, heat exchangers, extrusion process, chemical processing equipment, etc. Also, the analysis of stretched flow with heat transfer is very significant in controlling the quality of the end product in the afore-mentioned areas of applications. Such processes have great dependence on the stretching and cooling rates [1]. Consequently, in the past few years, research efforts have been directed towards the analysis of this very important phenomenon of wide areas of applications. Moreover, the promising significance of magnetohydrodynamics (MHD) fluid behavior in various engineering and industrial applications (such as in the design of cooling system with liquid metals, accelerators, MHD generators, nuclear reactor, pumps, flow meters, study of crystal growth, metal casting, liquid metal cooling blankets for fusion reactors and blood flow) still provokes the continuous studies and interests of researchers.
Additionally, the study of thermal radiation is important in solar power technology, nuclear plants, and propulsion devices for aircraft, combustion chambers, glass production and furnace design, and also in space technology applications, such as comical flight aerodynamics rocket, space vehicles, propulsion systems, plasma physics in the flow structure of atomic plants, combustion processes, internal combustion engines, ship compressors, solar radiations and in chemical processes and space craft re-entry aerodynamics which operates at high temperatures. Therefore, the influences of external factors such as magnetic field and thermal radiation on the flow and heat transfer problem of Newtonian and non-Newtonian fluid have been widely analyzed in recent times. In an early study, MHD fluid flow over a stretching surface was carried out by Anderson et al. [2, 3]. The effect of unsteadiness parameter on the film thickness has been studied [2] and the effect of magnetic field on the flow characteristics of the fluid were explored numerically [3]. Few years later, Chen [4] investigated the power-law fluid film flow of unsteady heat transfer stretching sheet while Dandapat et al. [5, 6] analyzed the effect of variable viscosity and thermo- capillarity on the heat transfer of liquid film flow over a stretching sheet. Meanwhile, Wang [7] developed an analytical solution for the momentum and heat transfer of liquid film flow over a stretching surface. Also, Chen [8] and Sajid et al. [9] investigated the flow characteristics of a non-Newtonian thin film over an unsteady stretching surface considering viscous dissipation using homotopy analysis and homotopy perturbation methods. After a year, Dandapat et al. [10] presented the analysis of two-dimensional liquid film flow over an unsteady stretching sheet while in the same year, effect of power-law index on unsteady stretching sheet was studied by Abbasbandy et al. [11]. Santra and Dandapat [12] numerically studied the flow of the liquid film over an unsteady horizontal stretching sheet. A numerical approach was also used by Sajid et al. [13] to analyze the micropolar film flow over an inclined plate, moving belt and vertical cylinder. A year later, Noor and Hashim [14]1 investigated the effect of magnetic field and thermocapillarity on an unsteady flow of a liquid film over a stretching sheet while Dandapat and Chakraborty [15]) and Dandapat and Singh [16] presented the thin film flow analysis over a non-linear stretching surface with the effect of transverse magnetic field. Heat transfer characteristics of the thin film flows considering the different channels have also been analyzed by Abdel-Rahman [17], Khan et al. [18], Liu et al. [19] and Vajaravelu et al. [20] Meanwhile, Liu and Megahad [21] used homotopy perturbation method to analyze thin film flow and heat transfer over an unsteady stretching sheet with internal heating and variable heat flux. Effect of thermal radiation and thermocapillarity on the heat transfer thin film flow over a stretching surface was examined by Aziz et al. [22]. In their study on the numerical simulation of Eyring-Powell flow and unsteady heat transfer of a laminar liquid film over a stretching sheet using finite difference method, Khader and Megahed [23] established that increasing the Prandtl number reduces the temperature field across the thin film. Vajravelu et al. [24] analyzed the convective heat transfer over a stretching surface with applied magnetic field while Pop and Na [25] studied the influence of magnetic field flow over a stretching permeable surface. In another study, Xu et al. [26] presented a series solutions of the unsteady three-dimensional MHD flow and heat transfer over an impulsively stretching plate. Nazar et al. [27] examined the hydro magnetic flow and heat transfer over a vertically stretched sheet. The effect of MHD stagnation point flow towards a stretching sheet was investigated by Ishak et al. [28] while the influence of thermal radiation on heat transfer in an electrically conducting fluid at stretching surface was explored by Emad [29].
Also, Reddy [30] studied the thermal radiation boundary layer flow of a nanofluid past a stretching sheet under applied magnetic field. Effects of thermal radiation on convective heat transfer in an electrically conducting fluid over a stretching surface with variable viscosity and uniform free stream was examined by Abo-Eldahab and Elgendy [31]. In a recent study, Gnaneswara Reddy [32] investigated the thermal radiation and chemical reaction effects on MHD mixed convective boundary layer slip flow in a porous medium with heat source and Ohmic heating. In another study, Gnaneswara Reddy [33] studied the influence of thermophoresis, Viscous Dissipation and Joule Heating on Steady MHD Flow over an Inclined Radiative Isothermal Permeable Surface. The effect of thermal radiation on magnetohydrodynamics flow was examined by Raptis et al. [34] while Seddeek [35] investigated the impacts of thermal radiation and variable viscosity on magnetohydrodynamics in free convection flow over a semi-infinite flat plate. In another study, Mehmood et al. [36] analyzed unsteady stretched flow of Maxwell fluid in presence of nonlinear thermal radiation and convective condition. Hayat et al. [37] addressed the effects of nonlinear thermal radiation and magnetohydrodynamics on viscoelastic nanofluid flow. Effects of nonlinear thermal radiation on stagnation point flow Farooq et al. [38]. Also, Shehzad et al. [39] presented a study o MHD three-dimensional flow of Jeffrey nanofluid with internal heat generation and thermal radiation. In a recent study, Lin et al. [40] examined the effect of MHD pseudo-plastic nanofluid flow and heat transfer film flow over a stretching sheet with internal heat generation. Numerically, Raju and Sandeep [41] studied heat and mass transfer in MHD non-Newtonian flow while Tawade et al. [42] presented the unsteady flow and heat transfer of thin film over a stretching surface in the presence of thermal radiation, internal heating in the presence of magnetic field. Heat and mass transfer of MHD flows through different channels have been analyzed [43, 44, 45, 46, 47, 48]. Makinde and Animasaun [49] investigated the effect of cross diffusion on MHD bioconvection flow over a horizontal surface. In another study, Makinde and Animasaun [50] presented the MHD nanofluid on bioconvection flow of a paraboloid revolution with nonlinear thermal radiation and chemical reaction while Sandeep [51], Reddy et al. [52] and Ali et al. [53] studied the heat transfer behaviour of MHD flows. Maity et al. [54] analyzed thermocapillary flow of a thin Nanoliquid film over an unsteady stretching sheet.
The above studies have been the consequent of the various industrial and engineering applications of non-Newtonian fluids. Among the classes of non-Newtonian fluids, Carreau fluid which its rheological expressions were first introduced by Carreau [55], is one of the non-Newtonian fluids that its model is substantial for gooey, high and low shear rates [56]. On account of this headway, it has profited in numerous innovative and assembling streams [56]. Owing to these applications, different studies have been carried out to explore the characteristics of Carreau liquid in flow under different conditions. Kumar et al. [40] applied Runge-Kutta and Newton's method to analyze the flow and heat transfer of electrically conducting liquid film flow of Carreau nanofluid over a stretching sheet by considering the aligned magnetic field in the presence of space and temperature dependent heat source/sink, viscous dissipation and thermal radiation. Hayat et al. [57] studied the influence of induced magnetic field and heat transfer on peristaltic transport of a Carreau fluid. Olajuwon [58] presented a study on MHD flow of Carreau liquid over vertical porous plate with thermal radiation. Hayat et al. [59] investigated the convectively heated flow of Carreau fluid while in the same year, Akbar et al. [60] analyzed the stagnation point flow of Carreau fluid. Also, Akbar [61] presented blood flow of Carreau fluid in a tapered artery with mixed convection. A year later, Mekheimer [62] investigated the unsteady flow of a carreau fluid through inclined catheterized arteries haveing a balloon with time-variant overlapping stenosis. Elmaboud et al. [63] developed series solution of a natural convection flow for a Carreau fluid in a vertical channel with peristalsis. Using a revised model, flow of Carreaunanoliquid in the presence of zero mass flux condition at the stretching sheet has been examined by Hashim and Khan [64]. The MHD flow of Carreau fluid with thermal radiation and cross diffusion effects was investigated by Machireddy and Naramgari [65]. Sulochana et al. [66] provided an analysis of magnetohydrodynamic stagnation-point flow of a Carreau nanofluid.
Another non-Newtonian fluid is Casson fluid. Casson fluid is a non-Newtonian fluid first invented by Casson in 1959 [67]. It is a shear thinning liquid which is assumed to have an infinite viscosity at zero rate of shear, a yield stress below which no flow occurs, and a zero viscosity at an infinite rate of shear [68, 69]. If yield stress is greater than the shear stress then it acts as a solid, whereas if yield stress lesser than the shear stress is applied then the fluid would start to move. The fluid is based on the structure of liquid phase and interactive behaviour of solid of a two-phase suspension. It is able to capture complex rheological properties of a fluid, unlike other simplified models like the power law [70] and second, third or fourth-grade models [71]. Some examples of Casson fluid are Jelly, honey, tomato sauce and concentrated fruit juices. Human blood is also treated as a Casson fluid in the presence of several substances such as fibrinogen, globulin in aqueous base plasma, protein, and human red blood cells. Concentrated fluids like sauces, honey, juices, blood, and printing inks can be well described using this model. It has various applications in fibrinogen, cancer homeo-therapy, protein and red blood cells form a chain type structure. Due to these applications many researchers are concentrating characteristics of Casson fluid. Application of Casson fluid for flow between two rotating cylinders is performed in [72]. The effect of magnetohydrodynamic (MHD) Casson fluid flow in a lateral direction past linear stretching sheet was explained by Nadeem et al. [73].
Numerical methods such as Euler and Runge--Kutta methods are limited to solving initial value problems. With the aid of shooting method, the methods could be carried out iteratively to solve boundary value problems. However, these numerical methods are only useful for solving ordinary differential equations i.e. differential equations with a single independent variable. On the other hand, numerical methods such as finite difference method (FDM), finite element methods (FEM) and finite volume method (FVM) can be adopted solve differential equations with single and multiple independent variables as they have been used to different linear and non-linear differential equations in literatures. The numerical solution of FDM represents an efficient way of obtaining temperature profile for the steady heat transfer processes. The FDM can be used for solving any complex body by breaking the body into small domains. Also, choice of finer grids which requires high computing capability can remove approximation errors to larger extent. Hence, in this work, finite difference method. Therefore, in this study, finite difference method is applied to analyze the combined influences of thermal radiation, inclined magnetic field and temperature-dependent internal heat generation on unsteady two-dimensional flow and heat transfer analysis of dissipative Casson-Carreau nanofluid over a stretching sheet embedded in a porous medium are examined. Using kerosene as the base fluid embedded with the silver (Ag) and copper (Cu) nanoparticles, the effects of other pertinent parameters on flow and heat transfer characteristics of the nanofluids are investigated and discussed.
2. Problem Formulation
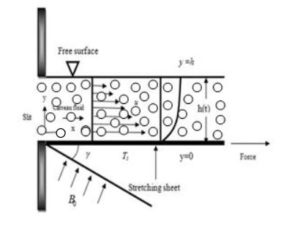
Consider an unsteady, two-dimensional boundary layer flow of an electrically conducting and heat generating Casson and Carreau nanofluids over a stretching sheet bounded by a thin liquid film of uniform thickness \(h(t)\) over a horizontal elastic sheet which emerges from a narrow slit at the origin of the cartesian coordinate system which is schematically represented in Figure 1. The sheet is stretched along the x-axis with stretching velocity \(U(x,t)\) and y--axis is normal to it. An inclined magnetic field. The effects of non-uniform heat source/sink, thermal radiation, viscous is applied to the stretching sheet at angle dissipation and volume fraction are taken into consideration.Figure 1. Flow geometry of the problem.
The non-uniform heat generation/absorption \(q'''\) is taken as
Method of Solution
Equations (21) and (22) are systems of coupled non-linear ordinary differential equations which are to be solved by using the boundary conditions (24). The exact solution is not possible for this set of equations. The use and the accuracy of finite difference method for the analysis of nonlinear problems has earlier been pointed out by Han et al. (2005). Therefore, in this work, finite difference method is used to discretize the governing Equation (17) combined with the boundary conditions of Equation (19). The finite difference forms or schemes for each differential in the governing differential equations are given as\(f''''=\frac{2f_{i+1} -9f_{i} +16f_{i-1} -14f_{i-2} +6f_{i-3} -f_{i-4} }{\left(\Delta \eta \right)^{4} } \)
\(f'''=\frac{3f_{i+1} -10f_{i} +12f_{i-1} -6f_{i-2} +f_{i-3} }{2\left(\Delta \eta \right)^{3} } \)
\(f''=\frac{f_{i+1} -2f_{i} -f_{i-1} }{\left(\Delta \eta \right)^{2} } \)
\(f'=\frac{f_{i+1} -f_{i-1} }{2\left(\Delta \eta \right)} =\frac{f_{i+1} -f_{i} }{\Delta \eta } =\frac{f_{i} -f_{i-1} }{\Delta \eta } \)
\(\theta ''=\frac{\theta _{i+1} -2\theta _{i} -\theta _{i-1} }{\left(\Delta \eta \right)^{2} } \)
\(\theta '=\frac{\theta _{i+1} -\theta _{i-1} }{2\left(\Delta \eta \right)} =\frac{\theta _{i+1} -\theta _{i} }{\Delta \eta } =\frac{\theta _{i} -\theta _{i-1} }{\Delta \eta } \)
Substituting the above finite difference schemes into Equations (21) and (22), one obtains an equivalent finite difference schemes as
4. Results and discussion
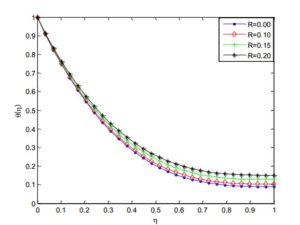
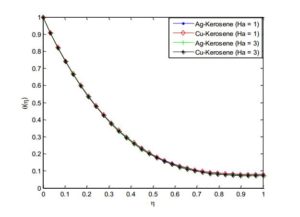
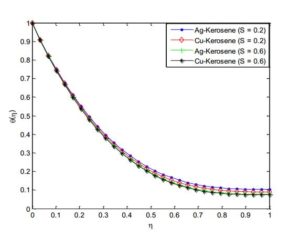
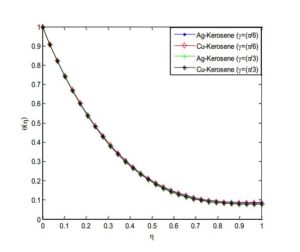
For the computational domain, numerical solutions are computed and grid-independence study is made in order to obtain the results accurately. The necessary convergence of the results is achieved with the desired degree of accuracy. The results with the discussion are illustrated through the Figures 2-21 to substantiate the applicability of the present analysis. The influence of pertinent parameters such as magnetic field parameter, unsteadiness parameter, heat source/sink parameter, Eckert number, volume fraction of nanoparticles etc. on the flow and heat transfer of the thin film flow are investigated.Figure 2. Effects of radiation parameter on the temperature profile of Ag-Kerosene Casson-Carreau nanofluid
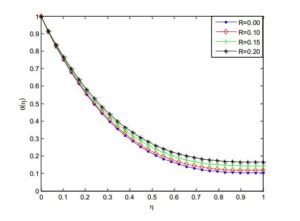
Figure 3. Effects of radiation parameter on temperature profile of the Cu-Kerosene Casson-Carreau nanofluid
Figure 4. Effects of Casson parameter on the velocity profile of Ag-Kerosene Casson-Carreau nanofluid
Figure 5. Effects of Casson parameter on temperature profile of Cu-Kerosene Casson-Carreau nanofluid
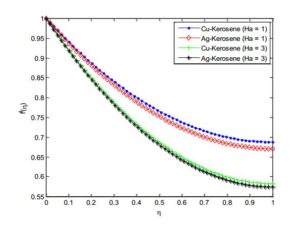
Figure 6. Effect of Magnetic field parameter (Hartmann number) on the fluid velocity distribution
Figure 7. Effect of Magnetic field parameter (Hartmann number) on the fluid temperature distribution
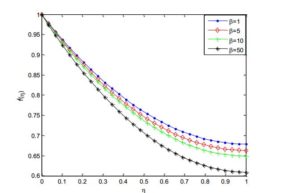
Figure 8. Effect of unsteadiness parameter on the fluid velocity distribution
Figure 9. Effect of unsteadiness parameter on the fluid temperature distribution
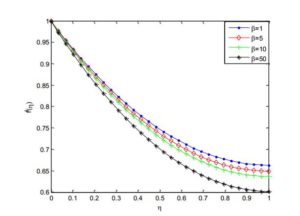
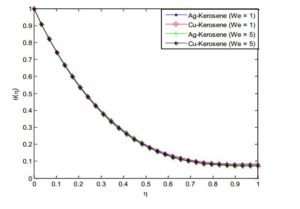
Figure 10. Effect of Weissenberg number on the fluid velocity distribution
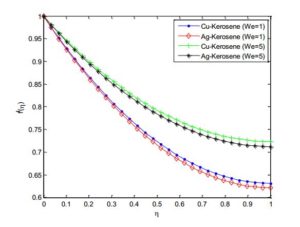
Figure 11. Effect of Weissenberg number on the fluid temperature distribution
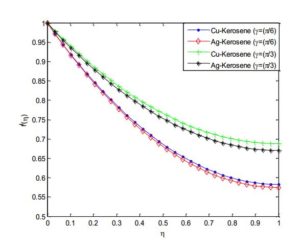
Figure 12. Effect of aligned angle on the fluid velocity distribution
Figure 13. Effect of aligned angle on the fluid temperature distribution
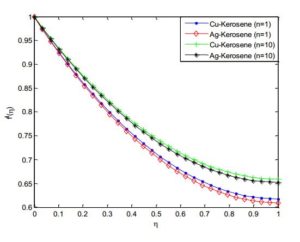
Figure 14. Effect of power-law index on the fluid velocity distribution
Figure 15. Effect of power-law index on the fluid temperature distribution
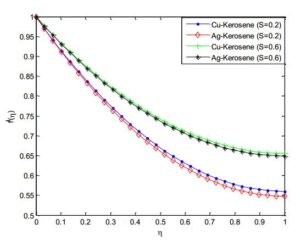
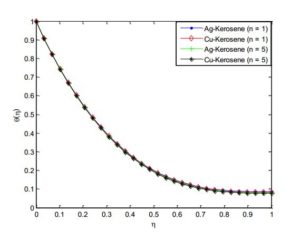
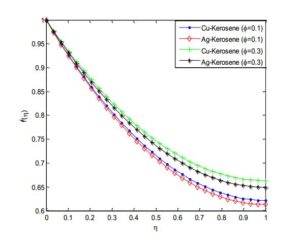
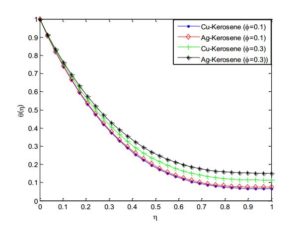
Figure 16. Effect of nanoparticle volume fractions on the fluid velocity distribution
Figure 17. Effect of nanoparticle volume fractions on the fluid temperature distribution
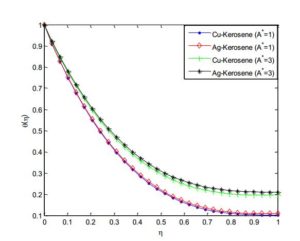
Figure 18. Effect of non-uniform heat source/sink parameter (A*) on the fluid temperature distribution
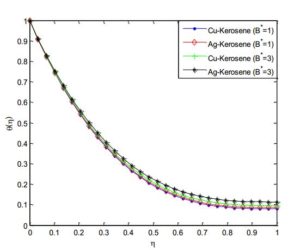
Figure 19. Effect of non-uniform heat source/sink parameter (B*) on the fluid temperature distribution
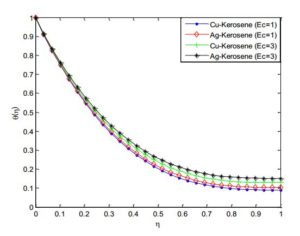
Figure 20. Effect of Eckert number on the fluid temperature distribution
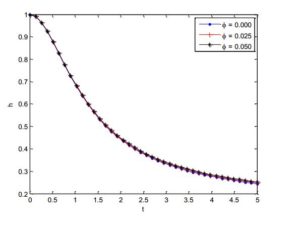
Figure 21. Variation of film thickness h with time t for different values of \(\mathrm{\phi}\)
Figures 14 and 15 demonstrated the effect of power law index on velocity and temperature fields. As the power index is increased, it was observed that the velocity profile increases while the temperature profile decreases. This is because, increasing value of the power law index, thickens the liquid film associated with an increase of the thermal boundary layer. An increase in the momentum boundary layer thickness and a decrease in thermal boundary layer thickness is observed for the increasing values of the power law index including~shear thinning~to~shear thickening~fluids. Also, it should be pointed out that an increase in Weissenberg number correspond a decrease in the local skin~friction~coefficient and the magnitude of the local Nusselt number s decreases when the Weissenberg number increases. The effects of nanoparticles volume fraction on the velocity and temperature profiles are depicted in Figures 16 and 17, respectively. The result shows that as the solid volume fraction of the film increases both the velocity and temperature field increases. This is because as the nanoparticle volume increases, more collision occurs between nanoparticles and particles with the boundary surface of the plate and consequently the resulting friction enhances the thermal conductivity of the flow and gives rise to increase the temperature within the fluid near the boundary region.
Figures 18 and 19 depict the influence of non-uniform heat source/sink parameter on the temperature field. It is revealed that increasing the non-uniform heat source/sink parameter enhances the temperature fields. It is observed in the analysis that the temperature and thermal boundary layer thickness is depressed by increasing the Prandtl number Pr. The effect of Eckert number on temperature profile is shown in Figure 20. It was established that as the values of Eckert number increases, the values of the temperature distributions in the fluid increases. This is because as Ec increases, heat energy is saved in the liquid due to the frictional heating.
The effect of nanoparticle volume fraction \(\mathrm{\phi}\) on the film thickness of the nanofluid is shown in Figure 21. It is evident from the figure that the film thickness is enhanced as the values of \(\mathrm{\phi}\) is increased. It can be inferred from Equation (15) that if nanoparticle volume fraction \(\mathrm{\phi}\) is increased, the nanofluid viscosity will increased as there exist a direct relationship or proportion between the two parameters. As a result, the increasing viscosity resists the fluid motion along the stretching direction leading to the slowdown of the film thinning process [54].
5. Conclusion
In this paper, combined influences of thermal radiation, inclined magnetic field and temperature-dependent internal heat generation on unsteady two-dimensional flow and heat transfer analysis of dissipative Casson-Carreau nanofluid over a stretching sheet embedded in a porous medium have been investigated examined numerically with the aid of finite difference method. Using kerosene as the base fluid embedded with the silver (Ag) and copper (Cu) nanoparticles, the effects of other pertinent parameters on flow and heat transfer characteristics of the nanofluids are investigated and discussed. From the results, it was established temperature field and the thermal boundary layers of Ag-kerosene nanofluid are highly effective when compared with the Cu-kerosene nanofluid. Thermal and momentum boundary layers of Cu-kerosene and Ag-kerosene nanofluids are not uniform. Heat transfer rate is enhanced by increasing in power-law index and unsteadiness parameter. Skin friction coefficient and local Nusselt number can be reduced by magnetic field parameter and they can be enhanced by increasing in aligned angle. Friction factor is depreciated and the rate of heat transfer increases by increasing the Weissenberg number. This analysis can help in expanding the understanding of the thermo-fluidic behaviour of the Carreau nanofluid over a stretching sheet. Also, the present study has numerous applications involving heat transfer and other applications such as chemical sensors, biological applications, glass, solar energy transformation, electronics, petrochemical products, light-weight, heat-insulating and refractory fiberboard and metallic ceramics etc.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest:
The authors declare no conflict of interest.References
- Hayat, T., Ullah, I., Ahmad, B., & Alsaedi, A. (2017). Radiative flow of Carreau liquid in presence of Newtonian heating and chemical reaction. Results in Physics, 7, 715-722. [Google Scholor]
- Andersson, H. I., Aarseth, J. B., Braud, N., & Dandapat, B. S. (1996). Flow of a power-law fluid film on an unsteady stretching surface. Journal of Non-Newtonian Fluid Mechanics, 62(1), 1-8. [Google Scholor]
- Andersson, H. I., Bech, K. H., & Dandapat, B. S. (1992). Magnetohydrodynamic flow of a power-law fluid over a stretching sheet. International Journal of Non-Linear Mechanics, 27(6), 929-936. [Google Scholor]
- Chen, C. H. (2003). Heat transfer in a power-law fluid film over a unsteady stretching sheet. Heat and Mass Transfer, 39(8-9), 791-796.[Google Scholor]
- Dandapat, B. S., Santra, B., & Andersson, H. I. (2003). Thermocapillarity in a liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 46(16), 3009-3015.[Google Scholor]
- Dandapat, B. S., Santra, B., & Vajravelu, K. (2007). The effects of variable fluid properties and thermocapillarity on the flow of a thin film on an unsteady stretching sheet. International Journal of Heat and Mass Transfer, 50(5-6), 991-996.[Google Scholor]
- Wang, C. (2006). Analytic solutions for a liquid film on an unsteady stretching surface. Heat and Mass Transfer, 42(8), 759-766. [Google Scholor]
- Chen, C. H. (2006). Effect of viscous dissipation on heat transfer in a non-Newtonian liquid film over an unsteady stretching sheet. Journal of Non-Newtonian Fluid Mechanics, 135(2-3), 128-135. [Google Scholor]
- Sajid, M., Hayat, T., & Asghar, S. (2007). Comparison between the HAM and HPM solutions of thin film flows of non-Newtonian fluids on a moving belt. Nonlinear Dynamics, 50(1-2), 27-35. [Google Scholor]
- Dandapat, B. S., Maity, S., & Kitamura, A. (2008). Liquid film flow due to an unsteady stretching sheet. International Journal of Non-Linear Mechanics, 43(9), 880-886.[Google Scholor]
- Abbasbandy, S., Yürüsoy, M., & Pakdemirli, M. (2008). The analysis approach of boundary layer equations of power-law fluids of second grade. Zeitschrift für Naturforschung A, 63(9), 564-570. [Google Scholor]
- Santra, B., & Dandapat, B. S. (2009). Unsteady thin-film flow over a heated stretching sheet. International Journal of Heat and Mass Transfer, 52(7-8), 1965-1970.[Google Scholor]
- Sajid, M., Ali, N., & Hayat, T. (2009). On exact solutions for thin film flows of a micropolar fluid. Communications in nonlinear science and numerical simulation, 14(2), 451-461. [Google Scholor]
- Noor, N. F. M., & Hashim, I. (2010). Thermocapillarity and magnetic field effects in a thin liquid film on an unsteady stretching surface. International Journal of Heat and Mass Transfer, 53(9-10), 2044-2051. [Google Scholor]
- Dandapat, B. S., & Chakraborty, S. (2010). Effects of variable fluid properties on unsteady thin-film flow over a non-linear stretching sheet. International Journal of Heat and Mass Transfer, 53(25-26), 5757-5763.[Google Scholor]
- Dandapat, B. S., & Singh, S. K. (2011). Thin film flow over a heated nonlinear stretching sheet in presence of uniform transverse magnetic field. International Communications in Heat and Mass Transfer, 38(3), 324-328.[Google Scholor]
- Abdel-Rahman, G. M. (2011). Effect of magnetohydrodynamic on thin films of unsteady micropolar fluid through a porous medium. Journal of Modern Physics, 2(11), 1290-1304. [Google Scholor]
- Khan, Y., Wu, Q., Faraz, N., & Yildirim, A. (2011). The effects of variable viscosity and thermal conductivity on a thin film flow over a shrinking/stretching sheet. Computers & Mathematics with Applications, 61(11), 3391-3399. [Google Scholor]
- Liu, I. C., Megahed, A. M., & Wang, H. H. (2013). Heat transfer in a liquid film due to an unsteady stretching surface with variable heat flux. Journal of Applied Mechanics, 80(4), 1-7. [Google Scholor]
- Vajravelu, K., Prasad, K. V., & Ng, C. O. (2012). Unsteady flow and heat transfer in a thin film of Ostwald–de Waele liquid over a stretching surface. Communications in Nonlinear Science and Numerical Simulation, 17(11), 4163-4173. [Google Scholor]
- Liu, I., & Megahed, A. M. (2012). Homotopy perturbation method for thin film flow and heat transfer over an unsteady stretching sheet with internal heating and variable heat flux. Journal of Applied Mathematics, 2012 418527.[Google Scholor]
- Aziz, R. C., Hashim, I., & Abbasbandy, S. (2012). Effects of thermocapillarity and thermal radiation on flow and heat transfer in a thin liquid film on an unsteady stretching sheet. Mathematical Problems in Engineering, 2012 127320. [Google Scholor]
- Khader, M. M., & Megahed, A. M. (2013). Numerical simulation using the finite difference method for the flow and heat transfer in a thin liquid film over an unsteady stretching sheet in a saturated porous medium in the presence of thermal radiation. Journal of King Saud University-Engineering Sciences, 25(1), 29-34. [Google Scholor]
- Vajravelu, K., & Hadjinicolaou, A. (1997). Convective heat transfer in an electrically conducting fluid at a stretching surface with uniform free stream. International Journal of Engineering Science, 35(12-13), 1237-1244.[Google Scholor]
- Pop, I., & Na, T. Y. (1998). A note on MHD flow over a stretching permeable surface. Mechanics Research Communications, 25(3), 263-269. [Google Scholor]
- Xu, H., Liao, S. J., & Pop, I. (2007). Series solutions of unsteady three-dimensional MHD flow and heat transfer in the boundary layer over an impulsively stretching plate. European Journal of Mechanics-B/Fluids, 26(1), 15-27.[Google Scholor]
- Ishak, A., Nazar, R., & Pop, I. (2008). Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat and Mass Transfer, 44(8), 921. [Google Scholor]
- Ishak, A., Jafar, K., Nazar, R., & Pop, I. (2009). MHD stagnation point flow towards a stretching sheet. Physica A: Statistical Mechanics and its Applications, 388(17), 3377-3383.[Google Scholor]
- AboEldahab, E. M. (2000). Radiation effect on heat transfer in an electrically conducting fluid at a stretching surface with a uniform free stream. Journal of Physics D: Applied Physics, 33(24), 3180.[Google Scholor]
- Reddy, M. G. (2014). Influence of magnetohydrodynamic and thermal radiation boundary layer flow of a nanofluid past a stretching sheet. Journal of Scientific Research, 6(2), 257-272. [Google Scholor]
- Abo-Eldahab, E. M., & El Gendy, M. S. (2000). Radiation effect on convective heat transfer in an electrically conducting fluid at a stretching surface with variable viscosity and uniform free stream. Physica Scripta, 62(4), 321. [Google Scholor]
- Reddy, M. G. (2014). Thermal radiation and chemical reaction effects on MHD mixed convective boundary layer slip flow in a porous medium with heat source and Ohmic heating. The European Physical Journal Plus, 129(3), 41.[Google Scholor]
- Reddy, M. G. (2014). Effects of Thermophoresis, Viscous Dissipation and Joule Heating on Steady MHD Flow over an Inclined Radiative Isothermal Permeable Surface with Variable Thermal Conductivity. Journal of Applied Fluid Mechanics, 7(1), 51-61. [Google Scholor]
- Raptis A, Perdikis C. Viscoelastic flow by the presence of radiation. Zeitschrift f\"{u}r Angewandte Mathematik und Mechanik (ZAMM) 1998; 78:277--9 [Google Scholor]
- Seddeek, M. A. (2002). Effects of radiation and variable viscosity on a MHD free convection flow past a semi-infinite flat plate with an aligned magnetic field in the case of unsteady flow. International Journal of Heat and Mass Transfer, 45(4), 931-935. [Google Scholor]
- Mabood, F., Imtiaz, M., Alsaedi, A., & Hayat, T. (2016). Unsteady convective boundary layer flow of Maxwell fluid with nonlinear thermal radiation: a numerical study. International Journal of Nonlinear Sciences and Numerical Simulation, 17(5), 221-229. [Google Scholor]
- Hayat, T., Muhammad, T., Alsaedi, A., & Alhuthali, M. S. (2015). Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. Journal of Magnetism and Magnetic Materials, 385, 222-229. [Google Scholor]
- Farooq, M., Khan, M. I., Waqas, M., Hayat, T., Alsaedi, A., & Khan, M. I. (2016). MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects. Journal of molecular liquids, 221, 1097-1103. [Google Scholor]
- Shehzad, S. A., Abdullah, Z., Alsaedi, A., Abbasi, F. M., & Hayat, T. (2016). Thermally radiative three-dimensional flow of Jeffrey nanofluid with internal heat generation and magnetic field. Journal of Magnetism and Magnetic Materials, 397, 108-114. [Google Scholor]
- Lin, Y., Zheng, L., Zhang, X., Ma, L., & Chen, G. (2015). MHD pseudo-plastic nanofluid unsteady flow and heat transfer in a finite thin film over stretching surface with internal heat generation. International Journal of Heat and Mass Transfer, 84, 903-911. [Google Scholor]
- Sandeep, N., Sulochana, C., & Animasaun, I. L. (2016). Stagnation-point flow of a Jeffrey nanofluid over a stretching surface with induced magnetic field and chemical reaction. In International Journal of Engineering Research in Africa (Vol. 20, pp. 93-111). Trans Tech Publications. [Google Scholor]
- Tawade, L., Abel, M., Metri, P. G., & Koti, A. (2016). Thin film flow and heat transfer over an unsteady stretching sheet with thermal radiation, internal heating in presence of external magnetic field. Int. J. Adv. Appl. Math. Mech, 3(29), 29-40.[Google Scholor]
- Raju, C. S. K., & Sandeep, N. (2016). Unsteady three-dimensional flow of Casson–Carreau fluids past a stretching surface. Alexandria Engineering Journal, 55(2), 1115-1126. [Google Scholor]
- Raju, C. S. K., & Sandeep, N. (2016). Falkner-Skan flow of a magnetic-Carreau fluid past a wedge in the presence of cross diffusion effects. The European Physical Journal Plus, 131(8), 267.[Google Scholor]
- Raju, C. S. K., Sandeep, N., Babu, M. J., & Sugunamma, V. (2016). Dual solutions for three-dimensional MHD flow of a nanofluid over a nonlinearly permeable stretching sheet. Alexandria Engineering Journal, 55(1), 151-162. [Google Scholor]
- Sandeep, N., Koriko, O. K., & Animasaun, I. L. (2016). Modified kinematic viscosity model for 3D-Casson fluid flow within boundary layer formed on a surface at absolute zero. Journal of Molecular Liquids, 221, 1197-1206. [Google Scholor]
- Babu, M. J., Sandeep, N., & Raju, C. S. (2016). Heat and mass transfer in MHD Eyring-Powell nanofluid flow due to cone in porous medium. International Journal of Engineering Research in Africa, 19, 57-74. [Google Scholor]
- Animasaun, I. L., Raju, C. S. K., & Sandeep, N. (2016). Unequal diffusivities case of homogeneous–heterogeneous reactions within viscoelastic fluid flow in the presence of induced magnetic-field and nonlinear thermal radiation. Alexandria Engineering Journal, 55(2), 1595-1606.[Google Scholor]
- Makinde, O. D., & Animasaun, I. L. (2016). Thermophoresis and Brownian motion effects on MHD bioconvection of nanofluid with nonlinear thermal radiation and quartic chemical reaction past an upper horizontal surface of a paraboloid of revolution. Journal of Molecular liquids, 221, 733-743. [Google Scholor]
- Makinde, O. D., & Animasaun, I. L. (2016). Bioconvection in MHD nanofluid flow with nonlinear thermal radiation and quartic autocatalysis chemical reaction past an upper surface of a paraboloid of revolution. International Journal of Thermal Sciences, 109, 159-171.[Google Scholor]
- Sandeep, N. (2017). Effect of aligned magnetic field on liquid thin film flow of magnetic-nanofluids embedded with graphene nanoparticles. Advanced Powder Technology, 28(3), 865-875. [Google Scholor]
- Reddy, J. R., Sugunamma, V., & Sandeep, N. (2017). Effect of frictional heating on radiative ferrofluid flow over a slendering stretching sheet with aligned magnetic field. The European physical journal plus, 132(1), 7. [Google Scholor]
- Ali, M. E., & Sandeep, N. (2017). Cattaneo-Christov model for radiative heat transfer of magnetohydrodynamic Casson-ferrofluid: a numerical study. Results in physics, 7, 21-30. [Google Scholor]
- Maity, S., Ghatani, Y., & Dandapat, B. S. (2016). Thermocapillary flow of a thin nanoliquid film over an unsteady stretching sheet. Journal of Heat Transfer, 138(4), 042401. [Google Scholor]
- Carreau, P. J. (1972). Rheological equations from molecular network theories. Transactions of the Society of Rheology, 16(1), 99-127. [Google Scholor]
- Kumar, M. S., Sandeep, N., & Kumar, B. R. (2017). Free convective heat transfer of mhd dissipative Carreau nanofluid flow over a stretching sheet. Journal of Frontier in Heat and Mass Transfer, 8, 003013. [Google Scholor]
- Hayat, T., Saleem, N., Asghar, S., Alhothuali, M. S., & Alhomaidan, A. (2011). Influence of induced magnetic field and heat transfer on peristaltic transport of a Carreau fluid. Communications in Nonlinear Science and Numerical Simulation, 16(9), 3559-3577.[Google Scholor]
- Olajuwon, B. I. (2011). Convection heat and mass transfer in a hydromagnetic Carreau fluid past a vertical porous plate in presence of thermal radiation and thermal diffusion. Thermal Science, 15(2), S241-S252. [Google Scholor]
- Hayat, T., Asad, S., Mustafa, M., & Alsaedi, A. (2014). Boundary layer flow of Carreau fluid over a convectively heated stretching sheet. Applied Mathematics and Computation, 246, 12-22. [Google Scholor]
- Akbar, N. S., Nadeem, S., Haq, R. U., & Ye, S. (2014). MHD stagnation point flow of Carreau fluid toward a permeable shrinking sheet: dual solutions. Ain Shams Engineering Journal, 5(4), 1233-1239. [Google Scholor]
- Akbar, N. S. (2014). Blood flow of Carreau fluid in a tapered artery with mixed convection. International Journal of Biomathematics, 7(06), 1450068. [Google Scholor]
- MEKHEIMER, K. S., SALAMA, F., & ELKOT, M. (2014). The unsteady flow of a Carreau fluid through inclined catheterized arteries having a balloon with time-variant overlapping stenosis. Walailak Journal of Science and Technology (WJST), 12(10), 863-883. [Google Scholor]
- Elmaboud, Y. A., Mekheimer, K. S., & Mohamed, M. S. (2015). Series solution of a natural convection flow for a Carreau fluid in a vertical channel with peristalsis. Journal of Hydrodynamics, Ser. B, 27(6), 969-979. [Google Scholor]
- Khan, M. (2016). A revised model to analyze the heat and mass transfer mechanisms in the flow of Carreau nanofluids. International Journal of Heat and Mass Transfer, 103, 291-297. [Google Scholor]
- Machireddy, G. R., & Naramgari, S. (2016). Heat and mass transfer in radiative MHD Carreau fluid with cross diffusion. Ain Shams Engineering Journal, 9(4), 1189-1204. [Google Scholor]
- Sulochana, C., Ashwinkumar, G. P., & Sandeep, N. (2016). Transpiration effect on stagnation-point flow of a Carreau nanofluid in the presence of thermophoresis and Brownian motion. Alexandria Engineering Journal, 55(2), 1151-1157. [Google Scholor]
- N. Casson, Rheology of Dispersed System, vol.84, Pergamon Press, Oxford, UK, 1959. [Google Scholor]
- Casson, N. (1959). A flow equation for pigment-oil suspensions of the printing ink type. Rheology of disperse systems.[Google Scholor]
- Dash, R. K., Mehta, K. N., & Jayaraman, G. (1996). Casson fluid flow in a pipe filled with a homogeneous porous medium. International Journal of Engineering Science, 34(10), 1145-1156. [Google Scholor]
- Andersson, H. I., Aarseth, J. B., Braud, N., & Dandapat, B. S. (1996). Flow of a power-law fluid film on an unsteady stretching surface. Journal of Non-Newtonian Fluid Mechanics, 62(1), 1-8.[Google Scholor]
- Sajid, M., Ahmad, I., Hayat, T., & Ayub, M. (2009). Unsteady flow and heat transfer of a second grade fluid over a stretching sheet. Communications in Nonlinear Science and Numerical Simulation, 14(1), 96-108. [Google Scholor]
- Eldabe, N. T. M., Saddeck, G., & El-Sayed, A. F. (2001). Heat transfer of MHD non-Newtonian Casson fluid flow between two rotating cylinders. Mechanics and Mechanical Engineering, 5(2), 237-251.[Google Scholor]
- Nadeem, S., Haq, R. U., Akbar, N. S., & Khan, Z. H. (2013). MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alexandria Engineering Journal, 52(4), 577-582.[Google Scholor]