Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2019.0022
HBA analysis of generalized viscoelastic fluids
Emran Khoshrouye Ghiasi\(^1\), Reza Saleh
Department of Mechanical Engineering, College of Engineering, Mashhad Branch, Islamic Azad University, Mashhad, Iran.; (E.K.G & R.S)
Abstract
Keywords:
1. Introduction
The practical application of viscoelastic fluids is to polymer industry, food processing, biological structure, chemical engineering etc. In general, a viscoelastic fluid can influence the transport properties of mass and momentum by varying the stability of laminar motion associated with diffusing particles [1,2]. One major difficulty dealt with such fluids is fourth-order derivative included in the Navier-Stokes momentum equation which cannot be treated using perturbation solutions. Therefore, in any given geometry, it is required to distinguish between the inflow and outflow boundaries for deformation of a fluid [3]. It is worth noting that there exist only a few works in the literature for detailed flow investigation of viscoelastic fluids within a given volume due to external fields. In this way, Rajagopal et al. [4] formulated the idea of introducing a viscoelastic fluid past a stretching wall based on Beard and Walter's theorem [5].
They could give rigorous proof of their Runge-Kutta method (RKM) by estimating the norm of series expansion and assuming, for simplicity, that the viscoelastic parameter is small but nonzero. Under this assumption, Nandeppanavar et al. [6] developed those of Subhas and Veena [17] to study phenomena like heat transfer through a porous medium with cooling processes. Furthermore, in a similar manner, Seth et al. [8], Nadeem et al. [9], Abdullah et al. [10], Chang et al. [11], Sivaraj and Kumar [12], Tariq et al. [13] and Prakash et al. [14] presented some thermodynamic review of viscoelastic fluids with both laminar flow velocity and temperature distributions.
Unlike the numerous examples of HBA, especially for cases subjected to external fields [15, 16, 17, 18, 19, 20, 21, 22, 23, 24], yet there is a lack of convergence in the choice of auxiliary parameter for analyzing the viscoelastic fluid past a stretching wall. This paper is intended only as a brief communication to represent conclusively that the HBA is useful tool for achieving much faster convergence. The rest of the paper is organized as follows.
In Section 2, a summary of governing equations based on the viscoelastic Walter's B fluid theory is reviewed. Section 3 provides the HBA and its further correspondence. Section 4 is exclusively devoted to results and discussion. The concluding remarks are summarized in Section 5.
2. Problem formulation
According to basic hypothesis of the viscoelastic Walter's B fluid theory, the governing PDEs and associated boundary conditions can be expressed as [4]3. Solution methodology
Let us suppose that the general nonlinear problem takes the form4. Results and discussion
To illustrate the computational efficiency and validity of the present HBA outlined in Section 3, the variation of shear stress at the wall versus given values of the viscoelastic parameter is compared with the semi-analytical findings analyzed by Rajagopal et al. [4]. It is to be noted here that, due to Hayat et al. [26], the auxiliary parameter in this case is selected as \(\hslash=-0.125\). Based on the results presented in Table 1, as the viscoelastic parameter is increased, the shear stress at the wall enhances and thereby reduces its flow resistance. Furthermore, it is seen that the 9th-order HBA agrees remarkably well with those reported by Rajagopal et al. [4]; because it only suffers from an error of at most 0.096% for all cases listed in Table 1. Therefore, it can be concluded that more accurate results are provided by the 9th-order HBA than those of 5th- and 7th-order ones.Table 1. Verification of the shear stress at the wall.
| H | Present (\(\hslash\)=-0.125) | Rajagopal et al. [4] | ||
|---|---|---|---|---|
| \(k\)=5 | \(k\)=7 | \(k\)=9 | ||
| 0.005 | -0.9915 | -0.9936 | -0.9965 | -0.9975 |
| 0.01 | -0.9886 | 0.9919 | -0.9939 | -0.9949 |
| 0.03 | -0.9795 | -0.9815 | -0.9837 | -0.9846 |
| 0.05 | -0.9699 | -0.9712 | -0.9729 | -0.9738 |
Figure 1. Selection of auxiliary parameter for the case \(k=9\) with the property \(Η=0.2\).
As it is seen form Figure 1, the averaged square residual error takes its minimum possible value when the auxiliary parameter is taken to be -0.122. Hence, this important finding can be considered as a tool to accelerate convergence of the present HBA.
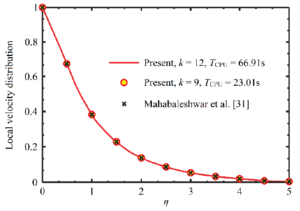
Table 2 investigates uniqueness of the present HBA theoretically by making a correspondence between the averaged square residual error and order of approximation. According to this Table 2, it is seen that increasing the order of approximation reduces monotonically the value of averaged square residual error when it is subject to the viscoelastic parameter \(Η=0.2\). Furthermore, one can say that accounting for the minimization of averaged square residual error is so essential to reduce the CPU time without any loss of accuracy. This fact is clearly shown in Figure 2.
Figure 2. Influence of the auxiliary parameter on the local velocity distribution with the property \(Η=0.2\)
Table 2. onvergence of the series expansion.
| \(\eta\) | \(k\) = 5 | \(k\) = 7 | \(k\) = 9 | |||
|---|---|---|---|---|---|---|
| \(\hslash\) | \(\triangle_{k}\) | \(\hslash\) | \(\triangle_{k}\) | \(\hslash\) | \(\triangle_{k}\) | |
| \(0\) | \(-0.115\) | \(9.89 \times 10^{10}\) | \(-0.119\) | \(7.40 \times 10^{-10}\) | \(-0.122\) | \(4.96 \times 10^{-11}\) |
| \(0.2\) | \(-0.115\) | \(1.16 \times 10^{9}\) | \(-0.119\) | \(7.69\times 10^{-10}\) | \(-0.122\) | \(5.54\times 10^{-11}\) |
| \(0.4\) | \( -0.115 \) | \(2.44\times 10^{9}\) | \( -0.119 \) | \(7.91\times 10^{-10}\) | \( -0.122 \) | \(6.23\times 10^{-11}\) |
| \(0.6\) | \( -0.115 \) | \(3.50\times 10^{9}\) | \( -0.119 \) | \(8.16\times 10^{-10} \) | \( -0.122 \) | \(6.98\times 10^{-11}\) |
| \(0.8\) | \(-0.115 \) | \(4.73\times 10^{9}\) | \(-0.119 \) | \(8.38\times 10^{-10} \) | \( -0.122 \) | \(7.75\times 10^{-11}\) |
| \(1\) | \( -0.115 \) | \(6.02\times 10^{9} \) | \( -0.119 \) | \(8.64\times 10^{-10} \) | \( -0.122 \) | \(8.39\times 10^{-11}\) |
In view of such configuration seen in Figure 2, there exists an excellent consistency between the 9th- and 12th-order HBA; that is, the local velocity distribution converges certainly for \( \hslash=-0.122\). Furthermore, it is to be noted here that this observation is in agreement with the analytical results reported by Mahabaleshwar et al. [31] for analyzing viscoelastic Walter's B fluid past a stretching wall through a porous medium.
5. Concluding remarks
This paper focused on the problem involving the momentum of viscoelastic Walter's B fluid past a stretching wall using HBA. The QRL was employed to introduce a criterion for minimizing the averaged square residual error at each step. The present findings are compared and verified by those available results in the open literature. Here, the main conclusions are summarized as- The 9th-order HBA represents a high accuracy approximation than 5th- and 7th-order ones.
- Using the auxiliary parameter \(\hslash=-0.122\) yields an absolutely convergent series expansion.
- The CPU time will be decreased when the averaged square residual error is minimized.
- Because of the difficulty in evaluating the fourth-order derivative of Equation (3), the 9th-order HBA is applicable only when the initial guess is proportional to the boundary conditions given in Equation (4).
Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest:
The authors declare no conflict of interest.References
- Saramito, P. (2016). Complex fluids: Modelling and algorithms. Switzerland: Springer.[Google Scholor]
- Page, J., & Zaki, T. A. (2014). Streak evolution in viscoelastic Couette flow. Journal of Fluid Mechanics, 742, 520-551. [Google Scholor]
- Siginer, D. A. (2014). Stability of non-linear constitutive formulations for viscoelastic fluids. Springer International Publishing. [Google Scholor]
- Rajagopal, K. R., Na, T. Y., & Gupta, A. S. (1984). Flow of a viscoelastic fluid over a stretching sheet. Rheologica Acta, 23(2), 213-215. [Google Scholor]
- Beard, D. W., & Walters, K. (1964, July). Elastico-viscous boundary-layer flows I. Two-dimensional flow near a stagnation point. In Mathematical Proceedings of the Cambridge Philosophical Society (Vol. 60, No. 3, pp. 667-674). Cambridge University Press. [Google Scholor]
- Nandeppanavar, M. M., Abel, M. S., & Tawade, J. (2010). Heat transfer in a Walter's liquid B fluid over an impermeable stretching sheet with non-uniform heat source/sink and elastic deformation. Communications in Nonlinear Science and Numerical Simulation, 15(7), 1791-1802. [Google Scholor]
- Subhas, A., & Veena, P. (1998). Visco-elastic fluid flow and heat transfer in a porous medium over a stretching sheet. International Journal of Non-Linear Mechanics, 33(3), 531-540. [Google Scholor]
- Seth, G. S., Mishra, M. K., & Tripathi, R. (2018). MHD free convective heat transfer in a Walter's liquid-B fluid past a convectively heated stretching sheet with partial wall slip. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 40(2), 103. [Google Scholor]
- Nadeem, S., Mehmood, R., & Motsa, S. S. (2015). Numerical investigation on MHD oblique flow of Walter's B type nano fluid over a convective surface. International Journal of Thermal Sciences, 92, 162-172. [Google Scholor]
- Abdullah, M., Butt, A. R., & Raza, N. (2019). Heat transfer analysis of Walters'-B fluid with Newtonian heating through an oscillating vertical plate by using fractional Caputo-Fabrizio derivatives. Mechanics of Time-Dependent Materials, 23(2), 133-151. [Google Scholor]
- Chang, T. B., Mehmood, A., Beg, O. A., Narahari, M., Islam, M. N., & Ameen, F. (2011). Numerical study of transient free convective mass transfer in a Walters-B viscoelastic flow with wall suction. Communications in Nonlinear Science and Numerical Simulation, 16(1), 216-225. [Google Scholor]
- Sivaraj, R., & Kumar, B. R. (2013). Viscoelastic fluid flow over a moving vertical cone and flat plate with variable electric conductivity. International Journal of Heat and Mass Transfer, 61, 119-128. [Google Scholor]
- Ramesh, K., & Devakar, M. (2018). Influence of magnetohydrodynamics on peristaltic flow of a Walters B fluid in an inclined asymmetric channel with heat transfer. World Journal of Engineering, 15(4), 450-467. [Google Scholor]
- Prakash, O., Kumar, D., & Dwivedi, Y. K. (2012). Heat transfer in MHD flow of dusty viscoelastic (Walters' liquid model-B) stratified fluid in porous medium under variable viscosity. Pramana, 79(6), 1457-1470. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2018). Unsteady shrinking embedded horizontal sheet subjected to inclined Lorentz force and Joule heating, an analytical solution. Results in Physics, 11, 65-71. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2019). Homotopy analysis method for the Sakiadis flow of a thixotropic fluid. The European Physical Journal Plus, 134(1), 32. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2019). A convergence criterion for tangent hyperbolic fluid along a stretching wall subjected to inclined electromagnetic field. SeMA Journal, 76(3), 521-531. [Google Scholor]
- E. Khoshrouye Ghiasi, R. Saleh, Non-dimensional optimization of magnetohydrodynamic Falkner-Skan fluid flow, INAE Lett. 3(3) (2018) 143-147. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2019). Nonlinear stability and thermomechanical analysis of hydromagnetic Falkner–Skan Casson conjugate fluid flow over an angular-geometric surface based on Buongiorno's model using homotopy analysis method and its extension. Pramana, 92(1), 12. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2019). Analytical and numerical solutions to the 2D Sakiadis flow of Casson fluid with cross diffusion, inclined magnetic force, viscous dissipation and thermal radiation based on Buongiorno's mathematical model. CFD Lett, 11(1), 40-54. [Google Scholor]
- Khoshrouye Ghiasi, E., & Saleh, R. (2018). 2D flow of Casson fluid with non-uniform heat source/sink and Joule heating. Frontiers in Heat and Mass Transfer (FHMT), 12. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2018). Optimal homotopy asymptotic method-based Galerkin approach for solving generalized Blasius boundary value problem. Journal of Advanced Physics, 7(3), 408-411. [Google Scholor]
- Ghiasi, E. K., & Saleh, R. (2019). On approximation of FBVP by homotopy-based truncation technique. SeMA Journal. https://doi.org/10.1007/s40324-019-00193-y. [Google Scholor]
- Khoshrouye Ghiasi, E. & Saleh, R. (2019). A series solution for melting heat transfer characteristics of hybrid Casson fluid under thermal radiation. Adv. Sci. Eng. Med. Author could not provide DOI for this article in press [Google Scholor]
- Liao, S. (2003). Beyond perturbation: introduction to the homotopy analysis method. Chapman and Hall/CRC. [Google Scholor]
- Hayat, T., Qayyum, S., Shehzad, S. A., & Alsaedi, A. (2017). Chemical reaction and heat generation/absorption aspects in flow of Walters-B nanofluid with Cattaneo-Christov double-diffusion. Results in physics, 7, 4145-4152.[Google Scholor]
- Yabushita, K., Yamashita, M., & Tsuboi, K. (2007). An analytic solution of projectile motion with the quadratic resistance law using the homotopy analysis method. Journal of Physics A: Mathematical and theoretical, 40(29), 8403. [Google Scholor]
- Liao, S. (2010). An optimal homotopy-analysis approach for strongly nonlinear differential equations. Communications in Nonlinear Science and Numerical Simulation, 15(8), 2003-2016. [Google Scholor]
- Liao, S. (2012). Homotopy analysis method in nonlinear differential equations (pp. 153-165). Beijing: Higher education press. [Google Scholor]
- Liao, S. (2009). Notes on the homotopy analysis method: some definitions and theorems. Communications in Nonlinear Science and Numerical Simulation, 14(4), 983-997. [Google Scholor]
- Mahabaleshwar, U. S., Sarris, I. E., & Lorenzini, G. (2018). Effect of radiation and Navier slip boundary of Walters' liquid B flow over a stretching sheet in a porous media. International Journal of Heat and Mass Transfer, 127, 1327-1337. [Google Scholor]