INFORMATION MENU
Full-Text PDF

Engineering and Applied Science Letter

Vol. 2 (2019), Issue 4, pp. 33 – 44
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2019.0029

Generalized dynamics on the penetration of two phase fuel spray using differential transform method

B. Y. Ogunmola, A. A. Yinusa\(^1\)
Mechanical Engineering Department, University of Lagos, Nigeria.; (B.Y.O & A.A.Y)

\(^{1}\)Corresponding Author: mynotebook2010@yahoo.com
Copyright ©2019 B. Y. Ogunmola, A. A. Yinusa. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: May 11, 2019 – Accepted: October 20, 2019 – Published: December 16, 2019

Abstract

The penetration of fuel spray as a result of the mixture of fuel droplet and entrained air usually generate nonlinear models whose solutions are normally difficult to realize analytically. This present study presents general approximate analytical solution to such problem by employing Differential transform Method (DTM). At the level of two-phase flow, the spray droplets and the entrained air have the same flow velocity. In order to fully understand the process, the parameters present in the governing equations are carefully studied. The obtained solution employing DTM is verified with Numerical Runge-Kutta (RKF45) and also compared with similar past works. Furthermore, the acquired results for different ambient densities and injection velocities are depicted and discussed. The results illustrate that continuous increase in the initial velocity and orifice diameter cause a corresponding increase in spray penetration while an antonymous effect is noticed for an increased semi cone angle and density. This work will find vital applications in the optimization of systems whose operation are influence by the aforementioned spray penetration processes.

Keywords:

Differential transform method, entrained air, fuel spray penetration, Runge-Kutta method, two phase flow.

1. Introduction

The science of how fuel spray penetration affect physical and engineering systems has been an interesting subject of interest. These systems whose operations are influenced by the aforementioned penetration processes include combustion chambers, gas turbines, thrust engines, agricultural spray systems, vapor diffusion and distribution processes and general gas turbulence operations. Adequate monitoring and prediction of the flow dynamics associated with fuel spray penetration thus require great attention. As a result, different studies have been flagged up from experimental, analytical and numerical point of views. This include the tremendous work by Szchin et al. , [1]. In their work, they presented a penetration model for fuel spray and performed different parametric studies by basically focusing on the impact of density, pressure and semi spray cone angle on spray penetration. They went further to perform an experiment for the validation of some of their results. They concluded by establishing mathematical relations between the fuel spray term and some vital parameters. In a different study, the penetration of liquid in diesel spray focusing on two fluid flow model has been critically considered [2, 3].

The systems were studied under steady condition with the impact of the injection droplet size cell investigated. Loth et al. , [4] applied numerical methods for motion of dispersed particles, droplets and bubbles to properly investigate the dispersion and spray penetration phenomenon while Pozorski et al. , [5] further did a study by considering turbulent spray penetration fluid flow. It has also been established that structure and break up properties of sprays are attributes that should be considered when performing analysis on the dynamics of fuel sprays [6]. Due to the aforementioned effects, Ganji et al. , [7] did an extension on the modelling work of spray penetration by studying the impact of nonlinear turbulence model on the spray performance in a two-phase flow. Ebrahimian et al. , [8] presented an approximate analytical solution by employing Variational iteration method (VIM) to examine the initial stage of fuel spray penetration. Bararnia et al. , [9] presented a solution of the Falkner-Skan wedge flow by HPM Padé method. Mebine et al. , [10] generated a unified model for fuel spray penetration, Ghosh et al. , [11] did a study on induced air velocity within droplet driven sprays and Jalilpour et al. , [12] obtained an approximate analytical solution of analytical model for fuel spray penetration using Pade - homotopy perturbation method (HPM) by considering both initial and two phase fluid. They also verified the Pade HPM with an efficient numerical scheme. In [13, 14, 15, 16], authors applied the Adomian decomposition method, DJ method and Variation of parameter method (VPM) to study the thermal and environmental behaviour of oxidizing micro-dust that is susceptible to combustion. Furthermore, Yinusa and Sobamowo [17] presented the analysis of dynamic behaviour of a tensioned Carbon nanotube in thermal and pressurized environments. They employed integral transform to solve the governing model and obtain the dynamic behaviour and stability criteria of the carbon nanotube. Hikmah et al., et al. [18] did an elementary study on the impact of tea dust geometry and size on its explosion using some food particles. Furthermore, the classical DTM, Multi-step DTM (MsDTM) as well as other approximate and total analytical schemes have been widely employed to solve different governing equations as applied to different research areas [19, 20, 21, 22, 23, 24].

Motivated by the previous works, this work introduces a generalized analytical solution for generating and monitoring two phase fuel spray dynamics using differential transform method (DTM). The method is verified, compared and validated in order to ascertain the efficiency and appropriateness of the scheme.

2. Description of problem and governing the equation

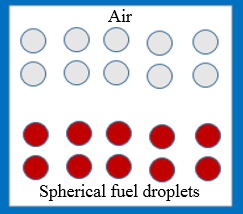
Consider the spherical shaped fuel droplets with entrained air as shown in Figure 1. These two components form air-fuel mixtures in proportions usually well specified. The study of the influence of air jet on fuel spray generates strong nonlinear model that is difficult to solve generally using an analytical scheme for a specified air jet velocity. Also, an augmentation in the nozzle distance causes the velocity of the fuel droplets to be approximately equal to the velocity of the air entrained. This equality in velocity can be used to model the dynamical process as a two phase flow involving the spray droplets and the air jet. In order to derive the flow and penetration model for the process, the continuity and Navier stoke equations are employed as shown below [12]:

Figure 1. Schematic of air and spherical fuel mixture

The continuity equation is: \begin{align*} (Continuity of air - fuel mixture) = (Continuity of entrained air) + (Continuity of fuel spray droplet) \end{align*}
\begin{align} (\rho vA)_m = (\rho v A)_a + (\rho v A)_f, \end{align}
(1)
which when simplifies becomes
\begin{align} \rho_dv_i A_0 + (1 + \alpha_d) \rho_m v_m A_g = \rho_m v_m A_m. \end{align}
(2)
The momentum equation is:
\begin{align} \rho_d v_i^2 A_0 = \rho_m v_m^2 A_m \end{align}
(3)
By incorporating the geometrical assumptions as described by Jalilpour et al. , [12], the nonlinear governing equation becomes
\begin{align} \label{equ4} \frac{d \zeta}{d \tau} = -(k_1 + k_2 \zeta + k_3 \zeta^2)^2 \frac{d \zeta}{d \tau} + 2 v_i \end{align}
(4)
where \(k_1 = 4(1 - \alpha_d) \rho + 1,\) \( k_2 = \frac{4(1 - \alpha_d) \rho \ tan \Theta}{D_0} \) and \( k_3 = \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2}. \) Then the generalized model becomes
\begin{equation}\label{equ8} \dfrac{d \zeta}{d \tau} = - \bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg)^n \dfrac{d \zeta}{d \tau} + 2 v_i \end{equation}
(5)
subject to the initial condition \( \zeta(0) = 0.\) Recall that the nonlinear governing equation as shown in Equation (4) may be expressed as
\begin{align} \label{equ10} \dfrac{d \zeta}{d \tau} + \bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg)^n \dfrac{d \zeta}{d \tau} - 2 v_i = 0 \end{align}
(6)
Since it is part of the aim of the present study to establish a generalized solution to the model, then the index \(n\) should be well taken care of. This will be obtained following the procedures below. Let \begin{align*} f = \bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \ tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg)^n \end{align*} Equation (6) becomes;
\begin{align} \label{equ12} \frac{d \zeta}{d \tau} + f \frac{d \zeta}{d \tau} - 2 v_i = 0 \end{align}
(7)
We need to generate a differential equation for the function f in Equation (7). This is achieved by employing the chain rule as shown below: \begin{align*} \frac{df}{d\tau} = \frac{df}{d \tau} \frac{d \zeta}{d \tau} \end{align*} Performing the differentiation, we get
\( \frac{df}{d \tau} = n\bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg)^{n-1} \times \bigg(\bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \\+ 2 \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta \bigg) \frac{d \zeta}{d \tau} \)
simplifying the resulting equation, we get
\( \frac{df}{d \tau} = n \frac{\bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg)^n}{\bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg)} \times \bigg(\bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) + 2 \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta \bigg) \frac{d \zeta}{d \tau} \)
The two coupled differential equations shown will then be solved simultaneously in order to obtain an analytical solution for \(\zeta(\tau)\) considering any value of the exponent \(n\).
\( \bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg) \frac{df}{d \tau} - n \times \bigg(\bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \\+ 2 \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta \bigg) f \frac{d \zeta}{d \tau} = 0 \)
\begin{align} \frac{d \zeta}{d \tau} + f \frac{d \zeta}{d \tau} - 2v_i = 0 \end{align}
(8)

3. Methods of solution

As a result of the presence of the nonlinear terms in Equation (5), obtaining an exact solution becomes uneasy. The usual practice is to employ numerical schemes. However, recently, several semi- or approximate analytical methods have been developed to handle nonlinear equations exactly. In this study, the developed nonlinear model in Equation (5) is be solved analytically using Differential transform Method (DTM)

3.1. Basic principle: differential transform method (DTM)

The basic concept and the procedure of DTM for solving differential equations are outlined in previous works [22]. However, the DTM recursive relation for transforming models into another domain in an algebraic form is presented below:
Table 1. DTM recursive relations.
1. \(Z(t)= U(t) \pm V(t), \ \ Z(k) = U(k) \pm V(k)  \)
2. \(Z(t) = \propto U(t), \ \  Z(k) = \propto U(k)    \)
3. \(Z(t) = \dfrac{dU(t)}{dt},  \ \  Z(k) = (k+ 1) U[k+ 1]   \)
4. \(Z(t) = \dfrac{d^2U(t)}{dt^2},  \ \ Z(t) = (k+ 1) (k+ 2) U[k+ 2]\)
5. \(Z(t) = \dfrac{d^m U(t)}{dt^m},  \ \ Z(k) = (k+ 1) (k+ 2) \dots (k+ m) U[k+ m],  \ \ or \ \dfrac{(k+m)!}{k!} U[k+m]\)
6. \(Z(t) = U(t) * V(t),  \ \ Z(k) = \sum_{L= 0}^{K} V[l] U[K - l]\)
7. \(Z(t) = t^m,  \ \ Z(k) =  \delta (k - m )  = \tau_{ij} =
The Table 1 above shows the recursive relations for different operators. These relations help map a given function into another domain in an algebraic form. The solution will then be obtain by inverting the obtain series solution.

4. Method of solution: differential transform method (DTM)

Recall the coupled ODE which is to be transformed using the Table 1 above;
\begin{eqnarray}\label{equ15} &&\bigg( (4 (1 - \alpha_d) \rho + 1) + \bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) \zeta + \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta^2 \bigg) \frac{df}{d \tau} - n \notag \nonumber\\&& \times \bigg(\bigg( \frac{4(1 - \alpha_d) \rho \tan \Theta}{D_0} \bigg) + 2 \bigg( \frac{4(1 - \alpha_d) \rho \tan^2 \Theta}{D_0^2} \bigg) \zeta \bigg) f \frac{d \zeta}{d \tau} = 0 \end{eqnarray}
(9)
\begin{align} \label{equ16} \frac{d \zeta}{d \tau} +f \frac{d \zeta}{d \tau} - 2 v_i = 0 \end{align}
(10)
with initial conditions \( \zeta[0] = 0\), \( F[0] = a.\) Applying the principle of DTM transformation, the recursive relations for Equation (9) and Equation (10) are:
\begin{align} (k + 1) \zeta_{l + 1} + \sum_{ l =0}^{k } ( l + 1) \zeta_{l +1} F_{k - l} - 2v_i \delta [k] = 0 \end{align}
(11)
\( k_1 (k+ 1) F_{k+ 1} + k_2 \sum_{ l = 0}^{k } (l + 1) F_{l + 1} \zeta_{k - l} + k_2 \sum_{m = 0}^{k} \bigg( \sum_{l = 0}^{m } (l + 1) F_{l + 1}\zeta_{m - l} \zeta_{k - m} \bigg) - n \bigg( k_2 \sum_{l = 0}^{k} ( l + 1) \zeta_{l+ 1} F_{k - l} \\ + 2k_3 \sum_{m = 0}^{k} \bigg( \sum_{l = 0}^{m} (l+ 1) \zeta_{l + 1} \zeta_{m- l} F_{k -m } \bigg) \bigg)= 0 \) After iterating with the highest counter, the term by term DTM solution becomes;
\( \zeta[0 ] = 0,\)
\( \zeta[1] = 2 \dfrac{v_i}{a + 1}, \)
\( \zeta[2] = v_i \frac{ \biggl[ -8n \rho \ tan (\Theta) v_i a \alpha_d + 4 D_0 a^2 \rho \alpha_d +8 n \rho \ tan (\Theta) v_i a - 4 D_0 a^2 \rho + 8 D_0 a \rho \alpha_d - D_0 a^2 - 8 D_0 a \rho + 4 D_0 \rho \alpha_d - 2 D_0 a - 4D_0 \rho - D_0 \biggl] }{(a+ 1)^3 D_0 (4 \rho \alpha_d -4 \rho - 1) }, \)
\( \zeta[3] = \frac{2}{3} \frac{v_i}{(a+ 1)^5 D_0^2 (4 \rho \alpha_d - 4 \rho - 1)^2} \biggl[ -48 D_0 \tan (\Theta) a^3 n \rho^2 v_i + 16 (\tan (\Theta))^2 a^2 n \rho v_i^2 \alpha_d + 16 D_0^2 \rho^2 \alpha_d^2 - 32 D_0^2 \rho^2 \alpha_d - 8 D_0^2 \rho \alpha_d + \\64 (\tan (\Theta))^2 a n \rho^2 v_i^2 \alpha_d - 12 D_0 \tan (\Theta) a^3 n \rho v_i + 8 D_0^2 a^4 \rho + 64 D_0^2 a^3 \rho^2 + 16 D_0^2 a^4 \rho^2 + \\16 (\tan (\Theta))^2 a n \rho v_i^2 \alpha_d - 96 D_0 \tan (\Theta) a^2 n \rho^2 v_i - 48 D_0 \tan (\Theta) a n \rho^2 v_i - 24 D_0 \tan (\Theta) a^2 n \rho v_i - \\32 (\tan (\Theta))^2 a n \rho^2 v_i^2 - 32 (\tan (\Theta))^2 a^2 n \rho^2 v_i^2 - 32 (\tan (\Theta))^2 a n^2 \rho^2 v_i^2 - 16 (\tan (\Theta))^2 a^2 n \rho v_i^2 - \\16 (\tan (\Theta))^2 a n \rho v_i^2 + 64 (\tan (\Theta))^2 a^2 n^2 \rho^2 v_i^2 - 128 D_0^2 a \rho^2 \alpha_d - 32 D_0^2 a \rho \alpha_d - 64 (\tan (\Theta))^2 a n^2 \rho^2 v_i^2 \alpha_d- \\32 D_0^2 a^3 \rho \alpha_d - 192 D_0^2 a^2 \rho^2 \alpha_d + 64 D_0^2 a \rho^2 \alpha_d^2 - 48 D_0^2 a^2 \rho \alpha_d + 16 D_0^2 a^4 \rho^2 \alpha_d^2 - 32 D_0^2 a^4 \rho^2 \alpha_d + \\64 D_0^2 a^3 \rho^2 \alpha_d^2 - 8 D_0^2 a^4 \rho \alpha_d - 128 D_0^2 a^3 \rho^2 \alpha_d + 96 D_0^2 a^2 \rho^2 \alpha_d^2 - 12 D_0 \tan (\Theta) a n \rho v_i + 96 D_0^2 a^2 \rho^2 \\32 D_0^2 a^3 \rho^2 + 32 D_0^2 a \rho + 64 D_0^2 a \rho^2 + 48 D_0^2 a^2 \rho - 32 (\tan (\Theta))^2 a n \rho^2 v_i^2 \alpha_d^2 + 64 (\tan (\Theta))^2 a^2 n \rho^2 v_i^2 \alpha_d + \\32 (\tan (\Theta))^2 a^2 n \rho^2 v_i^2 \alpha_d^2 - 32 (\tan (\Theta))^2 a n^2 \rho^2 v_i^2 \alpha_d^2 + 64 (\tan (\Theta))^2 a^2 n^2 \rho^2 v_i^2 \alpha_d^2 - 128 (\tan (\Theta))^2 a^2 n^2 \rho^2 v_i^2 \alpha_d + \\4 D_0^2 a + 8 D_0^2 \rho + D_0^2 a^4 + 4 D_0^2 a^3 + 6 D_0^2 a^2 + 16 D_0^2 \rho^2 + D_0^2 + D_0^2 + 12 D_0 \tan (\Theta) a n \rho v_i \alpha_d+ \\96 D_0 \tan (\Theta) a n \rho^2 v_i \alpha_d + 24 D_0 \tan (\Theta) a^2 n \rho v_i \alpha_d - 48 D_0 \tan (\Theta) a n \rho^2 v_i \alpha_d^2 + 192 D_0 \tan (\Theta) a^2 n \rho^2 v_i \alpha_d + \\12 D_0 \tan (\Theta) a^3 n \rho v_i \alpha_d - 96 D_0 \tan (\Theta) a^2 n \rho^2 v_i \alpha_d^2 + 96 D_0 \tan (\Theta) a^3 n \rho^2 v_i \alpha_d - 48 D_0 \tan (\Theta) a^3 n \rho^2 v_i \alpha_d^2 \biggr]. \) Applying the principle of DTM inversion to the obtained term by term solution,
\begin{align} \zeta(\tau) = \sum_{j = 0}^{N} \zeta[j]\tau^j \end{align}
(12)
\begin{align} \zeta(\tau) = \zeta[0] + \zeta[1]\tau + \zeta[2] \tau^2 + \zeta[3] \tau^3 + \dots. \end{align}
(13)
Making necessary substitutions, the desired approximate analytical solution for the spray penetration history becomes:
\( \zeta(\tau) = \Biggl[ 2 \frac{v_i \tau}{a + 1} + v_i \frac{\biggl[ -8n \rho \ \tan (\Theta) v_i a \alpha_d + 4 D_0 a^2 \rho \alpha_d +8 n \rho \ \tan (\Theta) v_i a - 4 D_0 a^2 \rho + 8 D_0 a \rho \alpha_d - D_0 a^2 - 8 D_0 a \rho + 4 D_0 \rho \alpha_d - 2 D_0 a - 4D_0 \rho - D_0 \biggl] }{(a+ 1)^3 D_0 (4 \rho \alpha_d -4 \rho - 1) }\\\tau^2 + \frac{2}{3} \frac{v_i \tau^3}{(a+ 1)^5 D_0^2 (4 \rho \alpha_d - 4 \rho - 1)^2} \bigg[-48 D_0 \tan (\Theta) a^3 n \rho^2 v_i + 16 (\tan (\Theta))^2 a^2 n \rho v_i^2 \alpha_d + 16 D_0^2 \rho^2 \alpha_d^2 - 32 D_0^2 \rho^2 \alpha_d - 8 D_0^2 \rho \alpha_d + \\64 (\tan (\Theta))^2 a n \rho^2 v_i^2 \alpha_d - 12 D_0 \tan (\Theta) a^3 n \rho v_i + 8 D_0^2 a^4 \rho + 64 D_0^2 a^3 \rho^2 + 16 D_0^2 a^4 \rho^2 + \\16 (\tan (\Theta))^2 a n \rho v_i^2 \alpha_d - 96 D_0 \tan (\Theta) a^2 n \rho^2 v_i - 48 D_0 \tan (\Theta) a n \rho^2 v_i - 24 D_0 \tan (\Theta) a^2 n \rho v_i - \\32 (\tan (\Theta))^2 a n \rho^2 v_i^2 - 32 (\tan (\Theta))^2 a^2 n \rho^2 v_i^2 - 32 (\tan (\Theta))^2 a n^2 \rho^2 v_i^2 - 16 (\tan (\Theta))^2 a^2 n \rho v_i^2 - \\16 (\tan (\Theta))^2 a n \rho v_i^2 + 64 (\tan (\Theta))^2 a^2 n^2 \rho^2 v_i^2 - 128 D_0^2 a \rho^2 \alpha_d - 32 D_0^2 a \rho \alpha_d - 64 (\tan (\Theta))^2 a n^2 \rho^2 v_i^2 \alpha_d - \\32 D_0^2 a^3 \rho \alpha_d - 192 D_0^2 a^2 \rho^2 \alpha_d + 64 D_0^2 a \rho^2 \alpha_d^2 - 48 D_0^2 a^2 \rho \alpha_d + 16 D_0^2 a^4 \rho^2 \alpha_d^2 - 32 D_0^2 a^4 \rho^2 \alpha_d + \\64 D_0^2 a^3 \rho^2 \alpha_d^2 - 8 D_0^2 a^4 \rho \alpha_d - 128 D_0^2 a^3 \rho^2 \alpha_d + 96 D_0^2 a^2 \rho^2 \alpha_d^2 - 12 D_0 \tan (\Theta) a n \rho v_i + 96 D_0^2 a^2 \rho^2 + \\32 D_0^2 a^3 \rho^2 + 32 D_0^2 a \rho + 64 D_0^2 a \rho^2 + 48 D_0^2 a^2 \rho - 32 (\tan (\Theta))^2 a n \rho^2 v_i^2 \alpha_d^2 + 64 (\tan (\Theta))^2 a^2 n \rho^2 v_i^2 \alpha_d + \\32 (\tan (\Theta))^2 a^2 n \rho^2 v_i^2 \alpha_d^2 - 32 (\tan (\Theta))^2 a n^2 \rho^2 v_i^2 \alpha_d^2 + 64 (\tan (\Theta))^2 a^2 n^2 \rho^2 v_i^2 \alpha_d^2 - \\128 (\tan (\Theta))^2 a^2 n^2 \rho^2 v_i^2 \alpha_d + 4 D_0^2 a + 8 D_0^2 \rho + D_0^2 a^4 + 4 D_0^2 a^3 + 6 D_0^2 a^2 + 16 D_0^2 \rho^2 + D_0^2 + D_0^2 + 12 D_0 \tan (\Theta) a n \rho v_i \alpha_d+ \\96 D_0 \tan (\Theta) a n \rho^2 v_i \alpha_d + 24 D_0 \tan (\Theta) a^2 n \rho v_i \alpha_d - 48 D_0 \tan (\Theta) a n \rho^2 v_i \alpha_d^2 + 192 D_0 \tan (\Theta) a^2 n \rho^2 v_i \alpha_d + \\12 D_0 \tan (\Theta) a^3 n \rho v_i \alpha_d - 96 D_0 \tan (\Theta) a^2 n \rho^2 v_i \alpha_d^2 + 96 D_0 \tan (\Theta) a^3 n \rho^2 v_i \alpha_d - 48 D_0 \tan (\Theta) a^3 n \rho^2 v_i \alpha_d^2\bigg] \Biggr]. \)

5. Results and Discussion

5.1. Verification

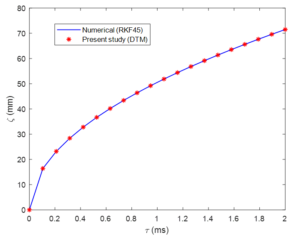
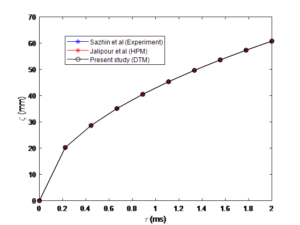
The verification of the analytical method employed in the present study is shown in Figure 2 with the numerical values displayed in Table \ref{table2}. The graph and table confirm the efficiency of the DTM used as excellent agreements are noticed.

5.2. Effect of Droplet initial velocity on spray penetration

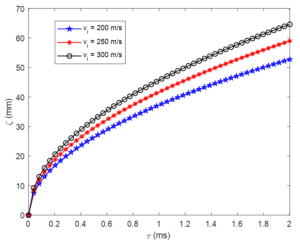
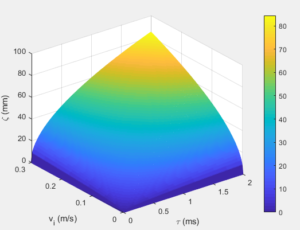
Figure 3 depicts the influence of droplet initial velocity on spray penetration for the two phase fluid flow considered. An increase in the initial velocity increases the spray penetration as a result of the increase in the diffusion capability of the air-fuel mixture. This initial spray velocity is important and can be used to monitor the penetration history of the spray when in used.

Figure 3. Effect of droplet initial velocity

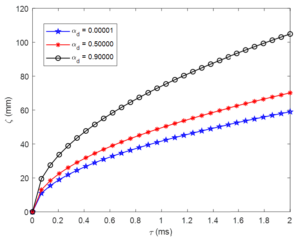
5.3. Effect of droplet volume fraction on spray penetration

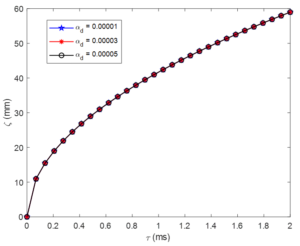
Figure 4 and Figure 5 show the influence of droplet volume fraction on spray penetration. The impact illustrates negligible effect of the volume fraction term on the spray penetration for small values and close values. However, for increased and large space values, noticeable influences begin to spring up. This constant parameter has a proportional relationship with spray penetration.

Figure 4. Effect of droplet volume fraction

Figure 5. Effect of droplet volume fraction

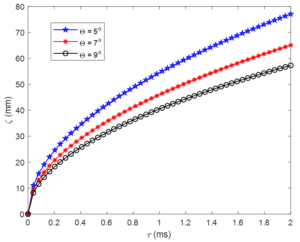
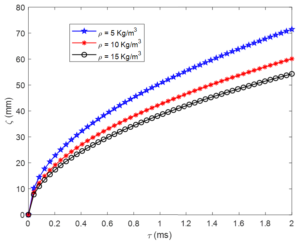
5.4. Effect of half cone angle and density on spray penetration

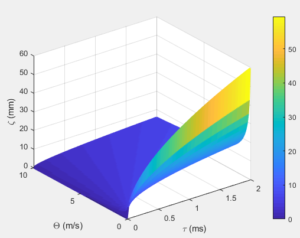
Figure 6 and Figure 7 describe the impact of half cone angle and density on spray penetration. When these parameters are augmented, the penetration capability of the two phase spray increases. These parameters can be used to control processed where high spray penetration is necessary in two phase fluid flow involving fuel droplet and entrained air

Figure 6. Effect of half liquid spray cone angle

Figure 7. Effect of density

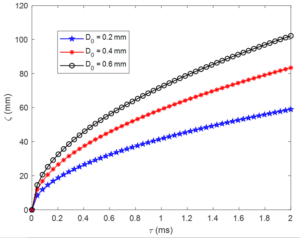
5.5. Effect of orifice diameter on spray penetration

Figure 8 explains the influence of orifice diameter on spray penetration. An increase in the orifice diameter causes the spray penetration to increase. This is due to the easy admittance of the spray with minimal restriction. However, when larger diameters are required with specified penetration values, the initial injection velocities may be controlled with the orifice diameter since the continuity equation must always be satisfied for the two phase fluid flow spray penetration process

Figure 8. Effect of orifice diameter

5.6. Dynamic impact of half cone angle and density on spray penetration

Figure 9 and Figure 10 display the dynamics of spray penetration considering the half cone angle and the droplet initial velocity. The dynamic plot can be used to monitor more than a variable at a time.

Figure 9. Dynamic impact of half cone angle

Table 1. Comparism and Validation of the analytical scheme.
\(\tau\) \(\stigma(\tau)\)
RKF45 Sazhin <i>et al.</i> [1]1} (Experiment) Jalipour <i>et al.</i> [1]12} (HPM) Present study (DTM
0.0 0.0000000000 0.0000000000 0.0000000000 0.0000000000
0.1 13.4494000600 13.4494000621 13.4494000611 13.4494000600
0.2 19.0203239700 19.0203239700 19.0203239700 19.0203239700
0.3 23.2950442300 23.2950442303 23.2950442301 23.2950442300
0.4 26.8988001100 26.8988001100 26.8988001100 26.8988001100
0.5 30.0737728000 30.0737728055 30.0737728042 30.0737728000
0.6 32.9441674900 32.9441674900 32.9441674900 32.9441674900
0.7 35.5837678400 35.5837678400 35.5837678400 35.5837678400
0.8 38.0406479300 38.0406479300 38.0406479300 38.0406479300
0.9 40.3482001800 40.3482001811 40.3482001801 40.3482001800
1.0 42.5307373500 42.5307373500 42.5307373500 42.5307373500
1.1 44.6066136500 44.6066136500 44.6066136500 44.6066136500
1.2 46.5900884700 46.5900884700 46.5900884700 46.5900884700
1.3 48.4925015400 48.4925015403 48.4925015402 48.4925015400
1.4 50.3230470900 50.3230470900 50.3230470900 50.3230470900
1.5 52.0893024300 52.0893024300 52.0893024300 52.0893024300
1.6 53.7976002300 53.7976002301 53.7976002302 53.7976002300
1.7 55.4532970300 55.4532970300 55.4532970300 55.4532970300
1.8 57.0609718900 57.0609718900 57.0609718900 57.0609718900
1.9 58.6245757000 58.6245757005 58.6245757007 58.6245757000
2.0 60.1475455600 60.1475455600 60.1475455600 60.1475455600

Figure 10. Dynamic impact of droplet initial velocity

Figure 11. Validation and Comparison of result

6. Conclusion

In this work, analysis has been performed on the generalized dynamics of two phase fuel spray penetration using differential transform method. The results of the DTM solution were verified, compared and validated. It was confirmed that DTM is an efficient method for the problem studied. Also, the parametric studies performed helps with the understanding of how the two phase spray penetration process can be properly monitored and controlled. The results show that an increase in the initial velocity and orifice diameter causes a corresponding increase in spray penetration while an antonymous effect is noticed for an increased semi cone angle and density. This work will find vital applications in the optimization of systems whose operation are influence by the aforementioned spray penetration process.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

The authors declare no conflict of interest.

References

  1. Sazhin, S. S., Feng, G., & Heikal, M. R. (2001). A model for fuel spray penetration. Fuel, 80(15), 2171-2180. [Google Scholor]
  2. Borman, G. L., & Ragland, K. W. (1998) Combustion engineering. New York: McGraw-Hill. [Google Scholor]
  3. Iyer, V. A., Abraham, J., & Magi, V. (2002). Exploring injected droplet size effects on steady liquid penetration in a Diesel spray with a two-fluid model. International Journal of Heat and Mass Transfer, 45(3), 519-531. [Google Scholor]
  4. Loth, E. (2000). Numerical approaches for motion of dispersed particles, droplets and bubbles. Progress in energy and combustion science, 26(3), 161-223. [Google Scholor]
  5. Pozorski, J., Sazhin, S., Waclawczyk, M., Crua, C., Kennaird, D., & Heikal, M. (2002). Spray penetration in a turbulent flow. Flow, Turbulence and Combustion, 68(2), 153. [Google Scholor]
  6. Faeth, G. M., Hsiang, L. P., & Wu, P. K. (1995). Structure and breakup properties of sprays. International Journal of Multiphase Flow, 21, 99-127. [Google Scholor]
  7. Ganji, D. D., & Khalegi, H. (2005). Effect of Nonlinear Turbulence Model on the Spray Performance in a Two-Phase Flow. Sharif Journal of Science and Technology, Iran, 29, 47-56. [Google Scholor]
  8. Ebrahimian, V., Ganji, D. D., & Esmaeipour, M. (2008). Variational Iteration Method to investigate the initial stage of fuel spray penetration. International Journal of Dynamics of Fluids, 4(2), 109-120. [Google Scholor]
  9. Bararnia, H., Ghasemi, E., Soleimani, S., Ghotbi, A. R., & Ganji, D. D. (2012). Solution of the Falkner-Skan wedge flow by HPM-Pade'method. Advances in Engineering Software, 43(1), 44-52. [Google Scholor]
  10. Mebine, P. (2012). A unified model for fuel spray penetration. Turkish Journal of Engineering and Environmental Sciences, 36(3), 219-225. [Google Scholor]
  11. Ghosh, S., & Hunt, J. C. R. (1994). Induced air velocity within droplet driven sprays. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 444(1920), 105-127. [Google Scholor]
  12. Jalilpour, B., Jafarmadar, S., Ganji, D. D., & Rashidi, M. M. (2016). Solution of analytical model for fuel spray penetration via homotopy perturbation method. Propulsion and Power Research, 5(3), 202-210. [Google Scholor]
  13. Sobamowo, G., Adeleye, O., & Yinusa, A. (2017). Analysis of convective-radiative porous fin With temperature-dependent internal heat Generation and magnetic field using Homotopy Perturbation method. Journal of computational and Applied Mechanics, 12(2), 127-145. [Google Scholor]
  14. Sobamowo, G. M., & Yinusa, A. (2018). Transient Combustion Analysis for Iron Micro-Particles in a Gaseous Oxidizing Medium Using Adomian Decomposition Method. Journal of Computational Engineering and Physical Modeling, 1, 1-15. [Google Scholor]
  15. Sobamowo, G. M., & Yinusa, A. A. (2018). Transient combustion analysis of iron micro-particles in a gaseous oxidizing medium using a new iterative method. Journal of Computational and Engineering Mathematics, 5(3), 3-16. [Google Scholor]
  16. Yinusa, A. A., & Sobamowo., M. G. (2019). On The Transient Combustion Analysis for Iron Micro -particles in a Gaseous Oxidizing Medium Using Variational Iteration Method. Journal of Reliability Engineering and Resilience. 1(1), 01-12. [Google Scholor]
  17. Yinusa, A., & Sobamowo, G. (2019). Analysis of Dynamic Behaviour of a Tensioned Carbon Nanotube in Thermal and Pressurized Environments. Karbala International Journal of Modern Science, 5(1), 2. [Google Scholor]
  18. Hikmah, S. N., Zubaidah, S. S., Sabrina, A. M. N., Kholijah, A. M. S., Rohaida, C. M., Shalyda, M. S., ... & Rafiziana, M. K. (2019). Preliminary study on the tea dust explosion: the effect of tea dust size. In MATEC Web of Conferences (Vol. 255, p. 02014). EDP Sciences. [Google Scholor]
  19. Sobamowo, M. G., Yinusa, A. A., & Oluwo, A. A. (2018). Slip analysis of magnetohydrodynamics flow of an upper-convected Maxwell viscoelastic nanofluid in a permeable channel embedded in a porous medium. Aeron Aero Open Access J, 2(5), 310-318. [Google Scholor]
  20. Chamkha, A. (2011). Application of multi-step differential transform method on flow of a second-grade fluid over a stretching or shrinking sheet. American Journal of Computational Mathematics, 6, 119-128. [Google Scholor]
  21. Sobamowo, M. G., & Yinusa, A. A. (2018). Thermo-Fluidic Parameters Effects on Nonlinear Vibration of Fluid-Conveying Nanotube Resting on Elastic Foundations using Homotopy Perturbation Method. Journal of Thermal Engineering, 4(8), 2211-2233. [Google Scholor]
  22. Sobamowo, M. G., Oguntala, G. A., & Yinusa, A. A. (2019). Nonlinear Transient Thermal Modeling and Analysis of a Convective-Radiative Fin with Functionally Graded Material in a Magnetic Environment. Modelling and Simulation in Engineering, 2019, 1-16. [Google Scholor]
  23. Sobamowo, M. G., Jayesimi, L., Oke, D., Yinusa, A. A., & Adedibu. O. (2019). Unsteady casson nanofluid squeezing flow between two parallel plates embedded in a porous medium under the influence of magnetic field. Open Journal of Mathematical Science, 3, 59 – 73. [Google Scholor]
  24. Odibat, Z. M., Bertelle, C., Aziz-Alaoui, M. A., & Duchamp, G. H. (2010). A multi-step differential transform method and application to non-chaotic or chaotic systems. Computers \& Mathematics with Applications, 59(4), 1462-1472. [Google Scholor]
Category: EASL - Vol 2 - Issue 4 (2019)