Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2020.0036
Leap Zagreb and leap hyper-Zagreb indices of Jahangir and Jahangir derived graphs
Fatima Asif, Zohaib Zahid\(^1\), Sohail Zafar
Department of Mathematics, University of Management and Technology, Lahore Pakistan.; (F.A & Z.Z & S.Z)
Abstract
Keywords:
1. Introduction
Chemical graph theory, a branch of mathematical chemistry, applies graph theory to mathematical modeling of chemical phenomena. Topological indices are real numbers that are presented as graph parameters (e.g. the degree of vertices, distances, etc.) introduced during studies conducted on the molecular graphs in chemistry and can describe some physical and chemical properties of molecules.
Let \(G\) be a simple and connected graph with order \(V(G)\) and size \(E(G)\subseteq V(G) \times V(G)\). The degree \(d_u\) of any vertex \(u\) is defined as the number of vertices joined to that vertex \(u\). The distance between two vertices \(u\) and \(v\) of a graph \(G\) is the number of edges in a shortest path connecting them and is denoted by \(d(u, v)\). The subdivision graph \(S(G)\) is a graph resulting from the subdivision of all the edges of \(G\). The line graph \(L(G)\) of a graph \(G\) whose vertices are the edges of \(G\), with \(uv\in E(L(G))\) when \(u\) and \(v\) have a common end point in \(G\). In structural chemistry, line graph of a graph \(G\) is very useful. The first topological indices on the basis of line graph was introduced by Bertz in 1981 (see [1]). The topological indices of Jahangir graph and its line graph are computed by many researchers (see [2, 3, 4, 5]).
For a vertex \(v\) in \(G\), the open \(k-\)neighborhood of \(v\) is defined as \(N_{k}(v/G) = \{u \in V(G): d(u, v) = k\}\), where \(k\) is a positive integer. The \(k-\)distance degree, denoted by \(d_{k}(v/G)\), of a vertex \(v \in V(G)\) is the number of \(k-\)neighbors of \(v\) in \(G\), \(i.e.,\) \(d_k(v/G) = |N_k(v/G)|\). It is clear that \(d_1(v/G) = d_v\) for every \(v \in V(G)\). The \(2-\)distance degree of a vertex \(v\) consists of all vertices at distance two to \(v\).
Recently, leap Zagreb indices of a graph have been introduced by Naji et al., (see [6]), depending on \(2-\)distance degree of the vertices. The leap Zagreb indices have several chemical applications. The first leap Zagreb index has very good correlation with physical properties of chemical compounds like boiling point, entropy, \(DHVAP\), \(HVAP\) and accentric factor (see [7]). Shiladhar et al., computed leap Zagreb indices of some wheel related graphs (see [8]). For more details about leap indices, see [9, 10, 11, 12].
For a graph \(G\), the first, second, and third leap Zagreb indices are defined as:2. Leap Zagreb and leap hyper-Zagreb indices of Jahangir graph \(J_{n,m}\)
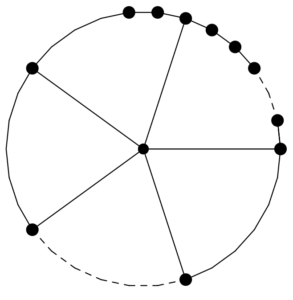
In this section, we will compute leap Zagreb indices and hyper-leap Zagreb indices of Jahangir graph \(J_{n,m}\). The Jahangir graph \(J_{n,m}\) consists of a cycle \(C_{nm}\) with one additional vertex which is adjacent to \(m\) vertices of \(C_{nm}\) at distance to each other [16].Figure 1. The Jahangir graph \(J_{n,m}\).
Theorem 1. Let \(J_{n,m}\) be the Jahangir graph, then
- \(LM_1(J_{n,m})=m^3+6m^2+4mn+7m\).
- \(LM_2(J_{n,m})=2m^3+8m^2+4mn+2m\).
- \(LM_3(J_{n,m})=5m^2+4mn+3m.\)
- \(HLM_1(J_{n,m})=11m^3+22m^2+16mn+19m.\)
- \(HLM_2(J_{n,m})=4m^5+8m^4+22m^3+36m^2+16mn+26m.\)
Proof. Let \(J_{n,m}\) be a Jahangir graph with \(m(n+1)\) edges and \(mn+1\) vertices as shown in Figure 1. For an edge \(uv \in E(J_{n,m})\), the \(2-\)distance degree of a vertex \(u\) and vertex \(v\) is denoted by \(d_2(u/J_{n,m})\) and \(d_2(v/J_{n,m})\) respectively. The edge partition of \(J_{n,m}\) with respect to \(2-\)distance degree of vertices of \(J_{n,m}\) is shown in Table 1. The vertex partition of graph \(J_{n,m}\) based on the \(1-\)distance degree of a vertex \(u\) and \(2-\)distance degree of a vertex \(u\) is shown in Table 2.
Table 1. The edge partition of \(J_{n,m}\), where \(d_2(u/J_{n,m})d_2(v/J_{n,m})\) \(\in E(J_{n,m})\).
| No. of edges | \(d_2(u/J_{n,m})\) | \(d_2(v/J_{n,m})\) |
|---|---|---|
| \(m(n-4)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(2m\) | \(3\) | \(m+1\) |
| \(m\) | \(2m\) | \(m+1\) |
Table 2. The vertex partition of \(J_{n,m}\) where \(d_1(v/J_{n,m})\), \(d_2(v/J_{n,m})\) \(\in V(J_{n,m})\).
| No. of vertices | \(d_1(v/J_{n,m})\) | \(d_2(v/J_{n,m})\) |
|---|---|---|
| \(1\) | \(m\) | \(2m\) |
| \(m(n-3)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(m\) | \(3\) | \(m+1\) |
- Using Formula (1) and Table 2, we have \begin{eqnarray*} LM_1(J_{n,m})&=&1.(2m)^2+m(n-3)(2)^2+2m(3)^2+m(m+1)^2\\ &=&m^3+6m^2+4mn+7m. \end{eqnarray*}
- Using Formula (2) and Table 1, we have \begin{eqnarray*} LM_2(J_{n,m})&=&m(n-4)(2.2)+2m(2.3)+2m(3.(m+1))+m(2m.(m+1))\\ &=&2m^3+8m^2+4mn+2m. \end{eqnarray*}
- Using Formula (3) and Table 2, we have \begin{eqnarray*} LM_3(J_{n,m})&=&1.(2m.m)+m(n-3)(2.2)+m(3.(m+1))+2m(3.2)\\ &=&5m^2+4mn+3m. \end{eqnarray*}
- Using Formula (4) and Table 1, we have \begin{eqnarray*} HLM_1(J_{n,m})&=&m(n-4)(2+2)^2+2m(2+3)^2+2m(3+(m+1))^2+m(2m+(m+1))^2\\ &=&11m^3+22m^2+16mn+19m. \end{eqnarray*}
- Using Formula (5) and Table 1, we have \begin{eqnarray*} HLM_2(J_{n,m})&=&m(n-4)(2.2)^2+2m(2.3)^2+2m(3.(m+1))^2+m(2m.(m+1))^2\\ &=&4m^5+8m^4+22m^3+36m^2+16mn+26m. \end{eqnarray*}
3. Leap Zagreb and leap hyper-Zagreb indices of the line graph of Jahangir graph \(J_{n,m}\)
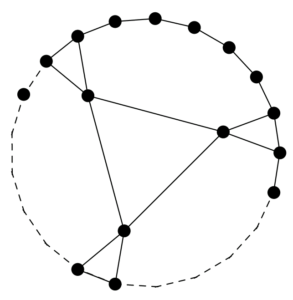
In this section, we will compute leap Zagreb indices and hyper-leap Zagreb indices of the line graph of Jahangir graph \(J_{n,m}\).Figure 2. The line graph of Jahangir graph \(J_{n,m}\)
Theorem 2. Let \(L(J_{n,m})\) be the line graph of the Jahangir graph \(J_{n,m}\), then
- \(LM_1(L(J_{n,m}))=m^3+2m^2+4mn+11m\).
- \(LM_2(L(J_{n,m}))=2m^4+3m^3+12m^2+4mn-m\).
- \(LM_3(L(J_{n,m}))=2m^3+8m^2+4mn+2m\).
- \(HLM_1(L(J_{n,m}))=8m^4+13m^3+30m^2+16mn+5m\).
- \(HLM_2(L(J_{n,m}))=8m^6+16m^4+27m^3+38m^2+16mn+11m\).
Proof. Let \(L(J_{n,m})\) be a line graph of Jahangir graph \(J_{n,m}\) with \(\frac{m^2+2mn+3m}{2}\) edges and \(m(n+1)\) vertices is shown in Figure 2. For an edge \(uv \in E(L(J_{n,m}))\), the \(2\)-distance degree of a vertex \(u\) and vertex \(v\) is denoted by \(d_2(u/L(J_{n,m}))\) and \(d_2(v/L(J_{n,m}))\) respectively. The edge partition of \(L(J_{n,m})\) with respect to \(2\)-distance degree of vertices of \(L(J_{n,m})\) is shown in Table 3. The vertex partition of graph \(L(J_{n,m})\) based on the \(1\)-distance degree of a vertex \(u\) and \(2\)-distance degree of a vertex \(u\) is shown in Table 4.
Table 3. The edge partition of \(L(J_{n,m})\), where \(d_2(u/L(J_{n,m}))d_2(v/L(J_{n,m}))\) \(\in\) \(E(L(J_{n,m}))\).
| Number of edges | \(d_2(u/L(J_{n,m}))\) | \(d_2(v/L(J_{n,m}))\) |
|---|---|---|
| \(m(n-5)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(m\) | \(3\) | \(3\) |
| \(2m\) | \(3\) | \(m+1\) |
| \(\frac{m(m-1)}{2}\) | \(m+1\) | \(m+1\) |
Table 4. The vertex partition of \(L(J_{n,m})\) where \(d_1(v/L(J_{n,m}))\), \(d_2(v/L(J_{n,m}))\) \(\in V(L(J_{n,m}))\).
| No. of \(1-\)distance degree vertices | \(d_1(u/L(J_{n,m}))\) | No. of \(2-\)distance degree vertices | \(d_2(u/L(J_{n,m}))\) |
|---|---|---|---|
| \(m(n-4)\) | \(2\) | \(m(n-4)\) | \(2\) |
| \(2m\) | \(2\) | \(2m\) | \(3\) |
| \(2m\) | \(3\) | \(m\) | \(2m\) |
| \(m\) | \(m+1\) | \(2m\) | \(m+1\) |
- Using Formula (1) and Table 4, we have \begin{eqnarray*} LM_1(L(J_{n,m}))&=&m(n-4)(2)^2+2m(2)^2+2m(3)^2+m(m+1)^2\\ &=&m^3+2m^2+4mn+11m. \end{eqnarray*}
- Using Formula (2) and Table 3, we have \begin{eqnarray*} LM_2(L(J_{n,m}))&=&m(n-5)(2.2)+2m(2.3)+2m(3.(m+1))+m(m+1)^2+2m(2m.(m+1))\\&&+\frac{m(m-1)}{2}(2m.2m)\\ &=&2m^4+3m^3+12m^2+4mn-m. \end{eqnarray*}
- Using Formula (3) and Table 4, we have \begin{eqnarray*} LM_3(L(J_{n,m}))&=&m(n-4)(2.2)+m.(2m.(m+1))+2m(3.(m+1))+2m(3.2)\\ &=&2m^3+8m^2+4mn+2m. \end{eqnarray*}
- Using Formula (4) and Table 3, we have \begin{eqnarray*} HLM_1(L(J_{n,m}))&=&m(n-5)(2+2)^2+2m(2+3)^2+2m(3+(m+1))^2+m(m+1)^2\\&&+2m(2m+(m+1))^2+\frac{m(m-1)}{2}(2m+2m)^2\\ &=&8m^4+13m^3+30m^2+16mn+5m. \end{eqnarray*}
- Using Formula (5) and Table 3, we have \begin{eqnarray*} HLM_2(L(J_{n,m}))&=&m(n-5)(2.2)^2+2m(2.3)^2+2m(3.(m+1))^2+m(m+1)^2\\&&+2m(2m.(m+1))^2+\frac{m(m-1)}{2}(2m.2m)^2\\ &=&8m^6+16m^4+27m^3+38m^2+16mn+11m. \end{eqnarray*}
4. Leap Zagreb and leap-hyper Zagreb indices of the subdivision of Jahangir Graph \(J_{n,m}\)
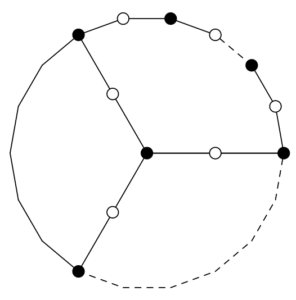
In this section, we will compute leap Zagreb indices and hyper-leap Zagreb indices of the subdivision of Jahangir graph \(J_{n,m}\).Figure 3. The subdivision of Jahangir graph \(J_{n,m}\)
Theorem 3. Let \(S(J_{m,n})\) be the subdivision graph of the Jahangir graph \(J_{m,n}\), then
- \(LM_1(S(J_{n,m}))=m^3+3m^2+8mn+16m\).
- \(LM_2(S(J_{n,m}))=m^3+4m^2+8mn+17m \).
- \(LM_3(S(J_{n,m}))=3m^2+4mn+11m\).
- \(HLM_1(S(J_{n,m}))=5m^3+12m^2+32mn+75m\).
- \(HLM_2(S(J_{n,m}))=m^5+2m^4+10m^3+18m^2+32mn+179m\).
Proof. Let \(S(J_{n,m})\) be a subdivision of Jahangir graph with \(2m(n+1)\) edges and \(m(2n+1)+1\) vertices is shown in Figure 3. For an edge \(uv \in E(S(J_{n,m}))\), the \(2-\)distance degree of a vertex \(u\) and vertex \(v\) is denoted by \(d_2(u/S(J_{n,m}))\) and \(d_2(v/S(J_{n,m}))\) respectively. The edge partition of \(E(S(J_{n,m}))\) with respect to \(2-\)distance degree of a vertex \(u\) in \(S(J_{n,m})\) is shown in Table 5. The vertex partition of graph \(S(J_{n,m})\) based on the \(1-\)distance degree of a vertex \(u\) and \(2-\)distance degree of a vertex \(u\) is shown in Table 6. \begin{table}[H] \centering
Table 5. The edge partition of \(S(J_{n,m})\), where \(d_2(u/S(J_{n,m}))d_2(v/S(J_{n,m}))\) \(\in E(S(J_{n,m}))\).
| No. of edges | \(d_2(u/S(J_{n,m}))\) | \(d_2(v/S(J_{n,m}))\) |
|---|---|---|
| \(2m(n-2)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(2m\) | \(3\) | \(3\) |
| \(m\) | \(3\) | \(m+1\) |
| \(m\) | \(m\) | \(m+1\) |
Table 6. The vertex partition of \(S(J_{n,m})\), where \(d_1(v/S(J_{n,m}))\), \(d_2(v/S(J_{n,m}))\) \(\in V(S(J_{n,m}))\).
| No. of vertices | \(d_1(v/S(J_{n,m}))\) | \(d_2(v/S(J_{n,m}))\) |
|---|---|---|
| \(1\) | \(m\) | \(m\) |
| \(m(2n-3)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(m\) | \(2\) | \(3\) |
| \(m\) | \(3\) | \(m+1\) |
- Using Formula (1) and Table 6, we have \begin{eqnarray*} LM_1[S(J_{n,m})]&=&1.(m)^2+m(2n-3)(2)^2+2m(3)^2+m(3)^2+m(m+1)^2\\ &=&m^3+3m^2+8mn+16m. \end{eqnarray*}
- Using Formula (2) and Table 5, we have \begin{eqnarray*} LM_2[S(J_{n,m})]&=&2m(n-2)(2.2)+2m(2.3)+2m(3.3)+m(3.(m+1))+m(m.(m+1))\\ &=&m^3+4m^2+8mn+17m. \end{eqnarray*}
- Using Formula (3) and Table 6, we have \begin{eqnarray*} LM_3[S(J_{n,m})]&=&1.(m.m)+m(n-3)(2.2)+2m(2.3)+m(3.3)+m(2.(m+1))\\ &=&3m^2+4mn+11m. \end{eqnarray*}
- Using Formula (4) and Table 5, we have \begin{eqnarray*} HLM_1[S(J_{n,m})]&=&2m(n-2)(2+2)^2+2m(2+3)^2+2m(3+3)^2+m(3+(m+1))^2+m(m+(m+1))^2\\ &=&5m^3+12m^2+32mn+75m. \end{eqnarray*}
- Using Formula (5) and Table 5, we have \begin{eqnarray*} HLM_2[S(J_{n,m})]&=&2m(n-2)(2.2)^2+2m(2.3)^2+2m(3.3)^2+m(3.(m+1))^2+m(m.(m+1))^2\\ &=&m^5+2m^4+10m^3+18m^2+32mn+179m. \end{eqnarray*}
5. Leap Zagreb and leap-hyper Zagreb indices of line graph of the subdivision of Jahangir graph \(J_{n,m}\)
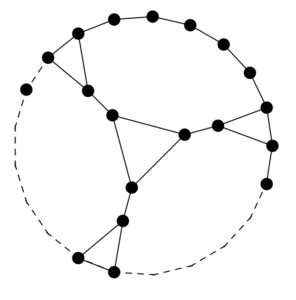
In this section, we will compute leap Zagreb indices and hyper-leap Zagreb indices of the line graph of the subdivision of Jahangir graph \(J_{n,m}\).Figure 4. The line graph of the subdivision of Jahangir graph \(J_{n,m}\).
Theorem 4. Let \(L[(S(J_{n,m}))]\) be the line graph of the subdivision of Jahangir graph \(J_{n,m}\), then
- \(LM_1[L(S(J_{n,m}))]=2m^3+4m^2+8mn+22m\).
- \(LM_2[L(S(J_{n,m}))]=\frac{1}{2}[m^4+3m^3+15m^2+8mn+51m]\).
- \(LM_3[L(S(J_{n,m}))]=m^3+4m^2+8mn+17m\).
- \(HLM_1[L(S(J_{n,m}))]=\frac{1}{2}[4m^4+16m^3+44m^2+64mn+224m]\).
- \(HLM_2[L(S(J_{n,m}))]=\frac{1}{2}[m^6+5m^5+10m^4+46m^3+77m^2+64mn+507m]\).
Proof. Let \(L(S(J_{n,m}))\) be the line graph of the subdivision of Jahangir graph \(J_{n,m}\) with \(\frac{m^2+4mn+5m}{2}\) edges and \(2m(n+1)\) vertices is shown in Figure 4. For an edge \(uv \in E[L(S(J_{n,m}))]\), the \(2-distance\) degree of a vertex \(u\) and vertex \(v\) is denoted by \(d_2(u/L(S(J_{n,m})))\) and \(d_2(v/L(S(J_{n,m})))\) respectively. The edge partition of \(E[L(S(J_{n,m}))]\) with respect to \(2-\)distance degree of a vertex \(u\) in \(L(S(J_{n,m}))\) is shown in Table 7. The vertex partition of graph \(L(S(J_{n,m}))\) based on the \(1-\)distance degree of a vertex \(u\) and \(2-\)distance degree of a vertex \(u\) is shown in Table 8.
Table 7. The edge partition of \(L(S(J_{n,m}))\), where \(d_2(u/L(S(J_{n,m})))d_2(v/L(S(J_{n,m})))\) \(\in E(L(S(J_{n,m})))\).
| No. of edges | \(d_2(u/L(S(J_{n,m})))\) | \(d_2(v/L(S(J_{n,m})])\) |
|---|---|---|
| \(m(2n-5)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(3m\) | \(3\) | \(3\) |
| \(2m\) | \(3\) | \(m+1\) |
| \(\frac{m(m+1)}{2}\) | \(m+1\) | \(m+1\) |
Table 8. The vertex partition of \(L[S(J_{n,m})]\), where \(d_1(u/L(S(J_{n,m})))\), \(d_2(u/L(S(J_{n,m})))\) \(\in V(L(S(J_{n,m})))\).
| No. of vertices | \(d_1(u/L(S(J_{n,m})))\) | \(d_2(u/L(S(J_{n,m})))\) |
|---|---|---|
| \(2m(n-2)\) | \(2\) | \(2\) |
| \(2m\) | \(2\) | \(3\) |
| \(2m\) | \(3\) | \(3\) |
| \(m\) | \(3\) | \(m+1\) |
| \(m\) | \(m\) | \(m+1\) |
- Using Formula (1) and Table 8, we have \begin{eqnarray*} LM_1[L(S(J_{n,m}))]&=&4m(3)^2+2m(n-2)(2)^2+2m(m+1)^2\\ &=&2m^3+4m^2+8mn+22m. \end{eqnarray*}
- Using Formula (2) and Table 7, we have \begin{eqnarray*} LM_2[L(S(J_{n,m}))] &=&m(2n-5)(2)^2+2m(2.3)+3m(3)^2+2m(3.(m+1))+\frac{m(m+1)^3}{2}\\ &=&\frac{1}{2}[m^4+3m^3+15m^2+8mn+51m]. \end{eqnarray*}
- Using Formula (3) and Table 8, we have \begin{eqnarray*} LM_3[L(S(J_{n,m}))]&=&2m(n-2)(2.2)+2m(2.3)+2m(3.3)+m(3.(m+1))+m(m.(m+1))\\ &=&m^3+4m^2+8mn+17m. \end{eqnarray*}
- Using Formula (4) and Table 7, we have \begin{eqnarray*} HLM_1[L(S(J_{n,m}))]&=&m(2n-5)(2+2)^2+2m(2+3)^2+3m(3+3)^2+2m(3+(m+1))^2\\ &&+\frac{m(m+1)}{2}[(m+1)+(m+1)]^2\\ &=&\frac{1}{2}[4m^4+16m^3+44m^2+64mn+224m]. \end{eqnarray*}
- Using Formula (5) and Table 7, we have \begin{eqnarray*} HLM_2[L(S(J_{n,m}))] &=&m(2n-5)(2.2)^2+2m(2.3)^2+3m(3.3)^2+2m(3.(m+1))^2\\ &&+\frac{m(m+1)}{2}[(m+1).(m+1)]^2\\ &=&\frac{1}{2}[m^6+5m^5+10m^4+46m^3+77m^2+64mn+507m]. \end{eqnarray*}
Autho Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflict of Interests
The authors declare no conflict of interest.References
- Bertz, S. H. (1981). The bond graph. Journal of the Chemical Society, Chemical Communications, 1981, 818-820.
- Farahani, M. R., & Gao, W. (2015). The Schultz index and Schultz polynomial of the Jahangir Graphs \(J_{5, m}\). Applied mathematics, 6(14), 2319-2325.[Google Scholor]
- Farahani, M. R., Kanna, R., & Gao, W. (2015). The Schultz, Modified Schultz indices and their polynomials of the Jahangir graphs \(J_{n, m}\) for integer numbers \(n= 3, m\geq3\). Asian Journal of Applied Sciences, 3(6) (2015), 823-827.[Google Scholor]
- Munir, M., Nazeer, W., Kang, S. M., Qureshi, M. I., Nizami, A. R., & Kwun, Y. C. (2017). Some invariants of Jahangir graphs. Symmetry, 9(1), 17.[Google Scholor]
- Wang, S., Farahani, M. R., Kanna, M. R., Jamil, M. K., & Kumar, R. P. (2016). The Wiener Index and the Hosoya Polynomial of the Jahangir Graphs. Applied and Computational Mathematics, 5(3), 138-141.[Google Scholor]
- Gutman, I., Naji, A. M., & Soner, N. D. (2017). On leap Zagreb indices of graphs. Communication in Combinatorics and Optimization, 2(2), 99-117.[Google Scholor]
- Basavanagoud, B., & Jakkannavar, P. (2018). Computing first leap Zagreb index of some nano structures. International Journal of Mathematics and its Applications, 6(2), 141-150.[Google Scholor]
- Shiladhar, P., Naji, A. M., & Soner, N. D. (2018). Computation of leap Zagreb indices of some windmill graphs. International Journal of Mathematics and its Applications, 6(2), 183-191.[Google Scholor]
- Manjunathe, H. R., Naji, A. M., Shiladhar, P., & Soner, N. D. (2019). Leap eccentric connectivity index of some graph operations. International Journal of Research and Analytical Reviews, 6, 882-887.[Google Scholor]
- Naji, A. M., & Soner, N. D. (2018). The first leap Zagreb index of some graph operations. International Journal of Applied Graph Theory, 2(1), 7-18.[Google Scholor]
- Naji, A. M., Soner, N. D., & Gutman, I. (2017). The first leap zagreb index of some graph opertations. Communications in Combinatorics and Optimization, 3(2), 179-194.[Google Scholor]
- Soner, N. D., & Naji, A. M. The k-distance neighborhood polynomial of a graph, World Academy Sci. Engin. Tech. In Conference Proceedings, San Francico, USA, Sep (pp. 26-27).[Google Scholor]
- Kulli, V. R. (2018). Leap hyper-Zagreb indices and their polynomials of certain graphs. International Journal of Current Research in Life Sciences, 7(10), 2783-2791.[Google Scholor]
- Basavanagoud, B., & Chitra, E. (2018). On leap hyper-Zagreb indices of some nanostructures. International Journal of Mathematics Trends and Technology, 64(1), 30-36.[Google Scholor]
- Kulli, V. R., Jakkannavar, P., & Basavanagoud, B. (2019). Computation of leap hyper-Zagreb indices of certain windmill graphs. Int. J. Sci. Res. in Mathematical and Statistical Sciences, 6(2), 75-79.[Google Scholor]
- Ali, K., Baskoro, E. T., & Tomescu, I. (2008). On the Ramsey numbers for paths and generalized Jahangir graphs \(J_{s, m}\). Bulletin mathématique de la Société des Sciences Mathématiques de Roumanie, 177-182.[Google Scholor]