Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2020.0050
Transient free convection heat and mass transfer of Casson nanofluid over a vertical porous plate subjected to magnetic field and thermal radiation
M. G. Sobamowo
Department of Mechanical Engineering, University of Lagos, Akoka, Lagos State, Nigeria.; mikegbeminiyi@gmail.com
Abstract
Keywords:
1. Introduction and Preliminaries
Free convection flow over vertical surfaces has been widely applied in different engineering areas such as mechanical forming processes, glass-fibre production processes, extrusion, food processing, melt spinning etc. Consequently, this has aroused lots of research interests on the flow phenomena following the experimental investigations of Schmidt and Beckmann [1] and the pioneering theoretical work of Ostrach et al. [2]. An extended work was done by Sparrow and Gregg [3] on the free convection under the influence of a uniform surface heat flux. In another work, Cianfrini et al. [4] studied the flow phenomena over a non-isothermal vertical plate. Lefevre [5] examined the free convection of an inviscid flow under low Prandtl-numbers while Stewartson and Jones [6] as well as Eshghy [7] analyzed the flow over a heated vertical plate at high Prandtl number. Although, Roy [8] also studied the free convection flow process under a large Prandtl number, the effects of uniform surface heat flux on the flow phenomena was also investigated. Kuiken [9,10] and Kuiken and Rotem [11] examined the free convection flow over the vertical plates at both low and high Prandtl numbers. In recent times, different analytical and numerical methods have been used to examine the laminar free convection [12,13,14,15,16,17,18]. Also, various parametric studies on the nonlinear models and fluid flow problems have been presented in literature [19,20,21,22,23,24,25,26,27].
Different types of fluid such as tomato sauce, honey, printing inks, blood, concentrated fruit juices and Jelly have been classified as the non-Newtonian fluids called Casson fluids [28]. These fluids exhibit shear thinning nature with an assumed infinite viscosity at zero rate of shear, a yield stress below which no flow occurs, and a zero viscosity at an infinite rate of shear [29]. Its important areas of applications have provoked some studies [30,31]. Also, the effects of thermal radiation, magnetic field and nanoparticles on the fluid flow processes have been extensively studied [32,33,34,35,36,37,38,39,40]. However, most of these studies which are based on time invariant, focused on the free convection currents caused by the temperature difference. It should be stated that the flow is also affected by the differences in concentration on material constitution such as seen in atmospheric flows, chemical processing, formation and dispersion of fog, distributive temperature and moisture over agricultural fields. Also, the transient behaviours of the fluids flow before a steady state is reached should be well investigated. Hence, the study of the transient heat and mass transfer of the fluid over the vertical plate is very much important. Moreover, to the best of the authors knowledge, a study on transient behaviours of free convection boundary-layer flow, heat and mass transfer of Casson nanofluids over a vertical plate under the influences of thermal radiation, flow medium porosity and nanoparticles has not been presented in literature. Therefore, the transient magnetohydrodynamics free convection heat and mass transfer of Casson nanofluid past an isothermal vertical flat plate embedded in a porous media subjected to thermal radiation is investigated numerically using implicit finite difference scheme of Crank-Nicolson type. The numerical solutions are used to carry out parametric studies. The results are presented graphically and discussed.
2. Problem formulation and mathematical analysis
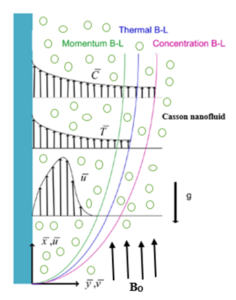
Consider a two-dimensional unsteady free-convection flow, heat and mass transfer of a Casson nanofluid over a vertical plate embedded in a porous media and parallel to the direction of the generating body force as shown in Figure 1.
Figure 1. Velocity, temperature and concentration profiles in free convection flow of a Casson fluid over a vertical plate.
In order to set up the flow, heat and mass transfer of the Casson nanofluid, the following assumptions are made
- 1. The flow is incompressible and laminar.
- 2. The heat transfer from the plate to the fluid is proportional to the local surface temperature.
- 3. Pressure is uniform across the boundary layer and Boussinesq approximation is used.
- 4. The thermal diffusion and diffusion thermal effects which are called the Soret and Dufour effects, respectively are insignificant and they are therefore negligible.
- 5. The effect of viscous dissipation on the fluid flow process is negligible.
- 6. There is no chemical reaction taking place in the mass of the fluid.
Table 1. The values of different shapes of nanoparticles [41, 42].
| Sr. No. | Name | Shape factor (m) | Sphericity($\psi$) |
|---|---|---|---|
| 1 | Sphere | 3.0 | 1.000 |
| 2 | Brick | 3.7 | 0.811 |
| 3 | Cylinder | 4.8 | 0.625 |
| 4 | Platelet | 5.7 | 0.526 |
| 5 | Lamina | 16.2 | 0.185 |
We now introduce the following non-dimensional quantities
3. Method of solution: finite difference method
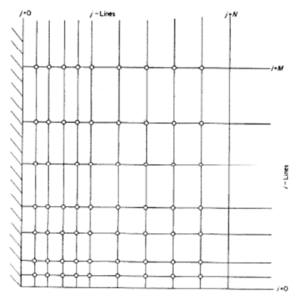
Indisputably, the finite difference method is one of the efficient methods of obtaining numerical solutions to differential equations. The difference scheme could be applied using explicit or implicit schemes. However, the applications of the finite difference scheme to the practical situations depict that the stability and convergence conditions for explicit finite-difference methods become extremely complicated coupled with high computational cost. In order to avoid obviate the inherent problems in the explicit schemes, implicit schemes are recommended. Such schemes permit large time-steps to be used with unconditional stability. Also, the use and the accuracy of finite difference method for the analysis of nonlinear problems has earlier been pointed out by Han et al. [43]. Therefore, in this work, implicit finite difference method of Crank-Nicolson type is used to discretize the systems of coupled non-linear ordinary differential equations combined with the initial and boundary conditions in governing Equations (21)-(24) as well as Equations (25)-(29), respectively. The finite difference forms for the systems of coupled non-linear ordinary differential equations, the initial and boundary conditions are given asThe implicit finite difference scheme is used for the Cartesian coordinate. The rectangular region of the integration (Figure 2) considered varies from 0 to 1 and y varying from 0 to 15. It is taken in this study that \(y_{max}\) lies well outside the momentums, energy and concentration boundary layers. It should be pointed out that after some preliminary investigations, the maximum of \(y\) was chosen as 15. This value is arrived at in order to make the boundary conditions in Equations (25) and (26) to be satisfied within the tolerance limit of \(10^{-5}\). For the rectangular region considered, the \(x\)- and \(y\)-directions are divided into \(M\) and \(L\) grid spacings, respectively as shown in Figure 2. In order to reduce the computational time, variable mesh sizes are used in the \(x\)- and \(y\)-directions as follows
Figure 2. The finite difference space grid for a non-uniform grid system.
It should be stated that the subscripts \(i\) designates the grid points with \(x\)-direction while \(j\) designates the grid points \(y\)-direction as shown in Figure 2. The superscript \(n\) represents a value of time in \(t\)-direction. The velocity, temperature and concentration distributions at all interior nodal points are computed by successive applications of the above finite difference equations (30)-(32) along with the initial and boundary conditions (33) - (37). The process of the computations is explained below.
From the initial conditions (33) - (37), the initial values (at \(t = 0\)) of \(u\), \(v\), \(T\) and \(C\) are known at all grid points. For the subsequent computations, it should be stated that during any one-time step, the coefficients appearing in the finite difference equations are treated as constants. Using the known values at previous time level \((n)\), the computations of \(u,\ v,\ T,\) and \(C\) at time level \((n + 1)\) are calculated as follows:
At every internal nodal point on a particular \(i-\) level, the finite difference equation (32) constitutes a tri-diagonal system of equations which is solved by Thomas algorithm as explained by Carnahan et al. [44]. Therefore, the values of \(C\) are determined at every nodal point on a particular \(i-\)level at \((n+ 1)th\) time level. In the same way, the values of \(T\) are computed using the finite difference Equation (31). Substituting the values of \(C\) and \(T\) at \((n +1)th\) time level in the finite difference Equation (30), the values of \(u\) at (\(n+ 1)th\) time level are found. Having determined the values of \(C\), \(T\) and \(u\) on a particular \(i-\)level, with the aid of the finite difference Equation (30) at every nodal point on a particular \(i-\)level at \((n +1)th\) time level, the values of \(v\) are calculated explicitly. This process is repeated for various \(i-\)levels. Thus, the values of \(C\), \(T\), \(u\) and \(v\) are known at all grid points in the rectangular region at \((n+ 1)th\) time level. The computations are carried out till the steady state is reached. In this present study, it is assumed that the steady state solution is reached, when the absolute difference between the values of \(u\), \(T\) and \(C\) at two consecutive time steps are less than \(10-5\) at all grid points.
4. Flow, heat and mass transfer parameters of engineering interests
In addition to the determination of the velocity, temperature and concentration distributions, it is often desirable to compute other physically important quantities (such as shear stress, drag, heat transfer and mass transfer rates) associated with the free convection flow, heat transfer and mass transfer problems. Consequently, flow, heat and mass transfer parameters are computed.4.1. Fluid flow parameter
The local skin-friction are derived as4.2. Heat transfer parameter
The local Nusselt number are given as4.3. Mass transfer parameter
The Sherwood are developed as5. Results and discussion
The results of the simulations are presented in this section and the effects of the various model parameters are presented.5.1. Effects of Casson parameter on the fluid velocity, temperature and concentration distributions
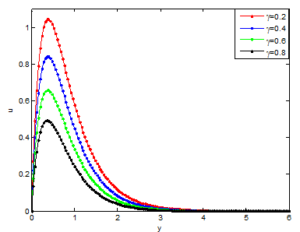
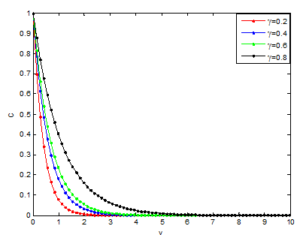
The effects of Casson parameter on the flow velocity, temperature and concentrations profiles of the nanofluid are shown in Figures 3, 4 and 5, respectively. The figures depict that the flow velocity of the nanofluid near the plate decreases as the Casson parameter increases as illustrated in Figure 3 The trend in the figure could explained that, physically, increasing values of Casson parameter develop the viscous forces which in consequent retards the flow of the and thereby reduced the flow velocity. It could be established from the results that the temperature as well as the concentration of the fluid increase as the Casson fluid parameter increase as shown in Figures 4 and 5.Figure 3. Effects of Casson parameter on the velocity profile of the Casson nanofluid
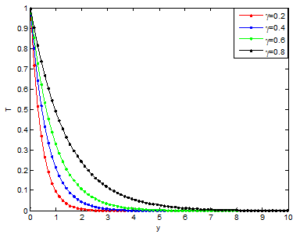
Figure 4. Effects of Casson parameter on temperature profile of the Casson nanofluid
Figure 5. Effects of Casson parameter on concentration profile Of the Casson nanofluid
5.2. Effects of radiation parameter on the fluid velocity, temperature and concentration distributions
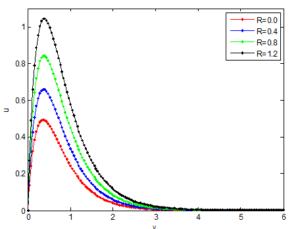
Figures 6, 7 and 8 show that the viscous, thermal and concentration boundary layers increase with the increase of radiation parameter, \(R\). It is shown that increase in radiation parameter causes the velocity of the fluid to increase. This is because as the radiation parameter is increased, the absorption of radiated heat from the heated plate releases more heat energy released to the fluid and the resulting temperature increases the buoyancy forces in the boundary layer which also increases the fluid motion and the momentum boundary layer thickness accelerates. This is expected, because the considered radiation effect within the boundary layer increases the motion of the fluid which increases the surface frictions.Figure 6. Effects of radiation parameter on the velocity profile of the Casson nanofluid
Figure 7. Effects of radiation parameter on temperature profile of the Casson nanofluid
Figure 8. Effects of radiation parameter on concentration profile of the Casson nanofluid
5.3. Effects of nanoparticle shape on the fluid velocity, temperature and concentration
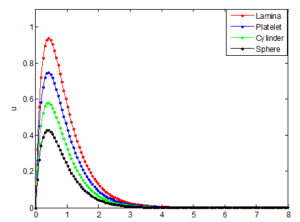
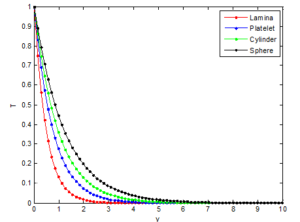
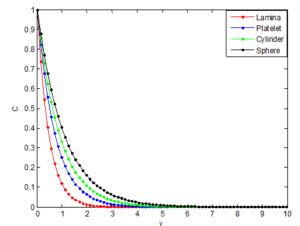
The use of nanoparticles in the fluids exhibited better properties relating to the heat transfer of fluid than heat transfer enhancement through the use of suspended millimeter- or micrometer-sized particles which potentially cause some severe problems, such as abrasion, clogging, high pressure drop, and sedimentation of particles. The very low concentrations applications and nanometer sizes properties of nanoparticles in basefluid prevent the sedimentation in the flow that may clog the channel. It should be added that the theoretical prediction of enhanced thermal conductivity of the basefluid and prevention of clogging, abrasion, high pressure drop and sedimentation through the addition of nanoparticles in basefluid have been supported with experimental evidences in literature.Figures 9, 10 and 11 show the influence of the shape of nanoparticle on the flow velocity, temperature and concentrations profiles of the nanofluid. It is observed that lamina shaped nanoparticle carries maximum velocity whereas spherical shaped nanoparticle has better enhancement on heat transfer than other nanoparticle shapes. In fact, it is in accordance with the physical expectation since it is well known that the lamina nanoparticle has greater shape factor than other nanoparticles of different shapes, therefore, the lamina nanoparticle comparatively gains maximum temperature than others. The velocity decrease is maximum in spherical nanoparticles when compared with other shapes. The enhancement observed at lower volume fractions for non-spherical particles is attributed to the percolation chain formation, which perturbs the boundary layer and thereby increases the local Nusselt number values. The results show that the maximum decrease in velocity and maximum increase in temperature are caused by lamina, platelets, cylinder and sphere, respectively. It is also observed that irreversibility process can be reduced by using nanoparticles, especially the spherical particles. This can potentially result in higher enhancement in the thermal conductivity of a nanofluid containing elongated particles compared to the one containing spherical nanoparticle, as exhibited by the experimental data in the literature. It is therefore required that that proper choice of nanoparticles should made as this will be helpful in controlling fluid flow, heat and mass transfer processes.
Figure 9. Effect of nanoparticle shape on velocity distribution of the nanofluid
Figure 10. Effects of nanoparticle shape on temperature distribution of nanofluid
Figure 11. Effects of nanoparticle shape on concentration distribution
5.4. Effect of Prandtl number on the fluid velocity, temperature and concentration distributions
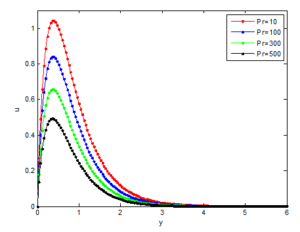
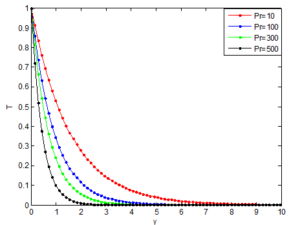
The figures also show the effects of Prandtl number (Pr) on the velocity and temperature profiles are shown in Figures 12, 13 respectively. It is indicated that the velocity of the Casson nanofluid decreases as the Pr increases but the temperature of the nanofluid increases as the Pr increases. This is because the nanofluid with higher Prandtl number has a relatively low thermal conductivity, which reduces conduction, and thereby reduces the thermal boundary-layer thickness, and as a consequence, increases the heat transfer rate at the surface. For the case of the fluid velocity that decreases with the increase of \(Pr\), the reason is that fluid of the higher Prandtl number means more viscous fluid, which increases the boundary-layer thickness and thus, reduces the shear stress and consequently, retards the flow of the nanofluid. Also, it can be seen that the velocity distribution for small value of Prandtl number consist of two distinct regions. A thin region near the wall of the plate where there are large velocity gradients due to viscous effects and a region where the velocity gradients are small compared with those near the wall. In the later region, the viscous effects are negligible and the flow of fluid in the region can be considered to be inviscid. Also, such region tends to create uniform accelerated flow at the surface of the plate.Figure 12. Effects of Prandtl number on the velocity profile
Figure 13. Effects of Prandtl number on temperature profile
5.5. Effect of Schmidt and Grashof numbers on fluid velocity and temperature distributions
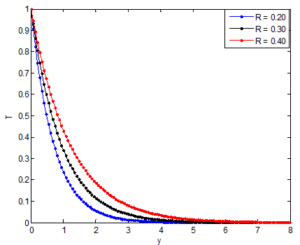
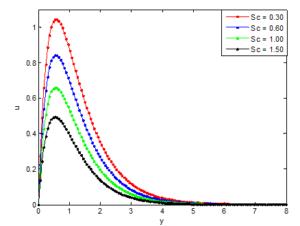
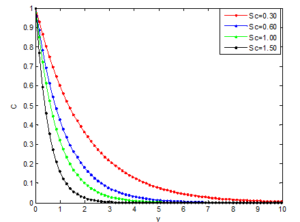
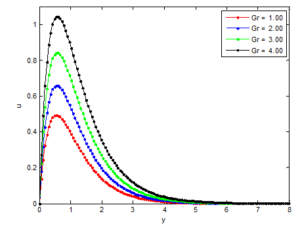
Figures 14 and 15 shows the effects of Schmidt number (Sc) on the velocity and concentration profiles of the Casson nanofluid, respectively. Figure 16 shows that the as Grashof number increases, the velocity of the fluid increases. However, as in the case of the effect of Prandtl number on the velocity and temperature distribution, it is depicted in the figures that the velocity of the nanofluid decreases as the Sc increases but the temperature of the nanofluid increases as the Sc increases. This is because the nanofluid with higher Schmidt number has a relatively low diffusion coefficient, which reduces mass diffusion thereby reduces the concentration boundary-layer thickness, and as a consequence, increases the mass transfer rate at the surface. In Figure 14, where the fluid velocity decreases with the increase of Sc, this is because the fluid of the higher Schmidt number means more viscous fluid, which increases the boundary-layer thickness and thus, reduces the shear stress and consequently, retards the flow of the nanofluid. It is also observed that the species concentration decreases with increasing Schmidt number as shown in Figure 15. It was also found that the temperature increases with increasing Schmidt number. A further investigation revealed that an increase in the Schmidt number leads to a decrease in Grashof number \(Gr\).Figure 14. Effects of Schmidt number on the velocity distribution
Figure 15. Effects of Schmidt number on the concentration distribution
Figure 16. Effects of Grashof number on the velocity distribution
5.6. Effects of magnetic field and flow medium Porosity on Casson nanofluid velocity distributions
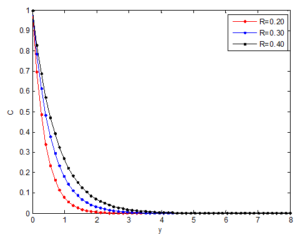
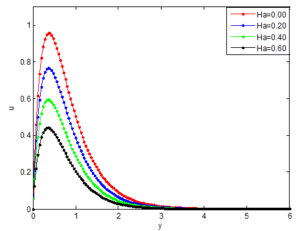
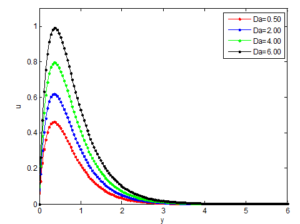
Figure 17 shows the effect of magnetic field on the flow velocity of the fluid. It is revealed that there is a diminution in the velocity field occurs for increasing value of the magnetic field number, Hartmann number (Ha). This confirms the general physical behavior of the magnetic field that say that the fluid velocity depreciates for improved values of Ha. The magnetic field produces Lorentz force which is drag-like force that produces more resistance to the flow and reduces the fluid velocity. So large Ha values implies that the Lorentz force increases and the resistance to the flow increases, and consequently, the velocity of the fluid decreases. Practically, the Lorentz force has a resistive nature which opposes motion of the fluid and as a result heat is produced which increases thermal boundary layer thickness and fluid temperature. The magnetic field tends to make the boundary layer thinner, thereby increasing the wall friction. Consequently, the boundary layer thickness is a decreasing function of Ha. i.e. presence of magnetic field slows fluid motion at boundary layer and hence retards the velocity field.A porous medium studies is very important in a number of engineering applications such as geophysics, die filling, metal processing, agricultural and industrial water distribution, oil recovery techniques, and injection molding. Therefore, Figure 18 shows the effect of flow medium porosity on the fluid velocity. As it is illustrated, the fluid velocity increases as the flow medium porosity, Darcy number increases. This is because, as the Darcy number increases, there is less resistance to fluid flow through the flow medium.
Figure 17. Effects of Hartmann number on the velocity distribution
Figure 18. Effects of Darcy number on the concentration distribution
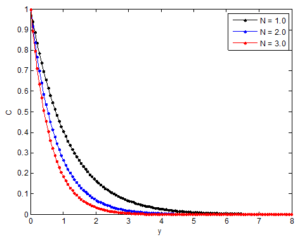
5.7. Effect of Buoyancy ratio parameter on the fluid velocity, temperature and concentration distributions
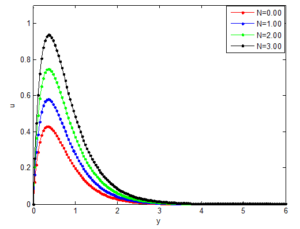
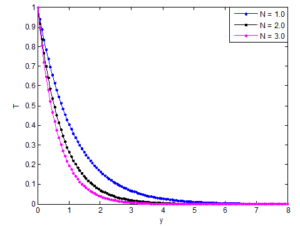
Figures 19, 20 and 21 show the impacts of buoyancy ratio parameter (N) on the velocity, temperature and concentration profiles. Figure 19 depicts that the as buoyancy ratio parameter increases, the velocity of the fluid increases. However, an increase in buoyancy ratio parameter leads to a decrease in the fluid temperature and concentration as shown in Figures 20 and 21.Figure 19. Effects of buoyancy ratio on the velocity distribution
Figure 20. Effects of buoyancy ratio on the temperature distribution
Figure 21. Effects of buoyancy ratio on the concentration distribution
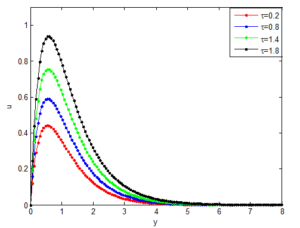
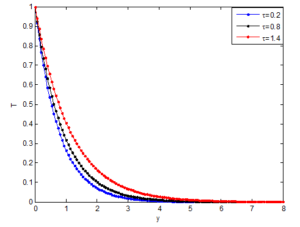
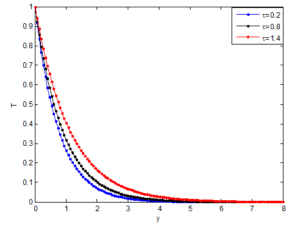
5.8. Effect of flow time on the fluid velocity, temperature and concentration distributions
Figure 22. Effects of flow time on the velocity distribution
Figure 23. Effects of flow on the temperature distribution
Figure 24. Effects of flow time on the concentration distribution
In order to shown the effects of flow time on the velocity, temperature and concentration distributions, Figures 19, 20 and 21 are presented Apart from the fact that the velocity, temperature and concentration distributions increase as the flow time increases, the results also shown the effects of the controlling parameters on the time to reach steady state velocity, temperature and concentration. In our further investigations, the required time to reach the steady state concentration, the transient velocity, Nusselt number and the local skin-friction decrease as the buoyancy ratio parameter and Schmidt number increase. Also, the steady-state temperature and velocity decrease as the buoyancy ratio parameter and Schmidt number increase
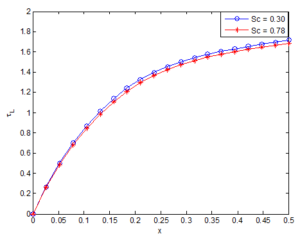
Figure 25. Effects of Schmidt number on local skin friction
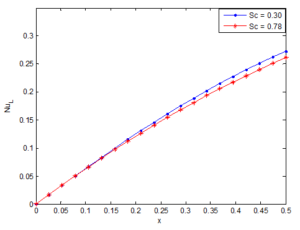
Figure 26. Effects of Schmidt number on Nusselt number
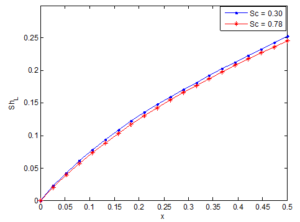
The effects of Schmidt number on local skin friction, Nusselt and Sherwood numbers are shown in Figures 25, 26 and 27, respectively. The figures reveal that the local skin friction, Nusselt and Sherwood numbers decrease as the Schmidt number increases. An opposite trend was recorded when the impact of the buoyancy ratio parameter on Nusselt number was investigated. In the investigation, it was found that as the local Nusselt number increases as the buoyancy ratio parameter increases. It was shown that at small values of x (near the leading edge of the plate), the local Nusselt number is not affected by both buoyancy ratio parameter and Schmidt number due to the pure diffusion and conduction at the location
Figure 27. Effects of Schmidt number on Sherwood number
6. Conclusion
In this present study, the transient free convection heat and mass transfer of Casson nanofluid past an isothermal vertical flat plate embedded in a porous media under the influences of thermal radiation and magnetic field have been investigated. The governing systems of nonlinear partial differential equations of the flow, heat and mass transfer processes are solved using implicit finite difference scheme of Crank-Nicolson type. The numerical solutions are used to carry out parametric studies and the follow results were established:- 1. The temperature and the concentration of the fluid increase as the Casson fluid and radiation parameters as well as Prandtl and Schmidt numbers increase.
- 2. The increase in the Grashof number, radiation, buoyancy ratio and flow medium porosity parameters causes the velocity of the fluid to increase. However, the Casson fluid parameter, buoyancy ratio parameter, the Hartmann (magnetic field parameter), Schmidt and Prandtl numbers decrease as the velocity of the flow increases.
- 3. The time to reach the steady state concentration, the transient velocity, Nusselt number and the local skin-friction decrease as the buoyancy ratio parameter and Schmidt number increase.
- 4. The steady-state temperature and velocity decrease as the buoyancy ratio parameter and Schmidt number increase.
- 5. The local skin friction, Nusselt and Sherwood numbers decrease as the Schmidt number increases. However, the local Nusselt number increases as the buoyancy ratio parameter increases.
Nomenclature
\(\mathbf{B_{o}}\) electromagnetic induction
\(\mathbf{c_{p}}\) specific heat capacity
\(\mathbf{C}\) species concentration
\(\mathbf{D}\) species diffusion coefficient
\(\mathbf{g}\) acceleration due to gravity
\(\mathbf{Gr}\) Grashof number
\(\mathbf{Ha}\) Hartmann number/magnetic field parameter
\(\mathbf{k}\) thermal conductivity
\(\mathbf{K}\) the absorption coefficient
\(\mathbf{m}\) shape factor
\(\mathbf{N}\) buoyancy ratio parameter
\(\mathbf{p}\) pressure
\(\mathbf{Pr}\) Prandtl number
\(\mathbf{\overline{p}}\) pressure
\(\mathbf{R}\) Radiation number
\(\mathbf{Sc}\) Schmidt number
\(\mathbf{t}\) time
\(\mathbf{\overline{T}}\) temperature of the fluid
\(\mathbf{\overline{u}}\) velocity component in x-direction
\(\mathbf{\overline{v}}\) velocity component in y-direction
\(\mathbf{U_{w}}\) fluid inflow velocity at the wall
\(\mathbf{\overline{x}}\) coordinate axis parallel to the plate
\(\mathbf{\overline{y}}\) coordinate axis perpendicular to the plate.
Symbols
\(\beta\) volumetric extension coefficients
\(\rho_{nf}\) density of the nanofluid
\(\rho_{f}\) density of the base fluid
\(\mu_{nf}\) dynamic viscosity of the nanofluid
\(\rho_{s}\) density of the solid/nanoparticles
\(\phi\) fraction of nanoparticles in the nanofluid
\(\gamma\) Casson parameter
\(\tau\) shear stress
\(\tau_{o}\) Casson yield stress,
\(\mu\) dynamic viscosity
\(\sigma\) shear rate
Subscript
\(\mathbf{f}\) fluid
\(\mathbf{s}\) solid
\(\mathbf{nf}\) nanofluid
\(\mathbf{w}\) wall.
Acknowledgments
The author expresses sincere appreciation to University of Lagos, Nigeria for providing material supports and good environment for this work.Conflict of Interests
''The author declares no conflict of interest.''References
- Schmidt, E., & Beckmann, W. (1930). The temperature and velocity field in front of a vertical plate that emits heat with natural convection. Engineering Mechanics and Thermodynamics , 1 (11), 391-406. [Google Scholor]
- Ostrach, S. (1952). An analysis of laminar free-convection flow and heat transfer about a flat plate parallel to the direction of the generating body force (No. NACA-TN-2635). National Aeronautics and Space Administration Cleveland Oh Lewis Research Center. [Google Scholor]
- Sparrow, E. M., & Gregg, J. L. (1958). Similar solutions for free convection from a nonisothermal vertical plate. Trans. ASME, 80(2), 379-386. [Google Scholor]
- Cianfrini, C., Corcione, M., & Fontana, D. M. (2002). Laminar free convection from a vertical plate with uniform surface heat flux in chemically reacting systems. International Journal of Heat and Mass Transfer, 45(2), 319-329. [Google Scholor]
- LeFevre, E. J. (1956). Laminar free convection from a vertical plane surface. NEL. [Google Scholor]
- Stewartson, K., & Jones, L. T. (1957). The heated vertical plate at high Prandtl number. Journal of the Aeronautical Sciences, 24(5), 379-380. [Google Scholor]
- Eshghy, S. (1971). Free-convection layers at large Prandtl number. Zeitschrift für angewandte Mathematik und Physik ZAMP, 22(2), 275-292. [Google Scholor]
- Roy, S. (1973). High-Prandtl-number free convection for uniform surface heat flux. 124-126.[Google Scholor]
- Kuiken, H. K. (1968). An asymptotic solution for large Prandtl number free convection. Journal of Engineering Mathematics, 2(4), 355-371. [Google Scholor]
- Kuiken, H. K. (1969). Free convection at low Prandtl numbers. Journal of Fluid Mechanics, 37(4), 785-798. [Google Scholor]
- Kuiken, H. K., & Rotem, Z. (1971). Asymptotic solution for plume at very large and small Prandtl numbers. Journal of Fluid Mechanics, 45(3), 585-600. [Google Scholor]
- Na, T. Y., & Habib, I. S. (1974). Solution of the natural convection problem by parameter differentiation. [Google Scholor]
- Merkin, J. H. (1985). A note on the similarity solutions for free convection on a vertical plate. Journal of Engineering Mathematics, 19(3), 189-201. [Google Scholor]
- Merkin, J. H., & Pop, I. (1996). Conjugate free convection on a vertical surface. International Journal of heat and Mass transfer, 39(7), 1527-1534.[Google Scholor]
- Ali, F. M., Nazar, R., & Arifin, N. M. (2009). Numerical investigation of free convective boundary layer in a viscous fluid. The American Journal of Scientific Research, 5, 13-19. [Google Scholor]
- Motsa, S. S., Shateyi, S., & Makukula, Z. (2011). Homotopy analysis of free convection boundary layer flow with heat and mass transfer. Chemical Engineering Communications, 198(6), 783-795. [Google Scholor]
- Motsa, S. S., Makukula, Z. G., & Shateyi, S. (2013). Spectral local linearisation approach for natural convection boundary layer flow. Mathematical Problems in Engineering, 2013.[Google Scholor]
- Ghotbi, A. R., Bararnia, H., Domairry, G., & Barari, A. (2009). Investigation of a powerful analytical method into natural convection boundary layer flow. Communications in Nonlinear Science and Numerical Simulation, 14(5), 2222-2228.[Google Scholor]
- Mosayebidorcheh, S., & Mosayebidorcheh, T. (2012). Series solution of convective radiative conduction equation of the nonlinear fin with temperature dependent thermal conductivity. International Journal of Heat and Mass Transfer, 55(23-24), 6589-6594. [Google Scholor]
- Sheikholeslami, M. (2016). CVFEM for magnetic nanofluid convective heat transfer in a porous curved enclosure. The European Physical Journal Plus, 131(11), 413. [Google Scholor]
- Sheikholeslami, M., & Ganji, D. D. (2015). Hydrothermal analysis in engineering using control volume finite element method. Academic Press.[Google Scholor]
- Sheikholeslami, M. (2018). Application of control volume based finite element method (CVFEM) for nanofluid flow and heat transfer. Elsevier. [Google Scholor]
- Sheikholeslami, M., Rana, P., & Soleimani, S. (2017). Numerical study of MHD natural convection liquid metal flow and heat transfer in a wavy enclosure using CVFEM. Heat Transfer Research, 48(2), 121-138. [Google Scholor]
- Mosayebidorcheh, S., Rahimi-Gorji, M., Ganji, D. D., Moayebidorcheh, T., Pourmehran, O., & Biglarian, M. (2017). Transient thermal behavior of radial fins of rectangular, triangular and hyperbolic profiles with temperature-dependent properties using DTM-FDM. Journal of Central South University, 24(3), 675-682. [Google Scholor]
- Attia, H. A. (2006). Unsteady MHD Couette flow and heat transfer of dusty fluid with variable physical properties. Applied Mathematics and Computation, 177(1), 308-318. [Google Scholor]
- Mosayebidorcheh, S., Mosayebidorcheh, T., & Rashidi, M. M. (2014). Analytical solution of the steady state condensation film on the inclined rotating disk by a new hybrid method. Scientific Research and Essays, 9(12), 557-565. [Google Scholor]
- Mosayebidorcheh, S., Vatani, M., Ganji, D. D., & Mosayebidorcheh, T. (2014). Investigation of the viscoelastic flow and species diffusion in a porous channel with high permeability. Alexandria Engineering Journal, 53(4), 779-785. [Google Scholor]
- Akter, M. S., Islam, M. R., Mollah, M. T., & Alam, M. M. (2019, July). Hall effects on Casson fluid flow along a vertical plate. In AIP Conference Proceedings (Vol. 2121, No. 1, p. 040004). AIP Publishing LLC.[Google Scholor]
- Dash, R. K., Mehta, K. N., & Jayaraman, G. (1996). Casson fluid flow in a pipe filled with a homogeneous porous medium. International Journal of Engineering Science, 34(10), 1145-1156. [Google Scholor]
- Eldabe, N. T. M., Saddeck, G., & El-Sayed, A. F. (2001). Heat transfer of MHD non-Newtonian Casson fluid flow between two rotating cylinders. Mechanics and Mechanical Engineering, 5(2), 237-251. [Google Scholor]
- Nadeem, S., Haq, R. U., Akbar, N. S., & Khan, Z. H. (2013). MHD three-dimensional Casson fluid flow past a porous linearly stretching sheet. Alexandria Engineering Journal, 52(4), 577-582.[Google Scholor]
- Raptis, A., & Perdikis, C. (1998). Viscoelastic flow by the presence of radiation. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik: Applied Mathematics and Mechanics, 78(4), 277-279. [Google Scholor]
- Seddeek, M. A. (2002). Effects of radiation and variable viscosity on a MHD free convection flow past a semi-infinite flat plate with an aligned magnetic field in the case of unsteady flow. International Journal of Heat and Mass Transfer, 45(4), 931-935. [Google Scholor]
- Mabood, F., Imtiaz, M., Alsaedi, A., & Hayat, T. (2016). Unsteady convective boundary layer flow of Maxwell fluid with nonlinear thermal radiation: a numerical study. International Journal of Nonlinear Sciences and Numerical Simulation, 17(5), 221-229. [Google Scholor]
- Hayat, T., Muhammad, T., Alsaedi, A., & Alhuthali, M. S. (2015). Magnetohydrodynamic three-dimensional flow of viscoelastic nanofluid in the presence of nonlinear thermal radiation. Journal of Magnetism and Magnetic Materials, 385, 222-229. [Google Scholor]
- Farooq, M., Khan, M. I., Waqas, M., Hayat, T., Alsaedi, A., & Khan, M. I. (2016). MHD stagnation point flow of viscoelastic nanofluid with non-linear radiation effects. Journal of molecular liquids, 221, 1097-1103. [Google Scholor]
- Shehzad, S. A., Abdullah, Z., Alsaedi, A., Abbasi, F. M., & Hayat, T. (2016). Thermally radiative three-dimensional flow of Jeffrey nanofluid with internal heat generation and magnetic field. Journal of Magnetism and Magnetic Materials, 397, 108-114. [Google Scholor]
- Sheikholeslami, M., & Bhatti, M. M. (2017). Forced convection of nanofluid in presence of constant magnetic field considering shape effects of nanoparticles. International Journal of Heat and Mass Transfer, 111, 1039-1049. [Google Scholor]
- Haq, R. U., Nadeem, S., Khan, Z. H., & Noor, N. F. M. (2015). Convective heat transfer in MHD slip flow over a stretching surface in the presence of carbon nanotubes. Physica B: Condensed Matter, 457, 40-47.[Google Scholor]
- Talley, L. D. (2011). Descriptive physical oceanography: an introduction. Academic press. [Google Scholor]
- Pastoriza-Gallego, M. J., Lugo, L., Legido, J. L., & Piñeiro, M. M. (2011). Thermal conductivity and viscosity measurements of ethylene glycol-based Al 2 O 3 nanofluids. Nanoscale research letters, 6(221), 1-11. [Google Scholor]
- Aberoumand, S., & Jafarimoghaddam, A. (2017). Experimental study on synthesis, stability, thermal conductivity and viscosity of Cu–engine oil nanofluid. Journal of the Taiwan Institute of Chemical Engineers, 71, 315-322. [Google Scholor]
- Han, H., Jin, J., & Wu, X. (2005). A finite-difference method for the one-dimensional time-dependent Schrödinger equation on unbounded domain. Computers & Mathematics with Applications, 50(8-9), 1345-1362.[Google Scholor]
- Carnahan, B., Luther, H. A., & Wilkes, J. O. (1969). Applied Numerical Methods. John Willey & Sons. Inc., New York. [Google Scholor]