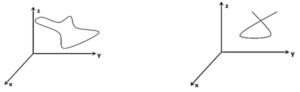Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2022.0084
Line integral and its applications
Aschale Moges Belay
Department of Mathematics, Debark University, P.O.Box 90, Ethiopia.; etenesh.rem@gmail.com
Abstract
Keywords:
1. Introduction
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve. The terms path integral, curve integral, and curvilinear integral are also used; contour integral as well, although that is typically reserved for line integral in the complex plane [1].
The function to be integrated may be a scalar field or a vector field. The value of the line integral is the sum of values of the field at all points on the curve, weighted by some scalar function on the curve (commonly arc length) or, for a vector field, the scalar product of the vector field with a differential vector in the curve. This weighting distinguishes the line integral from simpler integrals defined on intervals. Many simple formula in physics (for example, \(W = F \cdot s\)) have natural continuous analogs in terms of line integrals ( \(W = \int_{c}F~\cdot~ ds\)). The line integral finds the work done on an object moving through an electric or gravitational field, for example [1].
The main purposes of this study are to
- show the areas where line integral is applicable;
- point out the role of line integral in solving practical problems.
2. Preliminaries
2.1. Space curves
Since the concept of vector valued function is useful to define space curve, let us define vector valued function before we define space curve.Definition 1.(Vector valued function [2]) A function \(r : t\longrightarrow\mathbf{V}\) is said to be a vector valued function if \(t \in ~\mathbb{R}\) and \(\mathbf{V}\) is \(n-\)dimensional vector.
Example 1. \(r(t) = 2ti-t^{2}j\) and \(r(t) = i-tj + (\sin t)k\) for any real number \(t\) are vector valued functions.
Definition 2.(Space curve [2]) A space curve (or simply curve) is the range of a continuous vector valued function on an interval of real numbers.
We will generally use \(C\) to denote a curve and \(r\) to denote a vector valued function whose range is a curve \(C.\) In that case we say that \(C\) is parameterized by \(r\) or that \(r\) is a parametrization of \(C.\)There are so many types of curves. Some of them are listed as follows;
Definition 3.(Simple curve [3]) A curve \(C\) is said to be simple if it has no self-intersection except possibly at the end points of the interval of a parameter \(t.\)
Figure 1. (a) is a simple curve, whereas (b) is a non-simple curve.
Definition 4.(Closed curve [3]) A curve \(C\) is said to be closed if it has a parametrization \(r(t)\) on the closed interval \([a, b]\) such that \(r(a) = r(b).\) In other words, a curve \(C\) is said to be closed if its initial and terminal points coincides.
Example 2.
- A curve \(C\) parameterized by \(r(t) = (\cos t )i + (\sin t )j\) for \(0\leq t\leq 2\pi\) is a closed curve since \(r(0) = r(2\pi) = i.\)
- A curve \(C\) parameterized by \(r(t) = ti + t^{2}j-k\) for \(0\leq t\leq 1\) is not a closed curve since \(r(0) \neq r(1).\)
Definition 5.(Simple closed curve [3]) A curve \(C\) is said to be simple closed if it is both simple and closed curve.
Definition 6.(Smooth curve [3]) A vector valued function \(r(t)\) is said to be smooth on an interval \(I\) if \(r'(t)\) is continuous on \(I\) and \(r'(t) \neq 0\) for each interior point of \(I.\) A curve \(C\) is said to be smooth if its parametrization \(r(t)\) is smooth.
Example 3.
- Consider a curve \(C\) parameterized by \begin{equation*} r(t) = t^{2}i + 2tj + t^{3}k. \end{equation*} The derivative of \(r(t)\) with respect to \(t\) is \begin{equation*} r'(t) = 2ti + 2j + 3t^{2}k. \end{equation*} Since \(r'(t)\) is continuous and \(r'(t) \neq 0\) for any \(t,\) then \(r(t)\) is smooth on \((-\infty,~\infty)\). Because of this, a curve \(C\) is smooth on \((-\infty,~\infty)\).
- Consider a curve C\('\) parameterized by \begin{equation*}r(t)=(t-sint)i + (1-cost)j, \ \ \ -2\pi \leq t \leq 2\pi \end{equation*} The derivative of \(r(t)\) with respect to \(t\) is \begin{equation*}r'(t) = (1-\cos t)i + (\sin t)j.\end{equation*} Even though \(r'(t)\) is continuous on \([-2\pi,~2\pi],\) \(r(t)\) is not smooth on \([-2\pi,~2\pi]\) because \(r'(t) = 0\) at \(t = 0.\) Because of this, a curve \(C'\) is not smooth on \([-2\pi,~2\pi].\)
Definition 7.(Piecewise smooth curve [3]) A vector valued function \(r(t)\) is said to be piecewise smooth on an interval \(I\) if \(I\) is expressible as the union of finite number of subintervals such that \(r(t)\) is smooth on each of the subintervals and the one-sided derivatives of \(r(t)\) exist at each interior point of \(I.\) A curve \(C\) is said to be piecewise smooth if its parametrization \(r(t)\) is a piecewise smooth.
For 2 in Example 3, \(r(t)\) is piecewise smooth because \(r(t)\) is smooth on subintervals \([-2\pi, 0]\) and \([0, 2\pi]\), and one-sided derivatives of \(r(t)\) exist on \((-2\pi,~2\pi).\) Because of this, that curve is a piecewise smooth on \([-2\pi,~2\pi].\)
Remark 1. Any smooth curve can be piecewise smooth but the converse is not always true.
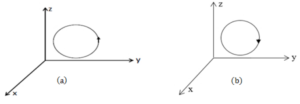
Definition 8.(Counter clockwise oriented curve [4]) A curve \(C\) is said to be counter clockwise oriented if it is always lying to the left of the path while moving along \(C.\)
Definition 9. (Clockwise oriented curve [4]) A curve \(C\) is said to be clockwise oriented if it is always lying to the right of the path while moving along \(C.\)
Figure 2. (a) is counter clockwise oriented curve whereas (b) is clockwise oriented curve
Definition 10. (Positively and Negatively oriented curves [4])
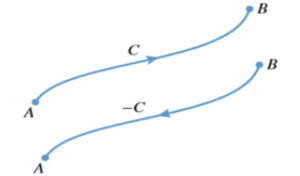
- A curve \(C\) is said to be positively oriented if the values of parameter \(t\) is increasing while moving along \(C.\)
- A curve \(C\) is said to be negatively oriented if the values of parameter \(t\) is decreasing while moving along \(C.\)
Figure 3. Curve \(C\) and \(- C\) are positively and negatively oriented curves respectively.
Remark 2. If the curve is simple closed, then it is
- positively orientation corresponds to counter clockwise orientation,
- negatively orientation corresponds to clockwise orientation.
It is possible to express different curves using a parameter. Now, let us see smooth parametrization of important curves which we will use frequently.
Line segment: Suppose \(L\) is a line segment from point \(A(x_{0},~y_{0},~z_{0})\) to another point \(B(x_{1},~y_{1},~z_{1})\). Then the parametric equation of this line segment is
\[ \begin{cases} x=x_{0} + (x_{1}- x_{0})t \\ y=y_{0}+(y_{1}-y_{0})t\\ z=z_{0}+(z_{1}-z_{0})t \end{cases}\] for \(0\leq t\leq 1.\) Therefore, the smooth parametrization of this line segment is \[[x_{0}+(x_{1}-x_{0})t]i +[y_{0}+(y_{1}-y_{0} )t]j+[z_{0}+(z_{1}-z_{0})t]k\;\;\;\;\;\;\; \text{for }\;\;\;\;\;\;0\leq t\leq 1.\]Circle: Suppose \(C\) is a circle with equation \((x-h)^{2}+(y-k)^{2}=r^{2}\). Then the parametric equation of this circle is
\[ \begin{cases} x=h+r\cos t \\ y=k+r\sin t \end{cases}\] for \(0\leq t\leq 2\pi. \) Therefore, the smooth parametrization of this circle is \[[h+rcost]i+[k+r\sin t]j\;\;\;\;\;\;\; \text{for }\;\;\;\;\;\;0\leq t\leq 2\pi.\]Ellipse: Suppose \(E\) is an ellipse with equation \(\frac{(x-h)^{2}}{a^{2}} +\frac{(y-k)^{2}}{b^{2}} =1\). Then the parametric equation of this ellipse is
\[\begin{cases} x=h+a\cos t \\ y=k+b\sin t \end{cases}\] for \(0\leq t\leq 2\pi. \) Therefore, the smooth parametrization of this ellipse is \[[h+acost]i+[k+b\sin t]j\;\;\;\;\;\;\; \text{for }\;\;\;\;\;\;0\leq t\leq 2\pi.\]Graph of a function: Suppose \(C\) is a graph of a function \(y = g(x)\) for \(a\leq x \leq b\). Then the parametric equation of this graph is
\[\begin{cases} x=t\\ y=g(t) \end{cases} \] for \(a\leq t\leq b. \) Therefore, the smooth parametrization of this graph is \[ti+g(t)j \;\;\;\;\;\;\; \text{for }\;\;\;\;\;\;a\leq t\leq b.\]Region formed by a plane \(z = m\) and a circle \((x-h)^{2}+(y-k)^{2}=r^{2}\): The smooth parametrization of this region is
\[[h+r\cos t]i+[ k+r\sin t]j+mk\;\;\;\;\;\;\; \text{for }\;\;\;\;\;\;0\leq t \leq 2\pi.\]Sphere: Suppose \(S\) is a sphere with equation \((x-h)^{2} + (y-k)^{2} + (z-w)^{2} =\rho^{2}\). Then the parametric equation of this sphere is
\[ \begin{cases} x=h+\rho \cos\beta \sin\theta \\ y=k+\rho \sin\beta \sin\theta\\ z=w+\rho \cos\theta \end{cases} \] for \(\beta \in [0,~ 2\pi]~and~\theta \in [0,~ \pi] \). Therefore, the smooth parametrization of this sphere is \[[h+\rho \cos\beta \sin\theta]i+[k+\rho \sin\beta \sin\theta]j +[w+\rho \cos\theta] k\;\;\;\;\;\;\; \text{for }\;\;\;\;\;\;\beta \in [0,~ 2\pi]~and~\theta \in [0,~ \pi].\]Definition 11. (Length of a curve [2]) Let \(C\) be a curve with a piecewise smooth parametrization \(r(t)\) defined on \([a, b],\) then the length \(L\) of \(C\) is \begin{equation*} L=\int_{a}^{b}|r'(t)|dt=\int_{a}^{b}|\frac{dr}{dt}|dt. \end{equation*}
Remark 3.If \(r(t) = x(t)i + y(t)j + z(t)k,\) then \begin{equation*} L=\int_{a}^{b}\sqrt{[x'(t)]^{2}+[y'(t)]^{2}+[z'(t)]^{2} }dt. \end{equation*}
Example 4. Consider a curve parameterized by \(r(t) = (\cos t)i + (\sin t)j + tk\) for \(0\leq t \leq 2\pi\). The derivative of \(r(t)\) with respect to \(t\) is \begin{equation*} r'(t)=(-\sin t)i+(\cos t )j+k. \end{equation*} The length of this curve on \([0, 2\pi]\) is \begin{equation*} L=\int_{0}^{2\pi}\sqrt{(-\sin t)^{2}+(\cos t)^{2}+1^{2}} dt =\int_{0}^{2\pi}\sqrt{2}dt=2\sqrt{2}\pi. \end{equation*}
2.2. The concepts of scalar and vector fields
Definition 12. (Scalar field [3]) A function \(f : P\rightarrow Q\) is said to be a scalar field if \(P\in\mathbb{R}^{n}\) and \(Q\in\mathbb{R}\).
Example 5. \(f(x, y, z) = xyz\) is a scalar field.
Definition 13. (Vector field [3]) A function\( F : P\rightarrow\mathbf{V}\) is said to be a vector field if \(P\in\mathbb{R}^{n}\) and \(\mathbf{V}\) is \(n-\)dimensional vector.
Example 6. \(F(x, y, z) = x^{2} i+y^{2} j+z^{2} k\) is a vector field.
Remark 4.A vector field \(F\) formed by the gradient of a scalar function \(f\) is said to be gradient vector field and denoted by \begin{equation*} F = \triangledown f=(\frac{\partial}{\partial x}i + \frac{\partial}{\partial y}j + \frac{\partial }{\partial z}k)f=f_{x}i+f_{y}j+f_{z}k. \end{equation*}
Definition 14. (Conservative vector field [3]) A vector field \(F\) is said to be conservative if there exists a differentiable function \(f\) such that \(F = \triangledown f.\) The function \(f\) is called potential function for \(F.\)
Example 7. A function \(F(x, y, z) = 3x^{2} i+3y^{2} j+3z^{2}k\) is conservative because there exists a potential function \(f(x, y, z) = x^{3} +y^{3}+z^{3}\) for \(F\) such that \(F = \triangledown f.\)
Before we see test of conservativeness, let us define the curl of a vector field \(F.\)Definition 15. (Curl of a vector field [3]) Let \(F = Mi + Nj + Pk\) be a vector field such that all the partial derivatives of \(M, N\) and \(P\) exist, then the curl of \(F,\) denoted by curl \(F,\) is given by \[\text{curl}~F=\triangledown \times F = \begin{vmatrix} i & j & k \\ \frac{\partial}{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ M & N & P \end{vmatrix} .\]
Remark 5. If \(F = Mi +Nj,\) then \(\text{curl} F = (N_{x}-M_{y})k\).
Example 8. Consider a vector field \(F(x, y, z) = 3x^{2}i + xyj - y^{2}zk\). Then the curl of \(F\) is given by \[ \begin{vmatrix} i & j & k \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ 3x^{2} & xy & -y^{2} z \end{vmatrix} = -2yzi + yk.\]
Now let us see test of conservativeness and procedures of finding potential function of conservative vector field.Test of conservativeness [3]
The concept of curl of a vector field \(F\) is useful to test \(F\) is conservative or not i.e., \(F\) is conservative if curl \(F = 0.\) A vector field in Example 8 is not conservative since \(\text{curl} F\) is not always \(0.\)Procedures of finding potential function of conservative vector field
We are able to find a potential function for a given conservative vector field \(F.\) The procedures of finding a potential function \(f\) for a given conservative vector field \(F(x, y, z) = Mi + Nj + Pk\) are listed as follows;Step-1 ( Variable separation) In this step, we express the function \(f\) as a sum of three functions in the form of \[f(x,~y,~z)=k(x,~y,~z)+g(y,~z)+h(z).\] So, \(f_{x}=k_{x},~f_{y}=k_{y}+g_{y}\) and \(f_{z}=k_{z}+g_{z}+h_z.\) Since \(F = \triangledown f,\) then \(f_{x}=k_{x}=M,~f_{y}=k_{y}+g_{y}=N\) and \(f_{z}=k_{z}+g_{z}+h_{z}=P\).
Step-2 Integrate \(f_{x}=k_{x}=M\) with respect to \(x.\) That is \(k(x, y, z)\) = \(\int Mdx\).
Step-3 Integrate \(f_{y}=k_{y}+g_{y}=N\) with respect to \(y.\) That is \(g(y,z)=\int(N-k_{y})dy\).
Step-4 Integrate \(f_{z}=k_{z}+g_{z}+h_{z}=P\) with respect to \(z.\) That is \(h(z)=\int(P-k_{z}-g_{z})dz\).
Step-5 Finally, we write \(f(x, y, z) = k(x, y, z) + g(y, z) + h(z)\) using the above results.
Example 9. Consider a vector field \(F(x, y, z)= xy^{2}z^{2} i+x^{2} y z^{2} j+x^{2} y^{2} zk\). Then \( M=x y^{2} z^{2},~ N=x^{2} y z^{2}\) and \(P=x^{2} y^{2} z\).
Firstly, let us test \(F\) is conservative or not. \[ \text{curl} F = \begin{vmatrix} i & j & k \\ \frac{\partial }{\partial x} & \frac{\partial }{\partial y} & \frac{\partial }{\partial z} \\ xy^{2}z^{2} & x^{2} y z^{2} &x^{2} y^{2} z \end{vmatrix} = 0.\] Hence, this vector field is conservative.- Step-1 Suppose \(f(x, y, z) = k(x, y, z) + g(y, z) + h(z).\)
- Step-2 \(k(x, y, z) = \int Mdx=\int x y{^2} z^{2} dx=\frac{1}{2} x^{2} y^{2} z^{2} + c_{1}.\)
- Step-3 \(g(y, z) = \int(N-k_{y} )dy = \int0dy = 0 + c_{2} = c_{2}.\)
- Step-4 \(h(z) = \int(P-k_{z}-g_{z} )dz=\int0dz=0 + c_{3} = c_{3}\).
- Step-5 The potential function for the given conservative vector field is \[f(x, y, z) = \frac{1}{2} x^{2} y^{2} z^{2}+c\] where \(c = c_{1} + c_{2} +c_{3}\).
3. Line integrals
Under this section, we will see detail description of line integral in Cartesian and Complex planes.3.1. Line integral in Cartesian plane
There are two types of line integral in Cartesian plane. These are line integral of scalar and vector fields.Definition 16.(Line integral of scalar field [3]) Let \(f\) be a continuous scalar field on a smooth curve \(C\) parameterized by \(r(t) = x(t)i + y(t)j + z(t)k\) on \([a, b],\) then the line integral of \(f\) on \(C\) is given by \begin{equation*} \int_{C} f(x,y,z)ds = \int_{a}^{b}f(x(t),~y(t),~z(t)) |r'(t)|dt. \end{equation*}
Example 10.
- Consider \(\int_{C} (x+y+ z)ds\) where \(C\) is the line segment from \((0, 1, 1)\) to \((2, 2, 3).\) The smooth parametrization of the line segment from \((0, 1, 1)\) to \((2, 2, 3)\) is \begin{equation*} r(t) = 2ti + (1 + t)j + (1 + 2t)k; \ \ \ 0\leq t \leq 1\,, \end{equation*} implies that \(| r' (t)|=3\) and \(x(t) + y(t) + z(t) = 2 + 5t.\) Hence, \begin{equation*} \int_{C} (x+y+ z)ds = \int_{0}^{1}3(2+5t) dt= \frac{27}{2}. \end{equation*}
- Consider \(\int_{C} (x+y)ds\) where \(C\) is the upper half of the circle \(x^{2}+y^{2}=25\) in counter clockwise orientation. The smooth parametrization of this half circle is \[r(t) = (5\cos t)i + (5\sin t)j;\;\;\;\;\;\;\;0 \leq t \leq \pi\,,\] implies \(| r' (t)|=5\) and \(x(t) + y(t) = 5\cos t + 5\sin t.\) Hence, \[\int_{C} (x+y)ds = \int_{0}^{\pi}5(5\cos t+5\sin t) dt=50.\]
Definition 17.(Line integral of vector field [3]) Let \(F = Mi + Nj + Pk\) be a continuous vector field defined on a smooth curve \(C\) parameterized by \(r(t) = x(t)i + y(t)j + z(t)k\) on \([a, b],\) then the line integral of \(F\) on \(C\) is given by \[ \int_{C} F\cdot dr=\int_{a}^{b} F(x(t),~y(t),~z(t)) \cdot r'(t)dt.\]
Example 11. Consider \(F(x, y) = 3yi + 3xj\) and \(C\) is the ellipse \(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) in the \(xy-\)plane. The smooth parametrization of this ellipse is \[r(t) = (3\cos t)i + (2\sin t)j; \;\;\;\;\;\;0\leq t \leq 2\pi\,,\] implies \[F(x(t),y(t))\cdot r'(t)=[(6\sin t)i +(9\cos t)j]\cdot [(-3\sin t)i +(2\cos t)j]=18\cos 2t.\] Hence, the line integral of \(F\) on \(C\) is \( \int_{C} F(x,y)\cdot dr=\int_{o}^{2\pi}(18 \cos 2t) dt=0\).
Remark 6. If \(a\) and \(b\) are constants, and \(F\) and \(G\) are continuous vector field on a smooth curve \(C\) parameterized by \(r(t),\) then the following properties hold;
- \(\int_{C} [aF\pm bG]\cdot dr=a\int_{C} F\cdot dr\pm b\int_{C} G\cdot dr\),
- \(\int_{-C} F\cdot dr=-\int_{C} F\cdot dr\),
- \(\int_{C} F\cdot dr=\int_{C_{1} } F\cdot dr+\int_{C_{2} } F\cdot dr +...+\int_{C_{n}} F\cdot dr ~ if ~C= \bigcup _{i=1}^{n} C_{i}\),
- if \(F\) is conservative and \(C\) is from \(P\) to \(Q,\) then \(\int_{C} F\cdot dr=f(Q)-f(P)\) where \(f\) is a potential function for \(F.\) In other words, the line integral \(\int_{C} F\cdot dr\) is independent of the path if \(F\) is conservative,
- if \(F = Mi + Nj + Pk,\) then \(\int_{C} [Mdx+Ndy+Pdz]=\int_{C} F\cdot dr\).
Example 12.
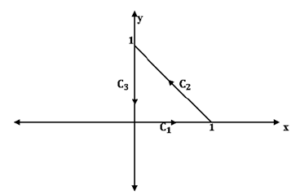
Consider \(F(x, y) = xi + yj \) and \( C\) is the triangle in a plane with vertices \(A(0, 0), B(1, 0)\) and \( C(0, 1)\) in counter clockwise orientation, see Figure 4.
Figure 4.
From Figure 4, \(C = C_{1} ~\bigcup ~C_{2} ~\bigcup~ C_{3}\), where \(C_{1}:x=t\) and \(y = 0; \;\;\;\;0\leq t \leq 1\), \(C_{2}:x=1-t\) and \(y = t;\;\;\;\;0\leq t \leq 1\), and \(C_{3}:x=o\) and \(y = 1\;\;t;\;\;\;\;0\leq t\leq 1\).
On \(C_{1},\) \[\int_{C_{1} } F\cdot dr=\int_{0}^{1}t dt=\frac{1}{2}.\] On \(C_{2},\) \[\int_{C_{2}} F\cdot dr=\int_{0}^{1}(2t-1) dt=0.\] On \(C_{3},\) \[\int_{C_{3 }} F\cdot dr=\int_{0}^{1}(t-1)dt=-\frac{1}{2}.\] Hence, \[\int_{C} F\cdot dr=\int_{C_{1 }} F\cdot dr+\int_{C_{2 }} F\cdot dr+ \int_{C_{3 }} F\cdot dr=\frac{1}{2}+0-\frac{1}{2}=0.\] In other way, since \(F\) is conservative, \( f(x, y) = \frac{x^{2}}{2}+\frac{y^{2}}{2}\) is a potential function for \(F\) and \( C\) is closed path, then \(\int_{C} F\cdot dr=f(0,0)-f(0,0)=0\).3.2. Line integral in complex plane
The line integral in complex plane is known as contour integral.Definition 18.(Contour integral [5]) If a function of complex variable \(f(z)\) is continuous on a smooth curve \(C\) parameterized by \(z(t) = x(t) + y(t)i\) on an interval \([a, b],\) then the contour integral of \(f\) on \(C\) is given by \[\int_{C} f(z)dz=\int_{a}^{b}f(z(t)) z'(t)dt.\]
Remark 7. Contour integral grants all properties of line integral in Cartesian plane.
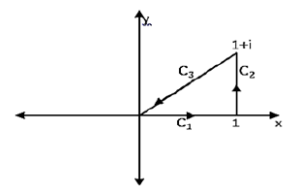
Example 13. Consider \(f(z) = z^{2}\) and \(C\) is given by Figure 5.
Figure 5.
From Figure 5, \(C = C_{1} ~\bigcup ~C_{2} ~\bigcup~ C_{3}\), wehere \(C_{1} : z(t) = t; \;\;\;0\leq t\leq 1\), \(C_{2}: z(t) = 1+ti; \;\;\;0\leq t\leq 1\) and \(C_{3}: z(t) = (1-t) + (1-t)i; \;\;\;0\leq t\leq 1\).
On \(C_{1},\) \[ \int_{C_{1 }} f(z)dz=\int_{0}^{1}t^{2} dt=\frac{1}{3}.\] On \(C_{2},\) \[\int_{C_{2 }} f(z)dz=\int_{0}^{1}(1+ti)^{2 }i dt=-1+\frac{2}{3} i.\] On \(C_{3},\) \[\int_{C_{3 }} f(z)dz=\int_{0}^{1}[(1-t)+(1-t)i]^{2} (-1-i)dt=\frac{2}{3}-\frac{2}{3} i.\] Hence, \[\int_{C} f(z)dz=\int_{C_{1 }} f(z)dz+\int_{C_{2}} f(z)dz+ \int_{C_{3}} f(z)dz=0.\]4. Applications of line integral
Line integral has physical and geometrical applications. Now, let us see selective applications of line integral in detail.4.1. Geometrical applications of line integral
In mathematics, line integral is used, in particular, for computations of- length of a curve,
- area of a region bounded by a closed curve
- volume of a solid formed by rotating a closed curve about the \(x-\) axis.
4.1.1. Length of a curve [6]
Let \(C\) be a piecewise smooth curve described by the position vector \(r(t);\alpha \leq t\leq \beta\), then the length of the curve is given by the line integral\begin{equation*} L=\int_{C} ds=\int_{\alpha}^{\beta}|\frac{dr}{dt}| dt = \int_{\alpha}^{\beta} \sqrt{(\frac{dx}{dt})^{2}+(\frac{dy}{dt})^{2}+(\frac{dz}{dt})^{2}} ~dt \end{equation*} where \(\frac{dr}{dt}\) is the derivative of \(r(t)\) with respect to \(t,\) and \( x(t), y(t), z(t)\) are the components of the position vector \(r(t).\)If the curve \(C\) is two-dimensional, the latter formula can be written in the form of
\begin{equation*} L=\int_{C} ds=\int_{\alpha}^{\beta}|\frac{dr}{dt}| dt = \int_{\alpha}^{\beta} \sqrt{(\frac{dx}{dt})^{2}+(\frac{dy}{dt})^{2}} ~dt. \end{equation*} If the curve \(C\) is the graph of a continuous and differentiable function \(y = f(x)\) on \([a, b]\) in the \(xy-\)plane, then the length of the curve is given by \begin{equation*} L=\int_{a}^{b}\sqrt{1+(\frac{dy}{dx})^{2}} ~dx. \end{equation*} Finally, if the curve \(C\) is given by the equation \(r = r(\theta ),\) \(\alpha \leq \theta \leq \beta\) in polar coordinates, and the function \(r(\theta)\) is continuous and differentiable in the interval \([\alpha, \beta],\) then the length of the curve is defined by the formula \begin{equation*} L=\int_{\alpha}^{\beta}\sqrt{(\frac{dr}{d\theta})^{2}+r^{2}}~ d\theta. \end{equation*}Example 14.
- Consider a space curve \(C\) parameterized by \(r(t) = (3t, 3t^{2}, 2t^{3})\) where \(0\leq t\leq 1\). The derivative of \(r(t)\) with respect to \(t\) is \(r'(t) = (3, 6t, 6t^{2})\). The length of this curve is \begin{equation*} L= \int_{C} ds= \int_{0}^{1} \sqrt{(3)^{2}+(6t)^{2}+(6t^{2} ){^2} } dt=\int_{0}^{1}(3+6t^{2} ) dt=5. \end{equation*}
- Consider a parabola \(y = x^{2}\) for \(0\leq x\leq 1\). The length of this curve is \begin{equation*} L=\int_{0}^{1} \sqrt{1+(2x)^2 } dx=\int_{0}^{1}\sqrt{1+4 x^{2}} dx ,\end{equation*} implies \begin{equation*} L=\frac{1}{2} \int_{0}^{arctan2} sec^{3} t dt=\frac{\sqrt{5}}{2}+\frac{1}{4} ln(\sqrt{5}+2)\approx 1.48. \end{equation*}
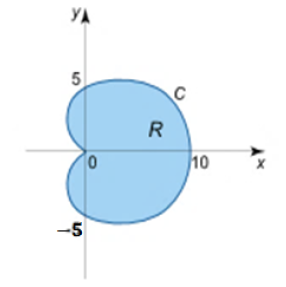
- Consider a cardioid given in polar coordinates by the equation \(r = 5(1 + \cos\theta)\), see Figure 6. The derivative of \(r(\theta)\) with respect to \(\theta\) is \(r' (\theta) = -5 \sin\theta\). The length of this cardioid is \begin{align*}L&= \int_{0}^ {2\pi}\sqrt{(-5 \sin\theta )^{2}+[5(1+\cos\theta)]^{2} } d\theta\\ &= 5\sqrt{2}\int_{0}^ {2\pi}\sqrt{1+\cos\theta} d\theta\\ &= 10\int_{0}^ {2\pi} \left|\cos(\frac{\theta}{2})\right| d\theta \\ &= 10\left[\int_{0}^ {\pi}\cos\left(\frac{\theta}{2}\right) d\theta - \int_{\pi}^ {2\pi}\cos\left(\frac{\theta}{2}\right) d\theta\right] \;\;\;\text{since}\;\;\; \left|\cos\left(\frac{\theta}{2}\right)\right| = \begin{cases} \cos\left(\frac{\theta}{2}\right) ~ \text{if}~ 0\leq \theta \leq \pi\\ -\cos\left(\frac{\theta}{2}\right) ~ \text{if} ~\pi \leq \theta \leq 2\pi \end{cases}\\ &= 40.\end{align*}
Figure 6.
4.1.2. Area of a region bounded by a closed Curve [6]
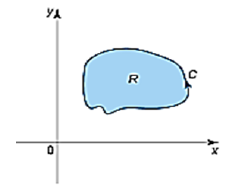
If \(C\) is a closed smooth piecewise curve in the \(xy-\)plane (Figure 7), then the area of the region \(R\) bounded by the curve is \(S=\oint_{C} xdy=-\oint_{C} ydx=\frac{1}{2} \oint_{C} [xdy-ydx].\)Figure 7.
Remark 8. It is supposed here that the contour \(C\) is traversed in the counterclockwise direction.
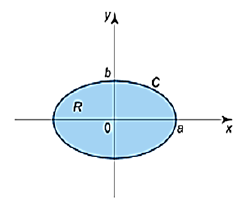
If the closed curve \(C\) is given in parametric form \(r(t) = (x(t), y(t))\) on \([\alpha,~ \beta],\) then the area of the corresponding region can be calculated by the formula \begin{equation*}S=\int_{\alpha}^{\beta}x(t) \frac{dy}{dt} dt=-\int_{\alpha}^{\beta}y(t) \frac{dx}{dt} dt=\frac{1}{2} \int_{\alpha}^{\beta}[x(t) \frac{dy}{dt}-y(t) \frac{dx}{dt}]dt \,. \end{equation*}Example 15. Consider a region bounded by the ellipse \(x = a\cos t, y = b\sin t; \;\;\;0\leq t \leq 2\pi\), see Figure 8.
Figure 8.
The area of this region is
\begin{equation*} S=\int_{0}^{2\pi}(a\cos t) (b\cos t)dt=ab\int_{0}^{2\pi}\cos^{2} tdt=\pi ab. \end{equation*}We can also get the following result using the other two formulas;
- \(S=-\int_{0}^{2\pi}(b\sin t)(-a\sin t )dt=ab\int_{0}^{2\pi}\sin^{2} tdt=\pi ab\),
- \(S=\frac{1}{2} \int_{0}^{2\pi}[(a\cos t) (b\cos t)-(b\sin t)(-a\sin t )]dt=\frac{1}{2} ab\int_{0}^{2\pi}dt=\pi ab\).
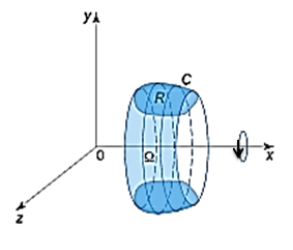
4.1.3 Volume of a solid formed by rotating a closed curve about the \(x-\)axis [6]
Let \(R\) be a region in the half-plane \(y\geq0\) bounded by a closed smooth piecewise curve \(C\) traversed in the counterclockwise direction. Suppose that the solid \(\Omega\) is formed by rotating the region \(R\) about the \(x-\)axis (Figure 9), then the volume of the solid is given by \begin{equation*} V=-\pi \oint_{C} y^{2}dx=-2\pi \oint_{C} xydy=-\frac{\pi}{2} \oint_{C} [2xydy+y^{2}dx]. \end{equation*}Figure 9.
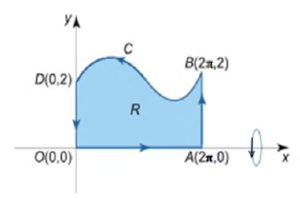
Example 16. Consider a solid formed by rotating the region \(R\) bounded by the curve \(y = 2-\sin x\) and the lines \(x = 0, x = 2\pi, y = 0\) about the \(x-\)axis (Figure 10).
Figure 10.
The volume of the solid is
\begin{align*} V&=-\pi \oint_{C} y^{2} dx=-\pi [\int_{OA} y^{2} dx+\int_{AB} y^{2} dx+\int_{BD} y^{2} dx+\int_{DO} y^{2} dx]\\ &=-\pi(0+0-9\pi+0)=9\pi^{2} \end{align*} where, since \(y = 0\) on \(OA\), so \(\int_{OA} y^{2} dx=\int_{0}^{2\pi}o^{2} dx=0\). Since, the smooth parametrization of \(AB\) is \(2\pi i +2tj\), so \[\int_{AB} y^{2} dx=\int_{2\pi}^{2\pi}y^{2}dx=\int_{0}^{1}(2t)^{2}\times 0~ dt =0.\] Since \(y = 2- \sin x\) on \(BD\), so \[\int_{BD} y^{2} dx=\int_{2\pi}^{0}(2-sinx )^{2} dx=-9\pi.\] Since, the smooth parametrization of DO is \(0i + (2 \)-\( 2t)j\), so \[\int _{DO} y^{2} dx=\int_{0}^{0}y^{2} dx=\int_{0}^{1}(2-2t)^{2}\times 0 ~dt =0.\]4.2. Physical applications of line integral
In physics, the line integral is used, in particular, for computations of- mass of a wire,
- center of mass and moments of inertia of a wire,
- work done by a force on an object moving in a vector field,
- magnetic field around a conduct (Ampere\('\)s law),
- voltage generated in a loop (Faraday\('\)s law of magnetic induction).
4.2.1. Mass of a wire
Suppose that a piece of a wire is described by a curve \(C\) in three dimensions. The mass per unit length of the wire is a continuous function \(\rho(x, y, z).\) Then the total mass of the wire is expressed through the line integral of scalar function as [7] \begin{equation*} m=\int_{C} \rho(x,y,z)ds. \end{equation*} If \(C\) is a curve parameterized by the vector function \(r(t) = (x(t), y(t), z(t))\) on \([\alpha,~\beta],\) then the mass can be computed by the formula \begin{equation*} m =\int_{\alpha}^{\beta}\rho(x(t),y(t),z(t))\times\sqrt{(\frac{dx}{dt})^{2}+(\frac{dy}{dt})^{2}+(\frac{dz}{dt})^{2} )} dt\,. \end{equation*} If \(C\) is a curve in the \(xy-\)plane, then the mass of the wire is given by \[m=\int_{C} \rho(x,y)ds.\] Or in parametric form \begin{equation*} m =\int_{\alpha}^{\beta}\rho(x(t),y(t))\times\sqrt{(\frac{dx}{dt})^{2}+(\frac{dy}{dt})^{2} } dt\,. \end{equation*}Example 17. Consider a wire lying along the arc of the circle \(x^{2}+y^{2}=1\) from \(A(1, 0)\) to \(B(0, 1)\) with the density \(\rho(x, y) = xy\) (Figure 11).
Figure 11.
4.2.2. Center of mass and moments of inertia of a wire [7]
Let a wire is described by a curve \(C\) with a continuous density function \(\rho(x, y ,z).\) The coordinates of the center of mass of the wire are defined as \begin{equation*} \overline{x}=\frac{M_{yz}}{m},~ \overline{y}=\frac{M_{xz}}{m} ~and~ \overline{z}=\frac{M_{xy}}{m}\,, \end{equation*} where \begin{equation*} M_{yz} = \int_{C} x\rho(x,y,z)ds,~M_{xz}=\int_{C} y\rho(x,y,z)ds ~and~ M_{xy}=\int_{C} z\rho(x,y,z)ds \end{equation*} are so-called first moments. The moments of inertia about the \(x-\)axis, \(y-\)axis and \(z-\)axis are given by the formulas [7]- \(I_{x}=\int_{C} (y^{2}+z^{2})\rho(x,y,z)ds\),
- \(I_{y}=\int_{C} (x^{2}+z^{2})\rho(x,y,z)ds\),
- \(I_{z}=\int_{C} (x^{2}+y^{2})\rho(x,y,z)ds.\)
Example 18. Consider a circle \(x^{2} + y^{2} = a^{2}\) with the density \(\rho\) = 1. The parametric equation of this circle is\[ \begin{cases} x=a\cos t \\ y=a\sin t \end{cases} \] for \(0 \leq t \leq 2\pi\). Then the moment of inertia \(I_{x}\) about the \(x-\)axis is \begin{equation*} I_{x}=\int_{0}^{2\pi}(a\sin t)^{2}\times 1\times \sqrt{(-a\sin t)^{2}+(a\cos t)^{2}} dt=a^{3} \int_{0}^{2\pi}\sin^{2}t dt = \pi a^{3}\,. \end{equation*}
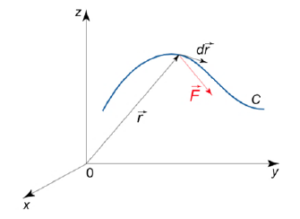
4.2.3. Work done by a force on an object moving in a velocity field [7]
Work done by a force \(F\) on an object moving along a curve \(C\) is given by the line integral \[W=\int_{C} F~.~dr\] where \(F\) is the vector force field acting on the object, dr is the unit tangent vector (Figure 12). The notation \(F . dr\) means dot product of \(F\) and \(dr.\)Figure 12.
Remark 9. The force field \(F\) is not necessarily the cause of moving the object. It might be some other force acting to overcome the force field that is actually moving the object. In this case the work of the force \(F\) could result in a negative value.
If a vector field is defined in the coordinate form \(F = (P(x, y, z), Q(x, y, z), R(x, y, z)),\) then the work done by the force is calculated by the formula
\begin{equation*} W=\int_{C} F ~. ~dr=\int_{C} [Pdx+Qdy+Rdz]. \end{equation*} If the object is moved along a curve \(C\) in the \(xy-\) plane, then the following formula is valid \begin{equation*} W=\int_{C} F~.~dr=\int_{C} [Pdx+Qdy] \end{equation*} where \(F = (P(x, y), Q(x, y)).\)If a path \(C\) is specified by a parameter \(t\) (\(t\) often means time), the formula for calculating work becomes
\begin{equation*} W = \int_{\alpha}^{\beta}[P(x(t),y(t),z(t)) \frac{dx}{dt} +Q(x(t),y(t),z(t)) \frac{dy}{dt}+R(x(t),y(t),z(t)) \frac{dz}{dt} ]dt\,, \end{equation*} where \(t\) goes from \(\alpha\) to \(\beta\). If a vector force field \(F\) is conservative, then the work on an object moving from \(A\) to \(B\) can be found by the formula \begin{equation*} W=u(B)-u(A)\,, \end{equation*} where \(u(x, y, z)\) is a scalar potential function of a vector force field \(F.\)Example 19. Consider a force field \(F(x, y) = (xy, x + y)\) on an object moving from the origin \(O(0, 0)\) to the point \(A(1, 1)\) along the path \(C.\)
- Assume \(C\) is the line segment \(y = x.\) The parametric equation of this line segment is \[ \begin{cases} x=t \\ y=t \end{cases} \] for \(0 \leq t \leq 1\). The work along the line segment \(y = x\) is \begin{equation*} W_{1}=\int_{C} [xydx+(x+y)dy]=\int_{0}^{1}[t^{2} +2t]dt=\frac{4}{3}. \end{equation*}
- Assume \(C\) is the curve \(y = \sqrt {x}\). The parametric equation of this line segment is \[ \begin{cases} x=t \\ y=\sqrt{t} \end{cases} \] for \(0 \leq t \leq 1\). The work along the line segment \(y = \sqrt{x}\) is \begin{equation*} W_{2}=\int_{C} [xydx+(x+y)dy]=\int_{0}^{1}[t^{\frac{3}{2}} +\frac{1}{2}(\sqrt{t}+1)]dt=\frac{37}{30}\,. \end{equation*}
Remark 10. For Example 19, if the force field is \(F(x, y) = xi + yj,\) then \(F\) is conservative force and in cases a and b, the work done is independent of the path i.e., \(W = f(1, 1)- f(0, 0) = 1\) where \(f(x, y) = \frac{x^{2}}{2} + \frac{y^{2}}{2} + c\) is a potential function for a force field \(F(x, y) = xi + yj.\)
4.2.4. Ampere\('\)s law [7]
The line integral of a magnetic field \(B\) around a closed path \(C\) is equal to the total current flowing through the area bounded by the contour \(C\) (Figure 13). This is expressed by the formula \begin{equation*} \oint_{C} B~.~dr= \mu_{0} I\,, \end{equation*} where \(\mu_{0}\) is the vacuum permeability constant, equal to \(4\pi \times 10^{-7} H/m \thickapprox 1.26\times 10^{-6} H/m.\)Figure 13.
Example 20. Let us develop the formula of the magnetic field in vacuum a distance \(r\) from the axis of a long straight wire carrying current \(I.\)
To find the field a distance \(r\) from the wire, we consider a loop of radius \(r,\) centered on the wire with its plane perpendicular to the wire with the current \(I\) (Figure 14). Since the field \(B\) has a constant magnitude and the field is tangent to the loop everywhere, the dot product of the vectors \(B\) and \(dr\) is just \(Bdr.\) Then we can write \begin{equation*} \oint_{C} B~.~dr=\oint_{C} Bdr=B\oint_{C} dr=B\int_{0}^{2\pi}dr=2\pi rB\,. \end{equation*} As a result, we have \(2\pi rB=\mu_{0} I \Longrightarrow B=\frac{\mu_{0} I}{2\pi r}\).Figure 14.
4.2.5. Faraday\('\)s law [7]
The electromotive force \(\epsilon\) induced around a closed loop \(C\) is equal to the rate of the change of magnetic flux passing through the loop (Figure 15). \begin{equation*} \epsilon=\oint_{C} E~.~dr=-\frac{d\psi}{dt}\,. \end{equation*}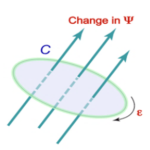
Figure 15.
Example 21. Let us evaluate the maximum electromotive force \(\epsilon\) and the electric field \(E\) induced in a finger ring of radius \(1cm\) when the passenger flies on an airplane in the magnetic field of the Earth with the velocity of \(900km/h.\)
According to Faraday\('\)s law, \begin{equation*} \epsilon=\oint_{C} E~.~dr=-\frac{d\psi}{ dt}\,. \end{equation*} As the conducting ring moves through the Earth magnetic field, there is a change in the magnetic flux \(\psi\), passing through the ring. Suppose that the magnetic field \(B\) is perpendicular to the plane of the ring. Then change in the flux for the time \(\vartriangle t\) is \begin{equation*} \vartriangle \psi=2rBx=2rBv\vartriangle t\,, \end{equation*} where \(x = v\vartriangle t, v\) is the velocity of the airplane and \(B\) is the magnetic field of the Earth. It follows from the last expression that \begin{equation*} \epsilon=-\frac{d\psi}{dt}=2rBv. \end{equation*} Substituting the given values \( v = 900km/h = 250m/s, r = 1cm = 0.01m\) and \(B = 5\times10^{-5} T\), we obtain the electromotive force \( \epsilon=2rBv=2 \times 0.01 \times 5\times 10^{-5} \times 250=0.00025V\). As it can be seen, it's safe for human.We can find the electric field in the conducting ring by the formula \(\epsilon=\oint_{C} E~.~dr\).
By symmetry, the induced electric field will have a constant magnitude along the ring. Its direction will be tangential to the circle at every point. Hence, the line integral around the circle is
\begin{equation*} \epsilon=\oint_{C} E~.~dr=\oint_{C} Edrcos0=E\oint_{C} dr=2\pi rE\,. \end{equation*} Hence, the electric field strength is \begin{equation*} E=\frac{\epsilon}{2\pi r}=\frac{0.00025}{2\pi \times 0.01}=0.00398V/m. \end{equation*}5. Summary
From this study, we acquire an idea regarding to line integral and its applications. Before we deal line integral, we need to have an idea regarding to space curves, and scalar and vector fields. As stated earlier, we deal line integral in either Cartesian plane or Complex plane. This integral has geometrical as well as physical applications.Acknowledgments First of all, I would like to thank my colleagues at Debark University for giving me their genuine advices and constructive comments from the very beginning of this study till its end. Secondly, my thanks also go to department of Mathematics, Debark University, which helped me in copying available hard materials and printing available soft copy materials for this study. Finally, I am deeply indebted to my wife Manayesh Melkamu for her encouragement to do this study and I would like to say God bless her.
Conflicts of Interest:
''The author declares no conflict of interest.''References
- Wikipedia. (2019). Line Integral. Retrieved on January 10/2019 from https://en.wikipedia.org/wiki/Line_-integral. [Google Scholor]
- Ellis, R., & Gulick, D. (1878). Calculus with Analytic Geometry, 3rd Edition. USA: Harcourt Brace Jovanovich, Inc.[Google Scholor]
- Moltot, B. (2016). A Hand Book of Applied Mathematics III. Ethiopia: ZA Printing Press. [Google Scholor]
- Wikipedia. (2017). Curve Orientation. Retrieved on March 7/2017 from https://en.wikipedia.org/wiki/curve_-orientation. [Google Scholor]
- Zill, D. G., & Shanahan, P. D. (2015). Complex Analysis: A First Course with Applications, 3rd edition. USA: Jones Bartlett Learning. [Google Scholor]
- Math24. (2018). Geometrical Applications of Line Integral. Retrieved on January 30/2018 from http://www.math24.net/geometric-applications-line-integrals. [Google Scholor]
- Math24. (2018). Physical Applications of Line Integral. Retrieved on January 30/2018 from https://www.math24.net/physical-applications-line-integrals. [Google Scholor]