Block Digraph of a Directed Graph

1. Introduction

For digraph theoretical terminologies and notations in this paper we follow the books [1, 2]. There are many (di)graph operators (or (di)graph valued functions) with which one can construct a new (di)graph from a given (di)graph, such as the line (di)graph, the total (di)graph, and their generalizations. One such generalization is the block graph concept whose properties and characterizations were considered in [3]. It is the object of this paper to extend the concept of block graph in a similar and natural way to the directed case and to develop some of the properties of the ''block digraph''.

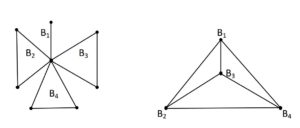
Let $G$ be a graph of order \(n\) \((n \geq 3)\). The block graph \(B(G)\) of \(G\) is that graph whose vertices are the blocks \(B_1,B_2,\ldots,B_N\) of \(G\) and whose edges are determined by taking two vertices \(B_i\) and \(B_j\) as adjacent if and only if they contain a cut-vertex of \(G\) in common. See Figure 1 for an example of a graph \(G\) and its block graph \(B(G)\).

2. Preliminaries

A directed graph (or just \(digraph\)) \(D\) consists of a finite non-empty set \(V(D)\) of elements called \(vertices\) and a finite set \(A(D)\) of ordered pairs of distinct vertices called \(arcs\). Here \(V(D)\) is the vertex set and \(A(D)\) is the arc set of \(D\). For an arc \((u,v)\) or \(uv\) in \(D\), the first vertex \(u\) is its \(tail\) and the second vertex \(v\) is its \(head\). A digraph without any arcs is said to be totally disconnected.
A digraph \(D=(V,A)\) is \(symmetric\) if \(xy \in A\) implies \(yx \in A\). A complete symmetric digraph is one which is both complete and symmetric. A complete symmetric digraph is denoted by \(\overleftrightarrow{K_p}\), where \(p\) is the number of vertices in the digraph. A digraph \(D\) is strongly connected (or \(strong\), for short) if for any two vertices \(u\) and \(v\) of \(D\), there are a directed path from \(u\) to \(v\) and a directed path from \(v\) to \(u\). It follows that every complete symmetric digraph is strong, but not every strong digraph is complete symmetric. A cut-set of a digraph \(D\) is defined as a minimal set of vertices whose removal increases the number of connected components of \(D\). A cut-set of size one is called a cut-vertex.
By a subgraph of a digraph \(D\) we mean a digraph whose vertices and arcs are vertices and arcs of \(D\). A subgraph with a certain special property is said to be maximal with respect to that property if no larger subgraph (i.e., with more vertices or arcs) contains it as a subgraph and has the property. For more details on maximal with respect to other special properties see the book [2].

A block \(B\) of a digraph \(D\) is a maximal weak subgraph of \(D\), which has no vertex \(v\) such that \(B-v\) is disconnected. An entire digraph is called a block if it has only one block.

Definition Let \(D\) be a digraph with \(n\) vertices \(v_1,v_2,\ldots,v_n\) and \(m\) arcs, and \(L(D)\) its associated line digraph with \(n^{'}\) vertices and \(m^{'}\) arcs. We have \(n^{'}=m\) and \(m^{'}=\displaystyle \sum_{i=1}^{n} d^{-}(v_i)\cdot d^{+}(v_i)\). Furthermore, the in-degree and out-degree of a vertex \(v^{'}=(v_i,v_j)\) in \(L(D)\) are \(d^{-}(v^{'})=d^{-}(v_{i})\) and \(d^{+}(v^{'})=d^{+}(v_{j})\), respectively.

Definition Let \(D\) be a connected digraph of order \(n\) \((n \geq 3)\) and let \(B(D)=\{B_1,B_2,\ldots,B_N\}\) be a set of blocks of \(D\). The block digraph \(Q=\mathbb{B}(D)\) has vertex set \(V(Q)=B(D)\) and arc set \(A(Q)=\{ B_iB_j: B_i,B_j \in V(Q); B_i,B_j \text{ have a cut-vertex of }D\text{ in common and every vertex of }B_j\text{ is reach}\\ \text{-able from every other vertex of }B_i\}.\)

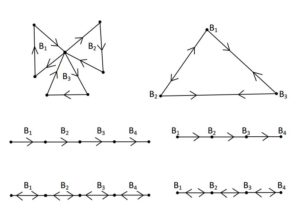
Note that \(\mathbb{B}(D)\) is defined only for digraphs which have at least two blocks. Furthermore, the block digraph \(\mathbb{B}(D)\) of a digraph \(D\) is symmetric if \(D\) is strong with at least one cut-vertex (or at least two blocks). In Figure 2, three different digraphs on the left and their corresponding block digraphs \(\mathbb{B}(D)\) on the right are shown.

3. Properties of \(\mathbb{B}(D)\)

property 4.1. If \(D\) is strong and the number of cut-vertices is at least two, then the size of \(\mathbb{B}(D)\) equals the twice the number of cut-vertices of \(D\) (see the third example of Figure 2).

property 4.2. If \(D\) is strong with a unique cut-vertex, then \(\mathbb{B}(D) \cong \overleftrightarrow{K_p}\) (see the first example of Figure 2).

property 4.3. If \(D\) is a directed path of order \(n\) \((n \geq 3)\), then \(\mathbb{B}(D) \cong L(D)\), where \(L(D)\) is the line digraph of \(D\) (see the second example of Figure 2).

4. Characterization of \(\mathbb{B}(D)\)

Theorem 4.1. The block digraph \(\mathbb{B}(D)\) of a digraph \(D\) is complete symmetric if and only if \(D\) is strong with a unique cut-vertex.

Proof. Suppose \(\mathbb{B}(D)\) is complete symmetric. Assume that \(D\) is strong. Let \(C_1\) and \(C_2\) be the cut-vertices of \(D\); and let \(B_1,B_2,B_3\) be the blocks of \(D\) such that \(B_1\) and \(B_2\) contain \(C_1\) in common; \(B_2\) and \(B_3\) contain \(C_2\) in common. Then the block vertex \(B_1\) is neither adjacent to nor adjacent from \(B_3\) in \(\mathbb{B}(D)\), which contradicts the assumption that \(\mathbb{B}(D)\) complete symmetric.
Conversely, suppose that \(D\) is strong with a unique cut-vertex, say \(C\). Let \(B_1,B_2,\ldots,B_N\) be blocks of \(D\). Clearly, every block of \(D\) contain \(C\) in common. By definition, every pair of vertices of \(\mathbb{B}(D)\) are joined by two arcs, one in each direction. Thus \(\mathbb{B}(D)\) is complete symmetric (for example, see the first example of Figure 2). This completes the proof.

Note that since every complete symmetric digraph is a block, by Theorem 4.1, the block digraph \(\mathbb{B}(D)\) of a digraph \(D\) is a block if \(D\) is strong with a unique cut-vertex.

Definition 4.2. A digraph \(D\) is said to be \(Eulerian\) if it contains a closed walk which traverses every arc of \(D\) exactly once. Such a walk is called an Euler walk.

The following result characterizes Eulerian digraphs.

Theorem 4.3. (Gutin [1]): A directed graph \(D=(V,A)\) is Eulerian if and only if \(D\) is connected and \(d^{-}(u)=d^{+}(u)\) for all \(u \in V(D)\).

Theorem 4.4. The block digraph \(\mathbb{B}(D)\) of a digraph \(D\) is Eulerian if and only if every block of \(D\) is strong.

Proof. Suppose \(\mathbb{B}(D)\) is Eulerian. Assume that there is a non-strong block \(B\) of \(D\). Let \(B_1\) be a block of \(D\) which shares a cut-vertex \(C\) with \(B\). Then there exists a vertex in \(B\), which is not reachable from \(C\). By definition, \(\mathbb{B}(D)\) contains two isolated vertices with no arcs, i.e., \(\mathbb{B}(D)\) is disconnected of order two, which contradicts the assumption that \(\mathbb{B}(D)\) is Eulerian.
Conversely, suppose that every block of \(D\) is strong. We consider the following two cases.
Case 1: Assume that the number of cut-vertices of \(D\) is exactly one. By property 3.2, \(\mathbb{B}(D)\) is isomorphic to \(\overleftrightarrow{K_p}\), which is complete symmetric. Clearly, the in-degree of each vertex equals its out-degree in \(\mathbb{B}(D)\). By Theorem 4.3, \(\mathbb{B}(D)\) is Eulerian.
Case 2: Assume that the number of cut-vertices of \(D\) is at least two. Then \(\mathbb{B}(D)\) is symmetric. Therefore, the in-degree of each vertex equals its out-degree in \(\mathbb{B}(D)\). By Theorem 4.3, \(\mathbb{B}(D)\) is Eulerian. This completes the proof. \end{proof}

Definition 4.5. A spanning directed path of a digraph is called a Hamiltonian path and a spanning cycle a Hamiltonian cycle. A digraph containing a Hamiltonian cycle is said to be \(Hamiltonian\).

Theorem 4.6.(Gutin [1]): Every strong connected tournament has a Hamiltonian cycle.

Theorem 4.7. The block digraph \(\mathbb{B}(D)\) of a digraph \(D\) is Hamiltonian if \(D\) is strong with a unique cut-vertex.

Proof. Suppose that \(D\) is strong with a unique cut-vertex. By Theorem 4.1, the block digraph \(\mathbb{B}(D)\) is complete symmetric. Furthermore, since every complete symmetric digraph is strong, Theorem 4.6 implies that \(\mathbb{B}(D)\) contains a Hamiltonian cycle. Therefore, \(\mathbb{B}(D)\) is Hamiltonian. This completes the proof.

Definition 4.8. The least number of edge crossings of a graph \(G\), among all planar embeddings of \(G\), is called the crossing number of \(G\) and is denoted by \(cr(G)\). A graph is \(planar\) if it has a drawing without crossings. A graph that is not planar is called \(nonplanar\).

Kulli [4] introduced the the concept of non-zero inner vertex number of a planar graph.

Definition 4.9. A positive integer \(r\) such that any plane embedding of a planar graph \(G\) has at least \(r\) vertices in the interior region of \(G\) is called the inner vertex number of \(G\) and is denoted by \(i(G)\).

In general, the planar graphs having \(i(G) = r, r > 0\) are called r-nonouterplanar graphs. In particular, zero-nonouterplanar graphs are called outerplanar graphs and one-nonouterplanar graphs are called minimally nonouterplanar graphs. That is, a graph \(G\) is said to be outerplanar if \(i(G)=0\) and minimally nonouterplanar if \(i(G)=1\). An outerplanar graph \(G\) is maximal outerplanar if no edge can be added without losing outerplanarity. Digraphs that can be drawn without crossings between arcs (except at end vertices) are called planar digraphs. Clearly this property does not depend on the orientation of the arcs and hence we ignore the orientation while defining the planarity; outerplanarity; maximal outerplanarity; and minimally nonouterplanarity of a digraph. Furthermore, since most of the results and definitions of undirected graphs are valid for planar digraphs as far as their underlying graphs are concerned, the following definitions hold good for planar digraphs. A digraph \(D\) is said to be \(outerplanar\) if \(i(D)=0\) and minimally nonouterplanar if \(i(D)=1\). Finally, the following Theorem can be used to check the maximal outerplanar property of a digraph.

Theorem 4.10. (F. Harary [5]) Every maximal outerplanar graph \(G\) with \(n\) vertices has \(2n-3\) edges.

We now assume that \(D\) is ''strongly connected'' in order to study the planarity; outer planarity; and minimally nonouterplanarity properties of \(\mathbb{B}(D)\). We further assume that \(\psi(D)\) is the number of blocks of \(D\) containing a cut-vertex of \(D\) in common. For example, \(\psi(D)=3\) for the first example; \(\psi(D)=0\) for both second and third examples of Figure 2. Furthermore, it should be noted that \(\psi(D)\) must be at least two in order to study the properties mentioned above.

Theorem 4.11. The block digraph \(\mathbb{B}(D)\) of \(D\) is planar if and only if \(\psi(D)\) is at most four.

Proof. Suppose \(\mathbb{B}(D)\) is planar. Assume that \(\psi(D) \geq5\). If \(\psi(D)=5\), then \(\mathbb{B}(D)=\overleftrightarrow{K_5}\). Hence cr\((\mathbb{B}(D))>0\), which contradicts the assumption that \(\mathbb{B}(D)\) is planar.\\ Conversely, suppose that \(\psi(D)\) is at most four. For \(\psi(D)=2,3,\) and \(4\), \(\mathbb{B}(D)\) is \(\overleftrightarrow{K_2}, \overleftrightarrow{K_3}\), and \(\overleftrightarrow{K_4}\), respectively. Clearly, cr\((\mathbb{B}(D))=0\). Hence \(\mathbb{B}(D)\) is planar.

Theorem 4.12. The block digraph \(\mathbb{B}(D)\) of \(D\) is outerplanar if and only if \(\psi(D)\) is at most three.

Proof. Suppose \(\mathbb{B}(D)\) is outerplanar. Assume that \(\psi(D) \geq4\). If \(\psi(D)=4\), then \(\mathbb{B}(D)=\overleftrightarrow{K_4}\). Hence \(i(\mathbb{B}(D))=1\), which contradicts the assumption that \(\mathbb{B}(D)\) is outerplanar.
Conversely, suppose that \(\psi(D)\) is at most three. For \(\psi(D)=2\) and 3, \(\mathbb{B}(D)\) is \(\overleftrightarrow{K_2}\) and \(\overleftrightarrow{K_3}\), respectively. Clearly, \(i(\mathbb{B}(D))=0\). Hence \(\mathbb{B}(D)\) is outerplanar.

Theorem 4.13. The block digraph \(\mathbb{B}(D)\) of \(D\) is minimally nonouterplanar if and only if \(\psi(D)\) is exactly four.

Proof. Suppose \(\mathbb{B}(D)\) is minimally nonouterplanar. Assume that \(\psi(D) \geq 5\). By Theorem 4.11, \(\mathbb{B}(D)\) is nonplanar, a contradiction. On the other hand, suppose that \(\psi(D)\) is either two or three. By Theorem 4.12, \(\mathbb{B}(D)\) is outerplanar, again a contradiction.
Conversely, suppose that \(\psi(D)\) is exactly four. By necessity of Theorem 4.12, the inner vertex number of \(\mathbb{B}(D)\) is one, i.e., \(i(\mathbb{B}(D))=1\). Hence \(\mathbb{B}(D)\) is minimally nonouterplanar.

\end{proof} We now investigate the maximal outerplanar property of \(\mathbb{B}(D)\). Here \(D\) need not be strongly connected.

Theorem 4.14. The block digraph \(\mathbb{B}(D)\) of \(D\) is maximal outerplanar if and only if \(D=\vec{P_3}\), i.e., a directed path of order three.

Proof. Suppose \(\mathbb{B}(D)\) is maximal outerplanar. Assume that \(D\) is a directed path \(\vec{P_n}\), \(n \geq 4\). By Property 3.3, \(\mathbb{B}(D) \cong L(D) \cong \vec{P_n}\), \(n \geq 3\). Clearly the order and size of \(\vec{P_n}\), \(n \geq 3\), are \(\alpha+2\) and \(\alpha+1\), respectively, where \(\alpha=(n-3)\), \(n \geq 4\). But \(\alpha+1< 2\alpha+1=2(\alpha+2)-3\). Since \(\mathbb{B}(D)\) has \(\alpha+1\) arcs, Theorem 4.10 implies that \(\mathbb{B}(D)\) is not maximal outerplanar, a contradiction.
Conversely, suppose that \(D=\vec{P_3}\). By definition, \(\mathbb{B}(D)=\vec{P_2}\). By Theorem 4.10, \(\mathbb{B}(D)\) is maximal outerplanar. This completes the proof. \end{proof}

Competing Interests

The author(s) do not have any competing interests in the manuscript.

Acknowledgments

The authors wish to thank the referees for the valuable comments and suggestions which led to an improved version of the paper.