Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2019.0056
3-total edge mean cordial labeling of some standard graphs
Department of Mathematics, University of Management and Technology, Lahore Pakistan.; (F.A & Z.Z & S.Z)
\(^{1}\)Corresponding Author: zohaib_zahid@hotmail.com
Abstract
Keywords:
1. Introduction
We begin with finite, undirected, simple and connected graph \(\mathcal{G}=(V_{\mathcal{G}},E_{\mathcal{G}})\). The set \(V_{\mathcal{G}}\) is called vertex set and the set \(E_{\mathcal{G}}\) is called edge set of graph \(\mathcal{G}\). Order of a graph is the number of vertices in \(\mathcal{G}\) and size of a graph is the number of edges in \(\mathcal{G}\). We follow the standard notations and terminology of graph theory as in [1]. Graph labeling were first introduced in the late \(1960's\). A graph labeling is an assignment of integers to the vertices or edges or both subject to certain condition(s). If the domain of mapping is the set of vertices (or edges) then the labeling is called a vertex labeling (or an edge labeling). We have the following notations, in order to know cordial labeling \(\alpha\) and its sorts .- The number of vertices labeled by \(x\) is \(v_{\alpha} (x)\);
- The number of edges labeled by \(x\) is \(e_{\alpha} (x)\);
- \(v_{\alpha}(x,y)=v_{\alpha}(x)-v_{\alpha}(y)\);
- \(e_{\alpha}(x,y)=e_{\alpha}(x)-e_{\alpha}(y)\);
- \(s(x)\)=\(v_{\alpha}(x) + e_{\alpha}(x)\);
- \(\mathbb{Z}_k\) denotes the first \(k\) non negative integers, i.e \(\mathbb{Z}_k=\{0,1,\ldots,k-1\}.\)
Definition 1. Let \({\alpha}: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) as \({\alpha}^*(uv)=|{\alpha}(u)-{\alpha}(v)|\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called cordial labeling if \(|v_{\alpha}(1,0)|\leq1\) and \(|e_{\alpha}(1,0)|\leq1\).
Definition 2. Let \({\alpha}: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) as \({\alpha}^*(uv)={\alpha}(u){\alpha}(v)\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called product cordial labeling if \(|v_{\alpha}(1,0)|\leq1\) and \(|e_{\alpha}(1,0)|\leq1\). For details see [3].
Definition 3. Let \({\alpha}: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) as \({\alpha}^*(uv)={\alpha}(u){\alpha}(v)\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called total product cordial labeling if \(|s(0)-s(1)|\leq1\). For details see [4, 5.
Definition 4. Let \( {\alpha}:V_{\mathcal{G}} \rightarrow\mathbb{Z}_k\), \(2\leq k\leq|E_{\mathcal{G}}|\) be a mapping that induces \({\alpha}^*: E_{\mathcal{G}}\rightarrow\mathbb{Z}_k\) as \({\alpha}^*(uv)={\alpha}(u){\alpha}(v)\) \((\text{mod}k)\) where \(uv \in E_{\mathcal{G}}\). Then \({\alpha}\) is called a k-total product cordial labeling if \(|s(a)-s(b)|\leq1\) for all \(a,b\in\mathbb{Z}_k\). For details see [6].
Definition 5. Let \( {\alpha}:E_{\mathcal{G}} \rightarrow\mathbb{Z}_2\) be a mapping that induces \({\alpha}^*: V_{\mathcal{G}}\rightarrow\mathbb{Z}_2\) such that \({\alpha}^*(u)={\alpha}(e_1){\alpha}(e_2) \ldots {\alpha}(e_n)\) for edges \(e_1,e_2,\ldots,e_n \) incident to \(u\), then \({\alpha}\) is called edge product cordial labeling if \(|v_{\alpha}(0,1)|\leq1\) and \(|e_{\alpha}(0,1)|\leq1\). For details see [7, 8]VB4,VB1}.
Definition 6. Let \({\alpha} : E_{\mathcal{G}} \rightarrow \mathbb{Z}_2\) be a mapping that induces \({\alpha}^* : V_{\mathcal{G}} \rightarrow \mathbb{Z}_2\) such that \({\alpha}^*(u)={\alpha}(e_1){\alpha}(e_2) \ldots {\alpha}(e_n)\) for edges \(e_1,e_2,\ldots,e_n \) that are incident to \(u\), then \({\alpha}\) is called a total edge product cordial labeling if \(|s(0)-s(1)|\leq1\). For details see [9, 10].
Definition 7. Let \({\alpha}:E_{\mathcal{G}} \longrightarrow\mathbb{Z}_k\), \( 2\leq k\leq|E_{\mathcal{G}}|\) be a mapping that induces \({\alpha}^*:V_{\mathcal{G}} \longrightarrow\mathbb{Z}_k\) such that \({\alpha}^*(u)={\alpha}(e_1){\alpha}(e_2) \ldots {\alpha}(e_n)\)(mod \(k\)) for edges \(e_1,e_2,\ldots,e_n \) incident to \(u\), then \({\alpha}\) is called \(k\)-total edge product cordial labeling if it satisfy \(|s(a)-s(b)|\leq1\) for all \(a,b\in\mathbb{Z}_k\). For details see [11, 12, 13, 14, 15, 16, 17, 18, 19].
Motivated by the above definitions, we introduce new labeling named k-total edge mean cordial labeling which is defined as:Definition 8. Let \({\alpha}: E_G\longrightarrow\mathbb{Z}_k\) be a mapping that induces \({\alpha}^*:V_G\longrightarrow\mathbb{Z}_k\) such that for each vertex \(u\), \({\alpha}^*(u)\) =\(\lceil\ {\alpha}(e_1)+{\alpha}(e_2)\ldots+{\alpha}(e_n) /n\rceil\),\ where \(e_1\), \(e_2\),\ldots, \(e_n\) are incident with \(u\) then \({\alpha}\) is called k-total edge mean cordial labeling (k-TEMC) if \(|s(i)-s(j)|\leq 1\) where \(i,j\in\mathbb{Z}_k\). A graph with a \(k\)-total edge mean cordial labeling is called \(k\)-total edge mean cordial graph.
The rest of the paper is structured as follows: In Section 2, 3-TEMC labeling of path is discussed. Section 3 devoted to the study 3-TEMC labeling of double comb graph. In Section 4, we study ladder graph and its 3-TEMC labeling. In Section 5, 3-TEMC labeling of fan graph is discussed.2. 3-TEMC labeling of path graph
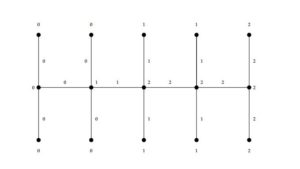
A path graph \(P_n\) is a graph whose vertices can be listed in the order \(u_1,u_2,u_3,\ldots, u_n\) such that the edges are \(u_1u_2,u_2u_3,\ldots,u_{n-1}u_n\). Here \(V_{P_n}= \{u_i : 1\leq i \leq n\}\) and \( E_{P_n}= \{e_i=u_i u_{i+1} : 1\leq i \leq n-1\}\). (see Figure 1).Figure 1. Path graph \(P_6\).
Theorem 9. Any path \(P_n\) for \(n\geq3\) admits 3-TEMC labeling.
Proof.
The following cases should be considered in order to prove that \(P_n\) is 3-TEMC.
Case 1. If \(n\equiv0 \text{ (mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(P_3\) (see Figure 2).
Figure 3. 3-TEMC labeling of \(P_3\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q-1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 2q, & \text{ if \(i=0,1\)}\\ 2q-1, & \text{if \(i=2.\)} \end{cases}\).Case 2. Let \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(P_4\) (see Figure 3).
Figure 3. 3-TEMC labeling of \(P_4\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 2q, & \text{ if \(i=0,1\)}\\ 2q+1, & \text{if \(i=2.\)} \end{cases}\).Case 3. If \(n\equiv2 \text{ (mod }3)\) then \(n= 3q+2\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(P_5\) (see Figure 4).
Figure 4. 3-TEMC labeling of \(P_5\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+3\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) and \(\alpha(e_{q+2})=0\), \(\alpha(e_{q+1})=1\).
Hence \(\alpha\) is 3-TEMC labeling because \(s(i)= 2q+1,\) for all \(i=0,1,2.\) Hence \(P_n\) have 3-TEMC labeling for \(n\geq2\).
3. 3-TEMC labeling of ladder graph
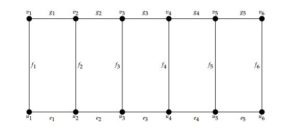
The ladder graph \(L_n\) is defined as the cartesian product of \(P_n\) by \(K_2\) where \(P_n\) is a path with \(n\) vertices and \(K_2\) is a complete graph with two vertices. Here \(V_{L_n}= \{{u_i,v_i : 1\leq i \leq n}\)\} and \( E_{L_n}= \{e_i=u_iu_{i+1}: 1\leq i \leq n-1\}\cup\{f_i=u_iv_i, 1\leq i \leq n\}\cup\{g_i=v_iv_{i+1}: 1\leq i \leq n-1\}\)(see Figure 5).Figure 5. Ladder graph \(L_{6}\).
Theorem 10. Let \(L_n\) be a ladder graph, then \(L_n\) admits 3-TEMC labeling.
Proof.
The following cases should be considered in order to prove that \(L_n\) is 3-TEMC.
Case 1. If \(n\equiv0 \text{ (mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\).
For \(q=1\), we have the following labeling of \(L_3\) (see Figure 6).
Figure 6. 3-TEMC labeling of \(L_3\).
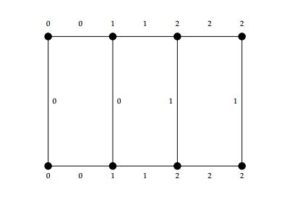
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q-1; \)}\\ 2, & \text{if \( 2q\leq i \leq 3q-1. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q-1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q, & \text{ if \(i=0\)}\\ 5q-1, & \text{if \(i=1,2.\)} \end{cases}\)Case 2. If \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(L_4\) (see Figure 7).
Figure 7. 3-TEMC labeling of \(L_4\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+1. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=5q+1\), for all \(i=0,1,2.\) For \(q=1\), we have the following labeling of \(L_5\) (see Figure 8).
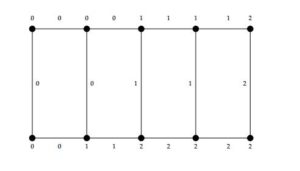
Figure 8. 3-TEMC labeling of \(L_5\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q+1. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+2. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q+3, & \text{ if \(i=0,1\)}\\ 5q+2, & \text{if \(i=2.\)} \end{cases}\) Hence the ladder graph \(L_n\) have 3-TEMC labeling.
4. 3-TEMC labeling of double comb graph
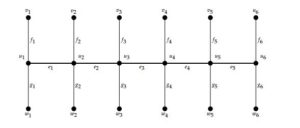
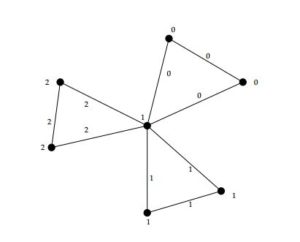
Double comb graph \(DCO_n\) is a graph achieved by unification of two pendant edges \(u_iv_i\) and \(u_iw_i\) to every vertex \(u_i\) of a path graph. Here \(V_{DCO_n}= V_{P_n}\cup\{{v_i,w_i : 1\leq i \leq n}\)\} and \(E_{DCO_n}= E_{P_n}\cup\{{f_i=u_iv_i, g_i=u_iw_i : 1\leq i \leq n}\}\) (see Figure 9).Figure 9. Double comb graph \(DCO_{6}\).
Theorem 11. Let \(DCO_n\) be a double comb graph, then \(DCO_n\) admits 3-TEMC labeling.
Proof. The following cases should be considered in order to prove that \(DCO_n\) is 3-TEMC. \begin{description}Case 1. If \(n\equiv0 \text{ (mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1\), we have the following labeling of \(DCO_3\) (see Figure 10).
Figure 10. 3-TEMC labeling of \(DCO_3\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q-1. \)} \end{cases}\) \(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\)\(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 6q, & \text{ if \(i=0,1\)}\\ 6q-1, & \text{if \(i=2.\)} \end{cases}\)Case 2. If \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(DCO_4\) (see Figure 11).
Figure 11. 3-TEMC labeling of \(DCO_4\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q-1; \)}\\ 1, & \text{if \( q\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+1; \)}\\ 2, & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 6q+2, & \text{ if \(i=0,1\)}\\ 6q+1, & \text{if \(i=2.\)} \end{cases}\)Case 3. If \(n\equiv2 \text{ (mod }3)\) then \(n= 3q+2\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(DCO_5\) (see Figure 12).
Figure 12. 3-TEMC labeling of \(DCO_5\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q+1. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+2. \)} \end{cases}\) \(\alpha(g_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q+1; \)}\\ 1, & \text{if \( q+2\leq i \leq 2q+2; \)}\\ 2, & \text{if \( 2q+3\leq i \leq 3q+2. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 6q+4, & \text{ if \(i=0,1\)}\\ 6q+3, & \text{if \(i=2.\)} \end{cases}\) Hence the double comb graph \(DCO_n\) have 3-TEMC labeling.
5. 3-TEMC labeling of fan graph
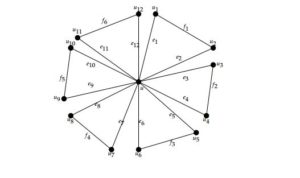
A Fan graph \(F_n\) is the graph obtained by taking \(n\) copies of the cycle graph \(C_3\) with a vertex \(u\) in common. Here \(V_{F_n} = \{{uu_i : 1\leq i \leq 2n}\)\} and \(E_{F_n} = {\{e_i=uu_i : 1\leq i \leq 2n}\}\cup\{{f_i = u_iu_{i+1} : 1\leq i \leq n-1} \text{ and } i \text{ is odd} \}\) (see Figure 13).Figure 13. Fan graph \(F_6\).
Theorem 12. Fan graph \(F_n\) for \(n\geq2\) admits 3-TEMC labeling.
Proof.
The following cases should be considered in order to prove that \(F_n\) is 3-TEMC.
Case 1. Let \(n\equiv1 \text{(mod }3)\) then \(n= 3q\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(F_3\) (see Figure 14).
Figure 14. 3-TEMC labeling of \(F_3\).
\(\alpha(e_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq 2q; \)}\\ 1, & \text{if \( 2q+1\leq i \leq 4q; \)}\\ 2, & \text{if \( 4q+1\leq i \leq 6q. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0, & \text{if \( 1\leq i \leq q; \)}\\ 1, & \text{if \( q+1\leq i \leq 2q; \)}\\ 2, & \text{if \( 2q+1\leq i \leq 3q. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q, & \text{ if \(i=0,2\)}\\ 5q+1, & \text{if \(i=1.\)} \end{cases}\)
Case 2. Let \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+1\), where \(q\in \mathbb{Z}^+\). For \(q=1,\) we have the following labeling of \(F_4\) (see Figure 15).
Figure 15. 3-TEMC labeling of \(F_4\).
\(\alpha(e_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq 2q+2; \)}\\ 1 & \text{if \( 2q+3\leq i \leq 4q+1; \)}\\ 2 & \text{if \( 4q+2\leq i \leq 6q+2. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq q; \)}\\ 1 & \text{if \( q+1\leq i \leq 2q+1; \)}\\ 2 & \text{if \( 2q+2\leq i \leq 3q+1. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=5q+2,\) for all \(i=0,1,2.\)
Case 3. If \(n\equiv1 \text{ (mod }3)\) then \(n= 3q+2\), where \(q\in \mathbb{Z}^+\). we have the following labeling of \(F_2\) (see Figure 16).
Figure 16. 3-TEMC labeling of \(F_2\).
\(\alpha(e_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq 2q+1; \)}\\ 1 & \text{if \( 2q+2\leq i \leq 4q+3; \)}\\ 2 & \text{if \( 4q+4\leq i \leq 6q+4. \)} \end{cases}\)\(\alpha(f_i)=\begin{cases} 0 & \text{if \( 1\leq i \leq q+1; \)}\\ 1 & \text{if \( q+2\leq i \leq 2q+1; \)}\\ 2 & \text{if \( 2q+2\leq i \leq 3q+2. \)} \end{cases}\) Hence \(\alpha\) is 3-TEMC labeling because \(s(i)=\begin{cases} 5q+3, & \text{ if \(i=0\)}\\ 5q+4, & \text{if \(i=1,2.\)} \end{cases}\) Hence the fan graph \(F_n\) have 3-TEMC labeling for \(n\geq2\).
Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- West, D. B. (1996).Introduction to graph theory (Vol. 2). Upper Saddle River, NJ: Prentice hall. [Google Scholor]
- Cahit, I. (1987). Cordial graphs-a weaker version of graceful and harmonious graphs.Ars combinatoria, 23 , 201-207. [Google Scholor]
- Sundaram, M., Ponraj, R., & Somasundaram, S. (2004). Product cordial labeling of graphs.Bull. Pure and Applied Sciences (Mathematics & Statistics) E, 23 , 155-163. [Google Scholor]
- Lai, Y. L., & Chen, Y. M., On the total product cordial labeling of \(P_n+ mK_1\).National Chiayi University.
- Sundaram, M., Ponraj, R., & Somasundram, S. (2006). Total product cordial labeling of graphs.Bulletin of pure & applied sciences. Sec. E, Mathematics & statistics, 25 , 199-203. [Google Scholor]
- Ponraj, R., Sundaram, M., & Sivakumar, M. (2012). K-total product cordial labelling of graphs.Applications and Applied Mathematics, 7 , 708-716. [Google Scholor]
- Vaidya, S. K., & Dani, N. A. (2010). Some new product cordial graphs.International Journal of Computing Science and Mathematics, 8 (4), 62-65.[Google Scholor]
- Vaidya, S. K., & Barasara, C. M. (2012). Edge product cordial labeling of graphs.Journal of Mathematical and computational Science, 2 (5), 1436-1450. [Google Scholor]
- Vaidya, S. K., & Barasara, C. M. (2013). Some new families of edge product cordial graphs.Advanced Modeling and Optimization, 15 (1), 103-111. [Google Scholor]
- Vaidya, S. K., & Barasara, C. M. (2013). Total edge product cordial labeling of graphs.Malaya Journal of Matematik, 3 (1), 55-63.[Google Scholor]
- Ahmad, Y., Ali, U., Zafar, S., & Zahid, Z. (2017). Some new standard graphs labeled by 3–total edge product cordial labeling.Applied Mathematics and Nonlinear Sciences, 2 (1), 61-72. [Google Scholor]
- Ahmad, A., Bača, M., Naseem, M., & Semaničová-Feňovčíková, A. (2017). On 3-total edge product cordial labeling of honeycomb.AKCE International Journal of Graphs and Combinatorics, 14 (2), 149-157.[Google Scholor]
- Ali, U., Bilal, M., Zafar, S., & Zahid, Z. (2017). Some Families of Convex Polytopes Labeled by 3-Total Edge Product Cordial Labeling.Punjab University Journal of Mathematics, 49 , 119-132. [Google Scholor]
- Azaizeh, A., Hasni, R., Ahmad, A., & Lau, G. C. (2015). 3-Totat edge product cordial labeling of graphs.Far East journal of Matheimatical sciences 96 (2), 193-209.
- Hasni, R., & Azaizeh, A. (2016). 3-total edge product cordial labeling of wheel related graphs.Matematika, 32 (2), 93-102. [Google Scholor]
- Ivanco, J. (2017). On 3-total edge product cordial connected graphs.Opuscula Mathematica, 37 (5), 725-734. [Google Scholor]
- Ivanco, J. (2017). On k-total edge product cordial graphs.The Australasian Journal of Combinatorics, 67 , 476-485.[Google Scholor]
- Kuo, D., Chang, G. J., & Kwong, Y. H. (1997). Cordial labeling of $mK_n.$Discrete Mathematics, 169 (1-3), 121-131.[Google Scholor]
- Yan, L., Li, Y., Zhang, X., Saqlain, M., Zafar, S., & Farahani, M. R. (2018). 3-total edge product cordial labeling of some new classes of graphs.Journal of Information and Optimization Sciences, 39 (3), 705-724.[Google Scholor]