Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2020.0104
An algorithm for choosing best shape parameter for numerical solution of partial differential equation via inverse multiquadric radial basis function
Kazeem Issa\(^1\), Sulaiman M. Hambali, Jafar Biazar
Department of Statistics and Mathematical Sciences, Kwara State University, Malete, Nigeria.; (K.I & S.M.H)
Department of Mathematical Sciences, University of Guilan, Rasht, Iran.; (J.B)
\(^{1}\)Corresponding Author: issa.kazeem@kwasu.edu.ng
Abstract
Keywords:
1. Introduction
RBF is an important method for approximating and interpolating functions and solving differential equations (both ordinary and partial) for data with scattered node locations and in computation domain in higher dimensions as discussed in [1]. RBF methods were first introduced by [2], who was a geodesist at Iowa State University. In his proposed method, he simplified the computation of scattered data problem relative to the previously used polynomial interpolation. In many cases, RBF methods have been proved to be effective, where polynomial interpolation fails. RBF method are often used in topographical representation and other intricate \(3D\) shapes.
The use of RBF to interpolate scattered data problem emanated from the fact that the interpolation problem becomes insensitive to the dimension (\(d\)) of the space in which the data set lies. Recently, different RBF based methods have gained attention in scientific, computing and engineering applications such as functions interpolation [3, 4], numerical solutions to partial differential equation (PDEs) [5, 6, 7], Multivariate scattered data processing [8] and so on. The main advantages of this method are spectral convergence rates that can be achieved using infinitely smooth basis functions, geometrical flexibility and ease of implementation [9, 10].
1.1. Idea of radial basis functions
The origin of RBFs can be traced back to [2], when Hardy introduced RBF multi-quadratics (MQ) to solve surface fitting on topography and irregular surfaces. As a field engineer from 1947 to 1951, Hardy was first interested in stream and ridge lines. Hardy believed that an interpolation method containing an exact fit of data to a topographical region should exist. After thorough investigation, he discovered what later become multiquadric (MQ). Prior to the knowledge of MQ, trigonometric and algebraic polynomials were employed. Due to the quadric surface, Hardy termed his method multiquadric. The MQ transformed scattered data to a very accurate fit model of graph or surface. Subsequently he considered the MQ as a consistent solution of biharmonic solution [10] to physically demonstrate its bravery. Other researchers like [11] extensively tested twenty-nine different algorithms on the typical benchmark function on interpolation problems and ranked the MQ-RBF and thin-plate splines TPS-RBF (introduced in [12] via employing the minimum bending energy theory of the surface of a thin plate) as top two candidates based on the following criteria: timing, storage, accuracy, visual pleasantness of the surface, and ease of implementation. Following the success recorded on researches, RBFs have become popular in the scientific computing world, such as computer graphics, data processing, and economics.
In 1986, Charles Micchelli developed the theory behind the MQ method, and proved that the MQ method matrix system is invertible [13]. Few years later, [14, 15] a collocating method was derived for solving partial differential equations using MQ. The breakthrough by Kansa triggered a research boom in RBF. The Kansa method is meshless and superior to the classical method due to some advantages such as: integration-free, ease of implementation and superior convergence. In addition, it may be of interest that even before Kansa's pioneer work, Nardini and Brebbia (1983) [16] applied the function \(1+r\) without prior knowledge of RBFs as the basis function in the Dual Reciprocity Method (DRM) in the context of the boundary element methods (BEM) to get rid of domain integral effectively. Over the years, several researchers proposed different methods which include:
- Rescaled localized radia basis function interpolation on non-cartesian and nonconforming grids [4],
- Dual Reciprocity Method (DRM) [17],
- Method of Fundamental Solutions (MFS) [18], also known as the regular BEM.
- Radial integration Method [19],
- Monte Carlo Method [20],
- Multiple reciprocity method (MRM) [21].
Table 1. Commonly used radial basis function.
| \(n\) | Type of RBF | \(\varphi(r,\epsilon)\) |
|---|---|---|
| 1 | Gaussian | \(e^{-(\epsilon^{2}r^{2})} \) |
| 2 | Wedland | \( (1-\epsilon r)^{4}+(4r+1) \) |
| 3 | Thin Plate Spline (TPS) | \( r^{3}\log(r) \) |
| 4 | Multiquadric (MQ) | \(\left(1+\epsilon^2 r^2\right)^{\frac{1}{2}}\) |
| 5 | Inverse Multiquadric (IMQ) | \(\left(1+\epsilon^2 r^2\right)^{-\frac{1}{2}}\) |
2. Radial basis interpolation
RBF interpolation method use linear combinations of \(N\) (where \(N\) is the number of data sites), radial functions \(\varphi(r)\), where \(r=||x-x_{i}||\) and \(x_{i}\) are the centers in \(\mathbb{R}^{d}\), where \(d\) is the dimension of the problem. In this section, we are considering radial basis expansion to solve a scattered data interpolation problem in \(\mathbb{R}^{d}\). It is further assumed that
The coefficients \(a_{k}\) can be obtained by activating the interpolation conditions
3. Methodology
3.1. Roles of shape parameter \((\epsilon)\)
Shape parameter \(\epsilon\) play a very important role in the determination of the shape of basis functions [3, 22, 23, 24]. It is obvious from its name (shape parameter) that if the value of \(\epsilon\) is moved over the interval \([0,\infty]\), the shape of the radial function will change effectively, (see Figure 1).Figure 1. Shapes of 1D Gaussian and IMQ RBF of different shape parameters
Theorem 1. Let \(\varphi:=\mathbb{R}^{d}\longrightarrow\mathbb{R}\) be a strictly positive definite function on \( \mathbb{R} \). Then
- \(\varphi(0)>0,\)
- \(\varphi\) is bounded, in fact \(\vert\varphi(x)\vert< \varphi(0),\forall x\in\mathbb{R}^{d}\).
Since we are considering basis functions that are strictly positive definite \((SPD)\): IMQ, Wedland and Gaussian, the Theorem 1 gives new bounds as seen in Equation (6).
Note that \( \phi(\epsilon;r) =\phi(1;\epsilon ; r)\). If we take these radial basis as \( \phi(\epsilon;r)\), as a result, the bounds explain how \( \epsilon \) would behave on the shape of the function. i.e, increment in the value of \( \epsilon \) leads to a continuous alter of the shape of the function to a spiky shape as shown in Figure 1, where the spike is denoted by \(\phi(0)\). Conversely decrements in the value of an \( \epsilon \) leads to a continuous change in the shape of the function to a flat shape, having limit at \(\phi(0)\) as well, see Figure 1 for explanation.
Earlier in this section, we mentioned the role of the shape parameter (\(\epsilon\)). Several researchers worked in this direction [1, 22, 23, 24] but only few have discussed the role of shape parameter on the accuracy and shape of the interpolant. Numerous articles and books have been dedicated to explain how vital \(\epsilon\) is to determine the shape of a radial function therefore it is obvious that the shape parameter play a vital role in the accuracy and the shape of an interpolant, therefore, the shape parameter need to be chosen wisely.
The question is: how can we choose the optimal shape parameter \(\epsilon^{*}\) with least root mean square error (\(RMSE\))? The answer of this question will be discussed later in this section.
In an attempt to determine the interval in which the optimal shape parameter exists, different algorithms have been provided by different researchers but the purpose of this research work is to provide a Trial and Error algorithm. This algorithm explain explicitly the effect of shape parameter \( \epsilon \) on the the solution of PDE problems selected for interpolation and narrows the interval in which the optimal shape parameter \(\epsilon^{*}\) is obtain. This algorithm will be discussed in Subsection 3.2.3.2. Algorithm for selecting interval of the shape parameter
The determination of best shape parameter \( \epsilon^{*} \) received attention from various researchers like [23] used trigonometric shape parameter to generalize Multiquadric RBF. Similarly, [22] showed that random variable shape parameter yield the most accurate results provided that the centers are uniformly spaced. An algorithm that determine the interval for Multiquadric shape parameter was developed in [3]. This research work, will concentrate on writing Trial and Error algorithm for choosing optimal shape parameter and its implementation on PDE problems. In [11, 27], authors described the Leave-One-Out Cross Validation and while in [28, 29], the authors introduced the Contour-Pade algorithm.It can be observed that the lower values of \(\epsilon\) result in a \((flatter)\) basis function and the higher values of \(\epsilon\) result in a \((spikier)\) basis functions and \(\epsilon=0\) result to constant basis functions. Accuracy and stability are major concerns in numerical computations. It is well known that instability increases as \(\epsilon\) decreases. The significance of this statement lies in the fact that highest accuracy is often found at some small shape parameters, which may be in an unstable region. "Trade-off principle" is the term used to denote the conflict between accuracy and numerical stability [25]. The choice of the basis function is linked with this "trade-off principle". Recently, different methods have been introduced to stably compute interpolants with small parameters by using an alternate basis, such as Contour-Pade and RBF-QR, as in [30] and [31].
Trial and Error Algorithm: To use Trial and Error algorithm, the PDE problems must be transform to matrix form i.e., \( Ab = f \), the generating data must be known [29]. If the function to be interpolate is unknown, it becomes very difficult to choose the best shape parameter. One of the easiest way to choose \((\epsilon^{*})\) is to perform a series of interpolation experiments on a large range of shape parameters then narrow it down to some selected shape parameters relative to least RMSE. Trial and Error algorithm enhances the clarification effectively on how shape parameter acts on solution of the PDE problems and gives an insight on how to narrow the interval of \( \epsilon \).
This scheme works only when the problem to be interpolated is known. We have the Algorithm 1:3.3. Root mean square error (RMSE)
DefineFrom Equation (7), the RMSE is said to be the square root of mean squared error, where \(\alpha_{j},j=1,\cdots,M\) are evaluation points and should not be mistaken for data sites; data sites errors usually disappears since we are considering an interpolant.
Due to the fact that the RMSE allows mapping of every interpolant to a single value which consequently allows comparison of results in a single way. The RMSE is in some way superior and more practically than the point-wise error.
4. Illustrative examples
In this section, the Trial and Error algorithm has been employed on some selected PDE problems in \( \mathbb{R}^{2} \) using inverse multiquadric (IMQ) RBF with evaluation points \( M = 1600 \) and with different knots \( N \) by letting \( \Omega=[0,1]^{2}\). The Root Mean Square Error is calculated by the formula given in (7).Example 1. Consider
Table 2. RMSE for Example 1 over a range of shape parameters.
| \(N\) | \(\epsilon=0.2\) | \(\epsilon=0.4\) | \(\epsilon=0.6\) | \(\epsilon=0.8\) | \(\epsilon=1.0\) | \(\epsilon=1.2\) |
|---|---|---|---|---|---|---|
| 9 | 4.947883e-03 | 7.061068e-04 | 8.306327e-03 | 1.683301e-02 | 2.501740e-02 | 3.215444e-02 |
| 25 | 1.226119e-04 | 1.233554e-04 | 2.499596e-04 | 1.163722e-03 | 2.576520e-03 | 4.351338e-03 |
| 36 | 6.759435e-06 | 1.916602e-06 | 1.024839e-05 | 1.251879e-05 | 6.232077e-05 | 1.785228e-04 |
| 289 | 7.375946e-06 | 3.628324e-06 | 1.285584e-06 | 1.239982e-05 | 2.038053e-06 | 3.000325e-05 |
| 1089 | 2.659954e-06 | 1.588367e-06 | 3.208293e-06 | 6.096696e-06 | 3.424757e-05 | 4.013821e-06 |
| 4225 | 3.605753e-05 | 6.143375e-06 | 1.669543e-06 | 5.970569e-06 | 2.033888e-05 | 7.354744e-05 |
Figure 2. Error Comparison for Example 1
Figure 3. Interpolant for Example 1 and its corresponding data sites
Example 2. Consider
Table 3. RMSE for Example 2 over a range of shape parameter \((\epsilon)\).
| \(N\) | \(\epsilon=1.0\) | \(\epsilon=1.2 \) | \(\epsilon=1.4\) | \(\epsilon=1.6\) | \(\epsilon=1.8\) | \(\epsilon=2.0\) |
|---|---|---|---|---|---|---|
| 9 | 5.361079e-02 | 6.657915e-02 | 7.686519e-02 | 8.599953e-02 | 9.281620e-02 | 9.719250e-02 |
| 25 | 7.972262e-03 | 1.192263e-02 | 1.633815e-02 | 2.100864e-02 | 2.578031e-02 | 3.055183e-02 |
| 36 | 2.857109e-04 | 6.473231e-04 | 1.210261e-03 | 1.977596e-03 | 2.933024e-03 | 4.050198e-03 |
| 289 | 1.659403e-06 | 4.254667e-06 | 9.665239e-06 | 2.699984e-05 | 5.940062e-05 | 1.145354e-04 |
| 1089 | 1.6725029e-06 | 3.219273e-06 | 1.395574e-05 | 1.838989e-06 | 1.024784e-06 | 4.224696e-07 |
| 4225 | 2.991273e-05 | 3.095514e-05 | 6.726647e-06 | 6.386367e-06 | 3.699115e-06 | 8.021659e-06 |
Figure 4. Error Comparison for Example 2
Figure 5. The approximate solution for Example 2 and its corresponding RMSE for different \(n\)
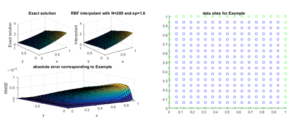
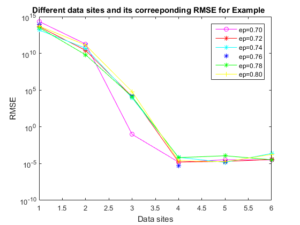
Example 3. Consider a second order PDE [32] \begin{equation*} \dfrac{\partial^{2}u}{\partial x\partial y}=4x+e^{x}, ~~~ (x,y)\in [0,1]\times[0,1] \end{equation*} with supplementary conditions \(\dfrac{\partial u(0,y)}{\partial y}= y,~~y\in[0,1], \) and \( u(x,0)= 2, ~~ x\in [0,1].\) The exact solution of this problem is \( u(x,y)=2x^{2}y+ye^{x}+\frac{y^{2}}{2}-y+2. \) Table 3 presents the RMSE for different data sites which correspond to Figure 6. The shape parameter that best fits the problem is tabulated in Table 6 and its corresponding figure is shown in Figure 7.
Table 4. RMSE for Equation 3 over a range of shape parameters \((\epsilon)\).
| \(N\) | \(\epsilon=0.70\) | \(\epsilon=0.72\) | \(\epsilon=0.74\) | \(\epsilon=0.76\) | \(\epsilon=0.78\) | \(\epsilon=0.80\) |
|---|---|---|---|---|---|---|
| 9 | 2.158636e+14 | 4.409283e+13 | 1.506239e+13 | 8.352088e+13 | 3.278437e+ | 5.099321e+ |
| 25 | 1.890692e+11 | 2.546641e+10 | 4.975475e+10 | 1.338177e+11 | 1.278434e+0014 | 1.367660e+11 |
| 36 | 9.573340e+02 | 1.349606e+04 | 8.731797e+03 | 1.758439e+04 | 1.274839e+04 | 6.150933e+04 |
| 289 | 1.606563e-05 | 1.632955e-05 | 7.146346e-05 | 4.759347e-06 | 6.556112e-05 | 2.439145e-05 |
| 1089 | 3.359890e-05 | 1.951918e-05 | 1.472573e-05 | 1.544620e-05 | 1.163340e-04 | 1.796294e-05 |
| 4225 | 3.174857e-05 | 3.725997e-05 | 2.397563e-04 | 2.986440e-05 | 3.321418e-05 | 1.772710e-04 |
Figure 6. Error Comparison for Example 3
Figure 7. Interpolant for Example 3 and its corresponding data sites
Example 4.
Consider PDE with variable coefficient: \begin{equation*} \begin{cases} (2-x^{2}-y^{2})\dfrac{\partial^{2}u}{\partial x^{2}}+\exp(x-y)\dfrac{\partial^{2}u}{\partial y^{2}}+2x\dfrac{\partial u}{\partial x}-\exp(x-y)\dfrac{\partial u}{\partial y}\\ =32y(1-y)(3x^{2}+y^{2}-x-2)-16x(1-x)(3-2y)\exp(x-y),~(x,y)\in[-1,1]^2 \end{cases} \end{equation*} with boundary conditions \(u(x,0)=u(x,1)=u(0,y)=u(1,y).\) The exact solution is \(u(x,y)=16x(1-x)y(1-y). \)
Table 4 presents the RMSE for different data sites which correspond to Figure 9. The shape parameter that best fits the problem is tabulated in Table 6 and its corresponding figure is shown in Figure 8.Table 5. RMSE for Example 4 over a range of shape parameter \((\epsilon)\)
| Data sites | Example 1 \(\epsilon^{*}=0.4 \) | Example 2 \(\epsilon^{*}=1.6 \) | Example 3 \(\epsilon^{*}=0.72 \) | Example 4 \(\epsilon^{*}=2.4\) |
|---|---|---|---|---|
| 9 | 7.061068e-04 | 8.599953e-02 | 4.409283e+13 | 3.417120e-01 |
| 25 | 1.233554e-04 | 2.100864e-02 | 2.546641e+10 | 8.421439e-02 |
| 81 | 1.916602e-06 | 1.977596e-03 | 1.349606e+04 | 1.434081e-02 |
| 289 | 3.628324e-06 | 2.620360e-05 | 1.632955e-05 | 7.800962e-04 |
| 1089 | 1.588367e-06 | 2.699984e-06 | 1.951918e-05 | 3.327200e-06 |
| 4225 | 6.143375e-06 | 6.386367e-06 | 3.725997e-05 | 9.814452e-06 |
Figure 8. Error Comparison for Example 4
Figure 9. Interpolant for Example 4 and its corresponding data sites
Table 6. RMSE for the examples considered with their respective optimal shape parameter \((\epsilon^{*})\).
| Data sites | Example 1 \(\epsilon^{*}=0.4 \) | Example 2 \(\epsilon^{*}=1.6 \) | Example 3 \(\epsilon^{*}=0.72 \) | Example 4 \(\epsilon^{*}=2.4\) |
|---|---|---|---|---|
| 9 | 7.061068e-04 | 8.599953e-02 | 4.409283e+13 | 3.417120e-01 |
| 25 | 1.233554e-04 | 2.100864e-02 | 2.546641e+10 | 8.421439e-02 |
| 81 | 1.916602e-06 | 1.977596e-03 | 1.349606e+04 | 1.434081e-02 |
| 289 | 3.628324e-06 | 2.620360e-05 | 1.632955e-05 | 7.800962e-04 |
| 1089 | 1.588367e-06 | 2.699984e-06 | 1.951918e-05 | 3.327200e-06 |
| 4225 | 6.143375e-06 | 6.386367e-06 | 3.725997e-05 | 9.814452e-06 |
5. Discussion of results and conclusion
5.1. Discussion of Results
Tables 2-5 are the product of the errors obtained from interpolating Examples 1-4. Table 6 summarizes all the RMSE for the examples considered with their respective best shape parameters. The data sites used in this research work are \(N = [9,25,81,289,1089,4225]\) (gotten from \(\left(2^k+1\right)^d,~k=1,~2,\ldots\)). It is visually obvious from the tables that the errors follow a pattern irrespective of the examples (that's the errors decline as the data sites increases) as shown in Table 6. In Example 3, it can be noticed that with small data sites; \([9,~25,~81]\) (that is \(\left(2^k+1\right)^d,~k=1,~2,~3\) and \(d=2\)) the RMSE are very bad, irrespective of the choice of shape parameter, but as the data sites increases (that is, \(\left(2^k+1\right)^d,~k=4,~5,\ldots\) and \(d=2\)) the RMSE improves. In fact, the best shape parameter exists at \( (\epsilon^{*}=0.72) \).5.2. Conclusion
In this research work, Trial and Error scheme is proposed to determine the range in which the best shape parameter \( \epsilon^{*} \) lies via IMQ radial function by performing interpolation experiments and selecting which experiment produces the least RMSE for different data sites. We have illustrated the formulation and implementation of this process on some selected PDE problems. Obviously, numerical results demonstrated that the scheme alongside the Matlab codes has immensely reduced time and ease the complexity involved in the computation, thus, making this scheme an effective and efficient technique for solving partial differential equations.Acknowledgments
The authors wishes to express his profound gratitude to the reviewers for their useful comments on the manuscript.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflict of Interests
The authors declare no conflict of interest.References
- Larsson, E., Lehto, E., Heryudono, A. & Fornberg, B. (2013). Stable computation of differentiation matrices and scattered node stencils based on Gaussian radial basis functions. SIAM Journal on Scientific Computing, 35(4), A2096-A2119.[Google Scholor]
- Hardy, R. L. (1971). Multiquadric equations of topography and other irregular surfaces. Journal of geophysical research, 76(8), 1905-1915.[Google Scholor]
- Biazar, J. & Hosami, M. (2016). Selection of an interval for variable shape parameter in approximation by radial basis functions. Advances in Numerical Analysis, 2016.[Google Scholor]
- Deparis, S., Forti, D. & Quarteroni, A. (2014). A rescaled localized radial basis function interpolation on non-Cartesian and nonconforming grids. SIAM Journal on Scientific Computing, 36(6), A2745-A2762.[Google Scholor]
- Fedoseyev, A. I., Friedman, M. J. & Kansa, E. J. (2002). Improved multiquadric method for elliptic partial differential equations via PDE collocation on the boundary. Computers & Mathematics with Applications, 43(3-5), 439-455.[Google Scholor]
- Sarra, S. A. & Kansa, E. J. (2009). Multiquadric radial basis function approximation methods for the numerical solution of partial differential equations. Advances in Computational Mechanics, 2(2).[Google Scholor]
- Dehghan, M. & Shokri, A. (2009). Numerical solution of the nonlinear Klein–Gordon equation using radial basis functions. Journal of Computational and Applied Mathematics, 230(2), 400-410.[Google Scholor]
- Iske, A. (2002). Scattered data modelling using radial basis functions. In Tutorials on Multiresolution in Geometric Modelling (pp. 205-242). Springer, Berlin, Heidelberg.[Google Scholor]
- Kansa, E. J. & Carlson, R. E. (1992). Improved accuracy of multiquadric interpolation using variable shape parameters. Computers & Mathematics with Applications, 24(12), 99-120.[Google Scholor]
- Hardy, R. L. (1990). Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968–1988. Computers & Mathematics with Applications, 19(8-9), 163-208.[Google Scholor]
- Franke, R. (1982). Scattered data interpolation: tests of some methods. Mathematics of computation, 38(157), 181-200.[Google Scholor]
- Duchon, J. (1977). Splines minimizing rotation-invariant semi-norms in Sobolev spaces. In Constructive theory of functions of several variables (pp. 85-100). Springer, Berlin, Heidelberg.[Google Scholor]
- Micchelli, C. A. (1984). Interpolation of scattered data: distance matrices and conditionally positive definite functions. In Approximation theory and spline functions (pp. 143-145). Springer, Dordrecht.[Google Scholor]
- Kansa, E. J. (1990). Multiquadrics--A scattered data approximation scheme with applications to computational fluid--dynamics--I surface approximations and partial derivative estimates. Computers & Mathematics with applications, 19(8--9), 127--145.[Google Scholor]
- Kansa, E. J. (1990). Multiquadrics--A scattered data approximation scheme with applications to computational fluid--dynamics--II solutions to parabolic, hyperbolic and elliptic partial differential equations. Computers & mathematics with applications, 19(8--9), 147--161.[Google Scholor]
- Nardini, D. & Brebbia, C. A. (1983). A new approach to free vibration analysis using boundary elements. Applied mathematical modelling, 7(3), 157-162.[Google Scholor]
- Partridge, P. W. & Brebbia, C. A. (Eds.). (2012). Dual reciprocity boundary element method. Springer Science & Business Media.[Google Scholor]
- Kupradze, V. D. & Aleksidze, M. A. (1964). The method of functional equations for the approximate solution of certain boundary value problems. USSR Computational Mathematics and Mathematical Physics, 4(4), 82-126.[Google Scholor]
- Gao, X. W. (2006). A meshless BEM for isotropic heat conduction problems with heat generation and spatially varying conductivity. International journal for numerical methods in engineering, 66(9), 1411-1431.[Google Scholor]
- Chen, C. S., Golberg, M. A. & Hon, Y. C. (1998). The method of fundamental solutions and quasi-Monte-Carlo method for diffusion equations. International Journal for Numerical Methods in Engineering, 43(8), 1421-1435.[Google Scholor]
- Nowak, A. J. & Partridge, P. W. (1992). Comparison of the dual reciprocity and the multiple reciprocity methods. Engineering analysis with boundary elements, 10(2), 155-160.[Google Scholor]
- Sarra, S. A. & Sturgill, D. (2009). A random variable shape parameter strategy for radial basis function approximation methods. Engineering Analysis with Boundary Elements, 33(11), 1239-1245.[Google Scholor]
- Xiang, S., Wang, K. M., Ai, Y. T., Sha, Y. D. & Shi, H. (2012). Trigonometric variable shape parameter and exponent strategy for generalized multiquadric radial basis function approximation. Applied Mathematical Modelling, 36(5), 1931-1938.[Google Scholor]
- Mongillo, M. (2011). Choosing basis functions and shape parameters for radial basis function methods. SIAM undergraduate research online, 4(190-209), 2-6.[Google Scholor]
- Fasshauer, G. E. (2007). Meshfree approximation methods with MATLAB(Vol. 6). World Scientific.[Google Scholor]
- Wilkins, M. F., Boddy, L., Morris, C. W. & Jonker, R. (1996). A comparison of some neural and non-neural methods for identification of phytoplankton from flow cytomery data. Bioinformatics, 12(1), 9-18.[Google Scholor]
- Rippa, S. (1999). An algorithm for selecting a good value for the parameter c in radial basis function interpolation. Advances in Computational Mathematics, 11(2-3), 193-210.[Google Scholor]
- Wright, G. B. (2003). Radial basis function interpolation: numerical and analytical developments.[Google Scholor]
- Wright, G. B. & Fornberg, B. (2006). Scattered node compact finite difference-type formulas generated from radial basis functions. Journal of Computational Physics, 212(1), 99-123.[Google Scholor]
- Fornberg, B. & Wright, G. (2004). Stable computation of multiquadric interpolants for all values of the shape parameter. Computers & Mathematics with Applications, 48(5-6), 853-867.[Google Scholor]
- Piret, C. (2007). Analytical and numerical advances in radial basis functions. Ph. D. thesis. [Google Scholor]
- Ngai, S. C. (2004). Numerical Solution of Partial Differential Equations with the Tau-Collocation Method. City University of Hong Kong.[Google Scholor]