Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2020.0113
Valuations and their generalizations for UP-algebras
Siriwan Pawai, Tararat Khamsang, Aiyared Iampan\(^1\)
Department of Mathematics, School of Science, University of Phayao, Phayao 56000, Thailand.; (S.P & T.K & A.I)
\(^{1}\)Corresponding Author: aiyared.ia@up.ac.th
Abstract
Keywords:
1. Introduction
The fundamental concept of pseudo-valuation was first introduced by Busne¸ag [1] in 1996. He defined a pseudo-valuation on a Hilbert algebra and proved that every pseudo-valuation induces a pseudo metric on a Hilbert algebra. In 2003, Buşneag [2] provided several theorems on extensions of pseudo-valuations. In 2007, Buşneag [3] introduced the notion of a pseudo-valuation (valuations) on a residuated lattice and proved some theorems of extension for these (using the model of a Hilbert algebra).
In 2010, Doh and Kang [4] introduced the notion of a pseudo-valuation on a BCK/BCI-algebra and studied results based on a pseudo-valuation. Ghorbani [5] defined a congruence relation and gave a quotient structure of a BCI-algebra based on a pseudo-valuation. In 2011, Doh and Kang [6] introduced the notion of a commutative pseudo valuation on a BCK-algebra. Jun et al., [7] introduced the notion of a positive implicative pseudo-valuation on a BCK-algebra and investigated its characterizations. In 2012, Jun et al., [8] introduced the notions of a pseudo-valuation and a valuation on a BCC-algebra. In 2013, Zhan and Jun [9] introduced the notions of a pseudo-valuation and an implicative pseudo-valuation on a \(R_{0}\)-algebra. Lee [10] introduced the notions of a pseudo-valuation and a valuation, and a pseudo-metric is induced by a pseudo-valuation on a BE-algebra. In 2015, Song et al., [11] introduced the notions of a quasi-valuation map based on a subalgebra and an ideal on a BCK/BCI-algebra. In 2017, Yang and Xin [12] introduced the notions of a pseudo pre-valuation, an implicative pseudo pre-valuation, a positive implicative pseudo pre-valuation, and a strong pseudo pre-valuation, and investigated some characterizations of an EQ-algebra. In 2018, Mehrshada and Kouhestanib [13] studied some properties of a pseudo-valuation and their induced metrics on a BCK-algebra and showed that there are many pseudo-valuations on a BCK-algebra.
In 2019, Koam et al., [14] introduced the notion of a pseudo-metric which induced from a pseudo-valuation on a KU-algebra. Ali et al., [15] introduced the notion of a pseudo-valuation and investigated the relationship between a pseudo-valuation and an ideal of a JU-algebra. Romano [16] introduced the notion of a pseudo-valuation on a UP-algebra and analyzed the relationship of these mappings with UP-substructures.
In this paper, we introduce the notions of a weak pseudo-valuation, a \(0\)-weak pseudo-valuation, a weak valuation, a near pseudo-valuation, a near valuation, a pseudo-valuation, and a valuation and induce a pseudo-metric without triangle inequality, a quasi pseudo-metric, a pseudo-metric, and a metric by some these mappings on a UP-algebra. We also prove that the binary operation defined on a UP-algebra is uniformly continuous under the induced metric by a valuation in some conditions.
Before we begin our study, we will give the definition of UP-algebras.
Definition 1. [17] An algebra \(A=(A,\cdot,0)\) of type \((2,0)\) is called a UP-algebra, where \(A\) is a nonempty set, \(\cdot\) is a binary operation on \(A\), and \(0\) is a fixed element of \(A\) (i.e., a nullary operation) if it satisfies the following axioms:
- (UP-1) \((\forall x,y,z\in A)((y\cdot z)\cdot((x\cdot y)\cdot(x\cdot z))=0)\),
- (UP-2) \((\forall x\in A)(0\cdot x=x)\),
- (UP-3) \((\forall x\in A)(x\cdot0=0)\), and
- (UP-4) \((\forall x,y\in A)(x\cdot y=0,y\cdot x=0\Rightarrow x=y)\).
Example 1.[19] Let \(X\) be a universal set and let \(\Omega\in\mathcal{P}(X)\) where \(\mathcal{P}(X)\) means the power set of \(X\). Let \(\mathcal{P}_{\Omega}(X)=\{A\in\mathcal{P}(X)\mid\Omega\subseteq A\}\). Define a binary operation \(\cdot\) on \(\mathcal{P}_{\Omega}(X)\) by putting \(A\cdot B=B\cap (A^{C}\cup\Omega)\) for all \(A,B\in\mathcal{P}_{\Omega}(X)\) where \(A^{C}\) means the complement of a subset \(A\). Then \((\mathcal{P}_{\Omega}(X),\cdot,\Omega)\) is a UP-algebra and we shall call it the generalized power UP-algebra of type 1 with respect to \(\Omega\). Let \(\mathcal{P}^{\Omega}(X)=\{A\in\mathcal{P}(X)\mid A\subseteq\Omega\}\). Define a binary operation \(\ast\) on \(\mathcal{P}^{\Omega}(X)\) by putting \(A\ast B=B\cup (A^{C}\cap\Omega)\) for all \(A,B\in\mathcal{P}^{\Omega}(X)\). Then \((\mathcal{P}^{\Omega}(X),\ast,\Omega)\) is a UP-algebra and we shall call it the generalized power UP-algebra of type 2 with respect to \(\Omega\). In particular, \((\mathcal{P}(X),\cdot,\emptyset)\) is a UP-algebra and we shall call it the power UP-algebra of type 1, and \((\mathcal{P}(X),\ast,X)\) is a UP-algebra and we shall call it the power UP-algebra of type 2.
Example 2.[20] Let \(\mathbb {N}_{0}\) be the set of all natural numbers with zero. Define two binary operations \(\circ\) and \(\bullet\) on \(\mathbb{N}_{0}\) by \begin{align*} (\forall x,y\in\mathbb{N}_{0})\left(x\circ y = \left\{ \begin{array}{ll} y & \text{if}~x< y, \\ 0 & \text{otherwise} \end{array} \right.\right) \end{align*} and \begin{align*} (\forall x,y\in\mathbb{N}_{0})\left( x\bullet y = \left\{ \begin{array}{ll} y & \text{if}~x>y~\text{or}~x=0, \\ 0 & \text{otherwise} \end{array} \right.\right). \end{align*} Then \((\mathbb{N}_{0},\circ,0)\) and \((\mathbb{N}_{0},\bullet,0)\) are UP-algebras.
Example 3.[21] Let \(A=\{0,1,2,3,4\}\) be a set with a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*}\label{eqMEX012} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 4 \\ 2 & 0 & 1 & 0 & 0 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \\ \end{array} \end{equation*} Then \((A,\cdot,0)\) is a UP-algebra.
For more examples of UP-algebras, see [19,22,23,24,25].In a UP-algebra \(A=(A,\cdot,0)\), the following assertions are valid (see [17,24]).
\begin{align} &\label{UP2_1} (\forall x\in A)(x\cdot x=0), \\ &\label{UP2_13} (\forall x,y,z\in A)(x\cdot y=0, y\cdot z=0 \Rightarrow x\cdot z=0), \\ &\label{UP2_6} (\forall x,y,z\in A)(x\cdot y=0 \Rightarrow (z\cdot x)\cdot (z\cdot y)=0), \\ &\label{UP2_7} (\forall x,y,z\in A)(x\cdot y=0 \Rightarrow (y\cdot z)\cdot (x\cdot z)=0), \\ &\label{UP2_14} (\forall x,y\in A)(x\cdot (y\cdot x)=0), \\ &\label{UP2_16} (\forall x,y\in A)((y\cdot x)\cdot x=0 \Leftrightarrow x=y\cdot x), \\ &\label{UP2_15} (\forall x,y\in A)(x\cdot (y\cdot y)=0), \\ &\label{UP2_add1} (\forall a,x,y,z\in A)((x\cdot(y\cdot z))\cdot(x\cdot((a\cdot y)\cdot (a\cdot z)))=0), \end{align} \begin{align} &\label{UP2_add2} (\forall a,x,y,z\in A)((((a\cdot x)\cdot (a\cdot y))\cdot z)\cdot((x\cdot y)\cdot z)=0), \\ &\label{UP2_add3} (\forall x,y,z\in A)(((x\cdot y)\cdot z)\cdot(y\cdot z)=0), \\ &\label{UP2_add4} (\forall x,y,z\in A)(x\cdot y=0 \Rightarrow x\cdot (z\cdot y)=0), \\ &\label{UP2_add5} (\forall x,y,z\in A)(((x\cdot y)\cdot z)\cdot(x\cdot(y\cdot z))=0),\, \text{and} \\ &\label{UP2_add6} (\forall a,x,y,z\in A)(((x\cdot y)\cdot z)\cdot(y\cdot(a\cdot z))=0). \end{align} From [17], the binary relation \(\leq\) on a UP-algebra \(A=(A,\cdot,0)\) is defined as follows:Definition 2. [17,26,27,28] A nonempty subset \(S\) of a UP-algebra \(A=(A,\cdot,0)\) is called
- (1) a UP-subalgebra of \(A\) if \((\forall x,y\in S)(x\cdot y\in S)\).
- (2) a near UP-filter of \(A\) if it satisfies the following conditions:
- (i) the constant \(0\) of \(A\) is in \(S\), and
- (ii) \((\forall x,y\in A)(y\in S\Rightarrow x\cdot y\in S)\).
- (3) a UP-filter of \(A\) if it satisfies the following conditions:
- (i) the constant \(0\) of \(A\) is in \(S\), and
- (ii) \((\forall x,y\in A)(x\cdot y\in S,x\in S\Rightarrow y\in S)\).
- (4) a UP-ideal of \(A\) if it satisfies the following conditions:
- (i) the constant \(0\) of \(A\) is in \(S\), and
- (ii) \((\forall x,y,z\in A)(x\cdot(y\cdot z)\in S,y\in S\Rightarrow x\cdot z\in S)\).
- (5) a strong UP-ideal (renamed from a strongly UP-ideal) of \(A\) if it satisfies the following conditions:
- (i) the constant \(0\) of \(A\) is in \(S\), and
- (ii) \((\forall x,y,z\in A)((z\cdot y)\cdot(z\cdot x)\in S,y\in S\Rightarrow x\in S)\).
Iampan [26,27] proved that the notion of UP-subalgebras is a generalization of near UP-filters, near UP-filters is a generalization of UP-filters, UP-filters is a generalization of UP-ideals, and UP-ideals is a generalization of strong UP-ideals. Furthermore, they proved that the only strong UP-ideal of a UP-algebra \(A\) is \(A\).
2. Valuations and their generalizations
In this section, we introduce the notions of a weak pseudo-valuation, a \(0\)-weak pseudo-valuation, a weak valuation, a near pseudo-valuation, a near valuation, a pseudo-valuation, and a valuation on a UP-algebra. From now on, unless another thing is stated, we take \(A=(A,\cdot,0)\) as a UP-algebra.
Definition 3. A real-valued function \(\varphi\) on \(A\) is called a pseudo-valuation on \(A\) if it satisfies the following conditions: \begin{align} \label{K2A01_1} &\varphi(0)=0, \\ \label{K2A01_2} &(\forall x,y\in A)(\varphi(y)\leq\varphi(x\cdot y)+\varphi(x)). \end{align} A pseudo-valuation \(\varphi\) on \(A\) is called a valuation on \(A\) if it satisfies the following condition:
Definition 4. A real-valued function \(\varphi\) on \(A\) is called a near pseudo-valuation on \(A\) if it satisfies the condition (15) and the following condition:
Definition 5. A real-valued function \(\varphi\) on \(A\) is called a weak pseudo-valuation on \(A\) if
Theorem 1. Every nonnegative constant real-valued function on \(A\) is a weak pseudo-valuation.
Proof. Let \(\varphi\) be a nonzero constant real-valued function on \(A\). Then there exists a nonnegative real number \(c\) such that \(\varphi(x)=c\) for all \(x \in A\). Let \(x,y\in A\). Then \begin{align*} \varphi(x\cdot y)=c \leq c+c=\varphi(x)+\varphi(y). \end{align*} Hence, \(\varphi\) is a weak pseudo-valuation on \(A\).
The following example shows that the converse of Theorem 1 is not true in general.Example 4. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 3 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 4 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0.2} \,\,\, {1\atop 0.6} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.5} \,\,\, {4\atop 0.2} \right). \end{equation*}
Then \(\varphi\) is a weak pseudo-valuation on \(A\). But \(\varphi\) is not a nonnegative constant real-valued function on \(A\) because \(\varphi(0)=0.2\neq0.6= \varphi(1)\).
Theorem 2. The zero constant real-valued function on \(A\) is a \(0\)-weak pseudo-valuation (resp., near pseudo-valuation, pseudo-valuation).
Proof. It is straightforward from the definitions of \(0\)-weak pseudo-valuations, near pseudo-valuations, and pseudo-valuations.
If \(A\) has more than one element, then the zero constant real-valued function on \(A\) is not a weak valuation, a near valuation, and a valuation.
The following example shows that the converse of Theorem 2 is not true in general.
Example 5. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 0 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0.4} \,\,\, {3\atop 0.7} \,\,\, {4\atop 0.1} \right). \end{equation*}
Then \(\varphi\) is a pseudo-valuation on \(A\). But \(\varphi\) is not a zero constant real-valued function on \(A\) because \(\varphi(0)=0\neq0.5=\varphi(1)\).
Example 6. From Example 2, we have \((\mathbb{N}_{0},\circ,0)\) is a UP-algebra. Let \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(0)=0\) and if \(x\leq y\) where \(\leq\) is the standard ordering among real numbers, then \(0< \varphi(x)\leq\varphi(y)\) for all positive numbers \(x, y\). Let \(x, y\in\mathbb{N}_{0}\).
- Case 1: \(x< y\). Then \(\varphi(x\circ y)=\varphi(y)\). Thus \(\varphi(x\circ y)+\varphi(x)=\varphi(y)+\varphi(x)\geq\varphi(y)\).
- Case 2: \(x\geq y\). Then \(\varphi(x\circ y)=\varphi(0)=0\). Thus \(\varphi(x\circ y)+\varphi(x)=0+\varphi(x)=\varphi(x)\). If \(y=0\), then \(\varphi(y)=0\). Thus \(\varphi(x\circ y)+\varphi(x)=\varphi(x)\geq 0=\varphi(y)\). If \(x=0\), then \(y=0\). By the above proof, we have \(\varphi(x\circ y)+\varphi(x)=\varphi(x)\geq 0=\varphi(y)\). If \(x>0\) and \(y>0\), it follows from the definition of \(\varphi\) that \(\varphi(x\circ y)+\varphi(x)=\varphi(x)\geq\varphi(y)\).
Hence, \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 7. From Example 2, we have \((\mathbb{N}_{0},\circ,0)\) is a UP-algebra. Let \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(x)=x\) for all \(x\in\mathbb{N}_{0}\). By Example 6, we have \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 8. From Example 2, we have \((\mathbb{N}_{0},\bullet,0)\) is a UP-algebra. Let \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(0)=0\) and if \(x\leq y\) where \(\leq\) is the standard ordering among real numbers, then \(\varphi(x)\geq\varphi(y)>0\) for all positive numbers \(x, y\). Let \(x, y\in\mathbb{N}_{0}\).
- Case 1: \(x>y\) or \(x=0\). Then \(\varphi(x\bullet y)=\varphi(y)\). Thus \(\varphi(x\bullet y)+\varphi(x)=\varphi(y)+\varphi(x)\geq\varphi(y)\).
- Case 2: \(x\leq y\) and \(x\neq 0\). Then \(y\neq 0\) and \(\varphi(x\bullet y)=\varphi(0)=0\). Since \(x>0\) and \(y>0\), it follows from the definition of \(\varphi\) that \(\varphi(x\bullet y)+\varphi(x)=0+\varphi(x)=\varphi(x)\geq\varphi(y)\).
Hence, \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 9. From Example 2, we have \((\mathbb{N}_{0},\bullet,0)\) is a UP-algebra. Let \(c\) be a positive real number and \(\varphi\) be a real-valued function on \(\mathbb{N}_{0}\) defined by \(\varphi(0)=0\) and \(\varphi(x)=c\) for all positive number \(x\). By Example 8, we have \(\varphi\) is a valuation on \(\mathbb{N}_{0}\).
Example 10. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 3 & 0 & 1 & 2 & 0 & 0 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.2} \right). \end{equation*}
Then \(\varphi\) is a valuation on \(A\).
Example 11. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.5} \right). \end{equation*}
Then \(\varphi\) is a pseudo-valuation on \(A\).
Example 12. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 3 \\ 2 & 0 & 0 & 0 & 3 & 3 \\ 3 & 0 & 1 & 1 & 0 & 1 \\ 4 & 0 & 0 & 1 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.3} \,\,\, {2\atop 0.9} \,\,\, {3\atop 0.2} \,\,\, {4\atop 0.5} \right). \end{equation*}
Then \(\varphi\) is a near pseudo-valuation on \(A\).
Example 13. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 2 \\ 2 & 0 & 0 & 0 & 0 & 2 \\ 3 & 0 & 0 & 1 & 0 & 2 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0.4} \,\,\, {3\atop 0.7} \,\,\, {4\atop 0.1} \right). \end{equation*}
Then \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\).
Example 14. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 0 & 0 & 4 \\ 4 & 0 & 4 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0.2} \,\,\, {1\atop 0.4} \,\,\, {2\atop 0.9} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.1} \right). \end{equation*}
Then \(\varphi\) is a weak pseudo-valuation on \(A\).
Example 15. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 4 & 0 \\ 3 & 0 & 1 & 0 & 0 & 0 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.3} \,\,\, {3\atop 0.8} \,\,\, {4\atop 0.4} \right). \end{equation*}
Then \(\varphi\) is a near valuation on \(A\).
Example 16. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 2 \\ 2 & 0 & 0 & 0 & 3 & 2 \\ 3 & 0 & 1 & 1 & 0 & 2 \\ 4 & 0 & 0 & 0 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.2} \,\,\, {4\atop 0.5} \right). \end{equation*}
Then \(\varphi\) is a weak valuation on \(A\).
Theorem 3. Every near pseudo-valuation \(\varphi\) on \(A\) satisfies the following condition:
Proof. Let \(x\in A\). Then \( 0 =\varphi(0) =\varphi(x\cdot x) \leq\varphi(x). \)
Theorem 4. Every valuation on \(A\) is a pseudo-valuation.
Proof. It is straightforward from the definitions of valuations and pseudo-valuations.
Theorem 5. Every pseudo-valuation on \(A\) is a near pseudo-valuation.
Proof. Let \(\varphi\) be a pseudo-valuation on \(A\). Let \(x,y\in A\). Then \( \varphi(x\cdot y) \leq\varphi(y\cdot(x\cdot y))+\varphi(y) =\varphi(0)+\varphi(y) =0+\varphi(y) =\varphi(y). \) Hence, \(\varphi\) is a near pseudo-valuation on \(A\).
Theorem 6. Every near pseudo-valuation on \(A\) is a \(0\)-weak pseudo-valuation.
Proof. Let \(\varphi\) be a near pseudo-valuation on \(A\). Clearly, \(\varphi(0)=0\). Let \(x,y\in A\). Then \(\varphi(x\cdot y) \leq\varphi(y)\leq\varphi(x)+\varphi(y). \) Hence, \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\).
Theorem 7. Every \(0\)-weak pseudo-valuation on \(A\) is a weak pseudo-valuation.
Proof. It is straightforward from the definitions of \(0\)-weak pseudo-valuations and weak pseudo-valuations.
Theorem 8. Every valuation on \(A\) is a near valuation.
Proof. It is straightforward from the definitions of valuations and near valuations and Theorem 5.
Theorem 9. Every near valuation on \(A\) is a weak valuation.
Proof. It is straightforward from the definitions of near valuations and weak valuations and Theorem 6.
Theorem 10. Every weak valuation on \(A\) is a \(0\)-weak pseudo-valuation.
Proof. It is straightforward from the definitions of weak valuations and \(0\)-weak pseudo-valuations.
Theorem 11. Every near valuation on \(A\) is a near pseudo-valuation.
Proof. It is straightforward from the definitions of near valuations and near pseudo-valuations.
The following example shows that the converse of Theorem 4 is not true in general.Example 17. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.5} \,\,\, {2\atop 0} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.2} \right). \end{equation*} Then \(\varphi\) is a pseudo-valuation on \(A\). But \(\varphi\) is not a valuation on \(A\) because there exists \(2\neq0\) and \(\varphi(2)=0\).
The following example shows that the converse of Theorem 5 is not true in general.Example 18. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 1 & 3 & 3 \\ 2 & 0 & 0 & 0 & 3 & 3 \\ 3 & 0 & 0 & 1 & 0 & 1 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.5} \,\,\, {3\atop 0.1} \,\,\, {4\atop 0.4} \right). \end{equation*} Then \(\varphi\) is a near pseudo-valuation on \(A\). But \(\varphi\) is not a pseudo-valuation on \(A\) because \(\varphi(1)=0.2\nleq0.1=0+0.1=\varphi(0)+\varphi(3)=\varphi(3\cdot1)+\varphi(3)\).
The following example shows that the converse of Theorem 6 is not true in general.Example 19. From Example 13, let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.1} \,\,\, {2\atop 0.2} \,\,\, {3\atop 0.5} \,\,\, {4\atop 0.1} \right). \end{equation*} Then \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\). But \(\varphi\) is not a near pseudo-valuation on \(A\) as \(\varphi(1\cdot4)=\varphi(2)=0.2\nleq0.1=\varphi(4)\).
The following example shows that the converse of Theorem 7 is not true in general.Example 20. From Example 14, let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0.2} \,\,\, {1\atop 0.1} \,\,\, {2\atop 0.4} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.1} \right). \end{equation*} Then \(\varphi\) is a weak pseudo-valuation on \(A\). But \(\varphi\) is not a \(0\)-weak pseudo-valuation on \(A\) because \(\varphi(0)=0.2\).
The following example shows that the converse of Theorem 8 is not true in general.Example 21. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 4 & 0 \\ 3 & 0 & 1 & 2 & 0 & 0 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.7} \,\,\, {3\atop 0.9} \,\,\, {4\atop 0.5} \right). \end{equation*} Then \(\varphi\) is a near valuation on \(A\). But \(\varphi\) is not a valuation on \(A\) because \(\varphi(4)=0.5\nleq0.2=0+0.2=\varphi(0)+\varphi(1)=\varphi(1\cdot4)+\varphi(1)\).
The following example shows that the converse of Theorem 9 is not true in general.Example 22. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 0 & 0 & 0 & 2 \\ 3 & 0 & 1 & 1 & 0 & 2 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.2} \,\,\, {2\atop 0.5} \,\,\, {3\atop 0.2} \,\,\, {4\atop 0.3} \right). \end{equation*} Then \(\varphi\) is a weak valuation on \(A\). But \(\varphi\) is not a near valuation on \(A\) because \(\varphi(2\cdot4)=\varphi(2)=0.5\nleq0.3=\varphi(4)\).
The following example shows that the converse of Theorem 10 is not true in general.Example 23. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 4 \\ 2 & 0 & 0 & 0 & 0 & 1 \\ 3 & 0 & 1 & 1 & 0 & 1 \\ 4 & 0 & 0 & 0 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.10} \,\,\, {2\atop 0.45} \,\,\, {3\atop 0.75} \,\,\, {4\atop 0} \right). \end{equation*} Then \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\). But \(\varphi\) is not a weak valuation on \(A\) because \(\varphi(4)=0\).
The following example shows that the converse of Theorem 11 is not true in general.Example 24. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 0 & 0 \\ 3 & 0 & 1 & 2 & 0 & 0 \\ 4 & 0 & 1 & 2 & 4 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.7} \,\,\, {2\atop 0.9} \,\,\, {3\atop 0.1} \,\,\, {4\atop 0} \right). \end{equation*} Then \(\varphi\) is a near pseudo-valuation on \(A\). But \(\varphi\) is not a near valuation on \(A\) because there exists \(4\neq0\) and \(\varphi(4)=0\).
The following two examples show that a pseudo-valuation and a near valuation are not identical in general.Example 25. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 2 & 3 & 0 \\ 2 & 0 & 1 & 0 & 0 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.75} \,\,\, {2\atop 0.50} \,\,\, {3\atop 0} \,\,\, {4\atop 0.50} \right). \end{equation*} Then \(\varphi\) is a pseudo-valuation on \(A\). But \(\varphi\) is not a near valuation on \(A\) because there exists \(3\neq0\) and \(\varphi(3)=0\).
Example 26. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 1 & 3 & 3 \\ 2 & 0 & 0 & 0 & 3 & 3 \\ 3 & 0 & 0 & 1 & 0 & 1 \\ 4 & 0 & 0 & 1 & 0 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \ {1\atop 0.25} \ {2\atop 0.30} \ {3\atop 0.40} \ {4\atop 0.90} \right). \end{equation*} Then \(\varphi\) is a near valuation on \(A\). But \(\varphi\) is not a pseudo-valuation on \(A\) because \(\varphi(4)=0.9\nleq0.7=0.4+0.3=\varphi(3)+\varphi(2)=\varphi(2\cdot4)+\varphi(2)\).
The following two examples show that a near pseudo-valuation and a weak valuation are not identical in general.Example 27. Let \(A=\{0,1,2,3,4\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccc} \cdot & 0 & 1 & 2 & 3 & 4 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 2 & 0 & 1 & 0 & 3 & 4 \\ 3 & 0 & 1 & 2 & 0 & 4 \\ 4 & 0 & 1 & 2 & 3 & 0 \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0} \,\,\, {2\atop 0.70} \,\,\, {3\atop 0.30} \,\,\, {4\atop 0.35} \right). \end{equation*} Then \(\varphi\) is a near pseudo-valuation on \(A\). But \(\varphi\) is not a weak valuation on \(A\) because there exists \(1\neq0\) and \(\varphi(1)=0\).
Example 28. Let \(A=\{0,1,2,3,4,5,6\}\) be a UP-algebra with a fixed element \(0\) and a binary operation \(\cdot\) defined by the following Cayley table: \begin{equation*} \begin{array}{c|ccccccc} \cdot & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ \hline 0 & 0 & 1 & 2 & 3 & 4 & 5 & 6 \\ 1 & 0 & 0 & 2 & 3 & 2 & 3 & 6 \\ 2 & 0 & 1 & 0 & 3 & 1 & 5 & 3 \\ 3 & 0 & 1 & 2 & 0 & 4 & 1 & 2 \\ 4 & 0 & 0 & 0 & 3 & 0 & 3 & 3 \\ 5 & 0 & 0 & 2 & 0 & 2 & 0 & 2 \\ 6 & 0 & 1 & 0 & 0 & 1 & 1 & 0 \\ \end{array} \end{equation*} Let \(\varphi\) be a real-valued function on \(A\) defined by \begin{equation*} \varphi = \left( {0\atop 0} \,\,\, {1\atop 0.1} \,\,\, {2\atop 0.2} \,\,\, {3\atop 0.3} \,\,\, {4\atop 0.5} \,\,\, {5\atop 0.2} \,\,\, {6\atop 0.1} \right). \end{equation*} Then \(\varphi\) is a weak valuation on \(A\). But \(\varphi\) is not a near pseudo-valuation as \(\varphi(3\cdot6)=\varphi(2)=0.2\nleq0.1=\varphi(6)\).
Theorem 12. Every weak pseudo-valuation \(\varphi\) on \(A\) satisfies the condition (20).
Proof. For all \(x\in A\), \( \varphi(0) =\varphi(x\cdot x) \leq \varphi(x)+\varphi(x).\) In particular, \(\varphi(0)\leq \varphi(0)+\varphi(0)\), so \(0\leq \varphi(0)\). Hence, \(0\leq\varphi(0)\leq \varphi(x)+\varphi(x)=2\varphi(x)\) for all \(x\in A\), that is, \(0\leq\varphi(x)\) for all \(x\in A\).
Corollary 13. Every \(0\)-weak pseudo-valuation (resp., near pseudo-valuation, pseudo-valuation, valuation, weak valuation, near valuation) \(\varphi\) on \(A\) satisfies the condition (20).
Lemma 1. If \(\varphi\) is a real-valued function on \(A\) satisfying the condition (18) and the following condition:
Proof. For all \(x\in A\), \( \varphi(0) =\varphi(x\cdot x)\leq\varphi(x).\) By (21), we have \(\varphi(0)=0\), that is, \(\varphi\) satisfies the condition (15). Thus \(\varphi\) is a near pseudo-valuation on \(A\). By Corollary 13, we have \(\varphi\) satisfies the condition (20).
Theorem 14. If \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (18) and (21) and the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (18), (21), and (22). By Lemma 1, we have \(\varphi(x)\geq0\) for all \(x\in A\) and \(\varphi(0)=0\). Let \(x,y \in A\). Then \begin{align*} \varphi(y) &=\varphi(0\cdot y)\\ &\leq\varphi(0\cdot x)+\varphi(x\cdot y) \\ &=\varphi(x)+\varphi(x\cdot y)\\ &=\varphi(x\cdot y)+\varphi(x). \end{align*} Hence, \(\varphi\) is a pseudo-valuation on \(A\).
Definition 6. Let \(\varphi\) be a real-valued function on \(A\). Define the subset \(\mathrm{Ker}\,\varphi\) of \(A\) by \begin{equation*} \mathrm{Ker}\,\varphi:=\{x\in A\mid\varphi(x)=0\}. \end{equation*}
Theorem 15. If \(\varphi\) is a pseudo-valuation on \(A\), then \(\mathrm{Ker}\,\varphi\) is a UP-filter of \(A\).
Proof. Assume that \(\varphi\) is a pseudo-valuation on \(A\). By (15), we have \(0\in \mathrm{Ker}\,\varphi\). Let \(x,y\in A\) be such that \(x\cdot y\in \mathrm{Ker}\,\varphi\) and \(x\in \mathrm{Ker}\,\varphi\). Then \(\varphi(x\cdot y)=0\) and \(\varphi(x)=0\). By (16), we have \begin{align*} \varphi(y)\leq\varphi(x\cdot y)+\varphi(x)=0+0=0. \end{align*} It follows from Corollary 13 that \(\varphi(y)=0\), so \(y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a UP-filter of \(A\).
Theorem 16. If \(\varphi\) is a near pseudo-valuation on \(A\), then \(\mathrm{Ker}\,\varphi\) is a near UP-filter of \(A\).
Proof. Assume that \(\varphi\) is a near pseudo-valuation on \(A\). By (15), we have \(0\in \mathrm{Ker}\,\varphi\). Let \(x\in A\) and \(y\in \mathrm{Ker}\,\varphi\). Then \(\varphi(y)=0\). By (18), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(y)=0. \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\), so \(x\cdot y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a near UP-filter of \(A\).
Theorem 17. If \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\), then \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Proof. Assume that \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\). By (15), we have \(0\in \mathrm{Ker}\,\varphi\). Let \(x, y\in A\) be such that \(x\in \mathrm{Ker}\,\varphi\) and \(y\in \mathrm{Ker}\,\varphi\). Then \(\varphi(x)=0\) and \(\varphi(y)=0\). By (19), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(x)+\varphi(y)=0+0=0, \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\), so \(x\cdot y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Theorem 18. If \(\varphi\) is a weak pseudo-valuation on \(A\), then a nonempty subset \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Proof. Assume that \(\varphi\) is a weak pseudo-valuation on \(A\). Let \(\mathrm{Ker}\,\varphi\neq\emptyset\). Let \(x, y\in \mathrm{Ker}\,\varphi\). Then \(\varphi(x)=0\) and \(\varphi(y)=0\). By (19), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(x)+\varphi(y)=0+0=0. \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\), so \(x\cdot y\in \mathrm{Ker}\,\varphi\). Hence, \(\mathrm{Ker}\,\varphi\) is a UP-subalgebra of \(A\).
Proposition 1. Let \(\varphi\) be a pseudo-valuation on \(A\). Then
- (1) \((\forall a,b,x\in A)(a\leq b\cdot x\Rightarrow\varphi(x)\leq\varphi(a)+\varphi(b))\),
- (2) \((\forall x,y\in A)(x\leq y\Rightarrow\varphi(y)\leq \varphi(x))\),
- (3) \((\forall x,y,z\in A)(\varphi(x\cdot z)\leq \varphi(x\cdot y)+\varphi(y\cdot z))\), and
- (4) \((\forall x,y,z\in A)(z\leq x\cdot y\Rightarrow\varphi(z)\leq\varphi(x)+\varphi(y))\).
Proof. (1) Let \(a, b, x \in A\) be such that \(a\leq b\cdot x\). Then \(a\cdot(b\cdot x)=0\). Thus \begin{align*} \varphi(x) &\leq\varphi(b\cdot x)+\varphi(b)\\ &\leq\varphi(a\cdot(b\cdot x))+\varphi(a)+\varphi(b)\\ &=\varphi(0)+\varphi(a)+\varphi(b)\\ &=0+\varphi(a)+\varphi(b)\\ &=\varphi(a)+\varphi(b). \end{align*}
- (2) Let \(x,y\in A\) be such that \(x\leq y\). Then \(x\cdot y=0\). Thus \begin{align*} \varphi(y) &\leq\varphi(x\cdot y)+\varphi(x)\\ &=\varphi(0)+\varphi(x)\\ &=0+\varphi(x)\\ &=\varphi(x). \end{align*}
- (3) Let \(x,y,z\in A\). By (UP-1), we have \(y\cdot z\leq(x\cdot y)\cdot(x\cdot z)\). Thus \begin{align*} \varphi(x\cdot z) &\leq\varphi(y\cdot z)+\varphi(x\cdot y)\\ &=\varphi(x\cdot y)+\varphi(y\cdot z). \end{align*}
- (4) Let \(x,y,z\in A\) be such that \)z\leq x\cdot y\). Then \(z\cdot(x\cdot y)=0\). Thus \begin{align*} \varphi(z) &\leq\varphi(y\cdot z)+\varphi(y)\\ &\leq\varphi(x\cdot(y\cdot z))+\varphi(x)+\varphi(y)\\ &=\varphi(0)+\varphi(x)+\varphi(y)\\ &=0+\varphi(x)+\varphi(y)\\ &=\varphi(x)+\varphi(y). \end{align*}
Theorem 19. If \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\) satisfying the following condition:
Proof. Assume that \(\varphi\) is a \(0\)-weak pseudo-valuation on \(A\) satisfying the condition (23). Clearly, \(\varphi(0)=0\). Let \(x,y\in A\). If \(x\cdot y=0\), it follows from Corollary 13 that \begin{align*} \varphi(x\cdot y)=\varphi(0)=0\leq\varphi(y). \end{align*} If \(x\cdot y\neq0\), it follows from (23) that \(\varphi(x)=0\). By (19), we have \begin{align*} \varphi(x\cdot y)\leq\varphi(x)+\varphi(y)=0+\varphi(y)=\varphi(y). \end{align*} Hence, \(\varphi\) is a near pseudo-valuation on \(A\).
Theorem 20. If \(\varphi\) is a real-valued function on \(A\) satisfying the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the condition (24). Let \(x,y\in A\). By (1), we have \(x\cdot y\leq x\cdot y\). By (24), we have \(\varphi(x\cdot y)\leq\varphi(x)+\varphi(y)\). Hence, \(\varphi\) is a weak pseudo-valuation on \(A\).
Theorem 21. If \(\varphi\) is a real-valued function on \(A\) satisfying the condition (15) and the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (15) and (25). Let \(x\in A\). By (UP-3), we have \(x\leq 0\cdot 0\). By (25) and (15), we have \(\varphi(x)\leq\varphi(0)=0\). By (UP-3) and (1), we have \(0\leq0= x\cdot x\). By (15) and (25), we have \(0=\varphi(0)\leq \varphi(x)\). Thus \(\varphi(x)=0\) for all \(x\in A\), that is, \(\varphi\) is a zero constant real-valued function on \(A\). By Theorem 2, we have \(\varphi\) is a \(0\)-weak pseudo-valuation, a near pseudo-valuation, and a pseudo-valuation on \(A\).
Theorem 22. If \(\varphi\) is a real-valued function on \(A\) satisfying the condition (24) and the following condition:
Proof. Assume that \(\varphi\) is a real-valued function on \(A\) satisfying the conditions (24) and (26). By (UP-3), we have \(0\leq 0\cdot 0\). By (24), we have \(\varphi(0)\leq\varphi(0)+\varphi(0)\) and so \(0\leq\varphi(0)\). By (26), we have \(\varphi(0)=0\), that is, \(\varphi\) satisfies the condition (15). Let \(x\in A\). By (UP-3), we have \(x\leq 0\cdot 0\). By (24) and (15), we have \(\varphi(x)\leq\varphi(0)+\varphi(0)=0+0=0\). By (UP-3), we have \(0\leq x\cdot 0\). By (15) and (24), we have \(0=\varphi(0)\leq\varphi(x)+\varphi(0)=\varphi(x)+0=\varphi(x)\). Thus \(\varphi(x)=0\) for all \(x\in A\), that is, \(\varphi\) is a zero constant real-valued function on \(A\). By Theorem 2, we have \(\varphi\) is a \(0\)-weak pseudo-valuation, a near pseudo-valuation, and a pseudo-valuation on \(A\).
3. Metrics and their generalizations
In this section, we induce a pseudo-metric without triangle inequality, a quasi pseudo-metric, a pseudo-metric, and a metric by some these mappings on a UP-algebra. We also prove that the binary operation defined on a UP-algebra is uniformly continuous under the induced metric by a valuation in some conditions.
Definition 7. Let \(A\) be a nonempty set. A real-valued function \(d\) on \(a\times A\) is called
- (1) a metric on \(A\) if it satisfies the following conditions:
- (M-1) \((\forall x,y\in A)(d(x, y)\geq 0)\),
- (M-2) \((\forall x\in A)(d(x, x) = 0)\),
- (M-3) \((\forall x,y\in A)(d(x, y) = d(y, x))\),
- (M-4) \((\forall x,y,z\in A)(d(x, z)\leq d(x, y) + d(y, z))\), and
- (M-5) \((\forall x,y \in A)(d(x, y) = 0 \Rightarrow x = y)\).
- (2) a pseudo-metric on \(A\) if it satisfies the conditions (M-1), (M-2), (M-3), and (M-4),
- (3) a pseudo-metric without triangle inequality on \(A\) if it satisfies the conditions (M-1), (M-2), and (M-3), and
- (4) a quasi pseudo-metric on \(A\) if it satisfies the conditions (M-1), (M-2), and (M-4).
Theorem 23. Let \(\varphi\) be a \(0\)-weak pseudo-valuation (resp., weak valuation, near pseudo-valuation, near valuation, pseudo-valuation, valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi\) on \(a\times A\) defined by
Proof.
- (M-1) By Corollary 13, we have \(d^{r}_\varphi(x, y)= \dfrac{\varphi(x\cdot y)+\varphi(y \cdot x)}{r}\geq 0\) for all \(x, y\in A\).
- (M-2) Let \(x \in A\). By (1) and (15), we have \(d^{r}_\varphi(x, x) = \dfrac{\varphi(x\cdot x)+\varphi(x\cdot x)}{r} = \dfrac{\varphi(0) + \varphi(0)}{r}=\dfrac{0+0}{r} = 0\).
- (M-3) Let \(x, y \in A\).
Theorem 24. Let \(\varphi\) be a pseudo-valuation (resp., valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) which is defined in (27) is a pseudo-metric on \(A\), called a pseudo-metric induced by a pseudo-valuation (resp., valuation) \(\varphi\).
Proof. By Theorem 23, it suffices to prove (M-4).
- (M-4) Let \(x, y, z\in A\). Then \begin{align*} d^{r}_\varphi(x, y) + d^{r}_\varphi(y, z) &= \dfrac{\varphi(x\cdot y) + \varphi(y\cdot x)}{r} + \dfrac{\varphi(y\cdot z) + \varphi(z\cdot y)}{r}\\ &= \dfrac{\varphi(x\cdot y) + \varphi(y\cdot x) + \varphi(y\cdot z) + \varphi(z\cdot y)}{r}\\ &= \dfrac{\varphi(x\cdot y) + \varphi(y\cdot z)}{r} + \dfrac{\varphi(z\cdot y) + \varphi(y\cdot x)}{r}\\ &\geq\dfrac{\varphi(x\cdot z)}{r}+\dfrac{\varphi(z\cdot x)}{r} \\ &=\dfrac{\varphi(x\cdot z) + \varphi(z\cdot x)}{r}\\ &= d^{r}_\varphi(x, z). \end{align*}
Theorem 25. Let \(\varphi\) be a valuation on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) which is defined in (27) is a metric on \(A\), called a metric induced by a valuation \(\varphi\).
Proof. By Theorem 24, it suffices to prove (M-5).
- (M-5) Let \(x, y\in A\) be such that \(d^{r}_\varphi(x, y)=0\). Then \begin{align*} 0=d^{r}_\varphi(x, y)= \dfrac{\varphi(x\cdot y) + \varphi(y\cdot x)}{r}=\dfrac{\varphi(x\cdot y)}{r}+\dfrac{\varphi(y\cdot x)}{r}. \end{align*} It follows from Corollary 13 that \(\varphi(x\cdot y)=0\) and \(\varphi(y\cdot x)=0\). By (17), we have \(x\cdot y=0\) and \(y\cdot x=0\). By (UP-4), we have \(x=y\). Hence, \(d^{r}_\varphi\) is a metric on \(A\).
Theorem 26. Let \(\varphi\) be a \(0\)-weak pseudo-valuation (resp., weak valuation, near pseudo-valuation, near valuation, pseudo-valuation, valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(d^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) defined by
Proof.
- (M-1) By Corollary 13, we have \(d^{r}_\varphi(x, y)= \dfrac{\varphi(x\cdot y)\times\varphi(y \cdot x)}{r}\geq 0\) for all \(x, y\in A\).
- (M-2) Let \(x \in A\). By (1) and (15), we have \(d^{r}_\varphi(x, x) = \dfrac{\varphi(x\cdot x)\times\varphi(x\cdot x)}{r} = \dfrac{\varphi(0)\times\varphi(0)}{r}=\dfrac{0\times0}{r} = 0\).
- (M-3) Let \(x, y \in A\). Then \(d^{r}_\varphi(x, y) = \dfrac{\varphi(x\cdot y)\times\varphi(y\cdot x)}{r} = \dfrac{\varphi(y\cdot x)\times\varphi(x\cdot y)}{r} = D^{r}_\varphi(y, x)\).
Theorem 27. Let \(\varphi\) be a pseudo-valuation (resp., valuation) on \(A\) and \(r\) be a positive real number. Then the real-valued function \(a^{r}_\varphi : A\times A\rightarrow\mathbb{R}\) defined by
Proof.
- (M-1) By Corollary 13, we have \(a^{r}_\varphi(x, y)= \dfrac{\varphi(x\cdot y)}{r}\geq 0\) for all \(x, y\in A\).
- (M-2) Let \(x \in A\). By (1) and (15), we have \(a^{r}_\varphi(x, x) = \dfrac{\varphi(x\cdot x)}{r} = \dfrac{\varphi(0)}{r}=\dfrac{0}{r} = 0\).
- (M-4) Let \(x, y, z\in A\). Then
Proposition 2. Let \(\varphi\) be a pseudo-valuation on \(A\). Then
Proof. Let \(x, y, a \in A\). By (UP-1) and Proposition 1 (2), we have \(\varphi((a\cdot y)\cdot (a\cdot x))\leq \varphi(y\cdot x)\) and \(\varphi((a\cdot x)\cdot (a\cdot y))\leq \varphi(x\cdot y)\). Thus \begin{align*} d^{r}_\varphi(x, y) &= \dfrac{\varphi(x\cdot y)+\varphi(y\cdot x)}{r}\\ &\geq \dfrac{\varphi((a\cdot x)\cdot (a\cdot y))+\varphi((a\cdot y)\cdot (a\cdot x))}{r}\\ &=d^{r}_\varphi(a\cdot x, a\cdot y). \end{align*}
The following lemma is easily proved.Lemma 2. Let \(a_1, a_2, b_1, b_2\) be real numbers. Then
- (1) \(\max\{a_1, b_1\}+\max\{a_2, b_2\}\geq\max\{a_1+a_2, b_1+b_2\}\), and
- (2) \(\min\{a_1, b_1\}+\min\{a_2, b_2\}\leq\min\{a_1+a_2, b_1+b_2\}\).
Theorem 28. Let \(d\) be a real-valued function on \(a \times A\). Define the real-valued functions \(d^{\circ}\) and \(d_{\circ}\) on \)(A \times A)\times(A \times A)\) by
- (1) if \(d\) satisfies the condition (M-1), then \(d^{\circ}\) and \(d_{\circ}\) satisfy the condition (M-1);
- (2) if \(d\) satisfies the condition (M-2), then \(d^{\circ}\) and \(d_{\circ}\) satisfy the condition (M-2);
- (3) if \(d\) satisfies the condition (M-3), then \(d^{\circ}\) and \(d_{\circ}\) satisfy the condition (M-3);
- (4) if \(d\) satisfies the condition (M-4), then \(d^{\circ}\) satisfies the condition (M-4);
- (5) if \(d\) satisfies the condition (M-5), then \(d^{\circ}\) satisfies the condition (M-5).
Proof.
- (1) Assume that \(d\) satisfies the condition (M-1). Let \)(x, y),(a, b)\in A\times A\). Since \(d(x, a)\geq 0\) and \(d(y, b)\geq0\), we have \[d^{\circ}((x, y),(a, b))=\max\{d(x, a), d(y, b)\}\geq 0\] and \[d_{\circ}((x, y),(a, b))=\min\{d(x, a), d(y, b)\}\geq 0.\] Hence, \(d^{\circ}\) and \(d_{\circ}\) satisfy the condition (M-1).
- (2) Assume that \(d\) satisfies the condition (M-2). Since \(d(x, x)=0\) and \(d(y, y)=0\), we have \[d^{\circ}((x, y),(x, y))=\max\{d(x, x), d(y, y)\}=\max\{0, 0\}= 0\] and \[d_{\circ}((x, y),(x, y))=\min\{d(x, x), d(y, y)\}=\min\{0, 0\}= 0.\] Hence, \(d^{\circ}\) and \(d_{\circ}\) satisfy the condition (M-2).
- (3) Assume that \(d\) satisfies the condition (M-3). Since \(d(x, a)=d(a, x)\) and \(d(y, b)=d(b, y)\), we have \[d^{\circ}((x, y),(a, b))=\max\{d(x, a), d(y, b)\})=\max\{d(a, x), d(b, y)\}=d^{\circ}((a, b),(x, y))\] and \[d_{\circ}((x, y),(a, b))=\min\{d(x, a), d(y, b)\})=\min\{d(a, x), d(b, y)\}=d_{\circ}((a, b),(x, y)).\] Hence, \(d^{\circ}\) and \(d_{\circ}\) satisfy the condition (M-3).
- (4) Assume that \(d\) satisfies the condition (M-4). Since \(d(x, u)+ d(u, a)\geq d(x, a)\) and \(d(y, v)+ d(v, b)\geq d(y, b)\), we have \begin{align*} d^{\circ}((x, y), (u, v)) +d^{\circ}((u, v), (a, b))&= \max\{d(x, u), d(y, v)\} + \max\{d(u, a), d(v, b)\}\\ &\geq \max\{d(x, u)+ d(u, a),d(y, v)+ d(v, b)\}\\ &\geq\max\{d(x, a), d(y, b)\}\\ &=d^{\circ}((x, y), (a, b)). \end{align*} Hence, \(d^{\circ}\) satisfies the condition (M-4).
- (5) Assume that \(d\) satisfies the condition (M-5). Let \((x, y), (a, b)\in A\times A\) be such that \(d^{\circ}((x, y), (a, b))=0\). Then \[0=d^{\circ}((x, y), (a, b))= \max\{d(x, a), d(y, b)\}.\] Thus \(0\geq d(x, a)\) and \(0\geq d(y, b)\). Since \(d(x, a)\geq 0\) and \(d(y, b)\geq 0\), we have \(d(x, a)= 0\) and \(d(y, b)= 0\). By (M-5) of \(d\), we have \(x=a\) and \(y=b\). Thus \((x, y)=(a, b)\). Hence, \(d^{\circ}\) satisfies the condition (M-5).
Theorem 29. Let \(d\) be a real-valued function on \(A\times A\). Then
- (1) if \(d\) is a pseudo-metric without triangle inequality on \(A\), then \(d^{\circ}\) and \(d_{\circ}\) are pseudo-metrics without triangle inequality on \(A\times A\);
- (2) if \(d\) is a quasi pseudo-metric on \(A\), then \(d^{\circ}\) is a quasi pseudo-metric on \(A\times A\);
- (3) if \(d\) is a pseudo-metric on \(A\), then \(d^{\circ}\) is a pseudo-metric on \(A\times A\);
- (4) if \(d\) is a metric on \(A\), then \(d^{\circ}\) is a metric on \(A\times A\).
Proof. It is straightforward from Theorem 28.
Corollary 30. If \(\varphi\) is a \(0\)-weak pseudo-valuation (resp., weak valuation, near pseudo-valuation, near valuation, pseudo-valuation, valuation) on \(A\) and \(r\) is a positive real number, then \((d^{r}_\varphi)^{\circ}, (d^{r}_\varphi)_{\circ}, (D^{r}_\varphi)^{\circ}\), and \((D^{r}_\varphi)_{\circ}\) are pseudo-metrics without triangle inequality on \(A\times A\).
Proof. It is straightforward from Theorems 23,26 and 29(1).
Corollary 31. If \(\varphi\) is a pseudo-valuation (resp., valuation) on \(A\) and \(r\) is a positive real number, then \((d^{r}_\varphi)^{\circ}\) is a pseudo-metric and \((A^{r}_\varphi)^{\circ}\) is a quasi pseudo-metric on \(A\times A\).
Proof. It is straightforward from Theorems 24,27,29(2) and 29(3).
Corollary 32. If \(\varphi\) is a valuation on \(A\) and \(r\) is a positive real number, then \((d^{r}_\varphi)^{\circ}\) is a metric on \(A\times A\).
Proof. It is straightforward from Theorems 25 and 29(4).
We recall the definition of a uniformly continuous function of metric spaces:
Definition 8. Let metric spaces \((X, d_1)\) and \((Y, d_2)\), a function \(f : X \rightarrow Y\) is said to be uniformly continuous if for every real number \(\varepsilon > 0\) there exists a real number \(\delta > 0\) such that \begin{equation*} (\forall x,y\in X)(d_1(x, y) < \delta\Rightarrow d_2(f(x), f(y)) < \varepsilon). \end{equation*}
Theorem 33. If \(\varphi\) is a valuation on \(A\) with \(\inf\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}>0\) exists, then the binary operation \(\cdot\) on \(A\) is uniformly continuous.
Proof. Assume that \(\varphi\) is a valuation on a finite UP-algebra \(A\) with more than one element. By Theorem 25 and Corollary 32, we have \((A, d^{r}_\varphi)\) and \((A\times A, (d^{r}_\varphi)^{\circ})\) are metric spaces. Let \(\varepsilon>0\). Choose \(\delta=\inf\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}\). Let \((x,y), (a, b)\in A\times A\) be such that \((d^{r}_\varphi)^{\circ}((x,y), (a, b))< \delta\). Then \((d^{r}_\varphi)^{\circ}((x,y), (a, b))=0\). By (M-5), we have \((x,y)=(a, b)\) and so \(x=a\) and \(y=b\). Thus, by (M-2), we have \(d^{r}_\varphi(\cdot(x,y), \cdot(a, b))=d^{r}_\varphi(\cdot(x,y), \cdot(x, y))=d^{r}_\varphi(x\cdot y, x\cdot y)=0< \varepsilon\). Hence, the binary operation \(\cdot\) on \(A\) is uniformly continuous.
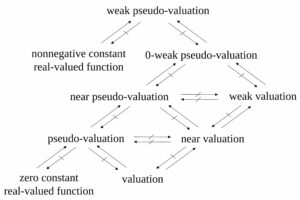
Figure 1. Valuations and their generalizations for UP-algebras
Theorem 34. If \(\varphi\) is a valuation on a finite UP-algebra \(A\) with more than one element, then the binary operation \(\cdot\) on \(A\) is uniformly continuous.
Proof. Assume that \(\varphi\) is a valuation on a finite UP-algebra \(A\) with more than one element. By (M-1) and (M-5) and \(A\times A\) has more than one element, we have \(\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}\) is a finite nonempty subset of \(\mathbb{R}\). Thus \(\inf\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}=\min\{(d^{r}_\varphi)^{\circ}((x,y), (a, b))\mid(d^{r}_\varphi)^{\circ}((x,y), (a, b))>0\}\) exists. By Theorem 33, we have the binary operation \(\cdot\) on \(A\) is uniformly continuous.
Conclusions
In this paper, we have introduced the notions of a weak pseudo-valuation, a \(0\)-weak pseudo-valuation, a weak valuation, a near pseudo-valuation, a near valuation, a pseudo-valuation, and a valuation and induced a pseudo-metric without triangle inequality, a quasi pseudo-metric, a pseudo-metric, and a metric by some these mappings on a UP-algebra. Then, we get the diagram of generalization of these mappings on a UP-algebra as shown in Figure 1 (see Theorems 1,2,4,5,6,7,8,9,10,11).Acknowledgments
This work was supported by the Unit of Excellence, University of Phayao. The authors would also like to thank the anonymous referee for giving many helpful suggestion on the revision of present paper.Authorcontributions
All authors contributed equally in writing of this paper. All authors read and approved the final manuscript.Conflictofinterests
The authors declare no conflict of interest.References
- Buşneag, D. (1996). Hilbert algebras with valuations. Mathematica japonicae, 44(2), 285-289.[Google Scholor]
- Buşneag, D. (2003). On extensions of pseudo-valuations on Hilbert algebras. Discrete Mathematics, 263(1-3), 11-24.[Google Scholor]
- Buşneag, C. (2007). Valuations on residuated lattices. Annals of the University of Craiova-Mathematics and Computer Science Series, 34, 21-28.[Google Scholor]
- Doh, M. I., & Kang, M. S. (2010). BCK/BCI-algebras with pseudo-valuations. Honam Mathematical Journal, 32(2), 217-226. [Google Scholor]
- Ghorbani, S. (2010). Quotient BCI-algebras induced by pseudo-valuations. Iranian Journal of Mathematical Sciences and Informatics, 5(2), 13-24.[Google Scholor]
- Doh, M. I., & Kang, M. S. (2011). Commutative pseudo valuations on BCK-algebras. International Journal of Mathematics and Mathematical Sciences, Volume 2011, Article ID 754047.[Google Scholor]
- Jun, Y. B., Lee, K. J., & Ahn, S. S. (2011). Positive implicative pseudo-valuations on BCK-algebras. Journal of Applied Mathematics, 5, 651-662.[Google Scholor]
- Jun, Y. B., Ahn, S. S., & Roh, E. H. (2012). BCC-algebras with pseudo-valuations. Filomat, 26(2), 243-252. [Google Scholor]
- Zhan, J., & Jun, Y. B. (2013). (Implicative) pseudo-valuations on R-0-algebras. University Politehnica of Bucharest Scientific Bulletin-Series A-Applied Mathematics and Physics, 75(4), 101-112. [Google Scholor]
- Lee, K. J. (2013). Pseudo-valuations on BE-algebras. Applied Mathematical Sciences, 7(125), 6199-6207. [Google Scholor]
- Song, S. Z., Roh, E. H., & Jun, Y. B. (2015). Quasi-valuation maps on BCK/BCI-algebras. Kyungpook Mathematical Journal, 55(4), 859-870.[Google Scholor]
- Yang, Y., & Xin, X. (2017). EQ-algebras with pseudo pre-valuations. Italian Journal of Pure and Applied Mathematics, 36, 29-48.[Google Scholor]
- Mehrshad, S., & Kouhestani, N. (2018). On pseudo-valuations on BCK-algebras. Filomat, 32(12), 4319-4332. [Google Scholor]
- Koam, A. N., Haider, A., & Ansari, M. A. (2019). Pseudo-metric on KU-algebras. The Korean Journal of Mathematics, 27(1), 131-140.[Google Scholor]
- Ali, U., Ansari, M. A., & Rehman, M. U. (2019). Pseudo-valuations and pseudo-metric on JU-algebras. Open Journal of Mathematical Sciences, 3(1), 440-446.[Google Scholor]
- Romano, D. A. (2019). Pseudo-valuations on UP-algebras. Universal Journal of Mathematics and Applications, 2(3), 138-140. [Google Scholor]
- Iampan, A. (2017). A new branch of the logical algebra: UP-algebras. Journal of Algebra and Related Topics, 5(1), 35-54. [Google Scholor]
- Prabpayak, C., & Leerawat, U. (2009). On ideals and congruences in KU-algebras. Scientia Magna, 5(1), 54-57.[Google Scholor]
- Satirad, A., Mosrijai, P., & Iampan, A. (2019). Generalized power UP-algebras. Computer Science, 14(1), 17-25. [Google Scholor]
- Dokkhamdang, N., Kesorn, A., & Iampan, A. (2018). Generalized fuzzy sets in UP-algebras. Annals of Fuzzy Mathematics and Informatics, 16(2), 171-190.[Google Scholor]
- Songsaeng, M., & Iampan, A. (2018). \( mathcal {N} \)-Fuzzy UP-Algebras and its level subsets. Journal of Algebra and Related Topics, 6(1), 1-24.[Google Scholor]
- Ansari, M. A., Haidar, A., & Koam, A. N. (2018). On a graph associated to UP-algebras. Mathematical and Computational Applications, 23(4), 61.[Google Scholor]
- Ansari, M. A., Koam, A. N., & Haider, A. (2019). Rough set theory applied to UP-algebras. Italian Journal of Pure and Applied Mathematics, 42, 388-402.[Google Scholor]
- Iampan, A. (2018). Introducing fully UP-semigroups. Discussiones Mathematicae-General Algebra and Applications, 38(2), 297-306.[Google Scholor]
- Satirad, A., Mosrijai, P., & Iampan, A. (2019). Formulas for finding UP-algebras. International Journal of Mathematics and Computer Science, 14(2), 403-409.[Google Scholor]
- Iampan, A. (2017). Fuzzy translations of a fuzzy set in UP-algebras. Journal of the Indonesian Mathematical Society, 23(2), 1-19.[Google Scholor]
- Iampan, A. (2019). Multipliers and near UP-filters of UP-algebras. Journal of Discrete Mathematical Sciences and Cryptography, 1-14.[Google Scholor]
- Somjanta, J., Thuekaew, N., Kumpeangkeaw, P., & Iampan, A. (2016). Fuzzy sets in UP-algebras. Annals of Fuzzy Mathematics and Informatics, 12(6), 739-756.[Google Scholor]