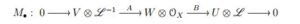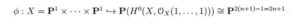Vector bundles associated to monads on cartesian products of projective spaces

1. Introduction

In algebraic geometry, one very interesting problem deals with the existence of indecomposable vector bundles of low rank on algebraic varieties in comparison to the ambient space. One of the most important tools or technique to construct these vector bundles is via monads which appear in many contexts within algebraic geometry. Monads were first introduced by Horrocks [1] who showed that all vector bundles \(E\) on \(\mathbf{P}^3\) could be obtained as the cohomology bundle of a monad of a given kind.

Many authors have constructed indecomposable vector bundles of low over projective varieties, we mention a few of the pioneers that have made remarkable strides in this regard. The famous Horrocks-Mumford bundle of rank 2 over \(\mathbf{P}^4\) [2], the Horrocks vector bundle of rank 3 on \(\mathbf{P}^5\) [3] the Tango bundles [4] of rank \(n-1\) on \(\mathbf{P}^n\) for \(n\geq3\) and the rank 2 vector bundle on \(P^5\) in characteristic 2 by Tango [4] are all obtained as cohomologies of certain monads.

The first problem is to tackle the existence of monads. Fløystad [5] gave a theorem on the existence of monads over projective spaces. Costa and Miró-Roig [6] extended these results to smooth quadric hypersurfaces of dimension at least 3. Marchesi, Marques and Soares [7] generalized Fløystad's theorem to a larger set of varieties. Maingi [8] proved the existence of monads on \(\mathbf{P}^n\times\mathbf{P}^n\) and proved simplicity of the cohomology bundle.

In this work we prove the existence of monads on certain Cartesian products of projective spaces. We first extend Fløystad's [6] main theorem to \(\mathbf{P}^1\times\cdots\times\mathbf{P}^1\). Maingi [9] gave a conditional variant theorem on \(\mathbf{P}^{a_1}\times\cdots\times\mathbf{P}^{a_n}\), here we give a biconditional theorem (Theorem 4) but for all \(a_i=1\), \(i=1,\cdots,n+1\). Next we establish the existence of monads \[0\rightarrow{\mathcal{O}_X(-1,-1,-1,-1)^{\oplus k}} 0\overrightarrow{f}>{\mathscr{G}_n\oplus \mathscr{G}_m}\overrightarrow{g}>\mathcal{O}_X(1,1,1,1)^{\oplus k} 0\rightarrow0\] on \(X=\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\) where \(\mathscr{G}_n:=\mathcal{O}_X(0,-1,0,0)^{\oplus n+k}\oplus\mathcal{O}_X(-1,0,0,0)^{\oplus n+k}\) and \(\mathscr{G}_m:=\mathcal{O}_X(0,0,-1,0)^{\oplus m+k}\oplus\mathcal{O}_X(0,0,0,-1)^{\oplus m+k}\). We then prove stability of the kernel bundle \(\ker g\) and finally prove that the cohomology vector bundle, \(E=\ker g/ im f\) is simple. The first set of definitions in the following section are based on lecture notes by Miró-Roig [10].

3. Preliminaries

Definition 1. Let \(X\) be a nonsingular projective variety.

1. A monad on \(X\) is a complex of vector bundles:

with \(\alpha\) injective and \(\beta\) surjective equivalently, \(M_\bullet\) is a monad if \(\alpha\) and \(\beta\) are of maximal rank and \(\beta\circ\alpha = 0\).

The vector bundle \(E = \ker(\beta) im (\alpha)\) and is called the cohomology bundle of the monad.

The kernel of the map \(\beta\), \(\ker\beta\) and the cokernel of \(\alpha\), \(coker \alpha\) for the given monad are vector bundles.

The rank of \(E\) is given by, \(rank(E)= rank(M_0)-rank(M_1)-rank(M_2)\).

The \(i^{th}\) chern class of \(E\) is given by, \(c_i(E)= c_i(M_0)c_i(M_1)^{-1}c_i(M_2)^{-1}\).

Definition 2. Let \(X\) be a nonsingular projective variety, let \(\mathscr{L}\) be a very ample line sheaf, and \(V,W,U\) be finite dimensional \(k\)-vector spaces. A linear monad on \(X\) is a complex of sheaves,

where \(A\in Hom(V,W)\otimes H^0 \mathscr{L}\) is injective and \(B\in Hom(W,U)\otimes H^0 \mathscr{L}\) is surjective. The existence of the monad \(M_\bullet\) is equivalent to the following conditions on \(A\) and \(B\)

1. \(A\) and \(B\) are of maximal rank.
2. \(BA\) is the zero matrix.

Definition 3. A torsion-free sheaf \(E\) on \(X\) is said to be a linear sheaf on \(X\) if it can be represented as the cohomology sheaf of a linear monad.

Definition 4. Let \(X\) be a non-singular irreducible projective variety of dimension \(d\) and let \(\mathscr{L}\) be an ample line bundle on \(X\). For a torsion-free sheaf \(F\) on \(X\) we define

1. the degree of \(F\) relative to \(\mathscr{L}\) as \(\deg_{\mathscr{L}}F:= c_1(F)\cdot \mathscr{L}^{d-1}\),
2. the slope of \(F\) as \(\mu_{\mathscr{L}}(F):= \frac{c_1(F)\mathscr{L}^{d-1}}{rk(F)}\).

Definition 5. Let \(X\) be an algebraic variety and let \(E\) be a torsion-free sheaf on \(X\). Then \(E\) is \(\mathscr{L}\)-stable if every subsheaf \(F\hookrightarrow E\) satisfies \(\mu_{\mathscr{L}}(F)< \mu_{\mathscr{L}}(E)\), where \(\mathscr{L}\) is an ample invertible sheaf.

2.1. Hoppe's Criterion over cyclic varieties

Suppose that the picard group Pic\((X) \simeq Z\) such varieties are called cyclic. Given a holomorphic vector bundle) \(E\rightarrow X\), there is a unique integer \(k_E\) such that \(-r + 1 \leq c_1(E(-k_E)) \leq 0\). Setting \(E_{norm} := E(-k_E)\), we say \(E\) is normalized if \(E = E_{norm}\). Then one has the following stability criterion:

Proposition 1. ([11], Lemma 2.6) Let \(E\) be a rank \(r\) holomorphic vector bundle over a cyclic projective variety \(X\). If \(H^0((\bigwedge^q E)_{norm}) = 0\) for \(1\leq q\leq r-1\), then \(E\) is stable and \(E\) is semistable if \(H^0((\bigwedge^q E)_{norm}(-1)) = 0\).

2.2. Hoppe's Criterion over polycyclic varieties

Suppose that the picard group Pic\((X) \simeq Z^l\) where \(l\geq2\) is an integer then \(X\) is a polycyclic variety. Given a divisor \(B\) on \(X\) we define \(\delta_{\mathscr{L}}(B):= \deg_{\mathscr{L}}\mathcal{O}_{X}(B)\). Then one has the following stability criterion ([12], Theorem 3):

Theorem 1.[Generalized Hoppe Criterion] Let \(G\rightarrow X\) be a holomorphic vector bundle of rank \(r\geq2\) over a polycyclic variety \(X\) equiped with a polarisation \(\mathscr{L}\) if \[H^0(X,(\wedge^sG)\otimes\mathcal{O}_X(B))=0\,,\] for all \(B\in pic(X)\) and \(s\in\{1,\ldots,r-1\}\) such that \(\delta_{\mathscr{L}}(B)< -s\mu_{\mathscr{L}}(G)\) then \(G\) is stable and if \(\delta_{\mathscr{L}}(B)\leq-s\mu_{\mathscr{L}}(G)\) then \(G\) is semi-stable. Conversely if then \(G\) is (semi-)stable then \[H^0(X,G\otimes\mathcal{O}_X(B))=0\] for all \(B\in pic(X)\) and all \(s\in\{1,\ldots,r-1\}\) such that \(\delta_{\mathscr{L}}(B)< -s\mu_{\mathscr{L}}(G)\) or \(\delta_{\mathscr{L}}(B)\leq-s\mu_{\mathscr{L}}(G)\).

2.3. Hoppe's Criterion over \(X=\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\)

Suppose the ambient space is \(X=\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\) then \( pic(X) \simeq Z^4\). We denote by \(a, b,c,d\) the generators of \( pic(X)\). Denote by \(\mathcal{O}_X(a,b,c,d):= {p_1}^*\mathcal{O}_{\mathbf{P}^n}(a)\otimes {p_2}^*\mathcal{O}_{\mathbf{P}^n}(b)\otimes {p_3}^*\mathcal{O}_{\mathbf{P}^m}(c)\otimes {p_4}^*\mathcal{O}_{\mathbf{P}^m}(d)\), where \(p_1\) and \(p_2\) are natural projections from \(X\) to \(\mathbf{P}^n\) and \(p_3\) and \(p_4\) are natural projections from \(X\) to \(\mathbf{P}^m\). For any line bundle \(\mathscr{L} = \mathcal{O}_X(a,b,c,d)\) on \(X\) and a vector bundle \(E\), we will write \(E(a,b,c,d) = E\otimes\mathcal{O}_X(a,b,c,d)\) and \((a,b,c,d):= 1\cdot[a\times\mathbf{P}^n]+1\cdot[\mathbf{P}^n\times b]+1\cdot[c\times\mathbf{P}^m]+1\cdot[\mathbf{P}^m\times d]\) to represent its corresponding divisor. The normalization of \(E\) on \(X\) with respect to \(\mathscr{L}\) is defined as follows: Set \(d=\deg_{\mathscr{L}}(\mathcal{O}_X(1,0,0,0))\), since \(\deg_{\mathscr{L}}(E(-k_E,0,0,0))=\deg_{\mathscr{L}}(E)-4k\cdot rank(E)\) there's a unique integer \(k_E:=\lceil\mu_\mathscr{L}(E)/d\rceil\) such that \(1 - d.rank(E)\leq \deg_\mathscr{L}(E(-k_E,0,0,0))\leq0\). The twisted bundle \(E_{{\mathscr{L}}-norm}:= E(-k_E,0,0,0)\) is called the \(\mathscr{L}\)-normalization of \(E\). Finally we define the linear functional \(\delta_{\mathscr{L}}\) on \(\mathbb{Z}^4\) as \(\delta_{\mathscr{L}}(p_1,p_2,p_3,p_4):= \deg_{\mathscr{L}}\mathcal{O}_{X}(p_1,p_2,p_3,p_4)\).

Proposition 2. Let \(X\) be a polycyclic variety with Picard number \(4\), let \(\mathscr{L}\) be an ample line bundle and let E be a rank \(r>1 \) holomorphic vector bundle over \(X\). If \(H^0((\bigwedge^q E)_{{\mathscr{L}}-norm}(p_1,p_2,p_3,p_4)) = 0\) for \(1\leq q \leq r-1\) and every \((p_1,p_2,p_3,p_4)\in \mathbb{Z}^4\) such that \(\delta_{\mathscr{L}}\leq0\) then E is \(\mathscr{L}\)-stable.

Definition 6. A vector bundle \(E\) on \(X\) is said to be

1. indecomposable if it does not admit a direct sum decomposition of two proper vector subbundles \(E_1\) and \(E_2\) otherwise \(E\) is decomposable.
2. simple if its only endomorphisms are the homotheties i.e. \(Hom(E,E)=k\) equivalently \(h^0(X,E\otimes E^*)=1\).

Proposition 3. Let \(0\rightarrow E \rightarrow F \rightarrow G\rightarrow 0\) be an exact sequence of vector bundles. Then we have the following exact sequences involving exterior and symmetric powers:

1. \(0\rightarrow \bigwedge^q E \rightarrow \bigwedge^q F \rightarrow \bigwedge^{q-1} F\otimes G\rightarrow \cdots \rightarrow F\otimes S^{q-1}G \rightarrow S^{q}G\rightarrow 0\),
2. \(0\rightarrow S^{q}E \rightarrow S^{q-1}E\otimes F \rightarrow \cdots \rightarrow E\otimes\bigwedge^{q-1}F\rightarrow \bigwedge^q F \rightarrow \bigwedge^q G\rightarrow 0\).

Theorem 2.[Künneth formula] Let \(X\) and \(Y\) be projective varieties over a field \(k\). Let \(\mathscr{F}\) and \(\mathscr{G}\) be coherent sheaves on \(X\) and \(Y\) respectively. Let \(\mathscr{F}\boxtimes\mathscr{G}\) denote \(p_1^*(\mathscr{F})\otimes p_2^*(\mathscr{G})\), then \(\displaystyle{H^m(X\times Y,\mathscr{F}\boxtimes\mathscr{G}) \cong \bigoplus_{p+q=m} H^p(X,\mathscr{F})\otimes H^q(Y,\mathscr{G})}\).

Since for our case we deal \(X = \mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\), then \[\displaystyle{H^t(X,\mathcal{O}_X (i,j,k,l)) \cong \bigoplus_{p+q+r+s=t} U\otimes V}\,,\] where \(U = H^p(\mathbf{P}^n,\mathcal{O}_{\mathbf{P}^n}(i))\otimes H^q(\mathbf{P}^n,\mathcal{O}_{\mathbf{P}^n}(j))\), \(V=H^r(\mathbf{P}^m,\mathcal{O}_{\mathbf{P}^m}(k)))\otimes H^s(\mathbf{P}^m,\mathcal{O}_{\mathbf{P}^m}(l))\) and \(p,q,r,s,t,i,j,k\) and \(l\) are integers.

Theorem 3. ([13], Theorem 4.1) Let \(n\geq1\) be an integer and \(d\) be an integer. We denote by \(S_d\) the space of homogeneous polynomials of degree \(d\) in \(n+1\) variables (conventionally if \(d< 0\) then \(S_d=0\)). Then the following statements are true:

1. \(H^0(\mathbf{P}^n,\mathcal{O}_{\mathbf{P}^n}(d))=S_d\) for all \(d\).
2. \(H^i(\mathbf{P}^n,\mathcal{O}_{\mathbf{P}^n}(d))=0\) for \(1< i< n\) and for all \(d\).
3. \(H^n(\mathbf{P}^n,\mathcal{O}_{\mathbf{P}^n}(d))\cong H^0(\mathbf{P}^n,\mathcal{O}_{\mathbf{P}^n}(-d-n-1))\).

We adopt a lemma by Jardim and Earp ( [14], Lemma 9) for our purpose in this work.

Lemma 1. If \(p_1+p_2+p_3+p_4>0\) then \(h^p(X,\mathcal{O}_X (-p_1,-p_2,-p_3,-p_4)^{\oplus k}) = 0\) where \(X = \mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\) and for \(0\leq p< \dim(X) -1\), for \(k\) a non negative integer.

Lemma 2.( [14], Lemma 10) Let \(A\) and \(B\) be vector bundles canonically pulled back from \(A'\) on \(\mathbf{P}^n\) and \(B'\) on \(\mathbf{P}^m\) then \(\displaystyle{H^q(\bigwedge^s(A\otimes B))= \sum_{k_1+\cdots+k_s=q}\big\{\bigoplus_{i=1}^{s}(\sum_{j=0}^s\sum_{m=0}^{k_i}H^m(\wedge^j(A))\otimes(H^{k_i-m}(\wedge^{s-j}(B)))) \big\}}\).

The proof of the lemma depends on the following:

1. \(\displaystyle{H^q(A_1\oplus\cdots\oplus A_s) = \sum_{k_1+\cdots+k_s=q}\big\{\bigoplus_{i=1}^{s}H^k_i(A_i)\big\}}\).
2. \(\displaystyle{H^q(A\otimes B)=\sum_{m=0}^qH^m(A)\otimes H^{q-m}(B)}\).
3. \(\displaystyle{\wedge^s(A\otimes B)=\sum_{j=0}^s\wedge^j(A)\otimes\wedge^{s-j}(B)}\).

4. Main Results

The goal of this section is to construct monads over the Cartesian products of projective spaces. We first give sufficient and necessary conditions for the existence of monads on \(\mathbf{P}^1\times\cdots\times\mathbf{P}^1\). Next we establish the existence of monads on \(\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\), we then proceed to prove stability and simplicity of the cohomology bundle \(E\) associated to these monads on \(\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\). We start by recalling the existence and classification of linear monads on \(\mathbf{P}^n\) given by Fløystad in [5].

Lemma 3.([5], Main Theorem) Let \(k\geq1\). There exists monads on \(\mathbf{P}^k\) whose maps are matrices of linear forms, \[ 0\rightarrow {\mathcal{O}_{\mathbf{P}^{k}}(-1)^{\oplus a}} \underrightarrow{A}>{\mathcal{O}^{\oplus b}_{\mathbf{P}^{k}}} \underrightarrow{B}>{\mathcal{O}_{\mathbf{P}^{k}}(1)^{\oplus c}} \rightarrow 0\\ \] if and only if at least one of the following is fulfilled;
\((1)b\geq2c+k-1\) , \(b\geq a+c\) and
\((2)b\geq a+c+k\)

Theorem 4. Let \(X = \mathbf{P}^1\times\mathbf{P}^1\cdots\times\mathbf{P}^1\) and \(\mathscr{L} = \mathcal{O}_X(1,\cdots,1)\) an ample line bundle. Denote by \(N = h^0(\mathcal{O}_X(1,\cdots,1)) - 1=2n+1\). Then there exists a linear monad \(M_\bullet\) on \(X\) of the form \[ M_\bullet: 0\rightarrow \mathcal{O}_{X}(-1,\cdots,-1)^{\oplus\alpha}\underrightarrow{f}{\mathcal{O}^{\oplus\beta}_X} \underrightarrow{g}\mathcal{O}_{X}(1,\cdots,1)^{\oplus\gamma} \rightarrow 0\\ \] if and only if atleast one of the following is satified

1. \(\beta\geq 2\gamma + N -1\), and \(\beta\geq \alpha + \gamma\),
2. \(\beta\geq \alpha + \gamma + N\), where \(\alpha,\beta, \gamma\) be positive integers.

Proof For the ample line bundle \(\mathscr{L} = \mathcal{O}_X(1,\ldots,1)\) we have the Segre embedding

Suppose that one of the conditions of Lemma 3 is satisfied and setting \(k=2n+1\), \(\alpha=a\), \(\beta=b\) and \(\gamma=c\), we see that

1. \(b=\beta\geq2c+k-1=2\gamma+N-1\) i.e. \(\beta\geq2\gamma+N-1\) and \(\beta\geq \alpha + \gamma\) follows.
2. \(\beta\geq \alpha + \gamma + N\), for \(N=k\).

Thus there exists a linear monad \[ 0\rightarrow {\mathcal{O}_{\mathbf{P}^{2n+1}}(-1)^{\oplus\alpha}} \underrightarrow{A}>{\mathcal{O}^{\oplus\beta}_{\mathbf{P}^{2n+1}}} \underrightarrow{B}>{\mathcal{O}_{\mathbf{P}^{2n+1}}(1)^{\oplus\gamma}} \rightarrow 0 \] on \(\mathbf{P}^{2n+1}\). Notice that the maps \(A\) and \(B\) are defined as follows; \begin{align*} A\in Hom(\mathcal{O}_{\mathbf{P}^{2n+1}}(-1)^{\oplus\alpha},\mathcal{O}_{\mathbf{P}^{2n+1}}^{\oplus\beta})\cong H^0(\mathbf{P}^{2n+1},\mathcal{O}_{\mathbf{P}^{2n+1}}(1)^{\oplus\alpha\beta}) \,, \\ B\in Hom(\mathcal{O}_{\mathbf{P}^{2n+1}}^{\oplus\beta},\mathcal{O}_{\mathbf{P}^{2n+1}}(1)^{\oplus\gamma})\cong H^0(\mathbf{P}^{2n+1},\mathcal{O}_{\mathbf{P}^{2n+1}}(1)^{\oplus\beta\gamma})\,. \end{align*} Thus, \(A\) and \(B\) induce a monad on \(X\), a Cartesian product of \(n+1\) copies of \(\mathbf{P}^1\): \[ 0\rightarrow {\mathcal{O}_{X}(-1,\ldots,-1)^{\oplus\alpha}} \underrightarrow{\bar{A}}{\mathcal{O}^{\oplus\beta}_X}\underrightarrow{\bar{B}}{\mathcal{O}_{X}(1,\ldots,1)^{\oplus\gamma}} \rightarrow 0\,, \] where \(\bar{A}\in Hom(\mathcal{O}_{X}(-1,\ldots,-1)^{\oplus\alpha},\mathcal{O}^{\oplus\beta}_X)\) and \(\bar{B}\in Hom(\mathcal{O}^{\oplus\beta}_X , \mathcal{O}_{X}(1,\ldots,1)^{\oplus\gamma})\). Conversely suppose \[ M_\bullet:0\rightarrow {\mathcal{O}_{X}(-1,\ldots,-1)^{\oplus\alpha}} \underrightarrow{f}{\mathcal{O}^{\oplus\beta}_X} \underrightarrow{g}{\mathcal{O}_{X}(1,\ldots,1)^{\oplus\gamma}} \rightarrow 0 \] exists. We need to prove the necessity of conditions on \(\alpha,\beta\) and \(\gamma\). Then we first notice that the existence of the monad \(M_\bullet\) implies that \(\beta\geq \alpha+\gamma\). The image of \(H^0({\mathcal{O}^{\oplus\beta}_X}) \rightarrow H^0(\mathcal{O}_{X}(1,\cdots,1)^{\oplus\gamma})\) defines a vector subspace \(V \subseteq H^0(\mathcal{O}_{X}(1,\cdots,1)^{\oplus\gamma})\) since \(g\) is surjective. We then have the diagram:

Also \(\dim V\geq \gamma+N\) otherwise \(g\) would degenerate in a non-empty subscheme of codimension \(\dim V -\gamma+1\), see [15 14.4.13]. Let \(U\) a subspace of \(V\) be a general subspace of dimension \(\gamma+N-1\). Then the map \(U\otimes \mathcal{O}_X \rightarrow \mathcal{O}_X(1,\cdots,1)^{\oplus\gamma})\) degenerates in dimension zero by [15]. Fix a splitting \( V \rightarrow H^0({\mathcal{O}^{\beta}_X}) \rightarrow V\). Let \(W=H^0(\mathcal{O}^{\beta}_X)/U\) and \(R = k[x_0,\cdots,x_N]\). We get a diagram of free \(R-\)modules

Let \(\overline{p}\) and \(\overline{q}\) denote the corresponding maps of sheaves. We note that there exists a surjection map \[ coker \overline{q} \rightarrow coker \overline{p} \rightarrow 0\,,\] since \(\overline{p}\) degenerates in expected codimension [16] Theorem 2.3], we have \[ Fitt_1(coker \overline{p}) = Ann(coker \overline p)\,,\] where \( Fitt_1(coker \overline{p})\) is the first fitting ideal of \(coker \overline{p}\) and \(Ann(coker \overline{p})\) is the annihilator ideal of \(coker \overline{p}\) from which we obtain \[ Fitt_1(coker \overline{q})\subseteq Ann(coker \overline q)\subseteq Ann(coker \overline p) = Fitt_1(coker \overline{q}) \,,\] and on replacing \(coker \overline q\) by \(coker q\) we get \[ Fitt_1(coker {q})\subseteq H^0_*( Fitt_1(coker \overline{q}))\subseteq H^0_*( Fitt_1(coker \overline{p})) \,,\] since \(p\) degenerates in expected codimension \(N\), \(R\) is cohen-macaulay and \(R/ Fitt_1(coker p)\) is cohen-macaulay of dimension 1 [17] Theorem 18.18]. The irrelevant maximal ideal \(\mathscr{m}\vartriangleleft R\) is not an associated prime of \( Fitt_1(coker p)\) and is then saturated hence \[H^0_*( Fitt_1(coker \overline{p})) = Fitt_1 (coker p).\] Since now \( Fitt_1(coker p)\) is generated by polynomials of multidegree \(\geq \gamma\) no polynomial in \( Fitt_1 (coker q)\) will have multidegree less than \(\gamma\). Note that, since \(f\) is injective and \(R^{\beta}\longrightarrow W\otimes R\) is a general quotient, the map \(q:R(-1)^\alpha\longrightarrow W\otimes R\) may be assumed to be of maximal rank. If \(q\) is generally surjective we must have \begin{equation}\tag{1} \dim W\geq \gamma\,, \end{equation} otherwise \begin{equation}\tag{2} \dim W> \alpha\,. \end{equation} Since \(\dim W = \beta-\dim U\) and \(\dim U = \gamma+N-1\) then equation 1 yields \(\beta\geq 2\gamma+N-1\) and equation 2 yields \(\beta\geq \alpha+\gamma+N\).

Remark 1.

1. The first part of the theorem is a consequence of Theorem 3.3 [9], however the theorem above is an if and only if case.
2. The converse part of the theorem follows Marchesi et al., [7].
3. For certain values of \(\alpha,\beta\) and \(\gamma\) in the above monad the cohomology bundle is simple.

We now set up for monads on the Cartesian product \(X = \mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\).

Lemma 4. Let \(n,m\) and \(k\) are positive integers, given four matrices \(f_1,f_2,f_3\) and \(f_4\) of order \(k\) by \(n+k\), and four other matrices \(g_1,g_2,g_3\) and \(g_4\) of order \(n+k\) by \(k\) as shown; \begin{align*} f_1 &=\left[ \begin{array}{ccccc} &y_n \cdots y_0 \\ ⋰ & ⋰ \\ y_n \cdots y_0 \end{array} \right]_{k\times {(n+k)}},\\ f_2 &=\left[ \begin{array}{ccccccc} &x_n \cdots x_0\\ ⋰ & ⋰\\ x_n \cdots x_0 \end{array} \right]_{k\times {(n+k)}},\\ f_3 &=\left[ \begin{array}{ccccccc} &t_m \cdots t_0\\ ⋰ & ⋰ \\ t_m \cdots t_0 \end{array} \right]_{k\times {(m+k)}},\end{align*} \begin{align*} f_4 &=\left[ \begin{array}{ccccccc} &z_m \cdots z_0\\ ⋰ & ⋰ \\ z_m \cdots z_0 \end{array} \right]_{k\times {(m+k)}},\\ g_1 &=\left[\begin{array}{cccccc} x_0\\ \vdots &\ddots & x_0\\ x_n &\ddots &\vdots\\ && x_n \end{array} \right]_{{(n+k)}\times k},\\ g_2 &=\left[\begin{array}{cccccc} y_0\\ \vdots &\ddots & y_0\\ y_n &\ddots &\vdots\\ && y_n \end{array} \right]_{{(n+k)}\times k},\\ g_3 &=\left[ \begin{array}{cccccc} z_0\\ \vdots &\ddots & z_0\\ z_m &\ddots &\vdots\\ && z_m \end{array} \right]_{{(m+k)}\times k}\end{align*} and \[ g_4 =\left[\begin{array}{cccccc} t_0\\ \vdots &\ddots & t_0\\ t_m &\ddots &\vdots\\ && t_m \end{array} \right]_{{(m+k)}\times k}\,,\] we define two matrices \(f\) and \(g\) as follows; \[ f =\left[\begin{array}{cccc} f_1 & -f_2 & f_3 & -f_4 \end{array} \right]\] and \[ g =\left[\begin{array}{cc} g_1 \\ g_2 \\g_3 \\ g_4 \end{array} \right].\] Then we have

1. \(f\cdot g = 0\), and
2. The matrices \(f\) and \(g\) have maximal rank.

Proof.

1. Since \(f_1\cdot g_1 = f_2\cdot g_2\), \(f_3\cdot g_3 = f_4\cdot g_4\) then we have that \[ f\cdot g =\left[ \begin{array}{cccc} f_1 & -f_2 & f_3 & -f_4 \end{array} \right] \left[ \begin{array}{cc} g_1 \\ g_2 \\ g_3 \\ g_4\end{array} \right] =[f_1g_1 - f_2g_2 - f_3g_3 - f_4g_4] =[0]\,.\]
2. Notice that the rank of the two matrices drops if and only if all \(x_0,...,x_n\), \(y_0,...,y_n\), \(z_0,...,z_m\) and \(t_0,...,t_m\) are zeros and this is not possible in a projective space. Hence maximal rank.

Using the matrices given in the above lemma we are going to construct a monad.

Theorem 5. Let \(n,m\) and \(k\) be positive integers. Then there exists a linear monad on \(X = \mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\) of the form; \[ 0\rightarrow {\mathcal{O}_X(-1,-1,-1,-1)^{\oplus k}} \underrightarrow{f}{\mathscr{G}_n\oplus \mathscr{G}_m}\underrightarrow{g}\mathcal{O}_X(1,1,1,1)^{\oplus k} \rightarrow 0\,, \] where \(\mathscr{G}_n:=\mathcal{O}_X(0,-1,0,0)^{\oplus n+k}\oplus\mathcal{O}_X(-1,0,0,0)^{\oplus n+k}\) and \(\mathscr{G}_m:=\mathcal{O}_X(0,0,-1,0)^{\oplus m+k}\oplus\mathcal{O}_X(0,0,0,-1)^{\oplus m+k}\).

Proof. The maps \(f\) and \(g\) in the monad are the matrices given in Lemma 4. Notice that \[f\in \text{Hom}(\mathcal{O}_X(-1,-1,-1,-1)^{\oplus k},\mathscr{G}_n\oplus\mathscr{G}_m)\quad \text{ and} \quad g\in\text{Hom}(\mathscr{G}_n\oplus\mathscr{G}_m,\mathcal{O}_X(1,1,1,1)^{\oplus k}).\] Hence by the above lemma they define the desired monad.

Theorem 6. Let \(T\) be a vector bundle on \(X=\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\) defined by the sequence \[0\rightarrow T \rightarrow \mathscr{G}_n\oplus\mathscr{G}_m\underrightarrow{g}\mathcal{O}_X(1,1,1,1)^{\oplus k} \rightarrow 0\,,\] where \(\mathscr{G}_n:=\mathcal{O}_X(0,-1,0,0)^{\oplus n+k}\oplus\mathcal{O}_X(-1,0,0,0)^{\oplus n+k}\) and \(\mathscr{G}_m:=\mathcal{O}_X(0,0,-1,0)^{\oplus m+k}\oplus\mathcal{O}_X(0,0,0,-1)^{\oplus m+k}\), then \(T\) is stable for an ample line bundle \(\mathscr{L} = \mathcal{O}_X(1,1,1,1)\).

Proof. We need to show that \(H^0(X,\bigwedge^q T(-p_1,-p_2,-p_3,-p_4))=0\) for all \(\displaystyle{\sum_{i=1}^4p_i\geq0}\) and \(1\leq q\leq rank(T)\). Consider the ample line bundle \(\mathscr{L} = \mathcal{O}_X(1,1,1,1) = \mathcal{O}(L)\). Its class in \( pic(X)= \langle [a\times\mathbf{P}^n],[\mathbf{P}^n\times b],[c\times\mathbf{P}^n],[\mathbf{P}^n\times d]\rangle\) corresponds to the class \[1\cdot[a\times\mathbf{P}^n]+1\cdot[\mathbf{P}^n\times b]\cdot[c\times\mathbf{P}^m]+1\cdot[\mathbf{P}^m\times d],\] where \(a\) and \(b\) are hyperplanes of \(\mathbf{P}^n\) and \(c\) and \(d\) hyperplanes of \(\mathbf{P}^m\) with the intersection product induced by \(a^{n} = b^{n} = c^{m} = d^{m}=1\) and \(a^{n+1} = b^{n+1} = c^{n+1} = d^{n+1=0}\). Now from the display diagram of the monad, we get \begin{align*} \begin{split} c_1(T) & = c_1(\mathscr{G}_n\oplus\mathscr{G}_m) - c_1(\mathcal{O}_X(1,1,1,1)^{\oplus k})\\ & = (n+k)(-1,0,0,0)+(n+k)(0,-1,0,0)+(m+k)(0,0,-1,0)+(m+k)(0,0,0,-1) - k(1,1) \\ & = (-n-2k,-n-2k,-m-2k,-m-2k)\,. \end{split} \end{align*} Since \(L^{2n+2m}>0\) the degree of \(T\) is, \begin{align*} \deg_{\mathscr{L}}T &= c_1(T)\cdot\mathscr{L}^{d-1}\\ &=-(n+m+4k)([a\times\mathbf{P}^n]+[\mathbf{P}^n\times b]+[c\times\mathbf{P}^m]+[\mathbf{P}^m\times d])\cdot \\ &(1\cdot[a\times\mathbf{P}^n]+1\cdot[\mathbf{P}^n\times b]+1\cdot[c\times\mathbf{P}^m]+1\cdot[\mathbf{P}^m\times d])^{2n+2m-1}\\ &=-(n+m+4k)L^{2n+2m}< 0.\end{align*} Since \(\deg_{\mathscr{L}}T< 0\), then \((\bigwedge^q T)_{\mathscr{L}-norm} = (\bigwedge^q T)\) and it suffices by the generalized Hoppe Criterion (Proposition 2), to prove that \(h^0(\bigwedge^q T(-p_1,-p_2,-p_3,-p_4)) = 0\) with \(\displaystyle{\sum_{i=1}^4p_i\geq0}\) and for all \(1\leq q\leq rk(T)-1\). Next we twist the exact sequence \[0\rightarrow T \rightarrow \mathscr{G}_n\oplus\mathscr{G}_m\underrightarrow{g}\mathcal{O}_X(1,1,1,1)^{\oplus k} \rightarrow 0\] by \(\mathcal{O}_X(-p_1,-p_2,-p_3,-p_4)\) we get, \[ 0\rightarrow T(-p_1,-p_2,-p_3,-p_4)\rightarrow \mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m\rightarrow \mathcal{O}_X(1-p_1,1-p_2,1-p_3,1-p_4)^{\oplus k}\rightarrow 0\,,\] where \[\mathscr{\overline{G}}_n:=\mathcal{O}_X(-1-p_1,-p_2,-p_3,-p_4)^{\oplus n+k}\oplus\mathcal{O}_X(-p_1,-1-p_2,-p_3,-p_4)^{\oplus n+k}\] and \[\mathscr{\overline{G}}_m:=\mathcal{O}_X(-p_1,-p_2,-1-p_3,-p_4)^{\oplus m+k}\oplus\mathcal{O}_X(-p_1,-p_2,-p_3,-1-p_4)^{\oplus m+k}\] and taking the exterior powers of the sequence by Proposition 3, we get \[0\rightarrow \bigwedge^q T(-p_1,-p_2,-p_3,-p_4) \rightarrow \bigwedge^q \mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m\rightarrow \cdots\,.\] Taking cohomology we have the injection: \[0\rightarrow H^0(X,\bigwedge^{q}T(-p_1,-p_2,-p_3,-p_4))\hookrightarrow H^0(X,\bigwedge^q \mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m)\,.\] From Lemma 1 and Lemma 2, we have \(H^0(X,\bigwedge^q \mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m)=0\). implies \(h^0(X,\bigwedge^{q}T(-p_1,-p_2,-p_3,-p_4)) = h^0(X,\bigwedge^q \mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m)=0\), i.e. \(h^0(X,\bigwedge^{q}T(-p_1,-p_2,-p_3,-p_4))=0\) and thus \(T\) is stable.

Theorem 7. Let \(X=\mathbf{P}^n\times\mathbf{P}^n\times\mathbf{P}^m\times\mathbf{P}^m\), then the cohomology vector bundle \(E\) associated to the monad \[ 0\rightarrow {\mathcal{O}_X(-1,-1,-1,-1)^{\oplus k}} \underrightarrow{f}{\mathscr{G}_n\oplus\mathscr{G}_m}\underrightarrow{g}\mathcal{O}_X(1,1,1,1)^{\oplus k} \rightarrow 0 \] of rank \(2n+2m+2k\) is simple.

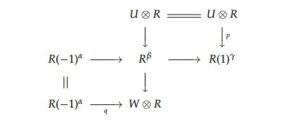
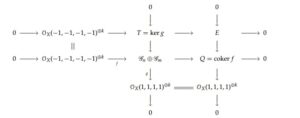
Proof. The display of the monad is

Since \(T\) is stable from theorem 3.6 above, we prove the cohomology bundle \(E\) is simple. The first step is to take the dual of the short exact sequence \[ 0\rightarrow \mathcal{O}_X(-1,-1,-1,-1)^{\oplus k} \rightarrow T\rightarrow E \rightarrow 0 \] to get \[ 0\rightarrow E^* \rightarrow T^* \rightarrow \mathcal{O}_X(1,1,1,1)^{\oplus k}\rightarrow 0. \] Tensoring by \(E\) we get \[ 0\rightarrow E\otimes E^* \rightarrow E\otimes T^* \rightarrow E(1,1,1,1)^k\rightarrow 0. \] Now taking cohomology gives: \[ 0\rightarrow H^0(X,E\otimes E^*) \rightarrow H^0(X,E\otimes T^*) \rightarrow H^0(E(1,1,1,1)^{\oplus k})\rightarrow \cdots\,, \] which implies that \begin{equation}\label{eq3}\tag{3} h^0(X,E\otimes E^*) \leq h^0(X,E\otimes T^*)\,. \end{equation} Now we dualize the short exact sequence \[ 0\rightarrow T \rightarrow {\mathscr{G}_n\oplus\mathscr{G}_m} \rightarrow \mathcal{O}_X(1,1,1,1)^{\oplus k} \rightarrow 0 \,,\] to get \[ 0\rightarrow \mathcal{O}_X(-1,-1,-1,-1)^{\oplus k} \rightarrow {\mathscr{G}_n\oplus\mathscr{G}_m} \rightarrow T^* \rightarrow 0 \,.\] For the sake of brevity we shall use the notation \(H^q(\mathscr{F})\) in place of \(H^q(X,\mathscr{F})\). Now twisting by \(\mathcal{O}_X(-1,-1,-1,-1)\) and taking cohomology and get \[ 0\rightarrow H^0(\mathcal{O}_X(-2,-2,-2,-2)^k) \rightarrow H^0(\mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m)\rightarrow H^0(T^*(-1,-1,-1,-1))\rightarrow H^1(\mathcal{O}_X(-2,-2,-2,-2)^k)\rightarrow \] \[\rightarrow H^1(\mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m)\rightarrow H^1(T^*(-1,-1,-1,-1))\rightarrow H^2(X,\mathcal{O}_X(-2,-2,-2,-2)^k) \rightarrow H^2(\mathscr{\overline{G}}_n\oplus\mathscr{\overline{G}}_m)\rightarrow \] \[\rightarrow H^2(T^*(-1,-1,-1,-1))\rightarrow \cdots \] from which we deduce \(H^0(X,T^*(-1,-1,-1,-1)) = 0\) and \(H^1(X,T^*(-1,-1,-1,-1)) = 0\) from Theorems 2 and 3. Lastly, tensor the short exact sequence \[ 0\rightarrow \mathcal{O}(-1,-1,-1,-1)^{\oplus k} \rightarrow T \rightarrow E\rightarrow 0\,, \] by \(T^*\) to get \[ 0\rightarrow T^*(-1,-1,-1,-1)^k \rightarrow T\otimes T^* \rightarrow E\otimes T^*\rightarrow 0\,, \] and taking cohomology we have \[ 0\rightarrow H^0(X,T^*(-1,-1,-1,-1)^k) \rightarrow H^0(X,T\otimes T^*) \rightarrow H^0(X,E\otimes T^*)\rightarrow \\ \rightarrow H^1(X,T^*(-1,-1,-1,-1)^k)\rightarrow \cdots\,. \] But \(H^1(X,T^*(-1,-1,-1,-1)^k=0\) for \(k>1\) from above, so we have \[ 0\rightarrow H^0(X,T^*(-1,-1,-1,-1)^{k}) \rightarrow H^0(X,T\otimes T^*) \rightarrow H^0(X,E\otimes T^*)\rightarrow 0 \,. \] This implies that \begin{equation}\label{eq4}\tag{4} h^0(X,T\otimes T^*) \leq h^0(X,E\otimes T^*)\,. \end{equation} Since \(T\) is stable then it follows that it is simple which implies \(h^0(X,T\otimes T^*)=1\). From (\ref{eq3}) and (\ref{eq4}) and putting these together we have; \[1\leq h^0(X,E\otimes E^*) \leq h^0(X,E\otimes T^*) = h^0(X,T\otimes T^*) = 1\,.\] We have \( h^0(X,E\otimes E^*) = 1 \) and therefore \(E\) is simple.

Example 1. We construct a monad on \(X = \mathbf{P}^1\times\mathbf{P}^1\times\mathbf{P}^2\times\mathbf{P}^2\) by explicitly giving the maps \(f\) and \(g\). We define \(f\) and \(g\) as follows: \[ f :=\left( \begin{array}{cccc|cccc|ccccc|ccccc} 0 & 0 & y_1 & y_0 & 0 & 0 & -x_1 & -x_0 & 0 & 0 & t_2 & t_1 & t_0 & 0 & 0 & -z_2 & -z_1 & -z_0\\ 0 & y_1 & y_0 & 0 & 0 & -x_1 & -x_0 & 0 & t_2 & t_1 & t_0 & 0 & 0 & 0 & -z_2 & -z_1 & -z_0 & 0\\ y_1 & y_0 & 0 & 0 & -x_1 & -x_0 & 0 & 0 & t_2 & t_1 & t_0 & 0 & 0 & -z_2 & -z_1 & -z_0 & 0 & 0\\ \end{array} \right) \] and \[ g :=\left( \begin{array}{ccc} x_0 & 0 & 0 \\ x_1 & x_0 & 0 \\ 0 & x_1 & x_0 \\ 0 & 0 & x_1 \\ \hline y_0 & 0 & 0 \\ y_1 & y_0 & 0 \\ 0 & y_1 & y_0 \\ 0 & 0 & y_1 \\ \hline z_0 & 0 & 0 \\ z_1 & z_0 & 0 \\ z_2 & z_1 & z_0 \\ 0 & z_2 & z_1 \\ 0 & 0 & z_2 \\ \hline t_0 & 0 & 0 \\ t_1 & t_0 & 0 \\ t_2 & t_1 & t_0 \\ 0 & t_2 & t_1 \\ 0 & 0 & t_2 \\ \end{array} \right) \,,\] from \(f\) and \(g\) we have the monad \[ 0\rightarrow {\mathcal{O}_X(-1,-1,-1,-1)^{\oplus3}} \underrightarrow{f}{\mathscr{G}_n\oplus \mathscr{G}_m}\underrightarrow{g}\mathcal{O}_X(1,1,1,1)^{\oplus3} \rightarrow 0\,, \] where \(\mathscr{G}_n:=\mathcal{O}_X(0,-1,0,0)^{\oplus4}\oplus\mathcal{O}_X(-1,0,0,0)^{\oplus4}\) and \(\mathscr{G}_m:=\mathcal{O}_X(0,0,-1,0)^{\oplus5}\oplus\mathcal{O}_X(0,0,0,-1)^{\oplus5}\).

Acknowledgment

Sincere thanks go to the Department of Mathematics, College of Science, Sultan Qaboos University for providing a conducive enviroment to be able to carry out research despite the overwhelming duties in teaching and community service. I would also wish to express my sincere thanks to the Department of Mathematics, the Catholic University of Eastern Africa for making easy for me to carry out my research work. Gratitude goes to the Department of Mathematics, the University of Nairobi for granting me leave in order to pursue my research work. Lastly, I am extremely grateful to my wife and our 3 kids who are always supportive of my pursuits.

Author Contributions:

All authors contributed equally in this paper. All authors read and approved the final version of this paper.

Conflicts of Interest:

The authors declare no conflict of interest.