Block procedure for solving stiff initial value problems using probabilists Hermite polynomials

1. Introduction

This study considers the general first order stiff initial value problems of ordinary differential equations of the form

The problem of stiffness in most ordinary differential equations (ODEs) has posed a lot of computational difficulties in many practical application modeled by ODEs. A very important special class of differential equations taken up in the initial value problems termed as stiff differential equations result from the phenomenon with widely differing time scales [2,3]. There is no universally acceptable definition of stiffness. Stiffness is a subtle, difficult and important concept in the numerical solution of ordinary differential equations. It depends on the differential equation, the initial condition and the interval under consideration. The initial value problems with stiff ordinary differential equations occur in many field of engineering science, particularly in the studies of electrical circuits, vibrations, chemical reactions and so on. Stiff differential equations are ubiquitous in astrochemical kinetics, many non-industrial areas like weather prediction and biology. A set of differential equations is `stiff' when an excessively small step is needed to obtain correct integration.

Linear multistep methods (LMMs) are very popular for solving first-order initial value problems (IVPS). LMMs are not self-starting hence, need starting values from single-step methods like Euler's method and Runge-Kutta family of methods. The general k-step method or LMM of step number \(k\) is given by Lambert [4] as follows

where the coefficients \(\alpha_{j}\)'s and \(\beta_{j}\) 's are real constants. The LMM in Equation (2) generates discrete schemes which are used to solve first-order ordinary differential equations.

The techniques for the derivation of continuous LMMs for direct solution of initial value problems in ordinary differential equations have been discussed in literature over the years and these include, among others collocation, interpolation, integration, and interpolation polynomials. Basis functions such as, power series, Chebyshev polynomials, trigonometric functions, monomials, the canonical polynomial of the Lanczos Tau method in a perturbed collocation approach have been employed for this purpose [1,5,6,7,8].

Berhan et al. [1] constructed block procedure with implicit sixth order linear multistep method using Legender polynomial for solving stiff initial value problems. In this study, we constructed implicit linear multistep method in block form of uniform step size for the solution of stiff first order ordinary differential equation using probabilists Hermite polynomial as a base function. The procedure yields four linear multistep schemes which are combined as simultaneous numerical integrators to form block method. The method is found to be consistent and zero-stable and hence convergent. Briefly, the present method is stable, accurate and effective method for solving stiff first order differential equations.

2. Description of the method

2.1. Derivation of the linear multistep methods

In [9,10], some continuous LMM of the type in Equation (3) were developed using the collocation function of the form: Awoyemi et al. [11] proposed a similar function to Equation (3) as to develop LMM for the solution of third-order IVPs. Adeniyi and Alabi [12] used Chebyshev polynomial function of the form: \[y(x)=\sum_{j=0}^{k}\alpha_{j}T_j\left(\frac{x-x_k}{h}\right),\] where \(T_j(x)\) are Chebyshev functions to develop continuous LMM.

In this paper, we applied the Probabilists Hermite polynomial proposed by Koornwinder et al. [13] which is given as

\[y(x)=\sum_{j=0}^{k}\alpha_{j}H_j(x-x_k)\], where \(H_j\) are probabilists Hermite polynomials generated by the recursive relation \[H_{n+1}(x)=xH_n(x)-H_n\prime(x), \,H_{0}=1.\] The first seven probabilists Hermite polynomials are We wish to approximate the exact solution \(y(x)\) to the IVP in Equation (1) by a polynomial of degree \(n\) of the form Hence \[y\prime(x)=f(x,y)=\sum_{j=1}^{k}a_{j}H\overset{^{\prime}}{_j}(x-x_k),~~~ x_k \leq x \leq x_{k+p}.\]

2.2. Derivation of the method for \(k=1\)

Using Equations (5) and (6), we get Differentiating Equation (7) gives Interpolating Equation (7) at \(x=x_k\) and collocating Equation (8) at \(x=x_k\) and \(x_{k+1}\), we get \begin{equation} \label{new1} \begin{cases} y(x_k)=&a_0-a_2, \nonumber \\ y\prime(x_k)=& a_1=f_k, \text{ and }\nonumber\\ y\prime(x_{k+1})=& a_1+2a_2h=f_{k+1}. \end{cases} \end{equation} The system of Equations (9) can be written in matrix form as \begin{equation*} \left( \begin{array}{ccc} 1 & 0 & -1 \\ 0 & h & 0 \\ 0 & h & -2h^{2} \end{array} \right)\left(\begin{array}{c} a_0 \\ a_1 \\ a_2 \end{array} \right)=\left(\begin{array}{ccc} y(x_k) \\ hf_k \\ hf_{k+1} \end{array} \right). \end{equation*} Solving the system of equations, we obtain \begin{eqnarray*} a_0&=&\frac{1}{2h}(f_{k+1}-f_k)+y(x_k),\\ a_1&=& f_k, \text{ and }\\ a_2&=&\frac{1}{2h^{2}}(f_{k+1}-f_k). \end{eqnarray*} Substituting \(a_j,\) for \(j=0,1,2\) in Equation (7) yields the continuous method Interpolating Equation (9) at \(x=x_{k+1}\), we obtain the discrete form

2.3. Derivation of the method for \(k=2\)

Using Equations (5) and (6), we get Differentiating Equation (11) gives Interpolating Equation (11) at \(x=x_k\) and collocating Equation (12) at \(x=x_k,x_{k+1}\), and \(x_{k+2}\), we get The matrix form of system of Equations (13) is \begin{equation*} \left( \begin{array}{cccc} 1 & 0 & -1 & 0 \\ 0 & h & 0 & -3h \\ 0 & h & 2h^{2} & 3h^{2}-3h\\ 0 & h & 4h^{2} & 12h^{3}-3h \end{array} \right)\left(\begin{array}{c} a_0 \\ a_1 \\ a_2 \\ a_3 \end{array} \right)=\left(\begin{array}{cccc} y(x_k) \\ hf_k \\ hf_{k+1}\\ hf_{k+2} \end{array} \right) \end{equation*} Solving the system of equations, we obtain \begin{eqnarray*} a_0 &=& \frac{1}{12h}(-5h^{2}f_k+8h^{2}f_{k+1}-h^{2}f_{k+2}-12y_{k+1}h+9f_k-12f_{k+1}+3f_{k+2}),\\ a_1&=&\frac{1}{h^{2}}(2h^{2}f_k+f_k-2f_{k+1}+f_{k+2}),\\ a_2&=&\frac{1}{4h}(3f_k-4k_{k+1}+f_{k+2}), \text{ and } \\ a_3 &=& \frac{1}{6h}(f_k-2f_{k+1}+f_{k+2}). \end{eqnarray*} Substituting \(a_j,\) for \(j=0,1,2,3\) in Equation (11) yields Interpolating Equation (14) at \(x=x_{k+2}\), we obtain

2.4. Derivation of the method for \(k=3\)

Using Equations (5) and (6), we get Differentiating Equation (15) gives Interpolating Equation (16) at \(x=x_{k+1}\) and collocating Equation (17) at \(x=x_k,x_{k+1},x_{k+2}\), and \(x_{k+3}\), we get The matrix form of system of Equations (18) is \begin{equation*} \left( \begin{array}{ccccc} 1 & h & h^{2}-1 & h^{3}-3h & h^{4}-6h^{2}+3\\ 0 & h & 0 & -3h & 0 \\ 0 & h & 2h^{2} & 3h^{3}-3h & 4h^{4}-12h^{2}\\ 0 & h & 4h^{2} & 12h^{3}-3h & 32h^{4}-24h^{2}\\ 0 & h & 6h^{2} & 27h^{3}-3h & 108h^{4}-36h^{2} \end{array} \right)\left(\begin{array}{c} a_0 \\ a_1 \\ a_2 \\ a_3\\ a_4 \end{array} \right)=\left(\begin{array}{ccccc} y_{k+1} \\ hf_k \\ hf_{k+1}\\ hf_{k+2}\\ hf_{k+3} \end{array} \right).\label{21} \end{equation*} Solving the system of equations, we have \begin{eqnarray} a_0 &=& \frac{1}{24h^{3}}(9h^{4f_k}+19h^{4}f_{k+1}-5h^{4}f_{k+2}+h^{4}f_{k+3}-24h^{3}y_{k+1}+22h^{2}f_k-36h^{2}f_{k+1}\nonumber\\&&{}+18h^{2}f_{k+2}-4h^{2}f_{k+3}+3f_k-9f_{k+1}+9f_{k+2}-3f_{k+3}) \nonumber\\ a_1 &=& \frac{1}{2h^{2}}(2h^{2}f_k+2f_k-5f^{k+1}+4f_{k+2}-f_{k+3})\nonumber\\ a_2 &=& \frac{1}{12h^{3}}(-11h^{2}f_k-18h^{2}f_{k+1}+9h^{2}f_{k+2}-2h^{2}f_{k+3}+3f_{k}-9f_{k+1}+9f_{k+2}-3f_{k+3})\nonumber\\ a_3 &=& \frac{1}{24h^{2}}(2f_k-5f_{k+1}+4f_{k+2}-f_{k+3})\nonumber\\ a_4&=& \frac{1}{24h^{3}}(-f_k-3f_{k+1}+3f_{k+2}-f_{k+3})\nonumber \end{eqnarray} Substituting \(a_j,\) for \(j=0,1,2,3,4\) in Equation (16) yields Interpolating Equation (19) at \(x=x_{k+3}\), we obtain the discrete form

2.5. Derivation of the method for \(k=4\)

Using Equations (5) and (6), we get Differentiating Equation (21) gives Interpolating Equation (21) at \(x=x_{k+2}\) and collocating Equation (22) at \(x=x_k,x_{k+1},x_{k+2},x_{k+3}\), and \(x_{k+4}\), we get The matrix form of system of Equations (23) is \begin{eqnarray*} \left( \begin{array}{cccccc} 1 & 2h & 4h^{2}-1 & 8h^{3}-6h & 16h^{4}-24h^{2}+3 & 32h^{5}-80h^{3}+30h\\ 0 & h & 0 & -3h & 0 & 15h \\ 0 & h & 2h^{2} & 3h^{3}-3h & 4h^{4}-12h^{2} & 5h^{5}-30h^{3}+15h \\ 0 & h & 4h^{2} & 12h^{3}-3h & 32h^{4}-24h^{2} & 80h^{5}-120h^{3}+15h\\ 0 & h & 6h^{2} & 27h^{3}-3h & 108h^{4}-36h^{2} & 405h^{5}-270h^{3}+15h\\ 0 & h & 8h^{2} & 48h^{3}-3h & 256h^{4}-48h^{2} & 1280h^{5}-480h^{3}+15h \end{array} \right)\left(\begin{array}{c} a_0 \\ a_1 \\ a_2\\ a_3 \\ a_4\\ a_5 \end{array} \right)=\left(\begin{array}{cccccc} y_{k+2} \\ hf_k \\ hf_{k+1}\\ hf_{k+2}\\ hf_{k+3}\\ hf_{k+4} \end{array} \right).\end{eqnarray*} Solving the system of equations, we have \begin{eqnarray*} a_0 &=& \frac{-1}{720h^{3}}(232h^{4}f_k+992h^{4}f_{k+1}+192h^{4}f_{k+2}+32h^{4}f_{k+3}-8h^{4}f_{k+4}-720h^{3}y_{k+2}\\ &&+750h^{2}f_k-1440h^{2}f_{k+1}+1080h^{2}f_{n+2}-480h^{2}f_{k+3}+90h^{2}f_{k+4}+225f_k-810f_{k+1}\\ &&+1080f_{k+2}-630f_{k+3}+135f_{k+4}),\\ a_1&=& \frac{1}{24h^{4}}(24h^{4}f_k+35h^{2}f_k-104h^{2}f_{k+1}114h^{2}f_{k+2}-56hf_{k+3}+11h^{2}f_{k+4}+3f_k- 12f_{k+1}\\&&+18f_{k+2}-12f_{k+3}+3f_{k+4}),\\ a_2&=&-\frac{1}{24h^{3}}(25h^{2}f_k-48h^{2}f_{k+1}+36h^{2}f_{k+2}-16h^{2}f_{k+3}3h^{2}f_{k+4}+15f_k-54f_{k+1}+72_{k+2}\\ &&-42f_{k+3}+9f_{k+4}),\\ a_3&=&\frac{1}{72h^{4}}(35h^{2}f_k-104h^{2}f_{k+1}+114h^{2}f_{k+2}-56h^{2}f_{k+2}+11h^{2}f_{k+4}+6f_k- 28f_{k+1}+36f_{k+2}\\&&-24f_{k+3}+6f_{k+4}),\\ a_4&=&-\frac{1}{48h^{3}}(5f_k-18f_{k+1}+24f_{k+2}-14f_{k+3}+3f_{k+4}), \text{ and }\\ a_5&=&\frac{1}{120h^{4}}(f_k-4f_{k+1}+6f_{k+2}-4f_{k+3}+f_{k+4}). \end{eqnarray*} Substituting \(a_j,\) for \(j=0,1,2,3,4,5\) in Equation (21) yields \( y(x)= \frac{-1}{720h^{3}}(232h^{4}f_k+992h^{4}f_{k+1}+192h^{4}f_{k+2}+32h^{4}f_{k+3}-8h^{4}f_{k+4}- 720h^{3}y_{k+2}+750h^{2}f_k-1440h^{2}f_{k+1}+1080h^{2}f_{n+2}-480h^{2}f_{k+3}+ 90h^{2}f_{k+4}-810f_{k+1}+1080f_{k+2}-630f_{k+3}+135f_{k+4})+\frac{1}{24h^{4}}(24h^{4} f_k+ 35h^{2}f_k-104h^{2}f_{k+1}114h^{2}f_{k+2}-56hf_{k+3}+11h^{2}f_{k+4}+3f_k- 12f_{k+1}+ 18f_{k+2}-12f_{k+3}+3f_{k+4})(x-x_k)-\frac{1}{24h^{3}}(25h^{2}f_k-16h^{2} f_{k+3}+ 3h^{2}f_{k+4}+15f_k-54f_{k+1}-104h^{2}f_{k+1}+114h^{2}f_{k+2}+ 72f_{k+2} -42f_{k+3} +9f_{k+4})[(x-x_k)^{2}-1]+\frac{1}{72h^{4}}(35h^{2}f_k-56h^{2}f_{k+2}-28f_{k+1} +36f_{k+2}-24f_{k+3}+6f_{k+4})+\frac{1}{48h^{3}}(5f_k-18f_{k+1}+24f_{k+2}-14f_{k+3} +3f_{k+4})[(x-x_k)^{4}-6(x-x_k)^{2}+3]+\frac{1}{120h^{4}}(f_k-4f_{k+1}+6f_{k+2} -4f_{k+3}+f_{k+4})-10(x-x_k)^{3}+15(x-x_k)].\) Interpolating Equation (24) at \(x=x_{k+4}\), we obtain

2.6. The proposed block method

The proposed block procedure with implicit linear multistep method is given by

3. Analysis of the method

3.1. Order and error constant

It is convenient at this point to introduce the so called characteristic polynomials \[\rho(z)=\sum_{j=0}^{k}\alpha_{j}z^{j}\] and \[\sigma(z)=\sum_{j=0}^{k}\beta_{j}z^{j}\] for the linear multistep methods given in Equation (2) obtained by using the substitutions \(y_{n+j}=z^{j}\) and \(f_{n+j}=\lambda\) \(z^{j}\) where \(z\) is a variable and \(j=0,1,2,3,\cdots,k\). Moreover, following Henric [14], the approach adopted in Fatunla [15], Lambert [16], and Suli and Mayer [17], they define the local truncation error associated with Equation (26) by the difference operator where \(y(x)\) is the exact solution. Assuming \(y(x)\) is smooth and expanding Equation (27) in Taylor series give us and According to Lambert [16], any linear multistep method of the form Equation (2) is of order p if \(c_0=c_1=c_2=\) \(\ldots\) \(c_p=0\) and \(c_{p+1}\neq0.\) In this case the number \(\frac{c_{p+1}}{\sigma(1)}\) is called the error constant of the method. Thus, the order of Equation (26) is \((2~3~4~5)^{T}\) with error constant \((-0.833333~-0.83333~-0.011~-0.011)^{T}\).

3.2. Zero stability of the method

Definition 1. [18] A block method is zero-stable provided that the root \( z_{j},j=1(1)k \) of the first characteristics polynomial satisfies \(|z_{j}|\leq1\) and for those root with \(|z_{j}|\) the multiplicity must not exceed two.

The characteristic polynomials of Equations (10),(15),(20) and (25) are \(z-1=0, z^{2}-z=0, z^{3}-z^2=0\) and \(z^4-z^3=0\) respectively. Hence, they are all zero stable according to Definition 1.

3.3. Consistency of the method

Definition 2. [16] A linear multistep method is said to be consistent if it has order at least one.

Using Definition 2, the linear method is said to be consistent if it has an order greater than or equal to one. Therefore, the block method (26) is consistent, since the orders of each method is greater than one.

3.4. Convergence of the method

Theorem 3.[19] A necessary and sufficient condition for a linear multistep method to be convergent is that it be consistent and zero-stable.

The proposed method satisfies the two conditions stated in Definition 1 and Definition 2. Hence, according to Theorem 1 the scheme in Equation (26) is convergent.

4. Numerical examples

The mode of implementation of our method is by combining the schemes Equation (26) as a block for solving Equation (1). It is a simultaneous integrator without requiring the starting values. To assess the performance of the proposed block method, we consider two stiff first order initial value problems in ODEs. The maximum absolute errors of the proposed method is compared with that of Runge Kutta order 4 (RK4) and Berhan et al. [1]. All calculations are carried out with the aid of MATLAB software.

Example 1.[18] Consider the first order stiff ordinary differential equation \[y\prime=-1000(y-x^{3})+3x^{2},~~y(0)=0,~~x\in[0,1]\]. The exact solution is \(y(x)=x^{3}\). Maximum Absolute errors of RK4 and the present method is given in Table 1

Table 1. Maximum Absolute errors of RK4 and the present Method for Example 1.

h	RK4	Present method
\(10^{-1}\)	\(2.81614e+60\)	\(1.78054e-04\)
\(10^{-2}\)	\(1.07457e+239\)	\(3.67265e-07\)
\(10^{-3}\)	\(9.98899e-08\)	\(5.00000e-10\)
\(10^{-4}\)	\(6.5319e-12\)	\(5.00033e-12\)
\(10^{-5}\)	\(2.88657e-15\)	\(5.11812e-14\)

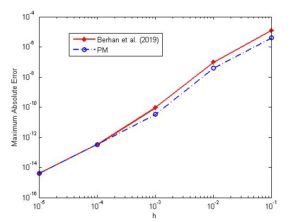
Example 2.[20] Consider the first order stiff ordinary differential equation \[y\prime=-2100\Bigl(y-cos(x)\Bigr)-sin(x),~~~y(0)\in[0,1].\] The exact solution is \(y(x)=cos(x).\) Maximum Absolute error of Berhan et al. [1] and the present method in Table 2.

Table 2. Maximum Absolute errors of Berhan \textit{ et al.} \cite{1} and the present Method for Example 2.

h	Berhan \textit{et al.} [8]	Present method
\(10^{-1}\)	\(1.22516e-5\)	\(4.06068e-06\)
\(10^{-2}\)	\(9.67880e-8\)	\(3.78971e-8\)
\(10^{-3}\)	\(6.46040e-11\)	\(3.3317e-11\)
\(10^{-4}\)	\(3.33844e-13\)	\(3.33844e-13\)
\(10^{-5}\)	\(4.10783e-15\)	\(4.10782e-15\)

5. Concluding remarks

This paper presented a block procedure with the linear multistep method based on probabilists' Hermite polynomials for solving first order IVPs in ODEs. A collocation approach along with interpolation at some grid points which produces a family block scheme with maximum order five has been proposed for the numerical solution of stiff problems in ODEs. The method is tested and found to be consistent, zero stable and convergent. We implement the method on two numerical examples, and the numerical evidence shows that the method is accurate and effective for stiff problems.

Acknowledgments

The authors would like to thank the College of Natural Sciences, Jimma University for funding this research work.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflict of Interests

The authors declare no conflict of interest.