Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2020.0033
Reinterpreting the middle-levels theorem via natural enumeration of ordered trees
Italo Jose Dejter
Department of Mathematics, University of Puerto Rico, San Juan, Puerto Rico.; italo.dejter@gmail.com
Abstract
Keywords:
1. Introduction
Let \(0< k\in\mathbb{Z}\). The middle-levels graph \(M_k\) [1] is the subgraph induced by the \(k\)-th and \((k+1)\)-th levels (formed by the \(k\)- and \((k+1)\)-subsets of \([2k+1]=\{0,\ldots,2k\}\)) in the Hasse diagram [2] of the Boolean lattice \(2^{[2k+1]}\). The dihedral group \(D_{4k+2}\) acts on \(M_k\) via translations mod \(2k+1\) (Section 4) and complemented reversals (Section 5). The sequence \(\mathcal S\) [3] {A239903} of restricted-growth strings or RGS's ([4] page 325, [5] page 224 item (u)) will be shown to unify the presentation of all \(M_k\)'s. In fact, the first \(C_k\) terms of \(\mathcal S\) will stand for the orbits of \(V(M_k)\) under natural \(D_{4k+2}\)-action, where \(C_k=\frac{(2k)!}{k!(k+1)!}\) is the \(k\)-th Catalan number [3] {A000108}. This will provide a reinterpretation (Section 10) of the Middle-Levels Theorem on the existence of Hamilton cycles in \(M_k\) [6, 7], via \(k\) -germs (Section 2) of RGS's. For the history of this theorem, [6] may be consulted, but the conjecture answered by it was learned from B. Bollob\'as on January 23, 1983, who mentioned it as a P. Erdős conjecture.
In Section 6, the cited \(D_{4k+2}\)-action on \(M_k=(V(M_k),E(M_k))\) allows to project \(M_k\) onto a quotient graph \(R_k\) whose vertices stand for the first \(C_k\) terms of \(\mathcal S\) via the lexical-matching colors [1] (or lexical colors) \(0,1,\ldots,k\) on the \(k+1\) edges incident to each vertex (Section 12). In preparation, RGS's \(\alpha\) are converted in Section 3 into \((2k+1)\)-strings \(F(\alpha)\), composed by the \(k+1\) lexical colors and \(k\) asterisks, representing all ordered (rooted) \(k\)-edge trees (Remark 1) via a ``Castling'' procedure that facilitates enumeration. These trees (encoded as \(F(\alpha)\)) are shown to represent the vertices of \(R_k\) via ``Uncastling'' procedure (Section 8).
In Section 9, the 2-factor \(W_{01}^k\) of \(R_k\) determined by the colors 0 and 1 is analyzed from the RGS-dihedral action viewpoint. From this, \(W_{01}^k\) is seen in Section 10 to morph into Hamilton cycles of \(M_k\) via symmetric differences with 6-cycles whose presentation is alternate to that of [7]. In particular, an integer sequence \({\mathcal S}_0\) is shown to exist such that, for each integer \(k>0\), the neighbors via color \(k\) of the RGS's in \(R_k\) ordered as in \(\mathcal S\) correspond to an idempotent permutation on the first \(C_k\) terms of \({\mathcal S}_0\). This and related properties hold for colors \(0,1,\ldots,k\) (Theorem 10 and Remarks 2-4) in part reflecting and extending from Observation 2 in Section 9 properties of plane trees (i.e., classes of ordered trees under root rotation). Moreover, Section 11 considers suggestive symmetry properties by reversing the designation of the roots in the ordered trees so that each lexical-color \(i\) adjacency (\(0\le i\le k\)) can be seen from the lexical-color \((k-i)\) viewpoint.
2. Restricted-Growth Strings and \(k\)-Germs
Let \(0< k\in\mathbb{Z}\). The sequence of (pairwise different) RGS's \({\mathcal S}=(\beta(0),\ldots,\beta(17),\ldots)=(0,1,10,11,12,100,101,110,111,112,120,121,122,123,1000,1001,1010,1011,\ldots)\) has the lengths of its contiguous pairs \((\beta(i-1),\beta(i))\) constant unless \(i=C_k\) for \(0< k\in\mathbb{Z}\), in which case \(\beta(i-1)=\beta(C_k-1)=12\cdots k\) and \(\beta(i)=\beta(C_k)=10^k=10\cdots 0\).
To view the continuation of the sequence \(\mathcal S\), each RGS \(\beta=\beta(m)\) will be transformed, for every \(k\in\mathbb{Z}\) such that \(k\ge\) length\((\beta)\), into a \((k-1)\)-string \(\alpha=a_{k-1}a_{k-2}\cdots a_2a_1\) by prefixing \(k-\) length\((\beta)\) zeros to \(\beta\). We say such \(\alpha\) is a \(k\)- germ. More generally, a \(k\)- germ \(\alpha\) (\(1< k\in\mathbb{Z}\)) is formally defined to be a \((k-1)\)-string \(\alpha=a_{k-1}a_{k-2}\cdots a_2a_1\) such that:
- (1) the leftmost position (called position \(k-1\)) of \(\alpha\) contains the entry \(a_{k-1}\in\{0,1\}\);
- (2) given \(1 < i< k \), the entry \(a_{i-1}\) (at position \(i-1\)) satisfies \(0\le a_{i-1}\le a_i+1\).
- (i) \(a_{k-1} < b_{k-1}\) or
- (ii) \(a_j=b_j\), for \(k-1\le j\le i+1\), and \(a_i < b_i\), for some \(k-1>i\ge 1\).
3. Castling of ordered trees
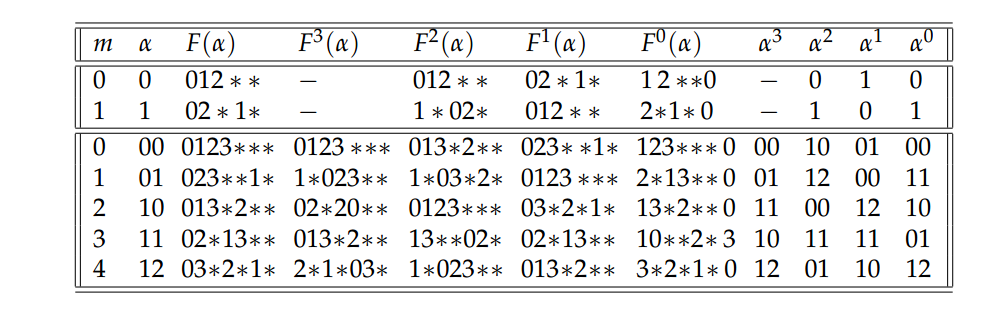
Table 1. The Castling Procedure for \(k=2,3,4\).
| \(m\) | \(\alpha\) | \(\beta\) | \(F(\beta)\) | \(i\) | \(W^i\,|\,X\,|\,Y\,|\,Z^i\) | \(W^i\,|\,Y\,|\,X\,|\,Z^i\) | \(F(\alpha)\) | \(\alpha\) |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | - | - | - | - | - | 012** | 0 |
| 1 | 1 | 0 | 012** | 1 | 0\,|\,1\,|\,2*|* | 0|2*|1|* | 02*1* | 1 |
| 0 | 00 | - | - | - | - | - | 012\,3**\,* | 00 |
| 1 | 01 | 00 | 0123*** | 1 | 0|1|23**|* | 0|23**|1|* | 023**1* | 01 |
| 2 | 10 | 00 | 0123*** | 2 | 01|2|3*|** | 01|3*|2|** | 013*2** | 10 |
| 3 | 11 | 10 | 013*2** | 1 | 0|13*|2*|* | 0|2*|13*|* | 02*13** | 11 |
| 4 | 12 | 11 | 02*13** | 1 | 0|2*1|3*|* | 0|3*|2*3|* | 03*2*1* | 12 |
| 0 | 000 | - | - | - | - | - | 01234**** | 000 |
| 1 | 001 | 000 | 01234**** | 1 | 0|1|234***|* | 0|234***|1|* | 0234***1* | 001 |
| 2 | 010 | 000 | 01234**** | 2 | 01|2|34**|** | 01|34**|2|** | 0134**2** | 010 |
| 3 | 011 | 010 | 0134**2** | 1 | 0|134**|2*|* | 0|2*|134**|* | 02*134*** | 011 |
| 4 | 012 | 011 | 02*134*** | 1 | 0|2*1|34**|* | 0|34**|2*1|* | 034**2*1* | 012 |
| 5 | 100 | 000 | 01234**** | 3 | 012|3|4*|*** | 012|4*|3|*** | 0124*3*** | 100 |
| 6 | 101 | 100 | 0124*3*** | 1 | 0|1|24*3**|* | 0|24*3**|1|* | 024*3**1* | 101 |
| 7 | 110 | 100 | 0124*3*** | 2 | 01|24*|3*|** | 01|3*|24*|** | 013*24*** | 110 |
| 8 | 111 | 110 | 013*24*** | 1 | 0|13*|24**|* | 0|24**|13*|* | 024**13** | 111 |
| 9 | 112 | 111 | 024**13** | 1 | 0|24**1|3*|* | 0|3*|24**1|* | 03*24**1* | 112 |
| 10 | 120 | 110 | 013*24*** | 2 | 01|3*2|4*|** | 01|4*|3*2|** | 014*3*2** | 120 |
| 11 | 121 | 120 | 014*3*2** | 1 | 0|14*3*|2*|* | 0|2*|14*3*|* | 02*14*3** | 121 |
| 12 | 122 | 121 | 02*14*3** | 1 | 0|2*34*|3*|* | 0|3*|2*14*|* | 03*2*14** | 122 |
| 13 | 123 | 122 | 03*2*14** | 1 | 0|3*2*1|4*|* | 0|4*|3*2*1|* | 04*3*2*1* | 123 |
Theorem 1. To each \(k\)-germ \(\alpha=a_{k-1}\cdots a_1\ne 0^{k-1}\) with rightmost entry \(a_i\ne 0\) (\(k>i\ge 1\)) corresponds a \(k\)-germ \(\beta(\alpha)=b_{k-1}\cdots b_1\!< \alpha\) with \(b_i= a_i-1\) and \(a_j=b_j\), (\(j\ne i\)). All \(k\)-germs form an ordered tree \({\mathcal T}_k\) rooted at \(0^{k-1}\), each \(k\)-germ \(\alpha\ne0^{k-1}\) with \(\beta(\alpha)\) as parent.
Proof. The statement, illustrated for \(k=2,3,4\) by means of the first 3 columns of Table 1, is straightforward. Table 1 also serves as illustration to the proof of Theorem 2, below.
By representing \({\mathcal T}_k\) with each node \(\beta\) having its children \(\alpha\) enclosed between parentheses following \(\beta\) and separating siblings with commas, we can write: $${\mathcal T}_4=000(001,010(011(012)),100(101,110(111(121)),120(121(122(123))))).$$Theorem 2. To each \(k\)-germ \(\alpha=a_{k-1}\cdots a_1\) corresponds a \((2k+1)\)-string \(F(\alpha)=f_0f_1\cdots f_{2k}\) whose entries are both the numbers \(0,1,\ldots,k\) (once each) and \(k\) asterisks (\(*\)) and such that:
- (A) \(F(0^{k-1})=012\cdots(k-2)(k-1)k*\cdots *\);
- (B) if \(\alpha\ne 0^{k-1}\), then \(F(\alpha)\) is obtained from \(F(\beta)=F(\beta(\alpha))=h_0h_1\cdots h_{2k}\) by means of the following ``Castling Procedure'' steps:
- let \(W^i=h_0h_1\cdots h_{i-1}=f_0f_1\cdots f_{i-1}\) and \(Z^i=h_{2k-i+1}\cdots h_{2k-1}h_{2k}=f_{2k-i+1}\cdots f_{2k-1}f_{2k}\) be respectively the initial and terminal substrings of length \(i\) in \(F(\beta)\);
- let \(\Omega>0\) be the leftmost entry of the substring \(U=F(\beta)\setminus(W^i\cup Z^i)\) and consider the concatenation \(U=X|Y\), with \(Y\) starting at entry \(\Omega+1\); then, \(F(\beta)=W^i|X|Y|Z^i\);
- set \(F(\alpha)=W^i|Y|X|Z^i\).
- (a) the leftmost entry of each \(F(\alpha)\) is \(0\); \(k*\) is a substring of \(F(\alpha)\), but \(*k\) is not;
- (b) a number to the immediate right of any \(b\in[0,k)\) in \(F(\alpha)\) is larger than \(b\);
- (c) \(W^i\) is an (ascending) number \(i\)-substring and \(Z^i\) is formed by \(i\) of the \(k\) asterisks.
Proof.
Let \(\alpha=a_{k-1}\cdots a_1\ne 0^{k-1}\) be a \(k\)-germ. In the sequence of applications of 1-3 along the path from root \(0^{k-1}\) to \(\alpha\) in \({\mathcal T}_k\), unit augmentation of \(a_i\) for larger values of \(i\), (\(0< i< k\)), must occur earlier, and then in strictly descending order of the entries \(i\) of the intermediate \(k\)-germs. As a result, the length of the inner substring \(X|Y\) is kept non-decreasing after each application. This is illustrated in Table 1, where the order of presentation of \(X\) and \(Y\) is reversed in successively decreasing steps. In the process, (a)-(c) are seen to be fulfilled.
The 3 successive subtables in Table 1 have \(C_k\) rows each, where \(C_2=2\), \(C_3=5\) and \(C_4=14\); in the subtables, the \(k\)-germs \(\alpha\) are shown both on the second and last columns via natural enumeration in the first column; the images \(F(\alpha)\) of those \(\alpha\) are on the penultimate column; the remaining columns in the table are filled, from the second row on, as follows:
- (i) \(\beta=\beta(\alpha)\), arising in Theorem 1
- (ii) \(F(\beta)\), taken from the penultimate column in the previous row;
- (iii) the length \(i\) of \(W^i\) and \(Z^i\) (\(k-1\ge i\ge 1\));
- (iv) the decomposition \(W^i|Y|X|Z^i\) of \(F(\beta)\);
- (v) the decomposition \(W^i|X|Y|Z^i\) of \(F(\alpha)\), re-concatenated in the following, penultimate, column as \(F(\alpha)\), with \(\alpha=F^{-1}(F(\alpha))\) in the last column.
Remark 1. As in the case of \({\mathcal T}_k\) in Theorem 1, an ordered (rooted) tree [7] is a tree \(T\) with:
- (a) a specified node \(v_0\) as the root of \(T\);
- (b) an embedding of \(T\) into the plane with \(v_0\) on top;
- (c) the edges between the \(j\)- and \((j+1)\)-levels of \(T\) (formed by the nodes at distance \(j\) and \((j+1)\) from \(v_0\), where \(0\le j< \) height\((T)\)) having (parent) nodes at the \(j\)-level above their children at the \((j+1)\)-level;
- (d) the children in (c) ordered in a left-to-right fashion.
- (i) the subindex \(i\) of each \(v_i\) in the \(\rightarrow\)DFS downward appearance and
- (ii) an asterisk for the edge \(e_i\) ending at each child \(v_i\) in the \(\rightarrow\)DFS upward appearance.
Table 2. Subscripted binary \(n\)-strings \(\hat{\theta}(\alpha)\) and complemented reversals via \(\aleph\) for \(k=2,3\).
| \(m\) | \(\alpha\) | \(\theta(\alpha)\) | \(\hat{\theta}(\alpha)\) | \(\hat{\aleph}(\theta(\alpha))=\aleph(\hat{\theta}(\alpha))\) | \(\aleph(\theta(\alpha))\) |
|---|---|---|---|---|---|
| 0 | 0 | 00011 | \(0_00_10_21_*1_*\) | \(0_*0_*1_21_11_0\) | 00111 |
| 1 | 1 | 00101 | \(0_00_21_*0_11_*\) | \(0_*1_10_*1_21_0\) | 01011 |
| 0 | 00 | 0000111 | \(0_00_10_20_31_*1_*1_*\) | \(0_*0_*0_*1_31_21_11_0\) | 0001111 |
| 1 | 01 | 0001101 | \(0_00_20_31_*1_*0_11_*\) | \(0_*1_10_*0_*1_31_21_0\) | 0100111 |
| 2 | 10 | 0001011 | \(0_00_10_32_*0_11_*1_*\) | \(0_*0_*1_20_*1_31_11_0\) | 0010111 |
| 3 | 11 | 0010011 | \(0_00_21_*0_10_31_*1_*\) | \(0_*0_*1_31_10_*1_21_0\) | 0011011 |
| 4 | 12 | 0010101 | \(0_00_31_*0_21_*0_11_*\) | \(0_*1_10_*1_20_*1_31_0\) | 0101011 |
4. Translations \(\mod n=2k+1\)
Let \(n=2k+1\). The \(n\)- cube graph \(H_n\) is the Hasse diagram of the Boolean lattice \(2^{[n ]}\) on the set \([n]=\{0,\ldots,n-1\}\). It is convenient to express each vertex \(v\) of \(H_n\) in 3 different equivalent ways:- (a) ordered set \(A=\{a_0,a_1,\ldots,a_{j-1}\}=a_0a_1\cdots a_{j-1}\subseteq [n]\) that \(v\) represents, (\(0< j\le n\));
- (b) characteristic binary \(n\)-vector \(B_A=(b_0,b_1,\ldots,b_{n-1})\) of ordered set \(A\) in (a) above, where \(b_i=1\) if and only if \(i\in A\), (\(i\in[n]\));
- (c) polynomial \(\epsilon_A(x)=b_0+b_1x+\cdots +b_{n-1}x^{n-1}\) associated to \(B_A\) in (b) above.
For each \(j\in[n]\), let \(L_j=\{A\subseteq[n]\mbox{ with }|A|=j\}\) be the \(j\)- level of \(H_n\). Then, \(M_k\) is the subgraph of \(H_n\) induced by \(L_k\cup L_{k+1}\), for \(1\le k\in\mathbb{Z}\). By viewing the elements of \(V(M_k)=L_k\cup L_{k+1}\) as polynomials, as in (c) above, a regular (i.e., free and transitive) translation mod \(n\) action \(\Upsilon'\) of \(\mathbb{Z}_n\) on \(V(M_k)\) is seen to exist, given by: \begin{eqnarray}\label{d3}\Upsilon':\mathbb{Z}_n\times V(M_k)\rightarrow V(M_k)\mbox{, with }\Upsilon'(i,v)=v(x)x^i\mbox{ (mod }1+x^n),\end{eqnarray} where \(v\in V(M_k)\) and \(i\in\mathbb{Z}_n\). Now, \(\Upsilon'\) yields a quotient graph \(M_k/\pi\) of \(M_k\), where \(\pi\) stands for the equivalence relation on \(V(M_k)\) given by: $$\epsilon_A(x)\pi\epsilon_{A'}(x)\Longleftrightarrow\exists\,i\in\mathbb{Z}\mbox{ with }\epsilon_{A'}(x)\equiv x^i\epsilon_A(x)\mbox{ (mod }1+x^n),$$ with \(A,A'\in V(M_k)\). This is to be used in the proofs of Theorems 4 and 8. Clearly, \(M_k/\pi\) is the graph whose vertices are the equivalence classes of \(V(M_k)\) under \(\pi\). Also, \(\pi\) induces a partition of \(E(M_k)\) into equivalence classes, to be taken as the edges of \(M_k/\pi\).
5. Complemented reversals
Let \((b_0b_1\cdots b_{n-1})\) denote the class of \(b_0b_1\cdots b_{n-1}\in L_i\) in \(L_i/\pi\). Let \(\rho_i:L_i\rightarrow L_i/\pi\) be the canonical projection given by assigning \(b_0b_1\cdots b_{n-1}\) to \((b_0b_1\cdots b_{n-1})\), for \(i\in\{k,k+1\}\). The definition of \(\aleph\) in display~(\ref{d2}) is easily extended to a bijection, again denoted \(\aleph\), from \(L_k\) onto \(L_{k+1}\). Let \(\aleph_\pi:L_k/\pi\rightarrow L_{k+1}/\pi\) be given by \(\aleph_\pi((b_0b_1\cdots b_{n-1}))=(\bar{b}_{n-1}\cdots\bar{b}_1\bar{b_0})\). Observe \(\aleph_\pi\) is a bijection. Notice the commutative identities \(\rho_{k+1}\aleph=\aleph_\pi\rho_k\) and \(\rho_k\aleph^{-1}=\aleph_\pi^{-1}\rho_{k+1}\).The following geometric representations will be handy. List vertically the vertex parts \(L_k\) and \(L_{k+1}\) of \(M_k\) (resp. \(L_k/\pi\) and \(L_{k+1}/\pi\) of \(M_k/\pi\)) so as to display a splitting of \(V(M_k)=L_k\cup L_{k+1}\) (resp. \(V(M_k)/\pi=L_k/\pi\cup L_{k+1}/\pi\)) into pairs, each pair contained in a horizontal line, the 2 composing vertices of such pair equidistant from a vertical line \(\phi\) (resp. \(\phi/\pi\), depicted through \(M_2/\pi\) on the left of Figure 1, Section 6 below). In addition, we impose that each resulting horizontal vertex pair in \(M_k\) (resp. \(M_k/\pi\)) be of the form \((B_A,\aleph(B_A))\) (resp. \(((B_A),(\aleph(B_A))=\aleph_\pi((B_A)))\)), disposed from left to right at both sides of \(\phi\). A non-horizontal edge of \(M_k/\pi\) will be said to be a skew edge.
Theorem 3. To each skew edge \(e=(B_{A})(B_{A'})\) of \(M_k/\pi\) corresponds another skew edge \(\aleph_\pi((B_{A}))\aleph^{-1}_\pi((B_{A'}))\) obtained from \(e\) by reflection on the line \(\phi/\pi\). Moreover:
- (i) the skew edges of \(M_k/\pi\) appear in pairs, with the endpoints of the edges in each pair forming 2 horizontal pairs of vertices equidistant from \(\phi/\pi\);
- (ii) each horizontal edge of \(M_k/\pi\) has multiplicity equal either to 1 or to 2.
Proof.
The skew edges \(B_{A}B_{A'}\) and \(\aleph^{-1}(B_{A'})\aleph(B_{A})\) of \(M_k\) are
reflection of each other about \(\phi\). Their endopoints form 2 horizontal pairs \((B_{A},\aleph(B_{A'}))\) and \((\aleph^{-1}(B_{A}),B_{A'})\) of vertices. Now, \(\rho_k\) and \(\rho_{k+1}\) extend together to a covering graph map \(\rho:M_k\rightarrow M_k/\pi\), since the edges accompany the
projections correspondingly, exemplified for \(k=2\) as follows:
\begin{align*}\aleph((B_A))&=\aleph((00011))\\
&=\aleph(\{00011,10001,11000,01100,00110\})\\
&=\{00111,01110,11100,11001,10011\}\\
&=(00111),\\
\aleph^{-1}((B_A'))&=\aleph^{-1}((01011))\\
&=\aleph^{-1}(\{01011,10110,10110,11010,10101\})\\
&=\{00101,10010,01001,10100,01010\}\\
&=(00101).\end{align*}
Here, the order of the elements in the image of class \((00011)\) (resp. \((01011)\)) mod \(\pi\) under \(\aleph\) (resp. \(\aleph^{-1}\)) are shown reversed, from right to left (cyclically between braces, continuing on the right once one reaches the leftmost brace). Such reversal holds for every \(k>2\):
\begin{align*}\aleph((B_A))&=\aleph((b_0\cdots b_{2k}))\\
&=\aleph(\{b_0\cdots b_{2k},\;b_{2k}\ldots b_{2k-1},\;\ldots,\;b_1\cdots
b_0\})\\
&=
\{\bar{b}_{2k}\cdots\bar{b}_0,\;\bar{b}_{2k-1}\cdots\bar{b}_{2k},\;\ldots,\;\bar{b}_1\cdots\bar{b}_0\}=\\
&(\bar{b}_{2k}\cdots\bar{b}_0),\\
\aleph^{-1}((B_A'))&=\aleph^{-1}((\bar{b}'_{2k}\cdots\bar{b}'_0))\\
&=\aleph^{-1}(\{\bar{b}'_{2k}\cdots\bar{b}'_0,\;\bar{b}'_{2k-1}\cdots\bar{b}'_{2k},\;\ldots,\;\bar{b}'_1\cdots\bar{b}'_0\})\\
&=
\{b'_0\cdots b'_{2k},\;b'_{2k}\cdots b'_{2k-1},\;\ldots,\;b'_1\cdots b'_0\}\\
&=(b'_0\cdots b'_{2k}),\end{align*}
where \((b_0\cdots b_{2k})\in L_k/\pi\) and \((b'_0\cdots b'_{2k})\in L_{k+1}/\pi\). This establishes (i).
Every horizontal edge \(v\aleph_\pi(v)\) of \(M_k/\pi\) has \(v\in L_k/\pi\) represented by \(\bar{b}_k\cdots \bar{b}_10b_1\cdots b_k\) in \(L_k\), (so \(v=(\bar{b}_k\cdots \bar{b}_10b_1\cdots b_k)\)). There are \(2^k\) such vertices in \(L_k\) and at most \(2^k\) corresponding vertices in \(L_k/\pi\). For example, \((0^{k+1}1^k)\) and \((0(01)^k)\) are endpoints in \(L_k/\pi\) of 2 horizontal edges of \(M_k/\pi\), each. To prove that this implies (ii), we have to see that there cannot be more than 2 representatives \(\bar{b}_k\cdots \bar{b}_1b_0b_1\cdots b_k\) and \(\bar{c}_k\cdots \bar{c}_1c_0c_1\cdots c_k\) of a vertex \(v\in L_k/\pi\), with \(b_0=0=c_0\). Such a \(v\) is expressible as \(v=(d_0 \cdots b_0d_{i+1}\cdots d_{j-1}c_0\cdots d_{2k})\), with \(b_0=d_i\), \(c_0=d_j\) and \(0< j-i\le k\). Let the substring \(\sigma=d_{i+1}\cdots d_{j-1}\) be said \((j-i)\)- feasible. Let us see that every \((j-i)\)-feasible substring \(\sigma\) forces in \(L_k/\pi\) only vertices \(\omega\) leading to 2 different (parallel) horizontal edges in \(M_k/\pi\) incident to \(v\). In fact, periodic continuation mod \(n\) of \(d_0\cdots d_{2k}\) both to the right of \(d_j=c_0\) with minimal cyclic substring
\(\bar{d}_{j-1}\cdots\bar{d}_{i+1}1d_{i+1}\cdots d_{j-1}0=P_r\) and to the left of \(d_i=b_0\) with minimal cyclic substring \(0d_{i+1}\cdots d_{j-1}1\bar{d}_{j-1}\cdots\bar{d}_{i+1}=P_\phi\) yields a 2-way infinite string that winds up onto a class \((d_0\cdots d_{2k})\) containing such an \(\omega\). For example, some pairs of feasible substrings \(\sigma\) and resulting vertices \(\omega\) are:
\begin{align*}(\sigma,\omega)=&(\emptyset,({ o}{ o}1)),\;\;(0,({ o}0{ o}11)),\;\;(1,({ o}1{ o})),\;\;(0^2,({ o}00{ o}111)),\;\;(01,({ o}01{ o}011)),\;\;(1^2,\,{ o}11{ o}0)),\\&(0^3,{ o}000{ o}1111)),\;\;
(010,({ o}010{ o}101101)),\;\;(01^2,({ o}011{ o})),\;\;(101,({ o}101{ o})),\;\;
(1^3,({ o}111{ o}00)),\end{align*} with `o' replacing \(b_0=0\) and \(c_0=0\),
and where \(k=\lfloor\frac{n}{2}\rfloor\) has successive values \(k=1,2,1,3,3,2,4,5,2,2,3\).
If \(\sigma\) is a feasible substring and \(\bar{\sigma}\) is its complemented reversal via \(\aleph\), then the possible symmetric substrings \(P_\phi\sigma P_r\) about \({o}\sigma{o}=0\sigma 0\) in a vertex \(v\) of \(L_k/\pi\) are in order of ascending length:
$$\begin{array}{c}
0\sigma 0,\\{\bar{\sigma}0\sigma 0\bar{\sigma},}\\
1\bar{\sigma}0\sigma 0\bar{\sigma}1,\\
{\sigma 1\bar{\sigma}0\sigma 0\bar{\sigma}1\sigma,}\\
{0\sigma 1\bar{\sigma}0\sigma 0\bar{\sigma}1\sigma 0,}\\
{\bar{\sigma}0\sigma 1\bar{\sigma}0\sigma 0\bar{\sigma}1\sigma 0\bar{\sigma},}\\
{1\bar{\sigma}0\sigma 1\bar{\sigma}0\sigma 0\bar{\sigma}1\sigma 0\bar{\sigma}1,}\\
{\cdots\cdots\cdots\cdots\cdots\cdots\cdots,}
\end{array}$$
where we use again `0' instead of `o' for the entries immediately preceding and following the shown central copy of \(\sigma\). The lateral periods of \(P_r\) and \(P_\phi\) determine each one horizontal edge at \(v\) in \(M_k/\pi\) up to returning to \(b_0\) or \(c_0\),
so no entry \(e_0=0\) of \((d_0\cdots d_{2k})\) other than \(b_0\) or
\(c_0\) happens such that \((d_0\cdots d_{2k})\) has a third representative
\(\bar{e}_k\cdots \bar{e}_10e_1\cdots e_k\) (besides \(\bar{b}_k\cdots
\bar{b}_10b_1\cdots b_k\) and \(\bar{c}_k\cdots \bar{c}_10c_1\cdots
c_k\)). Thus, those 2 horizontal edges are produced solely from the feasible
substrings \(d_{i+1}\cdots d_{j-1}\) characterized above.
6. Dihedral quotients
An involution of a graph \(G\) is a graph map \(\aleph:G\rightarrow G\) such that \(\aleph^2\) is the identity. If \(G\) has an involution, an \(\aleph\)-folding of \(G\) is a graph \(H\), possibly with loops, whose vertices \(v'\) and edges or loops \(e'\) are respectively of the form \(v'=\{v,\aleph(v)\}\) and \(e'=\{e,\aleph(e)\}\), where \(v\in V(G)\) and \(e\in E(G)\); \(e\) has endvertices \(v\) and \(\aleph(v)\) if and only if \(\{e,\aleph(e)\}\) is a loop of \(G\).Note that both maps \(\aleph:M_k\rightarrow M_k\) and \(\aleph_\pi:M_k/\pi\rightarrow M_k/\pi\) in Section 5 are involutions. Let \(\langle B_A\rangle\) denote each horizontal pair \(\{(B_A),\aleph_\pi((B_A))\}\) (as in Theorem 3) of \(M_k/\pi\), where \(|A|=k\). An \(\aleph\)-folding \(R_k\) of \(M_k/\pi\) is obtained whose vertices are the pairs \(\langle B_A\rangle\) and having:
- (1) an edge \(\langle B_A\rangle\langle B_{A'}\rangle\) per skew-edge pair \(\{(B_A)\aleph_\pi((B_{A'})),(B_{A'})\aleph_\pi((B_A))\};\)
- (2) a loop at \(\langle B_A\rangle\) per horizontal edge \((B_A)\aleph_\pi((B_A))\); because of Theorem 3, there may be up to 2 loops at each vertex of \(R_k\).
Theorem 4. \(R_k\) is a quotient graph of \(M_k\) under an action \(\Upsilon:D_{2n}\times M_k\rightarrow M_k\).
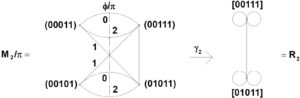
Figure 1. Reflection symmetry of \(M_2/\pi\) about a line \(\phi/\pi\) and resulting graph map \(\gamma_2\)
Proof. \(D_{2n}\) is the semidirect product \(\mathbb{Z}_n\rtimes_\varrho\mathbb{Z}_2\) via the group homomorphism \(\varrho:\mathbb{Z}_2\rightarrow\mbox{Aut}(\mathbb{Z}_n)\), where \(\varrho(0)\) is the identity and \(\varrho(1)\) is the automorphism \(i\rightarrow(n-i)\), \(\forall i\in\mathbb{Z}_n\). If \(*:D_{2n}\times D_{2n}\rightarrow D_{2n}\) indicates group multiplication and \(i_1,i_2\in\mathbb{Z}_n\), then \((i_1,0)*(i_2,j)=(i_1+i_2,j)\) and \((i_1,1)*(i_2,j)=(i_1-i_2,\bar{j})\), for \(j\in\mathbb{Z}_2\). Set \(\Upsilon((i,j),v)=\Upsilon'(i,\aleph^j(v))\), \(\forall i\in\mathbb{Z}_n, \forall j\in\mathbb{Z}_2\), where \(\Upsilon'\) is as in display (2). Then, \(\Upsilon\) is a well-defined \(D_{2n}\)-action on \(M_k\). By writing \((i,j)\cdot v=\Upsilon((i,j),v)\) and \(v=a_0\cdots a_{2k}\), we have \((i,0)\cdot v=a_{n-i+1}\cdots a_{2k}a_0\cdots a_{n-i}=v'\) and \((0,1)\cdot v'=\bar{a}_{i-1}\cdots \bar{a}_0\bar{a}_{2k}\cdots\bar{a}_i=(n-i,1)\cdot v=((0,1)*(i,0))\cdot v\), leading to the compatibility condition \(((i,j)*(i',j'))\cdot v=(i,j)\cdot ((i',j')\cdot v)\).
Theorem 4 yields a graph projection \(\gamma_k:M_k/\pi\rightarrow R_k\) for the action \(\Upsilon\), given for \(k=2\) in Figure 1. In fact, \(\gamma_2\) is associated with reflection of \(M_2/\pi\) about the dashed vertical symmetry axis \(\phi/\pi\) so that \(R_2\) (containing 2 vertices and one edge between them, with each vertex incident to 2 loops) is given as its image. Both the representations of \(M_2/\pi\) and \(R_2\) in the figure have their edges indicated with colors 0,1,2, as arising inSection 7.7. Lexical procedure
Let \(P_{k+1}\) be the subgraph of the unit-distance graph of \(\mathbb{R}\) (the real line) induced by the set \([k+1]=\{0,\ldots,k\}\). We draw the grid \(\Gamma=P_{k+1}\square P_{k+1}\) in the plane \(\mathbb{R}^2\) with a diagonal \(\partial\) traced from the lower-left vertex \((0,0)\) to the upper-right vertex \((k,k)\). For each \(v\in L_k/\pi\), there are \(k+1\) \(n\)-tuples of the form \(b_0b_1\cdots b_{n-1}=0b_1\cdots b_{n-1}\) that represent \(v\) with \(b_0=0\). For each such \(n\)-tuple, we construct a \(2k\)-path \(D\) in \(\Gamma\) from \((0,0)\) to \((k,k)\) in \(2k\) steps indexed from \(i=0\) to \(i=2k-1\). This leads to a lexical edge-coloring implicit in [1]; see the following statement and Figure 2 (Section 8), containing examples of such a \(2k\)-path \(D\) in thick trace.Theorem 5. [1] Each \(v\in L_k/\pi\) has its \(k+1\) incident edges assigned colors \(0,1,\ldots,k\) by means of the following ``Lexical Procedure'', where \(0\le i\in\mathbb{Z}\), \(w\in V(\Gamma)\) and \(D\) is a path in \(\Gamma\). Initially, let \(i=0\), \(w=(0,0)\) and \(D\) contain solely the vertex \(w\). Repeat \(2k\) times the following sequence of steps (1)-(3), and then perform once the final steps (4)-(5):
- (1) If \(b_i=0\), then set \(w':=w+(1,0)\); otherwise, set \(w':=w+(0,1)\).
- (2) Reset \(V(D):=v(D)\cup\{w'\}\), \(E(D):=E(D)\cup\{ww'\}\), \(i:=i+1\) and \(w:=w'\).
- (3) If \(w\ne(k,k)\), or equivalently, if \(i< 2k\), then go back to step (1).
- (4) Set \(\check{v}\in L_{k+1}/\pi\) to be the vertex of \(M_k/\pi\) adjacent to \(v\) and obtained from its representative \(n\)-tuple \(b_0b_1\cdots\) \(b_{n-1}=0b_1\cdots b_{n-1}\) by replacing the entry \(b_0\) by \(\bar{b}_0=1\) in \(\check{v}\), keeping the entries \(b_i\) of \(v\) unchanged in \(\check{v}\) for \(i>0\).
- (5) Set the color of the edge \(v\check{v}\) to be the number \(c\) of horizontal (alternatively, vertical) arcs of \(D\) above \(\partial\).
Proof. If addition and subtraction in \([n]\) are taken modulo \(n\) and we write \([y,x)=\{y,y+1,y+2,\ldots,x-1\}\), for \(x,y\in[n]\), and \(S^c=[n]\setminus S\), for \(S=\{i\in[n]:b_i=1\}\subseteq[n]\), then the cardinalities of the sets \(\{y\in S^c\setminus x: |[y,x)\cap S|< |[y,x)\cap S^c|\}\) yield all the edge colors, where \(x\in S^c\) varies.
The Lexical Procedure of Theorem 8 yields a 1-fac\-tor\-i\-za\-tion not only for \(M_k/\pi\) but also for \(R_k\) and \(M_k\). This is clarified by the end of Section 8.8. Uncastling and lexical 1-factorization
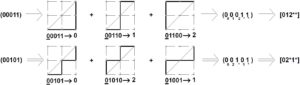
Figure 2. Representing lexical-color assignment for \(k=2\)
In each of the 2 cases in Figure 2 (top, bottom), an arrow ``\(\Rightarrow\)'' to the right of the sketches points to a modification \(\hat{v}\) of \(b_0b_1\cdots b_{n-1}=0b_1\cdots b_{n-1}\) obtained by setting as a subindex of each 0 (resp. 1) its associated color \(c\) (resp. an asterisk ``\(*\)'' ). Further to the right, a third arrow ``\(\Rightarrow\)'' points to the \(n\)-tuple \(\delta(v)\) formed by the string of subindexes of entries of \(\hat{v}\) in the order they appear from left to right.
Theorem 6. Let \(\alpha(v^0)=a_{k-1}\cdots a_1=00\cdots 0\). To each \(\delta(v)\) corresponds a sole \(k\)-germ \(\alpha=\alpha(v)\) with \(\langle F(\alpha)\rangle=\delta(v)\) by means of the following ``Uncastling Procedure'': Given \(v\in L_k/\pi\), let \(W^i=01\cdots i\) be the maximal initial numeric (i.e., colored) substring of \(\delta(v)\), so the length of \(W^i\) is \(i+1\) (\(0\le i\le k\)). If \(i=k\), let \(\alpha(v)=\alpha(v^0)\); else, set \(m=0\) and:
- set \(\delta(v^m)=\langle W^i|X|Y|Z^i\rangle\), where \( Z^i\) is the terminal \(j_m\)-substring of \(\delta(v^m)\), with \(j_m=\) \(i+1\), and let \(X,Y\) (in that order) start at contiguous numbers \(\Omega\) and \(\Omega-1\ge i\);
- set \(\delta(v^{m+1})=\langle W^i|Y|X|Z^i\rangle\);
- obtain \(\alpha(v^{m+1})\) from \(\alpha(v^m)\) by increasing its entry \(a_{j_m}\) by 1;
- if \(\delta(v^{m+1})=[01\cdots k*\cdots*]\), then stop; else, increase \(m\) by 1 and go to step 1.
Proof. This is a procedure inverse to that of Castling (Section 3), so 1-4 follow.
Theorem~\ref{un} allows to produce a finite sequence \(\delta(v^0),\delta(v^1),\ldots,\delta(v^m),\ldots,\) \(\delta(v^s)\) of \(n\)-strings with \(j_0\ge j_1\ge\cdots\ge j_m\cdots\ge j_{s-1}\) as in steps 1-4, and \(k\)-germs \(\alpha(v^0),\alpha(v^1),\ldots,\) \(\alpha(v^m),\ldots,\) \(\alpha(v^s)\), taking from \(\alpha(v^0)\) through the \(k\)-germs \(\alpha(v^m)\), (\(m=1,\ldots,s-1\)), up to \(\alpha(v)=\alpha(v^s)\) via unit incrementation of \(a_{j_m}\), for \(0\le m< s\), where each incrementation yields the corresponding \(\alpha(v^{m+1})\). Recall \(F\) is a bijection from the set \(V({\mathcal T}_k)\) of \(k\)-germs onto \(V(R_k)\), both sets being of cardinality \(C_k\). Thus, to deal with \(V(R_k)\) it is enough to deal with \(V({\mathcal T}_k)\), a fact useful in interpreting Theorem~\ref{thm4}. For example \(\delta(v^0)=\langle 04*3*2*1\,*\rangle=\langle 0|4*|3*2*1|*\rangle=\langle W^0|X|Y|Z^0\rangle\) with \(m=0\) and \(\alpha(v^0)=123\), continued in Table \ref{tab3} with \(\delta(v^1)=\langle W^0|Y|X|Z^0\rangle\), finally arriving to \(\alpha(v^s)=\alpha(v^6)=000\).Table 3. Continuation of the Uncastling Procedure started at \(\alpha(v^0)=123\).
- (I) all edges receive a common color in \([k+1]\) regardless of the endpoint on which the Lexical Procedure (or its modification immediately below) for \(v\in L_{k+1}/\pi\) is applied;
- (II) the 2 edges in each SREP in \(M_k/\pi\) are assigned a common color in \([k+1]\).
Since an SREP in \(M_k\) determines a unique edge \(\epsilon\) of \(R_k\) (and vice versa), the color received by the SREP can be attributed to \(\epsilon\), too. Clearly, each vertex of either \(M_k\) or \(M_k/\pi\) or \(R_k\) defines a bijection from its incident edges onto the color set \([k+1]\). The edges obtained via \(\aleph\) or \(\aleph_\pi\) from these edges have the same corresponding colors.
Theorem 7. A 1-factorization of \(M_k/\pi\) by the colors \(0,1,\ldots,k\) is obtained via the Lexical Procedure that can be lifted to a covering 1-factorization of \(M_k\) and subsequently collapsed onto a folding 1-factorization of \(R_k\). This insures the notation \(\delta(v)\) for each \(v\in V(R_k)\) so that there is a unique \(k\)-germ \(\alpha=\alpha(v)\) with \(\langle F(\alpha)\rangle=\delta(v)\).
Proof. As pointed out in (II) above, each SREP in \(M_k/\pi\) has its edges with a common color in \([k+1]\). Thus, the \([k+1]\)-coloring of \(M_k/\pi\) induces a well-defined \([k+1]\)-coloring of \(R_k\). This yields the claimed collapsing to a folding 1-factorization of \(R_k\). The lifting to a covering 1-factorization in \(M_k\) is immediate. The arguments above determine that the collapsing 1-factorization in \(R_k\) induces the claimed \(k\)-germs \(\alpha(v)\).
9. Union of lexical 1-factors of colors 0 and 1
Given a \(k\)-germ \(\alpha\), let \((\alpha)\) represent the dihedral class \(\delta(v)=\langle F(\alpha)\rangle\) with \(v\in L_k/\pi\). Let \(W_{01}^k\) be the 2-factor given by the union of the 1-factors of colors 0 and 1 in \(M_k\) (namely those formed by lifting the edges \(\alpha\alpha^0\) and \(\alpha\alpha^1\) of \(R_k\) in the notation of \ Section 12, instead of those of colors \(k\) and \(k-1\), as in [7]). The cycles of \(W_{01}^k\) are grown in this section from specific paths, as suggested in Figure 3 for \(k=2,3,4\) (say: cycle \(C_0\) that starts with vertically expressed path \(X(0)\), for \(k=2\); cycles \(C_0,C_1\) that start with vertically expressed paths \(X(0),X(1)\), for \(k=3\); and cycles \(C_0,C_1,C_2\) that start with vertically expressed paths \(X(0),X(1),X(2)\), for \(k=4\)). Here, vertices \(v\in L_k\) (resp. \(v\in L_{k+1}\)) will be represented with:- (a) 0- (resp. 1-) entries replaced by their respective colors \(0,1,\ldots,k\) (resp. asterisks);
- (b) 1- (resp. 0-) entries replaced by asterisks (resp. their respective colors \(0,1,\ldots,k\));
- (c) delimiting chevron symbols "\(>\)" or ``\(\rangle\)'' (resp. "\(< \)" or ``\(\langle\)''), instead of parentheses or brackets, indicating the reading direction of ``forward'' (resp. ``backward'') \(n\)-tuples.
Figure 3. Cycles of \(W_{01}^k\) in \(M_k\), (\(k=2,3,4\))
Observation 1. The initial entries of the vertices in each \(C_i\) are presented downward, first in the 0-column of \(X(i)\), then in the \((2k-j)\)-column of \(X(i)\), (\(j\in[2k]\), only up to \(|C_i|\).
In Figure 3, initial entries are red if they are in \(\{0,1\}\) and each cycle \(C_i\) is encoded on its top right by a vertical sequence of expressions \((0\cdots 1)(1\cdots 0)\) that allows to get the sequence of initial entries of the succeeding vertices of \(C_i\) by interspersing asterisks between each 2 terms inside parentheses (), then removing those ().An ordered tree \(T=T_v\) (Remark 1) for each \(v\) in the exemplified \(C_i(=C\) in Proposition 2(v) [7]) is shown at the lower right of its case in Figure 3. Each of these \(T_v\) for a specific \(C_i\) corresponds to the \(k\)-germ \(\alpha_v\) (so we write \(F(\alpha_v)=F(T_{\alpha_v})\)) and is headed in the figure by its (underlined decimal) natural order. In the figure, vertices of each \(T_v\) are denoted \(i\), instead of \(v_i\) (\(i\in[k+1]\)). The trees corresponding to the \(k\)-germs in each case are obtained by applying root rotation [7], consisting in replacing the tree root by its leftmost child and redrawing the ordered tree accordingly.
A plane tree is an equivalence relation of ordered trees under root rotations. In the notation of Section 12, applying one root rotation has the same effect as traversing first an edge \(\alpha\alpha_0\) in \(C_i\) and then edge \(\beta\beta_1\), also in \(C_i\), where \(\beta=\alpha_0\). In each case, a yellow box shows a subpath of \(X(i)\) with \(\frac{1}{n}|V(C_i)|\) vertices of \(C_i\) that takes into account the rotation symmetry of the associated plane tree \({\mathcal T}_i\).
In Figure 3 for \(k=4\), successive application of root rotations on the second cycle, \(C_1\), produces the cycle \((\underline{9},\underline{2},\underline{4},\underline{11},\underline{5},\underline{6},\underline{12},\underline{7})\), the square graph of \(C_1\), that starts downward from the second row or upward from the third row, thus covering respectively the vertices of \(L_4\) or \(L_5\) in the class.
Let \(D_i\) (\(i\ge 0\)) be the set of substrings of length \(2i\) in an \(F(\alpha)\) with exactly \(i\) color-entries such that in every prefix (i.e. initial substring), the number of asterisk-entries is at least as large as the number of color-entries. The elements of \(D=\cup_{i\ge 0}D_i\) are known as Dyck words. Each \(F(\alpha)\) is of the form \(0v1u*\), where \(u\) and \(v\) are Dyck words and 0 and 1 are colors in \([k+1]\) [7]. The ``forward'' \(n\)-tuple \(F(\alpha)\) in \((\underline{9},\underline{2},\underline{4},\underline{11},\underline{5},\underline{6},\underline{12},\underline{7})\) can be written with parentheses enclosing such Dyck words \(v\) and \(u\), namely \(0()1(34**2*)*\), for \(\underline{2}\); \(0(3*24**)1()*\), for \(\underline{9}\); \(0()1(3*24**)*\), for \(\underline{7}\); \(0(3*2*)1(4*)*\), for \(\underline{12}\); \(0(24*3**)1()*\), for \(\underline{6}\); \(0()1(24*3**)*\), for \(\underline{5}\); \(0(2*)1(4*3*)*\), for \(\underline{11}\); and \(0(34**2*)1()*\), for \(\underline{4}\). Similar treatment holds for ``backward'' \(n\)-tuples.
As in Figure 3, each pair \((0\cdots 1)(1\cdots 0)\) represents 2 paths in the corresponding cycle, of lengths \(2|(0\cdots 1)|-1\) and \(2|(1\cdots 0)|\),\ adding up to \(4k+2\). If these 2 paths are of the form \(0v1u*\) and \(0v'1u'*\) (this one read in reverse), then \(|u|+2=|(0\cdots 1)|\) and \(|u'|+2=|(1\cdots 0)|\). Reading these paths starts at a 0-entry and ends at a 1-entry. In reality, the collections of paths obtained from the 1-factors here have the leftmost entry of the \(n\)-tuples representing their vertices constantly equal to \(1\in\mathbb{Z}_2\) before taking into consideration (items (a) and (b) above, but with the reading orientations given in item (c).
The 1-factor of color 0 makes the endvertices of each of its edges to have their representative plane trees obtained from each other by horizontal reflection \(\Phi=F\alpha^0F^{-1}\). For example, Figure 3 shows that for \(k=2\): both \(\underline{0},\underline{1}\) in \(X(0)\) are fixed via \(\Phi\); for \(k=3\): \(\underline{0}\) in \(X(0)\) is fixed via \(\Phi\) and \(\underline{1},\underline{3}\) in \(X(0)\) correspond to each other via \(\Phi\); and \(\underline{2},\underline{4}\) in \(X(1)\) are fixed via \(\Phi\); for \(k=4\): \(\underline{0},\underline{8}\) in \(X(0)\) are fixed via \(\Phi\) and \(\underline{1},\underline{3}\) in \(X(0)\) correspond to each other via \(\Phi\); \(\underline{5},\underline{9}\) in \(X(1)\) are fixed via \(\Phi\) and the pairs \((\underline{5},\underline{9})\), \((\underline{2},\underline{7})\), \((\underline{4},\underline{12})\) and \((\underline{6},\underline{11})\) in \(X(1)\) are pairs of correspondent plane trees via \(\Phi\); and \(\underline{10},\underline{13}\) in \(X(2)\) are fixed via \(\Phi\). This horizontal reflection symmetry arises from Theorem 3. It accounts for each pair of contiguous rows in any \(X(i)\) corresponding to a 0-colored edge.
For \(k=5\), this symmetry via \(\Phi\) occurs in all cycles \(C_i\) (\(i\in[6]\)). But we also have \(F(\underline{22})=\rangle 024**135***\rangle\), where \(\underline{22}=(1111)\) in \(C_0\) and \(F(\underline{39})=\rangle 03*2*15*4**\rangle\), where \(\underline{39}=(1232)\) in \(C_3\), both having their 1-colored edges leading to reversed reading between \(L_5\) and \(L_6\), again by Theorem 3. Moreover, \(F((11\cdots 1))\) has a similar property only if \(k\) is odd; but if \(k\) is even, a 0-colored edge takes place, instead of the 1-colored edge for \(k\) odd. These cases reflect the following lemma (which can alternatively be implied from Theorem 10 (B)-(C)) via the correspondence \(i\leftrightarrow k-i\), (\(i\in[k+1]\)).
Observation 2.
- (A) Every \(0\)-colored edge is represented via \(\Phi=F\alpha^0F^{-1}\).
- (B) Every 1-colored edge is represented via the composition \(\Psi\) of \(\Phi\) (first) and root rotation (second).
Observation 3. For each integer \(k>1\), there is a natural bijection \(\Lambda\) from the \(k\)-edge plane trees onto the cycles of \(W_{01}^k\), as well as a partition \({\mathcal P}_k\) of the \(k\)-germs (or the ordered trees they represent via \(F\)), with each class of \({\mathcal P}_k\) in natural correspondence either to a \(k\)-edge plane tree or to a pair of enantiomorphic \(k\)-edge plane trees disconnecting in \(W_{01}^k\) the forward (in \(L_k\)) and reversed (in \(L_{k+1}\)) readings of each vertex \(v\) of their associated cycles via \(\Lambda\).
10. Reinterpretation of the middle-levels theorem
For each cycle \(C_i\) of \(W_{01}^k\), the ordered trees of its plane tree \({\mathcal T}_i\) with leftmost subpath of length 1 from \(v_0\) to a vertex \(v_h\) determine 6-cycles touching \(C_i\) in 2 nonadjacent edges as follows:Let \(t_i< k\) be the number of degree 1 vertices of \({\mathcal T}_i\). Let \(\tau_i\) be the number of rotation symmetries of \({\mathcal T}_i\). Then, there are \(\frac{t_i}{\tau_i}\) classes mod \(n\) of pairs of vertices \(u,v\) at distance 5 in \(C_i\) with \(u\in L_{k+1}\) ahead of \(v\in L_k\) in \(X(i)\) and associated color \(h\in\{2,\ldots,k\}\) such that:
- (i) \(u\) and \(v\) are adjacent via \(h\);
- (ii) \(u\) (resp. \(v\)) has cyclic backward (resp. forward) reading \(\langle\cdot\cdots * h 0 * \cdots\langle\) (resp. \(\rangle\cdots * 0 h *\cdots\cdot\rangle\));
- (iii) the column in which the occurrences of \(h\) in (ii) happen at distance 5 looks between \(u\) and \(v\) (both included) as the transpose of \((h,*,0,0,*,h)\). Recall there are \(n\) such columns.
The 6-cycle \(U_i^j=(uu'u''v''v'v)\) has as symmetric difference \(U_i^j\Delta(C_i\cup C_j)\) a cycle in \(M_k\) whose vertex set is \(V(C_i\cup C_j)\). With \(u',u'',v'',v',v,u,u'\) shown vertically, Figure 4 illustrates \(U_i^j\), twice each for \(k=3,4\).
That symmetric difference replaces respectively the edges \(u''v''\), \(v'v\), \(uu'\) in \(C_i\cup C_j\) by \(u'u''\), \(v''v''\), \(vu\). In the figure, vertically contiguous positions holding a common number \(g\) (meaning adjacency via color \(g\)) are presented in red if \(g\in\{0,1\}\), e.g. \(u''v''\) with \(g=1\), in column say \(r_1\) exactly at the position where \(u\) and \(v\) differ, (however having common color \(h\) as in (i) above) and in orange, otherwise. The column \(r_2\) (resp \(r_3\)) in each instance of Figure 3 containing color 1 in \(u'\) (resp. 0 in \(v'\)) and a color \(c\in\{2,\ldots,k\}\) in \(v'\) (resp. color \(d\in\{2,\ldots,k\}\) in \(u'\)) starts with \(1,*,c,c\), (resp. \(d,d,*,0\)), where \(c,d\in\{2,\ldots,k\}\). Then, \(r_1,r_2,r_3\) are the only columns having changes in the binary version of \(U_i^j\). All other columns have their first 4 entries alternating asterisks and colors. In the first disposition in item (ii) above, we have that: {\bf(ii')} \(u''\) (resp. \(v''\)) has cyclic backward (resp. forward) reading \(\langle\cdot\cdots d 1 0 * \cdots\langle\) (resp. \(\rangle\cdot\cdots * 1 * 0\cdots\rangle\)).
In the previous paragraph, ``ahead'' can be replaced by ``behind'', yielding additional 6-cycles \(U_i^j\) by modifying adequately the accompanying text.
Figure 4. Examples of 6-cycles \(U_i^j\) for \(k=4,5\)
Theorem 8.[6, 7] Let \(0< k\in\mathbb{Z}\). A Hamilton cycle in \(M_k\) is obtained by means of the symmetric differences of \(W_{01}^k\) with the members of a set of pairwise edge-disjoint 6-cycles \(U_i^j\).
Proof. Clearly, the statement holds for \(k=1\). Assume \(k>1\).
Let \(\mathcal D\) be the digraph whose vertices are the cycles \(C_i\) of \(W_{01}^k\), with an arc from \(C_i\) to \(C_j\), for each 6-cycle \(U_i^j\), where \(C_i,C_j\in V(\mathcal D)\) with \(i\ne j\). Since \(M_k\) is connected, then \(\mathcal D\) is connected.
Moreover, the outdegree and indegree of every \(C_i\) in \(\mathcal D\) is \(2n\frac{t_i}{\tau_i}\) (see items (ii) and (ii') above), in proportion with the length of \(C_i\), a \(\frac{1}{n}\)-th of which is illustrated in each yellow box of Figure 3.
Consider a spanning tree \({\mathcal D}'\) of \(\mathcal D\).
Since all vertices of \(\mathcal D\) have outdegree \(>0\), there is a \({\mathcal D}'\) in which the outdegree of each vertex is 1. This way, we avoid any pair of 6-cycles \(U_i^j\) with common \(C_i\) in which the associated distance-6 subpaths from \(u'\) to \(v\) in \(C_i\) do not have edges in common.
For each \(a\in A({\mathcal D}')\), let \(\nabla(a)\) be its associated 6-cycle \(U_i^j\). Then, \(\{\nabla(a);a\in A({\mathcal D}')\}\) can be selected as a collection of edge-disjoint 6-cycles. By performing all symmetric differences \(\nabla(a)\Delta(C_i\cup C_j)\) corresponding to these 6-cycles, a Hamilton cycle is obtained.
11. Alternate viewpoint on ordered trees
To have the viewpoint of [7], replace \(v_0\) by \(v_k\) as root of the ordered trees. We start with examples. Figure 5 shows on its left-hand side the 14 ordered trees for \(k=4\) encoded at the bottom of Table 1. Each such tree \(T=T(\alpha)\) is headed on top by its \(k\)-germ \(\alpha\), in which the entry \(i\) producing \(T\) via Castling is in red. Such \(T\) has its vertices denoted on their left and its edges denoted on their right, with their notation \(v_i\) and \(e_j\) given in Section 9. Castling here is indicated in any particular tree \(T=T(\alpha)\ne T(00\cdots 0)\) by distinguishing in red the largest subtree common with that of the parent tree of \(T\) (as in Theorem 1) whose Castling reattachment produces \(T\). This subtree corresponds with substring \(X\) in Theorem 2. In each case of such parent tree, the vertex in which the corresponding tree-surgery transformation leads to such a child tree \(T\) is additionally labeled (on its right) with the expression of its \(k\)-germ, in which the entry to be modified in the case is set in red color.On the other hand, the 14 trees in the right-hand side of Figure 5 have their labels set by making the root to be \(v_k\) (instead of \(v_0\)), then going downward to \(v_0\) (instead of \(v_k\)) while gradually increasing (instead of decreasing) a unit in the subindex \(j\) of the denomination \(v_j\), sibling by sibling from left to right at each level. The associated \(k\)-germ headers on this right-hand side of the figure correspond to the new root viewpoint. This determines a bijection \(\Theta\) established by correspondence between the old and the new header \(k\)-germs. In our example, it yields an involution formed by the pairs \((001,100)\), \((011,110)\), \((120,012)\) and \((112,121)\), with fixed 000, 010, 101, 111, 122 and 123.
Figure 5. Generation of ordered trees for \(k=4\)
This atom-parenthesizing procedure works for every \(k\)-germ \(\alpha\) and determines a corresponding base string \(\gamma\), like the \(\gamma'\) in our example.
Theorem 9. Given a \(k\)-germ \(\alpha=a_{k-1}a_{k-2}\cdots a_2a_1\), let \(a_i\) be the leftmost occurrence of its largest integer value. Then, \(\alpha\) is obtained from a base string \(\gamma=1\cdots a_i\) by inserting in \(\gamma\) all atoms of \(\alpha\setminus \gamma\) in their left-to-right order. Moreover, \(F^{-1}\Theta F(\alpha)\) is obtained by reversing the insertion of those atoms in \(\gamma\), in right-to-left fashion. For both insertions, \(\gamma\) is partitioned into subsequent atoms distributed in \(\alpha\) and \(F^{-1}\Theta F(\alpha)\) as further to the right as possible.
Proof. \(F^{-1}\Theta F(\alpha)\) is obtained by reversing the position of the parenthesized atoms, inserting them between the substrings of a partition of \(\gamma\) as the one above but for this reversing situation. In the above example of \(\alpha'\), it is \(F^{-1}\Theta F(\alpha')=(1)(12)(0)(1)12(234)34(23)(2)(0)\).
12. Germ structure of 1-factorizations
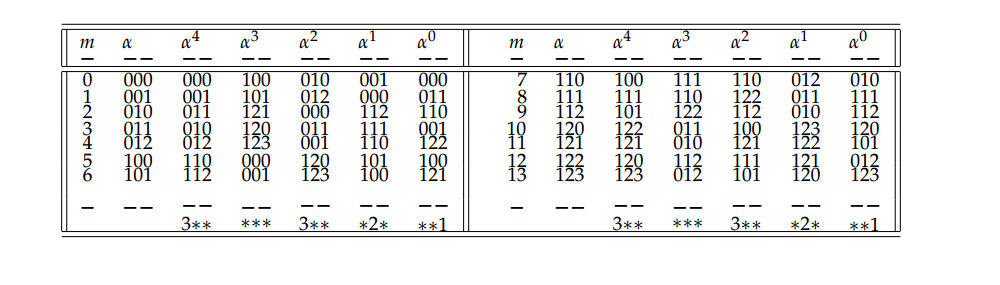
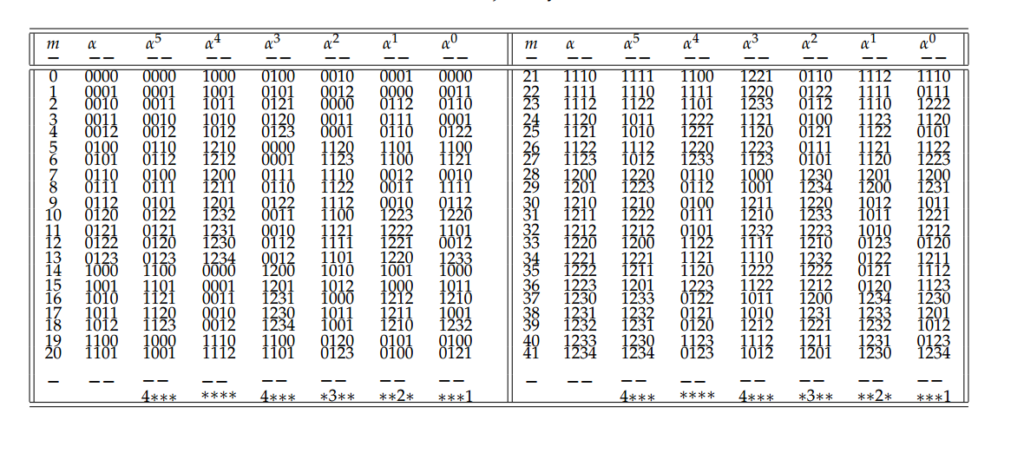
Table 4. Presentations \(\delta(v)=\{v,\aleph_\pi(v)\}\in R_k\), for \(k=2,3\), (\(v\in L_k/\pi\)).
To start with, examples of such presentation are shown in Table 4 for \(k=2\) and \(3\), where \(m\), \(\alpha=\alpha(m)\) and \(F(\alpha)\) are shown in the first 3 columns, for \(0\le m< C_k\). The neighbors of \(F(\alpha)\) are presented in the central columns of the table as \(F^k(\alpha)\), \(F^{k-1}(\alpha)\), \(\ldots\), \(F^0(\alpha)\) respectively for the edge colors \(k,k-1,\ldots,0\), with notation given via the effect of function \(\aleph\). The last columns yield the \(k\)-germs \(\alpha^k\), \(\alpha^{k-1}\), \(\ldots\), \(\alpha^0\) associated via \(F^{-1}\) respectively to the listed neighbors \(F^k(\alpha)\), \(F^{k-1}(\alpha)\) , \(\ldots\), \(F^0(\alpha)\) of \(F(\alpha)\) in \(R_k\).
Table 5. Colored Adjacency Table CAT(4).
Table 6. Colored Adjacency Table CAT(5).
Theorem 10. Let: \(k>1\), \(j(\alpha^k)=k-1\) and \(j(\alpha^{i-1})=i\), (\(i=k-1,\ldots,1\)). Then:
- (A) each column \(\alpha^{i-1}\) in CAT\((k)\), for \(i\in[k]\cup\{k+1\}\), preserves the respective \(j(\alpha^{i-1})\)-th entry of \(\alpha\);
- (B) the columns \(\alpha^k\) of all CAT\((k)\)'s for \(k>1\) coincide into an RGS sequence and thus into an integer sequence \({\mathcal S}_0\), the first \(C_k\) terms of which form an idempotent permutation for each \(k\);
- (C) the integer sequence \({\mathcal S}_1\) given by concatenating the \(m\)-indexed intervals \([0,2),[2,5), \ldots,\) \([C_{k-1},C_k)\), etc. in column \(\alpha^{k-1}\) of the corresponding tables CAT\((2)\), CAT\((3),\ldots\), CAT\((k)\), etc. allows to encode all columns \(\alpha^{k-1}\)'s;
- (D) for each \(k>1\), there is an idempotent permutation given in the \(m\)-indexed interval \([0,C_k)\) of the column \(\alpha^{k-1}\) of CAT\((k)\); such permutation equals the one given in the interval \([0,C_k)\) of the column \(\alpha^{k-2}\) of CAT\((k+1)\).
Proof. (A)holds as a continuation of the observation made above with respect to the last aggregated row in Figure 5. Let \(\alpha\) be a \(k\)-germ. Then \(\alpha\) shares with \(\alpha^k\) (e.g. the leftmost column \(\alpha^i\) in Tables 4, 5 and 6, for \(0\le i\le k\)) all the entries to the left of the leftmost entry 1, which yields (B). Note that if \(k=3\) then \(m=2,3,4\) yield for \(\alpha^{k-1}\) the idempotent permutation \((2,0)(4,1)\), illustrating (C). (D) can be proved similarly.
The sequences in Theorem 10 (B)-(C) start as follows, with intervals ended in ``;'': $$\begin{array}{rrrrrrrrrrrrrrrrrr} ^{\{0\}\cup\mathbb{Z}^+=}&^{0,}&^{1;}&^{2,}&^{3,}&^{4;}&^{5,}&^{6,}&^{7,}&^{8,}&^{9,}&^{10,}&^{11,}&^{12,}&^{13;}&^{14}&^{15,}&^{16,\ldots}\\\hline ^{(B)=}_{(C)=}&^{0,}_{1,}&^{1;}_{0;}&^{3,}_{0,}&^{2,}_{3,}&^{4;}_{1;}&^{7,}_{0,}&^{9,}_{1,}&^{5,}_{8,}&^{8,}_{7,}&^{\hspace{1mm}6,}_{12,}&^{12,}_{\hspace{1mm}3,}&^{11,}_{\hspace{1mm}2,}&^{10,}_{\hspace{1mm}9,}&^{13;}_{\hspace{1mm}4;}&^{19,}_{\hspace{1mm}0,}&^{20,}_{\hspace{1mm}1,}&^{25,\ldots}_{\hspace{1mm}3,\ldots}\\ \end{array}$$Remark 2. With the notation of Section 11 and Theorem 9, for each of the involutions \(\alpha^i\) (\(0< i< k \)), it holds that \(\alpha^i\Theta=\Theta\alpha^{k-i}\). This implies that
- (A) every \(k\)-colored edge represents an adjacency via \(\Phi'=F\alpha_kF^{-1}\) and
- (B) every \((k-1)\)-colored edge represents an adjacency via \(\Psi'=F\Psi F^{-1}\).
- (a) the reverse string off \(\alpha'\) be \(\psi(\alpha')=a_{k-i}\cdots a_{k-j}\);
- (b) the ascent of \(\alpha'\) be
- (i) its maximal initial ascending substring, if \(a_{k-j}=0\), and
- (ii) its maximal initial non-descending substring with at most 2 equal nonzero terms, if \(a_{k-j}>0\).
Remark 3. Assume \(p=k\). If \(a_{k-1}=1\), take \(0|\alpha\) instead of \(\alpha=a_{k-1}\cdots a_1\), with \(k-1\) instead of \(k\), removing afterwards from the resulting \(\beta\) the added leftmost 0. Now, let \(\alpha_1=a_{k-1}\cdots a_{k-i_1}\) be the ascent of \(\alpha\). Let \(B_1=i_1-1\), where \(i_1=||\alpha_1||\) is the length of \(\alpha_1\). It can be seen that \(\beta\) has ascent \(\beta_1=b_{k-1}\cdots b_{k-i_1}\) with \(\alpha_1+\psi(\beta_1)=B_1\cdots B_1\). If \(\alpha\ne\alpha_1\), let \(\alpha_2\) be the ascent of \(\alpha\setminus\alpha_1\). Then there is a \(||\alpha_2||\)-germ \(\beta_2\) with \(\alpha_2+\psi(\beta_2)=B_2\cdots B_2\) and \(B_2=||\alpha_1||+||\alpha_2||-2\). Inductively when feasible for \(j>2\), let \(\alpha_j\) be the ascent of \(\alpha\setminus(\alpha_1|\alpha_2|\cdots|\alpha_{j-1})\). Then there is a \(||\alpha_j||\)-germ \(\beta_j\) with \(\alpha_j+\psi(\beta_j)=B_j\cdots B_j\) and \(B_j=||\alpha_{j-1}||+||\alpha_j||-2\). This way, \(\beta=\beta_1|\beta_2|\cdots|\beta_j|\cdots\).
Remark 4. Assume \(k>p>0\). By Theorem 10 (A), if \(p< k -1\), then \(b_{p+1}=a_{p+1}\); in this case, let \(\alpha'=\alpha\setminus\{a_{k-1}\cdots a_q\}\) with \(q=p+1\). If \(p=k-1\), let \(q=k\) and let \(\alpha'=\alpha\).
In both cases (either \(p< k-1\) or \(p=k-1\)) let \(\alpha'_1=a_{q-1}\cdots a_{k-i_1}\) be the ascent of \(\alpha'\). It can be seen that \(\beta'=\beta\setminus\{b_{k-1}\cdots b_q\}\) has ascent \(\beta'_1=b_{k-1}\cdots b_{k-i_1}\) where \(\alpha'_1+\psi(\beta'_1)=B'_1\cdots B'_1\) with \(B'_1=i_1+a_q\).
If \(\alpha'\ne\alpha'_1\) then let \(\alpha'_2\) be the ascent of \(\alpha'\setminus\alpha'_1\). Then
there is a \(||\alpha'_2||\)-germ \(\beta'_2\) where \(\alpha'_2+\psi(\beta'_2)=B'_2\cdots B'_2\) with \(B'_2=||\alpha'_1||+||\alpha'_2||-2\). Inductively when feasible for \(j>2\), let \(\alpha_j\) be the ascent of \(\alpha'\setminus(\alpha'_1|\alpha'_2|\cdots|\alpha'_{j-1})\). Then there is a \(||\alpha'_j||\)-germ \(\beta'_j\) where \(\alpha'_j+\psi(\beta'_j)=B'_j\cdots B'_j\) with \(B'_j=||\alpha'_{j-1}||+||\alpha'_j||-2\). This way, \(\beta'=\beta'_1|\beta'_2|\cdots|\beta'_j|\cdots\).
We process the left-hand side from position \(q\). If \(p>1\), we set \(a_{a_q+2}\cdots a_q +\psi(b_{b_q+2}\cdots b_q)\) to equal a constant string \(B\cdots B\), where \(a_{a_q+2}\cdots a_q\) is an ascent and \(a_{a_q+2}=b_{b_q+2}\).
Expressing all those numbers \(a_i,b_i\) as \(a_i^0,b_i^0\), respectively, in order to keep an inductive approach, let \(a^1_q=a_{a_q+2}\). While feasible, let \(a^1_{q+1}=a_{a_q+1}\), \(a^1_{q+2}=a_{a_q}\) and so on. In this case, let \(b^1_q=b_{b_q+2}\), \(b^1_{q+1}=b_{b_q+1}\), \(b^1_{q+2}=b_{b_q}\) and so on. Now, \(a^1_{a^1_q+2}\cdots a^1_q+\psi(b^1_{b^1_q+2}\cdots b^1_q)\) equals a constant string, where \(a^1_{a^1_q+2}\cdots a^1_q\) is an ascent and \(a^1_{a^1_q+2}=b^1_{b^1_q+2}\). The continuation of this procedure produces a subsequent string \(a^2_q\) and so on, until what remains to reach the leftmost entry of \(\alpha\) is smaller than the needed space for the procedure itself to continue, in which case, a remaining initial ascent is shared by both \(\alpha\) and \(\beta\). This allows to form the left-hand side of \(\alpha^p=\beta\) by concatenation.
Conflict of Interests
The author declares no conflict of interest.References
- Kierstead, H. A., & Trotter, W. T. (1988). Explicit matchings in the middle levels of the Boolean lattice. Order, 5, 163--171.[Google Scholor]
- Shields, I., & Savage, C. (1999). A Hamilton path heuristic with applications to the middle 2 levels problem. Congr. Num., 140, 161--178.[Google Scholor]
- Sloane, N. J. A., The On-Line Encyclopedia of Integer Sequences. http://oeis.org/.[Google Scholor]
- Arndt, J. (2010). Matters Computational: ideas, algorithms, source code. Springer Science & Business Media.[Google Scholor]
- Stanley, R. P. (1999). Enumerative Combinatorics, vol. 2. 1999. Search Results Web results Cambridge Studies in Advanced Mathematics.[Google Scholor]
- Gregor, P. , & Mütze, T., & Nummenpalo, J. (2018). A short proof of the middle levels theorem. Discrete Analysis, 8, 12pp.[Google Scholor]
- Mütze, T., (2016). Proof of the middle levels conjecture. Proceedings of the London Mathematical Society -, 112, 677--713.[Google Scholor]