Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2020.0044
\(C_6\)-decompositions of the tensor product of complete graphs
Department of Mathematics, Federal University of Agriculture, Makurdi, Nigeria.; (A.D.A)
Department of Mathematics, Air Force Institute of Technology, Kaduna, Nigeria.; (O.O)
\(^{1}\)Corresponding Author: opeyemioluwaoyewumi@gmail.com; Tel.: +2348154792760
Abstract
Keywords:
1. Introduction
Let \(C_m\), \(K_m\) and \(K_m -I\) denote cycle of length \(m\), complete graph on \(m\) vertices and complete graph on \(m\) vertices minus a \(1\)-factor respectively. By an \(m\)-cycle we mean a cycle of length \(m\). All graphs considered in this paper are simple and finite. A graph is said to be decomposed into subgraphs \(H_1\) and \(H_2\) which is denoted by \(G= H_1 \oplus H_2\), if \(G\) is the edge disjoint union of \(H_1\) and \(H_2\). If \(G= H_1 \oplus H_2 \oplus \cdots \oplus H_k\), where \(H_1\), \(H_2\), ..., \(H_k\) are all isomorphic to \(H\), then \(G\) is said to be \(H\)-decomposable. Furthermore, if \(H\) is a cycle of length \(m\) then we say that \(G\) is \(C_m\)-decomposable and this can be written as \(C_m|G\). A \(k\)-factor of \(G\) is a \(k\)-regular spanning subgraph. A \(k\)-factorization of a graph \(G\) is a partition of the edge set of \(G\) into \(k\)-factors. A \(C_k\)-factor of a graph is a \(2\)-factor in which each component is a cycle of length \(k\). A resolvable \(k\)-cycle decomposition (for short \(k\)-RCD) of \(G\) denoted by \(C_k ||G\), is a \(2\)-factorization of \(G\) in which each \(2\)-factor is a \(C_k\)-factor.
For two graphs \(G\) and \(H\) their tensor product \(G \times H\) has vertex set \(V(G) \times V(H)\) in which two vertices \((g_1,h_1)\) and \((g_2,h_2)\) are adjacent whenever \(g_1g_2 \in E(G)\) and \(h_1h_2 \in E(H)\). From this, note that the tensor product of graphs is distributive over edge disjoint union of graphs, that is if \(G= H_1 \oplus H_2 \oplus \cdots \oplus H_k\), then \(G \times H = (H_1 \times H)\oplus (H_2 \times H) \oplus \cdots \oplus(H_k \times H)\). Now, for \(h \in V(H)\), \(V(G) \times h = \{(v,h)|v \in V(G)\}\) is called a column of vertices of \(G \times H\) corresponding to \(h\). Further, for \(y \in V(G)\), \(y \times V(H) = \{(y,v)|v \in V(H)\}\) is called a layer of vertices of \(G \times H\) corresponding to \(y\).
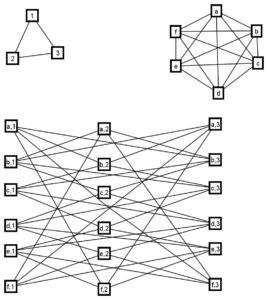
Figure 1. The tensor product \(C_3 \times K_6\). \(C_3\) and \(K_6\) are shown at the top of the product respectively.
In [1], Oyewumi et al., obtained an interesting result on the decompositions of certain graphs. The problem of finding \(C_k\)-decomposition of \(K_{2n+1}\) or \(K_{2n}-I\) where \(I\) is a \(1\)-factor of \(K_{2n}\), is completely settled by Alspach, Gavlas and Sajna in two different papers (see [2,3]). A generalization to the above complete graph decomposition problem is to find a \(C_k\)-decomposition of \(K_m \ast \overline K_n\), which is the complete \(m\)-partite graph in which each partite set has \(n\) vertices. The study of cycle decompositions of \(K_m \ast \overline K_n\) was initiated by Hoffman et al., [4]. In the case when \(p\) is a prime, the necessary and sufficient conditions for the existence of \(C_p\)-decomposition of \(K_m \ast \overline K_n\), \(p\geq 5\) is obtained by Manikandan and Paulraja in [5,6,7]. Billington [8] studied the decomposition of complete tripartite graphs into cycles of length 3 and 4. Furthermore, Cavenagh and Billington [9] studied \(4\)-cycle, \(6\)-cycle and \(8\)-cycle decomposition of complete multipartite graphs.
Billington et al., [10] solved the problem of decomposing \((K_m \ast \overline K_n)\) into \(5\)-cycles. Similarly, when \(p \geq 3\) is a prime, the necessary and sufficient conditions for the existence of \(C_{2p}\)-decomposition of \(K_m \ast \overline K_n\) was obtained by Smith (see [11]). For a prime \(p \geq 3\), it was proved in [12] that \(C_{3p}\)-decomposition of \(K_m \ast \overline K_n\) exists if the obvious necessary conditions are satisfied. As the graph \(K_m \times K_n \cong K_m \ast \overline K_n - E(nK_m)\) is a proper regular spanning subgraph of \(K_m \ast \overline K_n\). It is natural to think about the cycle decomposition of \(K_m \times K_n\).
The results in [5,6,7] also give necessary and sufficient conditions for the existence of a \(p\)-cycle decomposition, (where \(p \geq 5\) is a prime number) of the graph \(K_m \times K_n\). In [13] it was shown that the tensor product of two regular complete multipartite graph is Hamilton cycle decomposable. Muthusamy and Paulraja in [14] proved the existence of \(C_{kn}\)-factorization of the graph \(C_k \times K_{mn}\), where \(mn \neq 2 (\textrm{mod}\ 4)\) and \(k\) is odd. While Paulraja and Kumar [15] showed that the necessary conditions for the existence of a resolvable \(k\)-cycle decomposition of tensor product of complete graphs are sufficient when \(k\) is even. Oyewumi and Akwu [16] proved that \(C_4\) decomposes the product \(K_m \times K_n\), if and only if either (1) \(n \equiv 0 \ (\textrm{mod}\ 4)\) and \(m\) is odd, (2) \(m \equiv 0 \ (\textrm{mod}\ 4)\) and \(n\) is odd or (3) \(m \ or \ n \equiv 1 \ (\textrm{mod}\ 4)\).
As a companion to the work in [16], i.e., to consider the decomposition of the tensor product of complete graphs into cycles of even length. This paper proves that the obvious necessary conditions for \(K_m \times K_n\), \(2 \leq m,n\), to have a \(C_6\)-decomposition are also sufficient. Among other results, here we prove the following main results.
It is not surprising that the conditions in Theorem 1 are "symmetric" with respect to \(m\) and \(n\) since \(K_m \times K_n \cong K_n \times K_m\).
Theorem 1. Let \(2 \leq m,n, \) then \(C_6| K_m \times K_n\) if and only if \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\) or \(n \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\).
Theorem 2. Let \(m\) be an even integer and \(m \geq 6\), then \(C_6| K_m - I \times K_n\) if and only if \(m \equiv 0 \ \text{or} \ 2\ (\textrm{mod}\ 6)\).
2. \(C_6\) decomposition of \(C_3 \times K_n\)
Theorem 3. Let \(n \in N\), then \(C_6|C_3 \times K_n\).
Proof. Following from the definition of tensor product of graphs, let \(U^1= \{u_1,v_1,w_1\}\), \(U^2= \{u_2,v_2,w_2\} \),\(...\), \(U^n=\{u_n,v_n,w_n\}\) form the partite set of vertices in \(C_3 \times K_n\). Also, \(U^i\) and \(U^j\) has an edge in \(C_3 \times K_n\) for \(1\leq i,j\leq n\) and \(i\neq j\) if the subgraph induce \(K_{3,3}-I\), where \(I\) is a \(1\)-factor of \(K_{3,3}\). Now, each subgraph \(U^i \cup U^j\) is isomorphic to \(K_{3,3}-I\). But \(K_{3,3}-I\) is a cycle of length six. Hence the proof.
Example 1. The graph \(C_3 \times K_7\) can be decomposed into cycles of length \(6\).
Proof. Let the partite sets (layers) of the tripartite graph \(C_3 \times K_7\) be \(U=\{u_1, u_2, . . . , u_7\}\), \(V=\{v_1, v_2, . . . , v_7\}\) and \(W=\{w_1,w_2, . . . ,w_7\}\). We assume that the vertices of \(U,V\) and \(W\) having same subscripts are the corresponding vertices of the partite sets. A \(6\)-cycle decomposition of \(C_3 \times K_7\) is given below:
\(\{u_1,v_2,w_1,u_2,v_1,w_2\}\),\(\{u_1,v_3,w_1,u_3,v_1,w_3\}\),\(\{u_2,v_3,w_2,u_3,v_2,w_3\}\),
\(\{u_1,v_4,w_1,u_4,v_1,w_4\}\),\(\{u_2,v_4,w_2,u_4,v_2,w_4\}\),\(\{u_3,v_4,w_3,u_4,v_3,w_4\}\),
\(\{u_1,v_5,w_1,u_5,v_1,w_5\}\),\(\{u_2,v_5,w_2,u_5,v_2,w_5\}\),\(\{u_3,v_5,w_3,u_5,v_3,w_5\}\),
\(\{u_4,v_5,w_4,u_5,v_4,w_5\}\),\(\{u_1,v_6,w_1,u_6,v_1,w_6\}\),\(\{u_2,v_6,w_2,u_6,v_2,w_6\}\),
\(\{u_3,v_6,w_3,u_6,v_3,w_6\}\),\(\{u_4,v_6,w_4,u_6,v_4,w_6\}\),\(\{u_5,v_6,w_5,u_6,v_5,w_6\}\),
\(\{u_1,v_7,w_1,u_7,v_1,w_7\}\),\(\{u_2,v_7,w_2,u_7,v_2,w_7\}\),\(\{u_3,v_7,w_3,u_7,v_3,w_7\}\),
\(\{u_4,v_7,w_4,u_7,v_4,w_7\}\),\(\{u_5,v_7,w_5,u_7,v_5,w_7\}\),\(\{u_6,v_7,w_6,u_7,v_6,w_7\}\).
Theorem 4. [17] Let \(m\) be an odd integer and \(m \geq 3\). If \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\) then \(C_3|K_m\).
Theorem 5. [3] Let \(n\) be an even integer and \(m\) be an odd integer with \(3 \leq m \leq n\). The graph \(K_n- I\) can be decomposed into cycles of length \(m\) whenever \(m\) divides the number of edges in \(K_n - I\).
3. \(C_6\) decomposition of \(C_6 \times K_n\)
Theorem 6. [3] Let \(n\) be an odd integer and \(m\) be an even integer with \(3 \leq m \leq n\). The graph \(K_n\) can be decomposed into cycles of length \(m\) whenever \(m\) divides the number of edges in \(K_n\).
Lemma 1. \(C_6|C_6 \times K_2\).
Proof. Let the partite set of the bipartite graph \(C_6 \times K_2\) be \(\{u_1,u_2,...,u_6\}\), \(\{v_1,v_2,...,\) \(v_6\}\). We assume that the vertices having the same subscripts are the corresponding vertices of the partite sets. Now \(C_6 \times K_2\) can be decomposed into \(6\)-cycles which are \(\{u_1,v_2,u_3,v_4,u_5,v_6\}\) and \(\{v_1,u_2,v_3,u_4,v_5,u_6\}\).
Theorem 7. For all \(n\), \(C_6|C_6 \times K_n\).
Proof. Let the partite set of the \(6\)-partite graph \(C_6 \times K_n\) be \(U=\{u_1,u_2,...,u_n\}\), \(V=\{v_1,v_2,...,v_n\}\), \(W=\{w_1,w_2,...,w_n\}\), \(X=\{x_1,x_2,...,x_n\}\), \(Y=\{y_1,y_2,...,y_n\}\) and \(Z=\{z_1,z_2,...,z_n\}\), we assume that the vertices of \(U,V,W,X,Y\) and \(Z\) having the same subscripts are the corresponding vertices of the partite sets. Let \(U^1=\{u_1,v_1,w_1,x_1,y_1,z_1\}\), \(U^2=\{u_2,v_2,w_2,x_2,y_2,z_2\}\), ..., \(U^n=\{u_n,v_n,w_n,x_n,y_n,z_n\}\) be the sets of these vertices having the same subscripts. By the definition of the tensor product, each \(U^i\), \(1 \leq i \leq n\) is an independent set and the subgraph induced by each \(U^i \cup U^j\), \(1\leq i,j\leq n\) and \(i\neq j\) is isomorphic to \(C_6 \times K_2\). Now by Lemma 1 the graph \(C_6 \times K_2\) admits a \(6\)-cycle decomposition. This completes the proof.
4. \(C_6\) decomposition of \(K_m \times K_n\)[Proofs of main Theorems]
Proof of Theorem 1. Assume that \(C_6|K_m \times K_n\) for some \(m\) and \(n\) with \(2 \leq m,n\). Then every vertex of \(K_m \times K_n\) has even degree and \(6\) divides in the number of edges of \(K_m \times K_n\). These two conditions translate to \((m-1)(n-1)\) being even and \(6|m(m-1)n(n-1)\) respectively. Hence, by the first fact \(m\) or \(n\) has to be odd, i.e., has to be congruent to \(1 \ or \ 3 \ or \ 5\ (\textrm{mod}\ 6)\). The second fact can now be used to show that they cannot both be congruent to \(5\ (\textrm{mod}\ 6)\). It now follows that \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\) or \(n \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\).
Conversely, let \(m \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\). By Theorem 4, \(C_3|K_m\) and hence \(K_m \times K_n =((C_3 \times K_n)\oplus \cdots \oplus(C_3 \times K_n))\). Since \(C_6|C_3 \times K_n\) by Theorem 3.
Finally, if \(n \equiv 1 \ or \ 3\ (\textrm{mod}\ 6)\), the above argument can be repeated with the roles of \(m\) and \(n\) interchanged to show again that \(C_6|K_m \times K_n\). This completes the proof.Proof of Theorem 2. Assume that \(C_6|K_m-I \times K_n, m\geq 6\). Certainly, \(6|mn(m-2)(n-1)\). But we know that if \(6|m(m-2)\) then \(6|mn(m-2)(n-1)\). But \(m\) is even therefore \(m \equiv 0 \ or \ 2\ (\textrm{mod}\ 6)\).
Conversely, let \(m \equiv 0 \ or \ 2 \ (\textrm{mod}\ 6)\). Notice that for each \(m\), \(\frac{m(m-2)}{2}\) is a multiple of \(3\). Thus by Theorem 5 \(C_3|K_m -I\) and hence \(K_m - I \times K_n =((C_3 \times K_n)\oplus \cdots \oplus(C_3 \times K_n))\). From Theorem 3, \(C_6|C_3 \times K_n\). The proof is complete.
5. Conclusion
In view of the results obtained in this paper we draw our conclusion by the following corollary.Corollary 1. For any simple graph \(G\). If
- 1. \(C_3 |G\) then \(C_6 |G \times K_n\), whenever \(n \geq 2\).
- 2. \(C_6 |G\) then \(C_6 |G \times K_n\), whenever \(n \geq 2\).
Proof. We only need to show that \(C_3|G\). Applying Theorem 3 gives the result.
Acknowledgments
The authors would like to thank the referees for helpful suggestions which has improved the present form of this work.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflict of Interests
The authors declare no conflict of interest.References
- Oyewumi, O., Akwu, A. D. & Azer, T. I. (2018). Path decomposition number of certain graphs. Open Journal of Discrete Applied Mathematics, 1(1), 26-32. [Google Scholor]
- Alspach, B. & Gavlas, H. (2001). Cycle decompositions of \(K_n\) and \(K_n-I\). Journal of Combinatorial Theory, Series B, 81, 77-99. [Google Scholor]
- Sajna, M. (2002). Cycle decompositions III: complete graphs and fixed length cycles. Journal of Combinatorial Designs, 10, 27-78. [Google Scholor]
- Hoffman, D. G., Linder, C. C. & Rodger, C. A. (1989). On the construction of odd cycle systems. Journal of Graph Theory, 13, 417-426. [Google Scholor]
- Manikandan, R. S., & Paulraja, P. (2006). (2006). \(C_p\)-decompositions of some regular graphs. Discrete Mathematics, 306(4), 429-451. [Google Scholor]
- Manikandan, R.S. & Paulraja, P. (2007). \(C_5\)-decompositions of the tensor product of complete graphs. Australasian Journal of Combinatorics, 37, 285-293. [Google Scholor]
- Manikandan, R.S. & Paulraja, P. (2017). \(C_7\)-decompositions of the tensor product of complete graphs. Discussiones Mathematicae Graph Theory, 37(3), 523-535. [Google Scholor]
- Billington, E. J. (1999). Decomposing complete tripartite graphs into cycles of lengths 3 and 4. Discrete Mathematics, 197, 123-135. [Google Scholor]
- Cavenagh, N. J., & Billington, E. J. (2000). Decompositions of complete multipartite graphs into cycles of even length. Graphs and Combinatorics, 16(1), 49-65. [Google Scholor]
- Billington, E. J., Hoffman, D. G., & Maenhaut, B. H. (1999). Group divisible pentagon systems. Utilitas Mathematica, 55, 211-219.[Google Scholor]
- Smith, B. R. (2006). Decomposing complete equipartite graphs into cycles of lenght \(2p\). Journal of Combinatorial Designs, 16(3), 244-252. [Google Scholor]
- Smith, B. R. (2009). Complete equipartite \(3p\)-cycle systems. Australasian Journal of Combinatorics, 45, 125-138. [Google Scholor]
- Manikandan, R. S., & Paulraja, P. (2008). Hamilton cycle decompositions of the tensor product of complete multipartite graphs. Discrete mathematics, 308(16), 3586-3606. [Google Scholor]
- Muthusamy, A., & Paulraja, P. (1995). Factorizations of product graphs into cycles of uniform length. Graphs and Combinatorics, 11(1), 69-90. [Google Scholor]
- Paulraja, P., & Kumar, S. S. (2011). Resolvable even cycle decompositions of the tensor product of complete graphs. Discrete Mathematics, 311(16), 1841-1850. [Google Scholor]
- Oyewumi, O. & Akwu, A. D. (2020). \(C_4\) decomposition of the tensor product of complete graphs. Electronic Journal of Graph Theory and Applications, 8(1), 9-15. [Google Scholor]
- Lindner, C.C. & Rodger, C.A. (1997). Design Theory. CRC Press New York. [Google Scholor]