Numerical analysis of a quasistatic contact problem for piezoelectric materials

1. Introduction

The piezoelectric phenomenon represents the coupling between the mechanical and the electrical behavior of a class of materials, called piezoelectric materials. In the simplest of terms, when a piezoelectric material is squeezed, an electric charge collects on its surface; conversely, when a piezoelectric material is subjected to a voltage drop, it mechanically deforms. Piezoelectric materials present a great importance in the development hight technological applications such as actuators, sensors, engineering control equipments or smart materials and structures, because of the coupling effects between mechanical and electric fields. During the last years, there is a considerable mathematical interest in frictional contact problems involving piezoelectric materials, under the assumption that the foundation is electrically conductive (see, [1,2,3,4,5,6,7]). The results in [1,5,6] concern the variational formulation of the problems and their unique week solvability while the results in [2,3,4,7] concern mainly the numerical simulation of the problems.

In this work, we numerically analyse and simulate a model for the process of frictional contact between an electro-viscoelastic body and a conductive foundation. The contact is modeled by the normal compliance condition and the associated Coulomb’s law of dry friction. This paper continues [1,5], providing the numerical modelling of the problem supported by numerical simulations. In [1], we established the result of existence of solution without a smallness assumption given in [5], from now on, this will not represents a physical obstacle to study numerically a contact problems with a deformable and conductive foundation. The analysis and numerical approach of this system represent the main trait of novelty of the present paper. To this end, we introduce a fully discrete approximation scheme and derive error estimates. The frictional contact conditions are treated by using a numerical approach based on the combination of the penalized method and the augmented Lagrangian method (see [8,9] for details). We implement this scheme in a numerical code and present numerical simulations in the study of two-dimensional test problem.

The paper is organized as follows. In Section 2 we present a brief description of the mechanical model and its variational formulation. A fully discrete scheme is presented in Section 3, based on the finite element method to approximate the spatial variable and the Euler scheme to discretize the time derivatives. A main error estimates result is proved, Theorem 2, from which the linear convergence of the algorithm is deduced under suitable regularity conditions. The numerical algorithm used for solving the discrete problem is described in Section 4, where some numerical simulations are also presented in order to demonstrate the accuracy and the performance of the method. Finally, in Section 5 we present some conclusions and perspectives.

2. The model

We consider a body made of a piezoelectric material which occupies the domain \(\Omega \subset{\mathbb{R}}^d,\,\, d=2,3 \) with a smooth boundary \(\partial \Omega=\Gamma\) and a unit outward normal \(\boldsymbol{\nu}=(\nu_i)\). The body is acted upon by body forces of density \(\boldsymbol{f}_0\) and has volume electric charges of density \(q_0\). It is also constrained mechanically and electrically on the boundary. To describe these constraints we consider a partition of \(\Gamma\) into three open disjoint parts \(\Gamma_D\), \(\Gamma_N\) and \(\Gamma_C\), on the one hand, and a partition of \(\Gamma_D\cup\Gamma_N\) into two open parts \(\Gamma_a\) and \(\Gamma_b\) , on the other hand. We assume that \(meas\,\Gamma_1>0\) and \(meas\,\Gamma_a>0\). The body is clamped on \(\Gamma_D\) and therefore the displacement field vanishes there. Surface tractions of density \(\boldsymbol{f}_N\) act on \(\Gamma_N\). We also assume that the electrical potential vanishes on \(\Gamma_a\) and a surface electrical charge of density \(q_b\) is prescribed on \(\Gamma_b\) . In the reference configuration, the body is in contact over \(\Gamma_C\) with a deformable obstacle, the so called foundation. We assume that the foundation is electrically conductive and its potential is maintained at \(\varphi_f\). The contact is frictional and there may be electrical charges on the contact surface.

We denote by \(\mathbb{S}^d\) the space of second order symmetric tensors on \(\mathbb{R}^d\) or, equivalently, the space of symmetric matrices of order \(d\), and \(“\cdot”\) and \(\|\cdot\|\) represent the inner product and the Euclidean norm on \(\mathbb{R}^d\) and \(\mathbb{S}^d\), respectively, that is \(\boldsymbol{u}\cdot\boldsymbol{v} = u_i v_i,\, \|\boldsymbol{v}\|=(\boldsymbol{v}\cdot \boldsymbol{v})^{1/2}\mbox{ for } \boldsymbol{u}, \boldsymbol{v}\in \mathbb{R}^d,\mbox{ and } \boldsymbol{\sigma}\cdot\boldsymbol{\tau} = \sigma_{ij}\tau_{ij},\; \|\boldsymbol{\tau}\| = (\boldsymbol{\tau}\cdot\boldsymbol{\tau})^{1/2}\mbox{ for } \boldsymbol{\sigma},\boldsymbol{\tau}\in \mathbb{S}^d\). We also use the usual notation for the normal components and the tangential parts of vectors and tensors, respectively, by \(u_\nu = \boldsymbol{u}\cdot\boldsymbol{\nu},\; \boldsymbol{u}_\tau = \boldsymbol{u}- u_\nu\boldsymbol{\nu},\; \boldsymbol{\sigma}_\nu = \sigma_{ij}\nu_i\nu_j\), and \(\boldsymbol{\sigma}_\tau = \boldsymbol{\sigma}\boldsymbol{\nu}-\sigma_\nu\boldsymbol{\nu}\). Here and everywhere in this paper \(i, j, k, l\) run from 1 to \(d\), summation over repeated indices is implied and the index that follows a comma represents the partial derivative with respect to the corresponding component of the spatial variable, i.e. \(f_{,i}=\frac{\partial f}{\partial x_i}\).

The classical model for the process is as follows.

Problem \(P\). Find a displacement field \(\boldsymbol{u}:\Omega\times[0,T]\to\mathbb{R}^d\), a stress field \(\boldsymbol{\sigma}:\Omega\times[0,T]\to\mathbb{S}^d\), an electric potential field \(\varphi:\Omega\times[0,T]\to\mathbb{R}\) and an electric displacement field \(\boldsymbol{D}:\Omega\times[0,T]\to\mathbb{R}^d\) such that

In (1)-(12) and below, in order to simplify the notation, we do not indicate explicitly the dependence of various functions on the spatial variable \(\boldsymbol{x}\in \Omega\cup\Gamma\) and the time variable \(t\in [0,T], \) where \(T>0\).

Equations (1) and (2) represent the electro-viscoelastic constitutive law of the material in which denotes \(\boldsymbol{\sigma}=(\sigma_{ij})\) the stress tensor, \(\boldsymbol{\varepsilon(u)}=(\varepsilon_{ij}(\boldsymbol{u}))\) denotes the linearized strain tensor, \(\boldsymbol{\mathcal{E}}(\varphi)\) is the electric field. We recall that \(\varepsilon_{ij}(\boldsymbol{u})=(u_{i,j} + u_{j,i})/2\) and \(\boldsymbol{\mathcal{E}}(\varphi)= – \nabla\varphi=-(\varphi_{,i})\). \({\mathcal{A}}\; {\mathcal{B}}\; {\mathcal{\mathcal{E}}}\) and \(\boldsymbol{\eta}\) are respectively, the viscosity, elasticity, piezoelectric and permittivity tensors. \({\mathcal{\mathcal{E}}}^*\) is the transpose of \({\mathcal{\mathcal{E}}}\). Also the tensors \({\mathcal{\mathcal{E}}}\) and \({\mathcal{\mathcal{E}}}^*\) satisfy the equality \({\mathcal{E}}\boldsymbol{\sigma}\cdot\boldsymbol{v}=\boldsymbol{\sigma}\cdot{\mathcal{\mathcal{E}}}^*\boldsymbol{v}\) for all \(\boldsymbol{\sigma}\in\mathbb{S}^d,\, \boldsymbol{v}\in\mathbb{R}^d,\) and the components of the tensor \({\mathcal{\mathcal{E}}}^*\) are given by \(e_{ijk}^*=e_{kij}\). Equations (3) and (4) are the steady equations for the stress and electric-displacement fields, respectively, in which \({}^{“}\;Div^{“}\) and \({}^{“}\;div^{“}\) denote the divergence operators for tensor and vector valued functions, i.e. \(Div\boldsymbol{\sigma}=(\sigma_{ij,j}),\, div\boldsymbol{D}=(D_{i,i})\). We use these equations since the process is assumed to be mechanically quasistatic and electrically static. Conditions (5) and (6) are the displacement and traction boundary conditions, whereas (7) and (8) represent the electric boundary conditions; these conditions model the fact that the displacement field and the electrical potential vanish on \(\Gamma_D\) and \(\Gamma_a\), respectively, while the forces and the electric charges are prescribed on \(\Gamma_N\) and \(\Gamma_b\) respectively.

We turn to the boundary conditions (9)-(11) which describes the mechanical and electrical conditions on the potential contact surface \(\Gamma_C\). Condition (9) represents the normal compliance contact condition in which \(p_\nu\) is a given function; such that \(p_\nu(r) = 0\) when \(r \leq 0\), \(g\) is the initial gap and the condition, \(u_\nu – g \geq 0\) represents the penetration of body in the foundation. As an example, we may use \(p_\nu(r) = c_\nu r_{+},\) where \(c_\nu\) is a positive constant and \(r_{+} = \max\{r, 0\}\). Condition (10) represents the associated friction law where \(p_\tau\) is a given function. According to (10) the tangential shear cannot exceed the maximum frictional resistance \(p_\tau(u_\nu – g)\), the so-called friction bound. Moreover, when sliding commences, the tangential shear reaches the friction bound and it is opposite to the slip. When we choose \(p_\tau = \mu p_\nu\), we obtain the usual Coulomb law, where \(\mu\geq 0\) is the coefficient of friction. Conditions (9) and (10), were used in several studies as in [10].

Condition (10) is a regularized electrical contact condition on \(\Gamma_C\), similar to that already used in [3,5]. Here \(\psi\) represents the electrical conductivity coefficient, which vanish when its argument is negative, and \(\phi_L\) is a given function and, therefore, in applications \(\phi_L(\varphi -\varphi_f) = \varphi -\varphi_f\). Thus, condition (10) shows that when there is no contact at a point on the surface (i.e. when \(u_\nu< g\)) then the normal component of the electric displacement field vanishes, and when there is contact (i.e. when \(u_\nu\geq g\)) then there may be electrical charges which depend to the difference between the potential of the foundation \(\varphi_f\) and the body's surface potential. Finally, the initial displacement \(\boldsymbol{u}_0\) in (12) is given.

To present the variational formulation of Problem \(P\) we need some additional notation and preliminaries. We start by introducing the spaces

\begin{eqnarray*} && H=L^2(\Omega;\mathbb{R}^d), \quad {\mathcal{H}}=\{\ \boldsymbol{\tau}=(\tau_{ij}):\ \tau_{ij}=\tau_{ji}\in L^2(\Omega)\ \}=L^2(\Omega;\mathbb{S}^d),\\ && H_1 = \{\ \boldsymbol{u} \in H:\ \boldsymbol{\varepsilon(u)}\in {\mathcal{H}}\ \}= H^1(\Omega;\mathbb{R}^d) ,\quad {\mathcal{H}}_1=\{\ \boldsymbol{\tau}\in{\mathcal{H}}:\ Div\boldsymbol{\tau} \in H\ \},\\ &&{\mathcal{w}}=\{ \boldsymbol{D}\in H:\ div \boldsymbol{D} \in L^2(\Omega)\ \}. \end{eqnarray*}

The spaces \(H\), \({\mathcal{H}}\), \(H_1\), \({\mathcal{H}}_1\) and \({w}\), are Hilbert spaces equipped with the inner products \begin{eqnarray*} (\boldsymbol{u,v)}_{H}&=&\int_\Omega \boldsymbol{u}\cdot\boldsymbol{v}\,dx,\\ (\boldsymbol{\sigma},\boldsymbol{\tau})_{\mathcal{H}}&=&\int_\Omega \boldsymbol{\sigma}\cdot\boldsymbol{\tau}\,dx,\\ \boldsymbol{(u,v)}_{H_1}&=&\boldsymbol{(u,v)}_{H}+ (\boldsymbol{\varepsilon(u),\varepsilon(v))}_{\mathcal{H}},\\ (\boldsymbol{\sigma},\boldsymbol{\tau})_{{\mathcal{H}}_1}&=&(\boldsymbol{\sigma},\boldsymbol{\tau})_{\mathcal{H}}+(\mbox{Div}\,\boldsymbol{\sigma}, \mbox{Div}\,\boldsymbol{\tau})_{H},\\ \boldsymbol{(D,E)}_{w}&=&\boldsymbol{(D,E)}_{H}+ (div \boldsymbol{D},\div E)_{L^2(\Omega)}. \end{eqnarray*}

The associated norms in \(H\), \({\mathcal{H}}\), \(H_1\), \({\mathcal{H}}_1\) and \(W\) are denoted by \(\|\cdot\|_{H}\), \(\|\cdot\|_{\mathcal{H}}\), \(\|\cdot\|_{H_1}\), \(\|\cdot\|_{{\mathcal{H}}_1}\) and \(\|\cdot\|_{{w}}\), respectively.

For the displacement and the electric potential fields we introduce the spaces

\[ V=\{\ \boldsymbol{v}\in H^1(\Omega;\mathbb{R}^d)\ |\ \boldsymbol{v} =\boldsymbol{0}\ \mbox{on }\Gamma_{D} \ \},\quad\text{and}\quad W=\{\ \psi \in H^1(\Omega)\ |\ \psi = 0\ \mbox{on}\ \Gamma_a\ \} \] which are closed subspaces of \(H_1\) and \(H^1(\Omega)\), respectively. On \(V\) and \(W\) we consider the inner products and the corresponding norms given by \[ \boldsymbol{(u,v)}_V=\boldsymbol{(\varepsilon(u),\varepsilon(v))}_{\mathcal{H}},\quad \|\boldsymbol{v}\|_V = \|\boldsymbol{\varepsilon(v)}\|_{\mathcal{H}} \quad \mbox{for all } \boldsymbol{u},\ \boldsymbol{v}\in V, \] \[ (\varphi,\psi)_W=(\nabla\varphi,\nabla\psi)_{H},\quad \|\psi\|_W = \|\nabla\psi\|_{ H} \quad \mbox{for all } \varphi,\ \psi\in W. \] Since \(meas\,(\Gamma_D)>0\) and meas \(meas\,(\Gamma_a)>0\) are positive, it follows from the Korn and the Friedrichs-Poincaré inequalities, respectively, that \((V,\|\cdot\|_V)\) and \((W,\|\cdot\|_W)\) are Hilbert spaces.

We now list the assumptions on the problem’s data. We assume that the viscosity tensor \({A} :\Omega\times\mathbb{S}^d\to \mathbb{S}^d\) and the elasticity tensor \( {B} :\Omega\times\mathbb{S}^d\to \mathbb{S}^d\) satisfy

The piezoelectric tensor \({\mathcal{\mathcal{E}}}\) and the electric permittivity tensor \(\boldsymbol{\beta}\) satisfy The normal compliance functions \( p_r,\, (r=\nu,\tau)\) satisfy The surface electrical conductivity function \(\psi\) satisfies: The following regularity is assumed on the density of volume forces, tractions, volume electric charge and surface electric charges: Finally, we assume that the gap function, the given potential of the foundation and the initial displacements satisfy Next, we can define the element \(\boldsymbol{f} : [0,T]\longrightarrow V\) given by \begin{equation*} (\boldsymbol{f}(t), \boldsymbol{w})_{V}=\int_\Omega \boldsymbol{f}_0(t)\cdot\boldsymbol{w}\,dx+\int_{\Gamma_N} \boldsymbol{f}_N(t)\cdot\boldsymbol{w}\,da, \end{equation*} and then \(\boldsymbol{f}\in W^{1,1}(0,T; V)\).

Using the Riesz’ Theorem, we define the linear mapping \(q : [0,T]\longrightarrow W\) as follows:

\begin{equation*} (q(t), \psi)_W= -\int_\Omega q_0(t)\psi\,dx-\int_{\Gamma_b} q_b(t)\psi\,da\quad\forall \psi\in W. \end{equation*} We notice that the regularity assumptions imply that \(q\in W^{1,1}(0,T; W)\).

Let \(\;j : V\times V\longrightarrow {\mathbb R}\) and \(\;K : V\times W\times W\longrightarrow R\) be the mapping defined by

\begin{eqnarray*} &&j(\boldsymbol{v},\boldsymbol{w})=\int_{\Gamma_C} [ p_\nu(v_\nu – g)w_\nu\, + \, p_\tau(\boldsymbol{v}_\tau – g)\|\boldsymbol{w}_{\tau}\|]\,da,\\[1mm] &&K(\boldsymbol{u},\varphi,\psi) = \int_{\Gamma_C} \psi(u_\nu – g)\phi_L(\varphi – \varphi_f)\psi\,da, \end{eqnarray*} for all \(\boldsymbol{w}\in V, \) and \(\psi\in W\).

Plugging (1) into (3) and (2) into (4), keeping in mind that \(\boldsymbol{\mathcal{E}}(\varphi)=-\nabla\varphi\) and using the boundary conditions (5)-(11) and the initial condition (12), applying a Green’s formula we derive the following variational formulation of Problem \(P\) in terms of the displacement and the electric potential fields.

Problem \(P_V\). Find a displacement field \(\boldsymbol{u}:[0, T]\to V\) and an electric potential field \(\varphi:[0, T]\to W\) such that \(\;\boldsymbol{u}(0)=\boldsymbol{u}_0\) and for a.e. \(t\in (0,T)\), \begin{eqnarray*} &&({A}\boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)),\boldsymbol{\varepsilon}(\boldsymbol{w}) – \boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)))_{\mathcal{H}} + ({B}\boldsymbol{\varepsilon}(\boldsymbol{u}(t)),\boldsymbol{\varepsilon}(\boldsymbol{w}) – \boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)))_{\mathcal{H}} \\[1mm] && \quad + ({\mathcal{\mathcal{E}}}^*\nabla\varphi(t),\boldsymbol{\varepsilon}(\boldsymbol{w}) – \boldsymbol{\varepsilon}(\dot{\boldsymbol{u}}(t)))_{\mathcal{H}} + j({\boldsymbol{u}}(t),\boldsymbol{w}) – j({\boldsymbol{u}}(t),\dot{\boldsymbol{u}}(t)) \geq (\boldsymbol{f}(t), \boldsymbol{w} – \dot{\boldsymbol{u}}(t))_{V}, \\[1mm] &&(\boldsymbol{\beta}\nabla \varphi(t),\nabla\psi)_{H}-({\mathcal{E}}\boldsymbol{\varepsilon}(\boldsymbol{u}(t)), \nabla \psi)_{H} + K(\boldsymbol{u}(t),\varphi(t),\psi) = (q(t),\psi)_W, \hspace{-0.cm} \end{eqnarray*} for all \(\boldsymbol{w}\in V\) and \(\psi \in W\)}. The following result is proved in [1].

Theorem 1. Assume that (13)-(20) hold. Then there exists a unique solution \((\boldsymbol{u},\varphi)\) to Problem \(P_V\) with the regularity \(\boldsymbol{u}\in\,W^{2,1}(0,T; V),\; \varphi\in W^{1,1}(0,T; W)\).

3. Numerical analysis

We now introduce a fully discrete scheme to approximate the solution of Problem \(P_V\). First, we consider two finite dimensional spaces \(V^h\subset V\) and \(W^h\subset W\) approximating the spaces \(V\) and \(W\), respectively. \(h>0\) denotes the spatial discretization parameter. Secondly, the time derivatives are discretized by using a uniform partition of \([0,T]\), denoted by \(0=t_0< t_1 < \ldots< t_N=T\). Let \(k\) be the time step size, \(k=T/N\), and for a continuous function \(f(t)\) let \(f_n=f(t_n)\). Finally, for a sequence \(\{w_n\}_{n=0}^N\) we denote by \(\delta w_n=(w_n-w_{n-1})/k\) the divided differences.

The fully discrete approximation of Problem \(P_V\), based on the forward Euler scheme, is the following.

Problem \(P_V^{hk}\). Find a discrete displacement field \(\boldsymbol{u}^{hk}=\{\boldsymbol{u}_n^{hk}\}_{n=0}^N\subset V^h\) and a discrete electric potential field \(\varphi^{hk}=\{\varphi_n^{hk}\}_{n=0}^N\subset W^h\) such that \(\boldsymbol{u}_0^{hk}=\boldsymbol{u}_0^h\) and for all \(n=1,\ldots,N\), \begin{eqnarray*} && ({\mathcal{A}}\boldsymbol{\varepsilon}({\delta\boldsymbol{u}}_{n}^{hk}),\boldsymbol{\varepsilon}(\boldsymbol{w}^h) – \boldsymbol{\varepsilon}(\delta{\boldsymbol{u}}_{n}^{hk}))_{\mathcal{H}} + ({B}\boldsymbol{\varepsilon}(\boldsymbol{u}_{n}^{hk}),\boldsymbol{\varepsilon}(\boldsymbol{w}^h) – \boldsymbol{\varepsilon}(\delta{\boldsymbol{u}}_{n}^{hk}))_{\mathcal{H}} \\[1mm] && + ({\mathcal{\mathcal{E}}}^*\nabla\varphi_{n}^{hk},\boldsymbol{\varepsilon}(\boldsymbol{w}^h) – \boldsymbol{\varepsilon}(\delta{\boldsymbol{u}}_{n}^{hk}))_{\mathcal{H}}+ j({\boldsymbol{u}}_{n}^{hk},\boldsymbol{w}^h) – j({\boldsymbol{u}}_{n}^{hk},\delta{\boldsymbol{u}}_{n}^{hk}) \geq (\boldsymbol{f}_n, \boldsymbol{w}^h – \delta{\boldsymbol{u}}_{n}^{hk})_{V}\quad\forall \,\boldsymbol{w}^h\in V^h, \\[1mm] && (\boldsymbol{\eta}\nabla \varphi_{n}^{hk},\nabla\psi^h)_{H}-({\mathcal{E}}\boldsymbol{\varepsilon}(\boldsymbol{u}_{n}^{hk}), \nabla \psi^h)_{H} + K(\boldsymbol{u}_{n}^{hk},\varphi_{n}^{hk},\psi^h) = (q_n,\psi^h)_W\quad \forall\,\psi^h \in W^h. \end{eqnarray*}

Here \(\boldsymbol{u}_0^h\) is appropriate approximation of the initial condition \(\boldsymbol{u}_0\) and \(\varphi_0^{hk}\) is the unique solution of the second equation in Problem \(P_V^{hk}\) for \(n=0\).

Using the assumptions of Theorem 1, it can shown that Problem \(P_V^{hk}\) has a unique solution \((\boldsymbol{u}^{hk},\varphi^{hk})\in V^h\times W^h\). Now, we proceed to derive some error estimates for the discrete solution. In the sequel, \(c\) denotes positive constants which are independent of the discretization parameters \(h\) and \(k\).

Theorem 2. Assume the conditions of Theorem 1 hold. One has the following error estimates:

where \[ R_n(\dot{\boldsymbol{u}}_n , \boldsymbol{w}_n^{h}) = (\boldsymbol{\sigma}_n,\boldsymbol{v}arepsilon(\boldsymbol{w}_n^h – \dot{\boldsymbol{u}}_n))_{\mathcal{H}} + j({\boldsymbol{u}}_{n},\boldsymbol{w}_n^h) – j({\boldsymbol{u}}_{n},\dot{\boldsymbol{u}}_{n}) – (\boldsymbol{f}_n, \boldsymbol{w}_n^h – \dot{\boldsymbol{u}}_{n})_{V}. \]

Proof. We follow the technics developed in (see [10] and [7]). The reader is invited to consult the mentioned thesis for details.

We notice that the above error estimates are the basis for the analysis of the convergence rate of the algorithm. Thus, let \(\Omega\) be a polygonal domain and let \({T}^h\) a regular finite element partition of \(\Omega\). Let \(V^h\subset V\) and \(W^h\subset W\) be the finite element space consisting of continuous and piecewise affine functions, corresponding to the partition \({T}^h\). Assume that the discrete initial condition \(\boldsymbol{u}_0^h\) is obtained by \(\boldsymbol{u}_0^h=\Pi^h\boldsymbol{u}_0\), where \(\Pi^h=(\pi^h)_{i=1}^d:[C(\overline{\Omega})]^d\rightarrow V^h\), and \(\pi^h \) is the standard finite element interpolation operator (see, e.g., [11]).

We assume the following additional data and solution regularities: By the relations (3) and (6) and using a Green’s formula, we have \begin{eqnarray*} && R_n(\dot{\boldsymbol{u}}_n , \boldsymbol{w}_n^{h}) = \displaystyle\int_{\Gamma_C}\Big(\boldsymbol{\sigma}_{\tau_n}\cdot(\boldsymbol{w}_{\tau_n}^h – \dot{\boldsymbol{u}}_{\tau_n}) + (p_\tau(u_{\nu_n} – g^h)(|\boldsymbol{w}_{\tau_n}^h| – |\dot{\boldsymbol{u}}_{\tau_n}|)\Big)\, da, \end{eqnarray*} which implies that \begin{eqnarray*} && |R_n(\dot{\boldsymbol{u}}_n , \boldsymbol{w}_n^{h})| \leq c\| \boldsymbol{w}_{\tau_n}^h – \dot{\boldsymbol{u}}_{\tau_n} \|_{L^2(\Gamma_C)^d}. \end{eqnarray*} Thus, from (21), we obtain \begin{eqnarray*} &&\displaystyle \max_{0\leq n\leq N} \Big( \|\boldsymbol{u}_n-\boldsymbol{u}_n^{hk}\|_{V} + \|\dot{\boldsymbol{u}}_n-\delta\boldsymbol{u}_n^{hk}\|_{V} + \|\varphi_n-\varphi_n^{hk}\|_W \Big)\\ && \leq c \max_{0\leq n\leq N} \Big\{ \|\dot{\boldsymbol{u}}_n-\boldsymbol{w}_n^{h}\|_{V} + \| \boldsymbol{w}_{\tau_n}^h – \dot{\boldsymbol{u}}_{\tau_n} \|_{L^2(\Gamma_C)^d}^{1/2}\Big\} + c\max_{0\leq n\leq N} \Big\{ \|\varphi_n-\psi_n^{h}\|_W \Big\} + c \|\boldsymbol{u}_0-\boldsymbol{u}_0^h\|_V + c k \|\dot{\boldsymbol{u}}\|_{W^{1,1}(0,T; V)}. \end{eqnarray*} Under the solution regularity assumptions (22)-(24), we can apply standard finite element interpolation error estimates (see e.g., [11]) to see that each of the terms \[ \|\boldsymbol{u}_0-\boldsymbol{u}_0^h\|_V, \; \max_{0\leq n\leq N} \Big\{ \|\dot{\boldsymbol{u}}_n-\boldsymbol{w}_n^{h}\|_{V} + \| \boldsymbol{w}_{\tau_n}^h – \dot{\boldsymbol{u}}_{\tau_n} \|_{L^2(\Gamma_C)^d}^{1/2}\Big\} \;\mbox{ and }\; \max_{0\leq n\leq N} \Big\{ \|\varphi_n-\psi_n^{h}\|_W \Big\} \] is bounded by \(h\) multiplied by a constant depending on certain norm of the solution. Hence, we get the following error bound for the fully discrete numerical solution of Problem \(P_V\):

4. Numerical algorithm

In this section, we present first the numerical scheme which we have implemented. Then, we describe two-dimensional example of the numerical results, that we obtained by employing it, to show the performance of the method.

4.1. Numerical scheme

We now turn to a hybrid variational formulation of the model which is more appropriate for the numerical modelling. To this end, we consider the space of traces \(X = \{{\boldsymbol{w_\tau}}_{|_{\Gamma_C}}\, :\, \boldsymbol{w} \in V \}\), together with his dual \(X^{‘}\), and let \(Y^h\subset X^{‘} \cap L^2(\Gamma_C)\) be a discrete multiplier space. Then, using the arguments in [12], it follows that Problem \(P_V^{hk}\) is equivalent with the following hybrid formulation, in which the multiplier \(\boldsymbol{\lambda}^{hk}\) represents the tangential stress on the contact boundary.

Problem \(\tilde{P}_V^{hk}\). Find a discrete displacement field \(\boldsymbol{u}^{hk}=\{\boldsymbol{u}_n^{hk}\}_{n=0}^N\subset V^h\), a discrete multiplier \(\boldsymbol{\lambda}^{hk} = \{\boldsymbol{\lambda}_n^{hk}\}_{n=0}^N \subset Y^h\) and a discrete electric potential field \(\varphi^{hk}=\{\varphi_n^{hk}\}_{n=0}^N\subset W^h\) such that, for all \(n=1,\ldots,N\),}

\begin{eqnarray}\label{friction2} && ({\mathcal{A}}\boldsymbol{\varepsilon}({\delta\boldsymbol{u}}_{n}^{hk}),\boldsymbol{\varepsilon}(\boldsymbol{w}^h))_{\mathcal{H}} + ({\mathcal{B}}\boldsymbol{\varepsilon}(\boldsymbol{u}_{n}^{hk}),\boldsymbol{\varepsilon}(\boldsymbol{w}^h))_{\mathcal{H}}+ ({\mathcal{\mathcal{E}}}^*\nabla\varphi_{n}^{hk},\boldsymbol{\varepsilon}(\boldsymbol{w}^h))_{\mathcal{H}} + J({\boldsymbol{u}}_{n}^{hk},\boldsymbol{\lambda}_{n}^{hk},\boldsymbol{w}^h) = (\boldsymbol{f}_n, \boldsymbol{w}^h)_{V}\quad\forall \,\boldsymbol{w}^h\in V^h, \nonumber \\[1mm] && (\boldsymbol{\eta}\nabla \varphi_{n}^{hk},\nabla\psi^h)_{H}-({\mathcal{E}}\boldsymbol{\varepsilon}(\boldsymbol{u}_{n}^{hk}), \nabla \psi^h)_{H} + K({\boldsymbol{u}}_{n}^{hk},\varphi_{n}^{hk},\psi^h) = (q_n,\psi^h)_W\\&&\nonumber \forall\,\psi^h \in W^h, -\boldsymbol{\lambda}_{n}^{hk}\in \partial I_{C[p_\tau(u_{{\nu}_{n}}^{hk} – g^h )]}^{*}( {\delta\boldsymbol{u}}_{{\tau}_{n}}^{hk})\; \mbox{ in }\; Y^{h}. \end{eqnarray}

(26)

The inclusion (26) represents the subdifferential form of Coulomb’s law of dry friction (10). Here \(C[ p_\tau(u_{{\nu}_{n}}^{hk} – g^h )]\) denotes the ball radius \( p_\tau(u_{{\nu}_{n}}^{hk} – g^h )\) where \(g^h\) represents an appropriate approximation of the gap and \(\partial I_S^{*}\) denotes the subdifferential of the conjugate of the indicator function of the set S. In Problem \(\tilde{P}_V^{hk}\) the contact functional term \(J({\boldsymbol{u}}_{n}^{hk},\boldsymbol{\lambda}_{n}^{hk},\boldsymbol{w}^h)\) is defined by \[ J({\boldsymbol{u}}_{n}^{hk},\boldsymbol{\lambda}_{n}^{hk},\boldsymbol{w}^h) = \int_{\Gamma_C} p_\nu(u_{{\nu}_{n}}^{hk} – g^h)w_\nu^h\,da + \int_{\Gamma_C} \boldsymbol{\lambda}_{n}^{hk}\cdot\boldsymbol{w_\tau}^h\,da. \] The numerical treatment of the frictional contact of Problem \(\tilde{P}_V^{hk}\), is based on the use of a penalized method for the contact part and the augmented Lagrangian method for the non-smooth friction. To this end we consider additional fictitious nodes for the Lagrange multiplier in the initial mesh. The construction of these nodes depends on the contact element used for the geometrical discretization of the interface \(\Gamma_C\). In the case of the numerical example presented in Section 4.2, the discretization is based on “node-to-rigid” contact element, which is composed by one node of \(\Gamma_C\) and one Lagrange multiplier node. This contact interface discretization is characterized by a finite dimensional subspace \(H_{\Gamma_C}^h \subset Y^h\). Let \(N_{tot}\) be the total number of nodes and denote by \(\alpha^i\), \(\beta^i\) the basis functions of the space \(V^h\) and \(W^h\), respectively, for \(i=1,\ldots,N_{tot}\). Moreover, let \(N_{\Gamma_C}\) represent the number of nodes on the interface \(\Gamma_C\) and let \(\mu^i\) be the shape functions of the finite element space \(H_{\Gamma_C}^h\), for \(i = 1,\cdots, N_{\Gamma_C}\); so, \(H_{\Gamma_C}^h = \{\gamma_h \in Y^h\, :\, \gamma_h = \sum_{i=1}^{N_{\Gamma_C}} \gamma^i\mu^i\}\). Usually, if a \(P_1\) finite element method is used for the displacement, then a \(P_0\) finite element method is considered for the multipliers. Then, the expressions of the functions \(\boldsymbol{w}^{h},\, \psi^h\) and \(\boldsymbol{\gamma}^{h}\) is given by \(\boldsymbol{w}^h =\displaystyle \sum_{i=1}^{N_{tot}}\boldsymbol{w}^i\alpha^i, \; \psi^h = \displaystyle\sum_{i=1}^{N_{tot}}\psi^i\beta^i,\; \gamma^h = \displaystyle\sum_{i=1}^{N_{\Gamma_C}}\gamma^i\mu^i, \) where \(\boldsymbol{w}^i\) and \(\psi^i\) represent the values of the coreesponding functions \(\boldsymbol{w}^h\) and \(\psi^h\) at the \(i^{th}\) node of \({\mathcal T}^h\). Also, \(\gamma^i\) denotes the values of the function \(\gamma^h\) at the \(i^{th}\) node of the contact element discretization of the contact interface. More details about this discretization step can be found in [8,9] for details.

The augmented Lagrangian approach we use shows that the Problem \(\tilde{P}_V^{hk}\) can be governed by the following system of nonlinear equations

that we describe below. First, the vectors \(\delta\boldsymbol{u}_n\), \(\boldsymbol{u}_n\), \(\varphi_n\) and \(\boldsymbol{\lambda}_n\) represent the velocity, the displacement, the electric potential and the Lagrange multiplier generalized vectors, respectively, defined by \begin{equation*} \delta\boldsymbol{u}_n = \{\delta\boldsymbol{u}^i_n\}_{i=1}^{N_{tot}}, \ \boldsymbol{u}_n = \{\boldsymbol{u}^i_n\}_{i=1}^{N_{tot}}, \ \varphi_n = \{\varphi^i_n\}_{i=1}^{N_{tot}}\ \mbox{ and }\ \boldsymbol{\lambda}_n = \{\boldsymbol{\lambda}^i_n\}_{i=1}^{N_{\Gamma_C}}, \end{equation*} where \(\delta\boldsymbol{u}^i_n : = \displaystyle\frac{\boldsymbol{u}_n^i – \boldsymbol{u}_{n-1}^i}{k},\; \boldsymbol{u}^i_n\) and \(\varphi^i_n\) represent the values of the corresponding functions \(\delta\boldsymbol{u}^{hk}_n\), \(\boldsymbol{u}^{hk}_n\) and \(\varphi^{hk}_n\) at the \(i^{th}\) node of \({\mathcal T}^h\). Also, \(\boldsymbol{\lambda}_n^i\) denote the values of the corresponding function \(\boldsymbol{\lambda}_n^{hk}\) at the \(i^{th}\) node of the contact element of the discretized contact interface.

Next, the generalized viscous term \(\tilde{\boldsymbol{A}}(\boldsymbol{v})\in \mathbb{R}^{d\times N_{tot} }\times{\mathbb{R}^{N_{tot} }}\times{\mathbb{R}^{d\times N_{\Gamma_C} }}\) and the generalized electro-elastic term \(\tilde{\boldsymbol{G}}(\boldsymbol{u}, \,\varphi)\in \mathbb{R}^{d\times N_{tot} }\times{\mathbb{R}^{N_{tot} }}\times{\mathbb{R}^{d\times N_{\Gamma_C} }}\) are defined by \(\tilde{\boldsymbol{A}}(\boldsymbol{v})=({\boldsymbol{A}}(\boldsymbol{v}),\boldsymbol{0}_{N_{tot}}, \boldsymbol{0}_{d\times N_{\Gamma_C}})\) and \(\tilde{\boldsymbol{G}}(\boldsymbol{u}, \,\varphi)=({\boldsymbol{G}}(\boldsymbol{u}, \,\varphi),\boldsymbol{0}_{d\times N_{\Gamma_C}})\). Here, \(\boldsymbol{0}_{N_{tot}}\) is the zero element of \(\mathbb{R}^{ N_{tot}}\) and \(\boldsymbol{0}_{d\times N_{\Gamma_C}}\) is the zero element of \(\mathbb{R}^{ d\times N_{\Gamma_C}}\) ; also, \({\boldsymbol{A}}(\boldsymbol{v})\in\mathbb{R}^{d\times N_{tot} }\), \({\boldsymbol{G}}(\boldsymbol{u}, \, \varphi)\in {{\mathbb{R}^{d\times N_{tot} }}\times{\mathbb{R}^{N_{tot} }}}\) denote the viscous term and the elastic-piezoelectric term, respectively, given by

\begin{eqnarray}\label{7.3} && ({\boldsymbol{A}}(\boldsymbol{v}) \cdot \boldsymbol{w})_{\mathbb{R}^{d\times N_{tot}}} = ({A}\boldsymbol{\varepsilon}(\boldsymbol{v}^h), \boldsymbol{\varepsilon}(\boldsymbol{w}^h))_{\mathcal{H}} \quad \forall \boldsymbol{v},\,\boldsymbol{w} \in{\mathbb{R}^{d\times N_{tot}}},\;\forall \boldsymbol{v}^h,\,\boldsymbol{w}^h \in V^h \nonumber, \\[1 mm] &&({\boldsymbol{G}}(\boldsymbol{u}, \, \varphi) \cdot (\boldsymbol{w},\psi))_{{\mathbb{R}^{d\times N_{tot} }}\times{\mathbb{R}^{N_{tot} }}} = (B\boldsymbol{\varepsilon}(\boldsymbol{u}^h), \boldsymbol{\varepsilon}(\boldsymbol{w}^h))_{\mathcal{H}} + (E\boldsymbol{\varepsilon}(\boldsymbol{w}^h), \nabla\varphi^h)_H – (\boldsymbol{n},\boldsymbol{w}^h)_V – (E\boldsymbol{\varepsilon}(\boldsymbol{u}^h) \nonumber \\[1 mm] &&- \beta\nabla\varphi^h , \nabla\psi^h)_H – (q_n,\psi^h)_W, \;\; \forall \boldsymbol{u},\,\boldsymbol{w} \in{\mathbb{R}^{d\times N_{tot}}},\;\forall \varphi,\, \psi \in{\mathbb{R}^{ N_{tot}}},\;\forall \boldsymbol{u}^h,\,\boldsymbol{w}^h \in V^h,\; \forall \varphi^h,\,\psi^h \in W^h. \nonumber \end{eqnarray} Above, \(\boldsymbol{v},\,\boldsymbol{u},\,\boldsymbol{w},\,\varphi\) and \(\psi\) represent the generalized vectors of components \(\boldsymbol{v}^i,\,\boldsymbol{u}^i,\,\boldsymbol{w}^i,\,\varphi^i\) and \(\psi^i\) for \(i=1,\ldots,N_{tot}\), respectively, and note that the volume and surface efforts are contained in the term \({\boldsymbol{G}}(\boldsymbol{u}, \, \varphi)\). Finally, The contact operator \({\boldsymbol{F}}(\boldsymbol{u},\varphi,\boldsymbol{\lambda})\), which permits to take into account the conductivity of the foundation, is given by \begin{eqnarray*} &&\label{3.1121} ({\boldsymbol{F}}(\boldsymbol{u},\varphi,\boldsymbol{\lambda}),(\boldsymbol{w},\psi,\boldsymbol{\gamma}))_{{\mathbb R}^{d\times N_{tot} }\times{{\mathbb R}^{N_{tot} }}\times{{\mathbb R}^{d\times N_{\Gamma_C} }}} = \int_{\Gamma_C} p_\nu(u_{{\nu}}^{h} – g^h)w_\nu^h\,da \nonumber \\[1 mm] && + \displaystyle\int_{\Gamma_{C}}\nabla_{\small \boldsymbol{u}} l_{\tau}^{r}(\boldsymbol{u}^{h},\boldsymbol{\lambda}^{h}).\boldsymbol{w}^{h}\ da + \displaystyle\int_{\Gamma_{C}}\nabla_{\small \boldsymbol{\lambda}} l_{\tau}^{r}(\boldsymbol{u}^{h},\boldsymbol{\lambda}^{h}).\boldsymbol{\gamma}^{h} \ da + K(\boldsymbol{u}^h,\varphi^h,\psi^h),\\ && \forall\, \boldsymbol{u}, \boldsymbol{w}\in \mathbb{R}^{d\times N^{h}_{tot}},\, \forall\, \varphi, \psi\in \mathbb{R}^{N^{h}_{tot}},\, \forall\,\boldsymbol{\lambda}, \boldsymbol{\gamma}\in \mathbb{R}^{d\times N^{h}_{\Gamma_C}}, \forall \boldsymbol{u}^{h},\, \boldsymbol{w}^h\in V^{h}, \;\forall \varphi^{h},\, \psi^h\in W^{h}, \;\forall\,\boldsymbol{\lambda}^h,\, \boldsymbol{\gamma}^{h}\in Y^{h}. \end{eqnarray*} Here the Lagrangian multiplier \(\boldsymbol{\lambda}\) represents the friction force and \(\boldsymbol{\gamma}\) is a test function; also, \( l_\tau^r\) denote the augmented Lagrangian functional given by \begin{equation*} l_{\tau}^{r}(\boldsymbol{u}^{h},\boldsymbol{\lambda}^{h}) =\delta\boldsymbol{u}_{\tau}^{h}\cdot \boldsymbol{\lambda}^{h} + \displaystyle\frac{r}{2}|\delta\boldsymbol{u}_{\tau}^{h}|^{2} – \displaystyle\frac{1}{2r}dist^{2}\{\boldsymbol{\lambda}^{h} + r\delta\boldsymbol{u}_{\tau}^{h},C[p_\tau(u_{\nu}^{h} – g^h)]\} \end{equation*} where \(r\) is positive penalty coefficient and the Coulomb convex set \(C[p_\tau(u_{\nu}^{h} – g^h)]\) denotes the convex disk of constant radius \(p_\tau(u_{\nu}^{h} – g^h)\). For more details about the Lagrangian method, we refer the reader to [8,9].

The solution algorithm consists in a prediction-correction scheme based on a finite differences method (the backward Euler difference method) and a linear iterations methods (the Newton method). The finite difference scheme we use is characterized by a first order time integration scheme, both for the velocity \(\boldsymbol{v}_n = \delta\boldsymbol{u}_n\). To solve (27), at each time increment the variables \((\boldsymbol{u}_n,\,\varphi_n,\,\boldsymbol{\lambda}_n)\) are treated simultaneously through a Newton method and, for this reason, we use in what follows the notation \({\boldsymbol{x}}_n = (\boldsymbol{u}_n,\,\varphi_n,\,\boldsymbol{\lambda}_n)\).

Inside the loop of the increment time indexed by \(n\), the algorithm we use can be developed in three steps which are the following.

\({\boldsymbol{F}or}\) \(n=0\) until \(N\), let \(\varphi_0,\,\boldsymbol{u}_0,\,\delta\boldsymbol{u}_0\) and \(\boldsymbol{\lambda}_0\) be given or chosen in an appropriate way.

• A prediction step: This step provides the initial values \(\varphi_{n+1}^0, \ \boldsymbol{u}_{n+1}^0, \ \delta\boldsymbol{u}_{n+1}^0 \) and \( \boldsymbol{\lambda}_{n+1}^0 \) by the formulas: \(\;\varphi_{n+1}^0 = \varphi_{n}, \; \boldsymbol{u}_{n+1}^0 = \boldsymbol{u}_{n}, \; \delta\boldsymbol{u}_{n+1}^0 = \boldsymbol{0} \; \mbox{and} \; \boldsymbol{\lambda}_{n+1}^0 = \boldsymbol{\lambda}_{n}.\)
• A Newton linearization step: for \(i=0\) until convergence, compute
\begin{align*} & {\boldsymbol{x}}^{i+1}_{n+1} = {\boldsymbol{x}}^{i}_{n+1}-\left(\displaystyle\frac {\boldsymbol{Q}^{i}_{n+1}} {k}+ {\boldsymbol{K}}^{i}_{n+1} + \boldsymbol{T}^{i}_{n+1}\right)^{-1} {\boldsymbol{ R}}\left(\delta\boldsymbol{u}_{n+1}^i , \boldsymbol{u}_{n+1}^i, \varphi_{n+1}^i , \boldsymbol{\lambda}_{n+1}^i \right) \end{align*}

where \({\boldsymbol{x}}^{i+1}_{n+1}\) denotes the pair \((\boldsymbol{u}^{i+1}_{n+1},\,\varphi^{i+1}_{n+1},\,\boldsymbol{\lambda}^{i+1}_{n+1})\); \(i\) and \(n\) represent respectively the Newton iteration index and the time index; \(\boldsymbol{Q}^{i}_{n+1} =D_{\small\boldsymbol{u}}{\boldsymbol{A}}({\boldsymbol{v}}^{i}_{n+1})\) denotes the damping matrix, \(\boldsymbol{K}^{i}_{n+1} = D_{\small\boldsymbol{u},\varphi}{\boldsymbol{G}}(\boldsymbol{u}^{i}_{n+1},\varphi^{i}_{n+1})\) represents the elastic matrix and \(\boldsymbol{T}^{i}_{n+1} = D_{\small\boldsymbol{u},\varphi,\boldsymbol{\lambda}}{{\boldsymbol{F}}}(\boldsymbol{u}^{i}_{n+1},\varphi^{i}_{n+1},\boldsymbol{\lambda}^{i}_{n+1})\) is the contact tangent matrix; also, \(D_{\small\boldsymbol{u}}{\boldsymbol{A}}\), \(D_{\small \boldsymbol{u},\varphi}{\boldsymbol{G}}\) and \(D_{\small\boldsymbol{u},\varphi,\boldsymbol{\lambda}}{{\boldsymbol{F}}}\) denote the differentials of the functions \({\boldsymbol{A}}\), \({\boldsymbol{G}}\) and \({\boldsymbol{F}}\) with respect to the variables \(\boldsymbol{u},\,\varphi\) and \(\boldsymbol{\lambda}\). This leads us to solve the resulting linear system where \(\delta{\boldsymbol{x}}^{i} = (\delta\boldsymbol{u}^{i},\,\Delta\varphi^{i},\,\delta\boldsymbol{\lambda}^{i})\) with \(\delta \boldsymbol{u}^{i} = \boldsymbol{u}^{i+1}_{n+1}-\boldsymbol{u}^{i}_{n+1},\,\delta\varphi^{i} = \varphi^{i+1}_{n+1}-\varphi^{i}_{n+1}\) and \(\Delta \boldsymbol{\lambda}^{i} = \boldsymbol{\lambda}^{i+1}_{n+1}-\boldsymbol{\lambda}^{i}_{n+1}\).

• A correction step: Once the system (28) is resolved, we update \({\boldsymbol{x}}^{i+1}_{n+1}\) and \(\delta\boldsymbol{u}^{i+1}_{n+1}\) by

\begin{align*} & {\boldsymbol{x}}^{i+1}_{n+1} = {\boldsymbol{x}}^{i}_{n+1} + \Delta{\boldsymbol{x}}^{i} \quad \mbox{and} \quad \delta\boldsymbol{u}^{i+1}_{n+1} = \delta\boldsymbol{u}^{i}_{n+1} + \displaystyle\frac{\Delta \boldsymbol{u}^{i}}{k}\, . \end{align*} Note that formulation (27) has been implemented in the open-source finite element library GetFEM++ (see http://getfem.org/).

4.2. Numerical simulations

Now we illustrate our theoretical results by numerical simulations in the study of two-dimensional test problem. In order to observe the effect of the piezoelectric properties of the material, a physical setting as the one depicted in Figure 1 is considered. In this case the body \(\Omega=(0,1)\times(0,1)\subset \mathbb{R}^2\) is clamped on \(\Gamma_{D}= [0,1]\times \{0\}\) and the electric potential is free there (we choose \(\Gamma_{D}= \Gamma_{a}\)). The tractions \(\boldsymbol{f_n}^1(x_1,x_2,t) := (0.8\, t,0.2\, t)\, N/m\) and \(\boldsymbol{f_n}^2(x_1,x_2,t) := (-0.3\, t,0.1\, t)\, N/m\) are prescribed on the lateral parts \(\Gamma_N^1,\, \Gamma_N^2\) respectively (i.e. \(\Gamma_N :=\Gamma_N^1\cup\Gamma_N^2=\Gamma_b\)). The body is in contact with a conductive foundation on its lower boundary \(\Gamma_{C}= [0,1]\times\{0\}\). No volume forces and no electric charges are supposed to act in the body, i.e. \(\boldsymbol{f}_0=\boldsymbol{0}\,\) \(N/m^2\), \(q_0=0\, W/m^2\), \(q_b=0\, W/m\). The functions \(p_\nu\) and \(p_\tau\) in the frictional contact conditions (9) and (10) are given by \(p_\nu(r) = c_\nu r_{+}\) and \(p_\tau = \mu p_\nu\), where \(c_\nu\) represent large positive constant and \(\mu\) represents the friction coefficient. And, finally, The truncation function \(\phi_L\), and the conductivity functions \(\psi\) in the conditions (11) are given by \[ \phi_{L}(s)=s,\qquad \psi(s) = k_e\cdot\left\{ \begin{array}{rl} 0 &\mbox{ if \(s \epsilon_e\)}, \end{array} \right. \] where \(k_e\) and \(\epsilon_e\) are positive constants.

Here, we use as material the visco-elasto-piezoelectric body whose constants are taken as [2,3]. The following data have been used in the numerical simulations: \begin{eqnarray*} && c_\nu=10^{7}\, N /m^2 ,\;\; \mu = 0.1 ,\;\; g=0\,m. \\[1mm] && k_e= 1 ,\;\;\epsilon_e = 10^{-5}\, m,\;\; \varphi_f = 128 \,V,\;\; T=0.1\, s ,\;\; \boldsymbol{u}_0= \boldsymbol{0} \, m. \end{eqnarray*}

Our interest in this example is to study the influence of the electrical conductivity of the foundation on the contact process and, to this end, we consider the problem both in the case when the foundation is insulated (i.e. \( \boldsymbol{D}\cdot \boldsymbol{\nu} = 0\mbox{ on } \Gamma_C\)) and in the case when it is conductive.

Both electric potential and Von Mises stress norm are plotted in Figures 3 at final time for the value \(\varphi_f = 128\, V\).

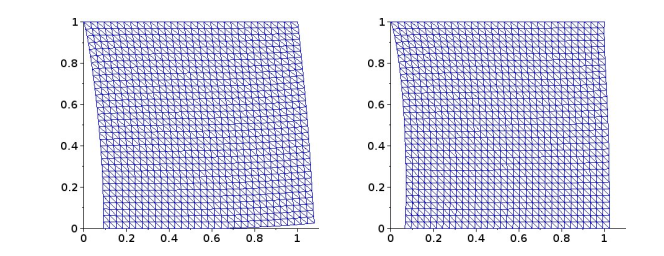
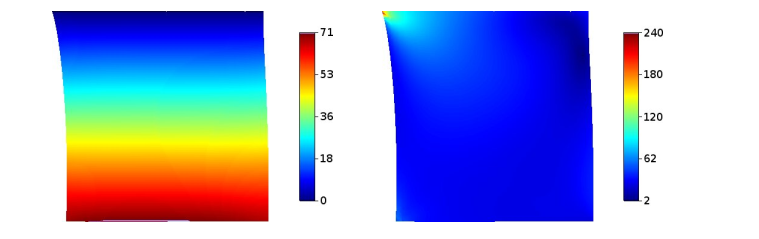
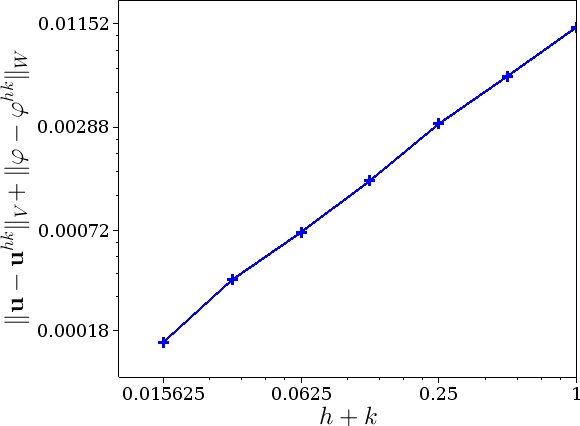
To see the convergence behaviour of the fully discrete scheme, we compute a sequence of numerical solutions based on uniform partitions of the time interval \([0, T]\), and uniform triangulations of the body. Then, we provide the estimated error values for several discretization parameters \(h\) and \(k\). Here, the sides of the square are divided into \(1/h\) equal parts and the time interval \([0,T]\) is divided into \(1/k\) time steps. We start with \(h = 1/2\) and \(k = 1/2\) which are successively halved. The numerical solution corresponding to \(h = 1/256\) and \(k = 1/256\) is taken as the “exact” solution, which is used to compute the errors of the numerical solutions with larger values of \(h\) and \(k\); this finer discretization corresponds to a problem with around \( 199432 \) degrees of freedom. The linear asymptotic convergence behaviour obtained in (25) is almost observed (see Figure 4).

5. Conclusion

In this paper we have provided an error estimate of a mathematical model which describes the frictional contact between an electro-viscoelastic body and a conductive foundation. The numerical treatment of the frictional contact conditions is obtained by combining the penalty method for the normal compliance condition and the augmented Lagrangian approach for the friction condition. Moreover, numerical simulations for a representative two-dimensional example were provided. These simulations validate the theoretical error estimates and, in addition, allow to study the influence of the electric potential field of the foundation on the process. This work opens the way to study further problems with other conditions for thermally-electrically conductive taking into the account the frictional heating effects.

conflictofinterests

The author declares no conflict of interest.