Certain results on starlike and convex functions

1. Introduction

Let \(\mathcal{T}(p)\) denote the class of functions \(f\) of the form

\[f(z)= z^{p}+\displaystyle\sum_{k=p+1}^{\infty} a_{k}z^{k},~\text{ where}~p\in\mathbb{N}=\{1,~2,~3,~\dots\},\] which are analytic and \(p-\)valent in the open unit disk \(\mathbb{E} = \{z\in\mathbb{C}:|z|\alpha,~~~~(0\leq\alpha < p;~z\in \mathbb{E}).\]

On the other hand, a function \(f\in \mathcal{T}(p)\) is said to be in the class \(\mathcal{K}_{p}(\alpha)\) of \(p-\)valently convex functions of order \(\alpha\) in \(\mathbb{E},\) if and only if it satisfies \[\Re\left(1+\dfrac{zf”(z)}{f'(z)}\right)>\alpha,~~~~(z\in\mathbb{E};~0\leq\alpha < p).\]

In particular, we write \(\mathcal{S}^{*}_{1}(0)=\mathcal{S}^{*}\) and \(\mathcal{K}_{1}(0)=\mathcal{K},\) where \(\mathcal{S}^{*}\) and \(\mathcal{K}\) are the usual subclasses of \(\mathcal{T} (=\mathcal{T}(1))\) consisting of functions which are starlike and convex respectively. Write \(\mathcal{S}^{*}_{p}(0)=\mathcal{S}^{*}_{p}\) and \(\mathcal{K}_{p}(0)=\mathcal{K}_{p}.\)

Let \(\Phi : \mathbb C^{2}\times \mathbb E \rightarrow \mathbb C\) be an analytic function, \(p\) be an analytic function in \(\mathbb E\) with \((p(z),zp'(z);z)\in \mathbb C^{2}\times \mathbb E\) for all \(z\in \mathbb E\) and \(h\) be univalent in \(\mathbb E.\) Then the function \(p\) is said to satisfy first order differential subordination if

A univalent function \(q\) is called a dominant of the differential subordination (1) if \(p(0) = q(0) \text{ and}~p\prec q\) for all \(p\) satisfying (1). A dominant \(\tilde {q}\) that satisfies \(\tilde{q}\prec q\) for all dominants \(q\) of (1), is said to be the best dominant of (1).

In 2003, Irmak et al. [1] introduced and studied the subclass \(\mathcal{T}_{\lambda}(p;~\alpha)\) of \(\mathcal{T}(p).\) According to them a function \(f\in\mathcal{T}(p)\) is said to be in \(\mathcal{T}_{\lambda}(p;~\alpha)\) if it satisfies the inequality

\begin{equation*} \Re\left\{\dfrac{zf'(z)+\lambda z^{2}f”(z)}{(1-\lambda)f(z)+\lambda z f'(z)}\right\}>\alpha \end{equation*} for \(z\in\mathbb{E};~0\leq\lambda\leq 1;~0\leq\alpha< p;~p\in\mathbb{N}.\) The following subclasses are the particular cases of class \(\mathcal{T}_{\lambda}(p;~\alpha):\) \begin{eqnarray*} \mathcal{T}_{\lambda}(1;~\alpha)&=& \mathcal{T}_{\lambda}(\alpha),~~~~0\leq\lambda\leq 1;~0\leq\alpha < 1,\\ \mathcal{T}_{0}(p;~\alpha)&=& \mathcal{S}^{*}_{p}(\alpha),~~~~0\leq\alpha< p;~p\in\mathbb{N},\\ \mathcal{T}_{1}(p;~\alpha)&=& \mathcal{K}_{p}(\alpha),~~~~0\leq\alpha< p;~p\in\mathbb{N},\\ \mathcal{T}_{0}(\alpha)&=& \mathcal{S}^{*}_{1}(\alpha)\subseteq\mathcal{S}^{*}(\alpha)\subseteq \mathcal{S}^{*}(0)=\mathcal{S}^{*},~~~0\leq\alpha< 1,\\ \mathcal{T}_{1}(\alpha)&=& \mathcal{K}_{1}(\alpha)\subseteq\mathcal{K}(\alpha)\subseteq \mathcal{K}(0)=\mathcal{K},~~~0\leq\alpha < 1. \end{eqnarray*}

Irmak et al. [1] obtained general results for \(f\in\mathcal{T}_{\lambda}(p;~\alpha)\) which combined certain types of inequalities concerning functions belonging to the classes \(\mathcal{S}^{*}_{p}(\alpha),~\mathcal{K}_{p}(\alpha),\) \(\mathcal{S}^{*}_{p},~\mathcal{K}_{p},~\mathcal{S}^{*}(\alpha),~\mathcal{K}(\alpha),~\mathcal{S}^{*}\) and \(\mathcal{K}.\) They obtained the following result:

Theorem 1. Let \(z\in \mathbb{E},~0\leq \alpha< p,~p\in\mathbb{N}\) and let a function \(f\in\mathcal{T}(p).\) Define a function \(F(z)\) by \[F(z)=(1-\lambda)f(z)+\lambda zf'(z),~~0\leq\lambda\leq 1,\] and if \(F\) satisfies anyone of the following inequalities:

\begin{eqnarray}\label{req1} \left|\dfrac{1+\dfrac{zF”(z)}{F'(z)}-p}{\dfrac{zF'(z)}{F(z)}-p}-1\right|&<& \dfrac{1}{2p-\alpha},\\ \end{eqnarray}

(2)

\begin{eqnarray}\label{req2} \left|1+z\left(\dfrac{F”(z)}{F'(z)}-\dfrac{F'(z)}{F(z)}\right)\right|&<& \dfrac{p-\alpha}{2p-\alpha},\\ \end{eqnarray}

(3)

\begin{eqnarray}\label{req3} \left|\dfrac{F(z)}{zF'(z)}\left(1+\dfrac{zF”(z)}{F'(z)}\right)-1\right|&<& \dfrac{p-\alpha}{(2p-\alpha)^{2}},\\ \end{eqnarray}

(4)

\begin{eqnarray}\label{req4} \left|\dfrac{zF'(z)}{F(z)}\left[1+z\left(\dfrac{F”(z)}{F'(z)}-\dfrac{F'(z)}{F(z)}\right)\right]\right|&<& p-\alpha,\\ \end{eqnarray}

(5)

\begin{eqnarray}\label{req5} \Re\left\{\dfrac{zF'(z)}{F(z)}\left(\dfrac{1+\dfrac{zF”(z)}{F'(z)}-p}{\dfrac{zF'(z)}{F(z)}-p}-1\right)\right\}&<& 1, \end{eqnarray}

(6)

then \(f\in\mathcal{T}_{\lambda}(p;~\alpha).\)

Irmak et al. [2,3,4] also provided interesting results for starlikeness and convexity of multivalent functions involving certain inequalities.

The objective of present paper is to study the class \(\mathcal{T}_{\lambda}(p;~\alpha)\) using the technique of differential subordination to conclude the similar results. We notice that in this practice the region of variability of operators studied has been extended considerably.

2. Preliminary

We shall need the following lemma to prove our main results.

Lemma 1. [5,Theorem 3.4h,p.132]. Let q be univalent in \(\mathbb{E}\) and let \(\theta\) and \(\phi\) be analytic in a domain \(\mathbb{D}\) containing \(q(\mathbb{E}),\) with \(\phi(w)\neq 0,\) when \(w\in q(\mathbb{E}).\) Set \(Q(z)=zq'(z)\phi[q(z)],~h(z) = \theta[q(z)]+Q(z)\) and suppose that either

• (i) h is convex, or
• (ii) \(Q\) is starlike.

In addition, assume that

• (iii) \(\Re \left(\displaystyle\frac{zh'(z)}{Q(z)}\right)>0.\)

If \(p\) is analytic in \(\mathbb{E},\) with \(p(0)= q(0), ~p(\mathbb{E})\subset \mathbb{D}\) and \[\theta[p(z)]+zp'(z)\phi[p(z)]\prec \theta[q(z)]+zq'(z)\phi[q(z)],\] then \(p\prec q,\) and \(q\) is the best dominant.

3. Main Results

Theorem 2. Let \(q\) be a univalent function in \(\mathbb{E}\) with \(q(z)\neq \{0,~m\},~m\in\mathbb{N}_{0}=\mathbb{N}\cup\{0\}\) and \[\Re \left(1+\dfrac{zq”(z)}{q'(z)}-\beta\dfrac{zq'(z)}{q(z)}-\gamma\dfrac{zq'(z)}{q(z)-m}\right)>0,~z\in \mathbb{E}.\] Suppose that \(f\in \mathcal{T}(p).\) Define a function \(F(z)\) as \[F(z)=(1-\lambda)f(z)+\lambda zf'(z),~0\leq \lambda\leq 1,\] and if \(F\) is such that \(\dfrac{zF'(z)}{F(z)}\neq \{0,~m\}\) and satisfies

where the complex powers in (7) take their principal values, then \[\dfrac{zF'(z)}{F(z)}\prec q(z),~z\in \mathbb{E},\] and \(q\) is the best dominant.

Proof. For \(f\in\mathcal{T}(p)\) and \(F(z)=(1-\lambda)f(z)+\lambda zf'(z),\) we have \[\frac{zF'(z)}{F(z)}=\dfrac{zf'(z)+\lambda z^{2}f”(z)}{(1-\lambda)f(z)+\lambda zf'(z)}.\] Let \(u(z)=\dfrac{zF'(z)}{F(z)}.\) Therefore (7) reduces to \[1+\dfrac{zu'(z)}{u^{\beta}(z)(u(z)-m)^{\gamma}}\prec 1+\dfrac{zq'(z)}{q^{\beta}(z)(q(z)-m)^{\gamma}}.\] Define \(\theta\) and \(\phi\) as \[\theta(w) = 1~\text{and}~\phi(w)=\frac{1}{w^{\beta}(w-m)^{\gamma}}\] where \(\theta\) and \(\phi\) are analytic in \(\mathbb{C}\setminus\{0,~m\}\) and \(\phi(w)\neq 0,~w\in\mathbb{C}\setminus\{0,~m\}.\) Therefore \[Q(z)=zq'(z)\phi(q(z))=\dfrac{zq'(z)}{q^{\beta}(z)(q(z)-m)^{\gamma}}\] and \(h(z)=\theta(q(z))+Q(z)=1+Q(z).\) A little calculation yields \[\frac{zQ'(z)}{Q(z)}=1+\frac{zq”(z)}{q'(z)}-\beta\frac{zq'(z)}{q(z)}-\gamma\frac{zq'(z)}{q(z)-m}\]and \[\frac{zh'(z)}{Q(z)}=\frac{zQ'(z)}{Q(z)} .\] In view of the given condition, we have \(Q(z)\) is starlike in \(\mathbb{E}\) and \[\Re\left(\dfrac{zh'(z)}{Q(z)}\right)>0.\] The proof, now, follows from Lemma 1.

For \(\beta=1=\gamma\) and \(m=p,\) Theorem 2 reduces to the following result:

Theorem 3. Let \(q\) be a univalent function in \(\mathbb{E},\) with \(q(z)\neq \{0,~p\},~p\in\mathbb{N}\) and satisfying the following condition\[\Re\left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)}-\dfrac{zq'(z)}{q(z)-p}\right)>0.\] Suppose that \(f\in \mathcal{T}(p)\) and define \(F(z)=(1-\lambda)f(z)+\lambda z f'(z),~~0\leq\lambda\leq 1.\) If \(F,~\dfrac{zF'(z)}{F(z)}\neq\{0,~p\},\) satisfies the differential subordination \begin{equation*} \dfrac{1+\dfrac{zF”(z)}{F'(z)}-p}{\dfrac{zF'(z)}{F(z)}-p}\prec 1+\dfrac{zq'(z)}{q(z)(q(z)-p)}, \end{equation*} then \[\dfrac{zF'(z)}{F(z)}\prec q(z),~z\in \mathbb{E},\] and \(q\) is the best dominant.

Proof. Proof of this theorem is on the similar lines as that of the proof of Theorem 2 for \(\beta=1=\gamma\) and \(m=p.\)

On selecting \(q(z)=1+\dfrac{2}{3}z^{2}\) as a dominant in the above result, we observe that for a natural number \(p,~ p\geq 2,\)

\[\Re \left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)}-\dfrac{zq'(z)}{q(z)-p}\right)=\Re \left(\dfrac{18(1-p)-8z^{4}}{9(1-p)+6z^{2}(2-p)+4z^{4}}\right)>0.\] Thus, we have the following result:

Corollary 1. For natural number \(p,~p\geq 2~and~0\leq\lambda\leq 1,\) let \(f\in \mathcal{T}(p)\) and define \(F(z)=(1-\lambda)f(z)+\lambda z f'(z).\) If \(F,~\dfrac{zF'(z)}{F(z)}\neq\{0,~p\},\) satisfies the condition \begin{equation*} \dfrac{1+\dfrac{zF”(z)}{F'(z)}-p}{\dfrac{zF'(z)}{F(z)}-p}\prec 1+\dfrac{12z^{2}}{(3+2z^{2})(3+2z^{2}-3p)}, \end{equation*} then \[\dfrac{zF'(z)}{F(z)}\prec 1+\dfrac{2}{3}z^{2},~z\in \mathbb{E},\] hence \(f\in \mathcal{T}_{\lambda}(p;~0). \)

We have the following observations:

Remark 1.

• (i) On taking \(\lambda=0\) in Corollary 1, we have: If \(f\in \mathcal{T}(p),~\dfrac{zf'(z)}{f(z)}\neq \{0,~p\},\) where \(p\in\mathbb{N}~{\text and}~ p\geq 2,\) satisfies \begin{equation*} \dfrac{1+\dfrac{zf”(z)}{f'(z)}-p}{\dfrac{zf'(z)}{f(z)}-p}\prec 1+\dfrac{12z^{2}}{(3+2z^{2})(3+2z^{2}-3p)}, \end{equation*} then \[\dfrac{zf'(z)}{f(z)}\prec 1+\dfrac{2}{3}z^{2},~z\in\mathbb{E},\] and hence \(f\in\mathcal{S}^{*}_{p}.\)
• (ii) For \(p=2\) in the above result, we have: If \(f\in\mathcal{T}(2),~\dfrac{zf'(z)}{f(z)}\neq \{0,~2\},\) satisfies
  \begin{equation} \label{ircomp11} \dfrac{f(z)}{zf'(z)-2f(z)}\left(\dfrac{zf”(z)}{f'(z)}-1\right)\prec 1+\dfrac{12z^{2}}{4z^{4}-9},~~z\in\mathbb{E}. \end{equation}

  (8)
  then \[\dfrac{zf'(z)}{f(z)}\prec 1+\dfrac{2}{3}z^{2},\] hence \(f\in\mathcal{S}^{*}_{2}.\) Putting \(\alpha=0=\lambda\) and \(p=2\) in (2) of Theorem 1, we get: If \(f\in\mathcal{T}(2),~\dfrac{zf'(z)}{f(z)}\neq \{0,~2\},\) satisfies
  \begin{equation} \label{ircomp12} \left| \dfrac{f(z)}{zf'(z)-2f(z)}\left(\dfrac{zf”(z)}{f'(z)}-1\right)-1\right|< \dfrac{1}{4},~~z\in\mathbb{E}. \end{equation}

  (9)
  then \(f\in\mathcal{S}^{*}_{2}.\)
• (iii) By selecting \(\lambda=1\) in Corollary 1, we get the following result:

  If \(f\in \mathcal{T}(p),~1+\dfrac{zf”(z)}{f'(z)}\neq \{0,~p\},\) where \(p\in\mathbb{N}~{\text and}~ p\geq 2,\) satisfies

  \begin{equation*} \dfrac{1+\dfrac{z(2f”(z)+zf”'(z))}{f'(z)+zf”(z)}-p}{1+\dfrac{zf”(z)}{f'(z)}-p}\prec 1+\dfrac{12z^{2}}{(3+2z^{2})(3+2z^{2}-3p)}, \end{equation*} then \[1+\dfrac{zf”(z)}{f'(z)}\prec 1+\dfrac{2}{3}z^{2},~z\in\mathbb{E},\] thus \(f\in\mathcal{K}_{p}.\)
• (iv) On taking \(p=2\) in the above result, we have:

  If \(f\in\mathcal{T}(2),~\dfrac{zf”(z)}{f'(z)}\neq 1,\) satisfies

  \begin{equation} \label{ircomp13} \dfrac{f'(z)\left(f'(z)-zf”(z)-z^{2}f”'(z)\right)}{f’^{2}(z)-z^{2}f”^{2}(z)}\prec 1+\dfrac{12z^{2}}{4z^{4}-9}, \end{equation}

  (10)
  then \[1+\dfrac{zf”(z)}{f'(z)}\prec 1+\dfrac{2}{3}z^{2},~z\in\mathbb{E},\] hence \(f\in\mathcal{K}_{2}.\)

  For \(\lambda=1\) and on selecting \(\alpha=0,~p=2\) in (2) of Theorem 1, we obtain:

  If \(f\in\mathcal{T}(2),~\dfrac{zf”(z)}{f'(z)}\neq 1,\) satisfies

  \begin{equation} \label{ircomp14} \left|\dfrac{f'(z)\left(f'(z)-zf”(z)-z^{2}f”'(z)\right)}{f’^{2}(z)-z^{2}f”^{2}(z)}-1\right|< \frac{1}{4} ,\end{equation}

  (11)
  then \(f\in\mathcal{K}_{2},~z\in\mathbb{E}.\)

We observe that according to (8), the operator \(\dfrac{f(z)}{zf'(z)-2f(z)}\left(\dfrac{zf”(z)}{f'(z)}-1\right)\) maps the open unit disk over the total shaded region shown in Figure 1, whereas according to (9), same operator takes values in the disk of radius 1/4 centered at \((1, 0)\) to conclude that \(f\in\mathcal{S}^{*}_{2}.\) Thus the result in (8) gives an extension of region over the region given by (9) for the same conclusion. In view of (10), the operator \(\dfrac{f'(z)\left(f'(z)-zf”(z)-z^{2}f”'(z)\right)}{f’^{2}(z)-z^{2}f”^{2}(z)}\) varies in the total shaded region shown in Figure 1, while it takes values in disk of radius 1/4 centered at \((1, 0)\) according to (11). Thus the region of variation extends in (10) over (11) for the operator \(\dfrac{f'(z)\left(f'(z)-zf”(z)-z^{2}f”'(z)\right)}{f’^{2}(z)-z^{2}f”^{2}(z)}\) to conclude that \(f\in\mathcal{K}_{2}.\)

By taking \(\beta = 1\) and \(\gamma=0\) in Theorem 2, we have the following result:

Theorem 4. Let \(q\) be a univalent function in \(\mathbb{E},\) with \(q\) satisfy \[\Re \left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)}\right)>0.\] Suppose that \(f\in \mathcal{T}(p),~p\in\mathbb{N}\) and define \(F(z)=(1-\lambda)f(z)+\lambda z f'(z),\) where \(0\leq\lambda\leq 1.\) If \(F,~\dfrac{zF'(z)}{F(z)}\neq 0,\) satisfies \begin{equation*} 1+\dfrac{zF”(z)}{F'(z)}-\dfrac{zF'(z)}{F(z)}\prec \dfrac{zq'(z)}{q(z)},~z\in \mathbb{E}, \end{equation*} then \[\dfrac{zF'(z)}{F(z)}\prec q(z),\] and \(q\) is the best dominant.

Proof. The proof can be obtained by taking \(\beta=1,~\gamma=0\) in the proof of Theorem 2.

Selecting \(q(z)=\dfrac{1+z}{1-z}\) as a dominant in the above theorem, we can easily check that

\[\Re \left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)}\right)=\Re \left(\dfrac{1+z^2}{1-z^2}\right)>0.\] Hence we have the following result:

Corollary 2. Let \(f\in \mathcal{T}(p),~p\in\mathbb{N}\) and \(F(z)=(1-\lambda)f(z)+\lambda z f'(z)\) such that \(\dfrac{zF'(z)}{F(z)}\neq 0.\) If \(F\) satisfies \[1+\dfrac{zF”(z)}{F'(z)}-\dfrac{zF'(z)}{F(z)}\prec \dfrac{2z}{1-z^{2}},\] then \[\dfrac{zF'(z)}{F(z)}\prec \dfrac{1+z}{1-z},~z\in \mathbb{E},\] hence \(f\in\mathcal{T}_{\lambda}(p;~0).\)

We have the following observations regarding the above result:

Remark 2.

• (i) On taking \(\lambda=0,\) in Corollary 2, we have:

  If \(f\in \mathcal{T}(p),~\dfrac{zf'(z)}{f(z)}\neq 0, \text{ where}~p\in\mathbb{N}\) satisfies the following \begin{equation*} 1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\prec \dfrac{2z}{1-z^{2}},\end{equation*} then \[\dfrac{zf'(z)}{f(z)}\prec \dfrac{1+z}{1-z},~~ z\in\mathbb{E},\] and hence \(f\) is \(p-\)valently starlike.

• (ii) By putting \(p=1,\) in the above result, we conclude that:

  If \( f\in \mathcal{T},~\dfrac{zf'(z)}{f(z)}\neq 0,\) satisfies the differential subordination

  \begin{equation} \label{ircomp21} 1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)} \prec \dfrac{2z}{1-z^{2}},\end{equation}

  (12)
  then \[\dfrac{zf'(z)}{f(z)}\prec \dfrac{1+z}{1-z},~~ z\in\mathbb{E},\] and hence we conclude that \(f\) is starlike.

  For \(\alpha=0=\lambda\) and \(p=1\), result can be obtained from (3) of Theorem 1, as below:

  If \( f\in \mathcal{T}\) satisfies
  \begin{equation} \label{ircomp22} \left|1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)} \right|< \frac{1}{2} \end{equation}

  (13)
  then \(f\in\mathcal{S}^{*}.\)
• (iv) Selecting \(\lambda=1\) in Corollary 2, we get:

  Let \(f\in\mathcal{T}(p),~p\in\mathbb{N}\) satisfies

  \begin{equation*} \dfrac{z(2f”(z)+zf”'(z))}{f'(z)+zf”(z)}-\dfrac{zf”(z)}{f'(z)}\prec \dfrac{2z}{1-z^{2}},~~z\in\mathbb{E} \end{equation*} then \[1+\dfrac{zf”(z)}{f'(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\in\mathcal{K}_{p}.\),
• (v) For \(p=1\) in the above result, we get:

  Let \(f\in\mathcal{T}\) satisfies

  \begin{equation} \label{ircomp23} \dfrac{z(2f”(z)+zf”'(z))}{f'(z)+zf”(z)}-\dfrac{zf”(z)}{f'(z)}\prec \dfrac{2z}{1-z^{2}},~~z\in\mathbb{E} \end{equation}

  (14)
  then \[1+\dfrac{zf”(z)}{f'(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\) is convex.

  For \(p=1=\lambda\) and \(\alpha =0\) we get from (3) of Theorem 1:

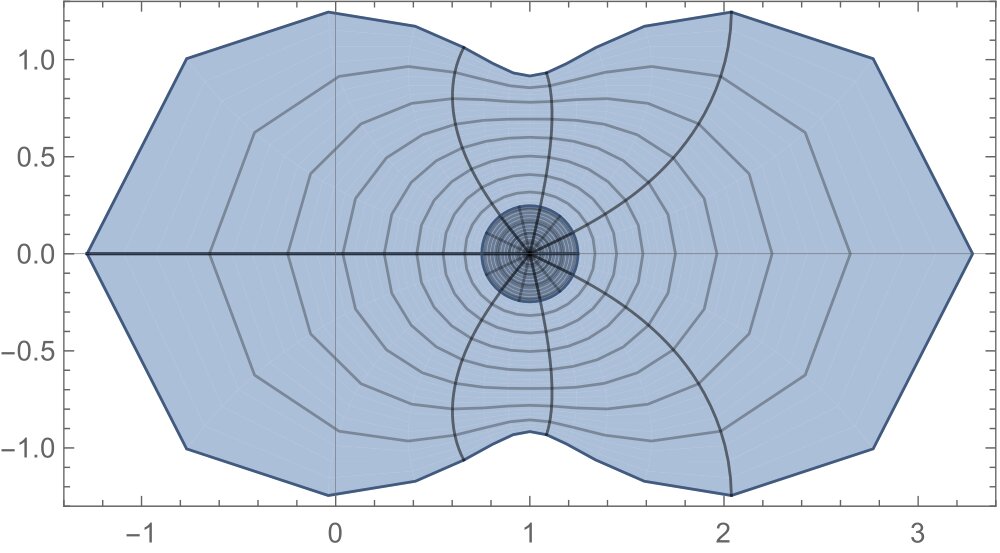
  Let \(f\in\mathcal{T}\) satisfies
  \begin{equation} \label{ircomp24} \left|\dfrac{z(2f”(z)+zf”'(z))}{f'(z)+zf”(z)}-\dfrac{zf”(z)}{f'(z)}\right|< \dfrac{1}{2},~~z\in\mathbb{E} \end{equation}

  (15)
  hence \(f\) is convex.

According to (12), \(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\) takes values in the whole complex plane except two slits along imaginary axis from \(-\infty\) to \(-1\) and from \(1\) to \(\infty\) to conclude that \(f\) is starlike. While this operator in view of (13) takes values in the disk of radius 1/2 with center at origin to conclude that \(f\) is starlike. The facts have been shown pictorially in Figure 2. Thus region of variation for the operator \(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\) extends in (12) over the region given in (13) for \(f\) to be starlike. Similarly the region of variation for \(\dfrac{z(2f”(z)+zf”'(z))}{f'(z)+zf”(z)}-\dfrac{zf”(z)}{f'(z)}\) extends in (14) over the region given in (15) for \(f\) to be convex.

Selecting \(\beta=\gamma=1\) and \(m=0\) in Theorem 2, we get the following result:

Theorem 5. Let \(q,~q\neq 0\) be a univalent function satisfying \[\Re\left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{2zq'(z)}{q(z)} \right)> 0,~z\in\mathbb{E}.\] Let \(f\in\mathcal{T}(p),~p\in\mathbb{N}~and~F(z)= (1-\lambda)f(z)+z\lambda f'(z),~0\leq\lambda\leq 1.\) If \(F,~\dfrac{zF'(z)}{F(z)}\neq 0,\) satisfies \begin{equation*} \dfrac{F(z)}{zF'(z)}\left(1+\dfrac{zF”(z)}{F'(z)}\right)\prec 1+\dfrac{zq'(z)}{q^{2}(z)},~z\in\mathbb{E}, \end{equation*} then \[\dfrac{zF'(z)}{F(z)}\prec q(z),\] and \(q\) is the best dominant.

Proof. For \(\beta=\gamma=1\) and \(m=0\) the proof of this theorem is on the similar lines as the proof of Theorem 2.

Choosing \(q(z)=\dfrac{1+z}{1-z}\) as a dominant in the above theorem, we can easily check that \(\Re\left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{2zq'(z)}{q(z)} \right)=\Re \left(\dfrac{1-z}{1+z}\right)> 0.\) Hence we get:

Corollary 3. Let \(f\in\mathcal{T}(p),~p\in\mathbb{N}.\) If \(F(z)= (1-\lambda)f(z)+z\lambda f'(z),~\dfrac{zF'(z)}{F(z)}\neq 0,~0\leq\lambda\leq 1,\) satisfies \begin{equation*} \dfrac{F(z)}{zF'(z)}\left(1+\dfrac{zF”(z)}{F'(z)}\right)\prec \dfrac{1+4z+z^{2}}{(1+z)^{2}},~z\in\mathbb{E}, \end{equation*} then \[\dfrac{zF'(z)}{F(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\in\mathcal{T}_{\lambda}(p;~0).\)

We have the following observations:

Remark 3.

• (i) For \(\lambda=0\) in Corollary 3, we get:

  If \(f\in\mathcal{T}(p),~\dfrac{zf'(z)}{f(z)}\neq 0,~p\in\mathbb{N}\) and satisfies

  \[\dfrac{f(z)}{zf'(z)}\left(1+\dfrac{zf”(z)}{f'(z)}\right)\prec \dfrac{1+4z+z^{2}}{(1+z)^{2}},~z\in\mathbb{E},\] then \[\dfrac{zf'(z)}{f(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\in\mathcal{S}^{*}_{p}.\)
• (ii) Putting \(p=1\) in the above result, we have:

  If \(f\in\mathcal{T},~\dfrac{zf'(z)}{f(z)}\neq 0,\) satisfies

  \begin{equation} \label{ircomp31}\dfrac{f(z)}{zf'(z)}\left(1+\dfrac{zf”(z)}{f'(z)}\right)\prec \dfrac{1+4z+z^{2}}{(1+z)^{2}},~z\in\mathbb{E}, \end{equation}

  (16)
  then \[\dfrac{zf'(z)}{f(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\in\mathcal{S}^{*}.\)

  For \(\lambda=0,~p=1\) and \(\alpha=0\) from (4) of Theorem 1, we get:

  If \(f\in\mathcal{T},~\dfrac{zf'(z)}{f(z)}\neq 0,\) satisfies
  \begin{equation} \label{ircomp32}\left|\dfrac{f(z)}{zf'(z)}\left(1+\dfrac{zf”(z)}{f'(z)}\right)-1\right|< \frac{1}{4}, ~z\in\mathbb{E}, \end{equation}

  (17)
  hence \(f\) is starlike.
• (iii) Putting \(\lambda=1\) in Corollary 3, we have:

  If \(f\in\mathcal{T}(p),~p\in\mathbb{N}\) satisfies the condition

  \[\dfrac{f'(z)(f'(z)+3zf”(z)+z^{2}f”'(z))}{(f'(z)+zf”(z))^{2}}\prec \dfrac{1+4z+z^{2}}{(1+z)^{2}},~z\in\mathbb{E},\] then \[1+\dfrac{zf”(z)}{f'(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\in\mathcal{K}_{p}.\)
• (iv) On substituting \(p=1\) in the above result, we get:

  Let \(f\in\mathcal{T}\) satisfies

  \begin{equation} \label{ircomp33} \dfrac{f'(z)(f'(z)+3zf”(z)+z^{2}f”'(z))}{(f'(z)+zf”(z))^{2}}\prec \dfrac{1+4z+z^{2}}{(1+z)^{2}},~z\in\mathbb{E}, \end{equation}

  (18)
  then \[1+\dfrac{zf”(z)}{f'(z)}\prec \dfrac{1+z}{1-z},\] hence \(f\in\mathcal{K}.\)

  For \(\lambda=1=p\) and \(\alpha=0\) in (4) of Theorem 1, we have the following result:

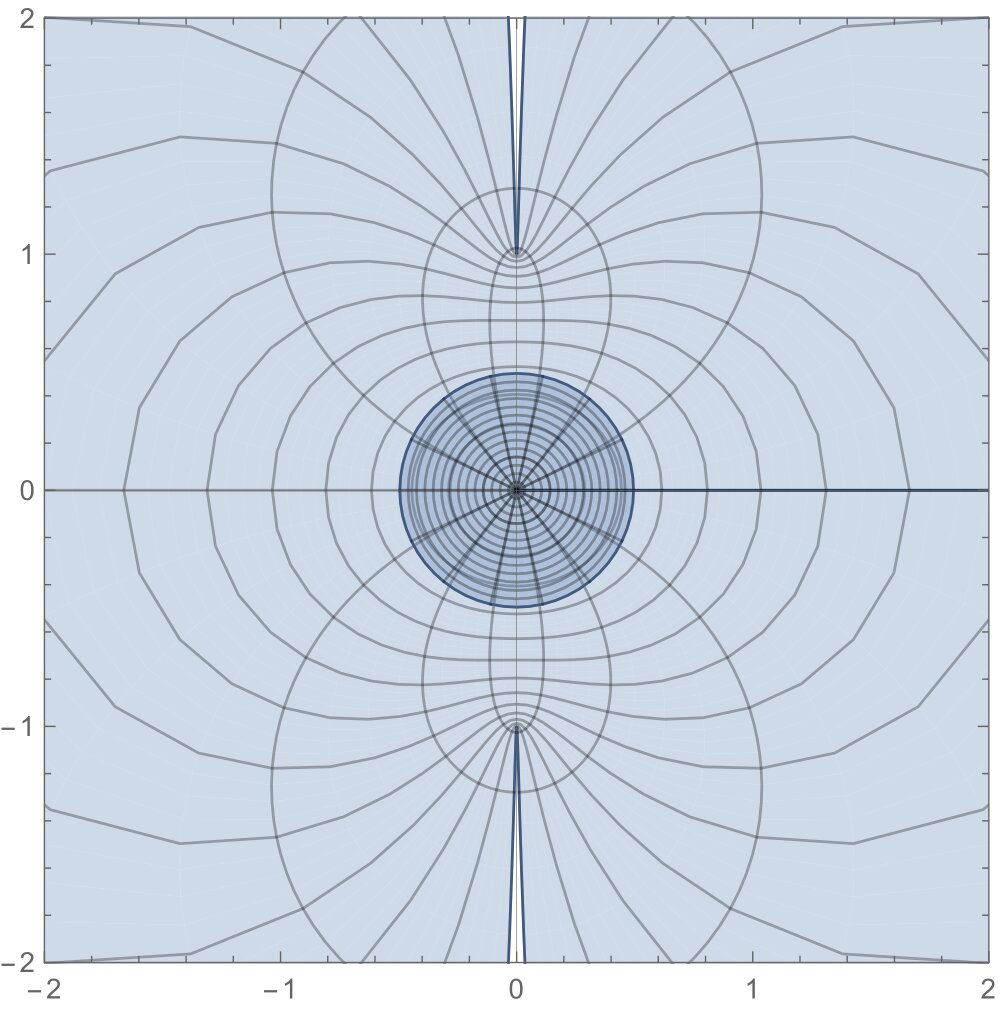
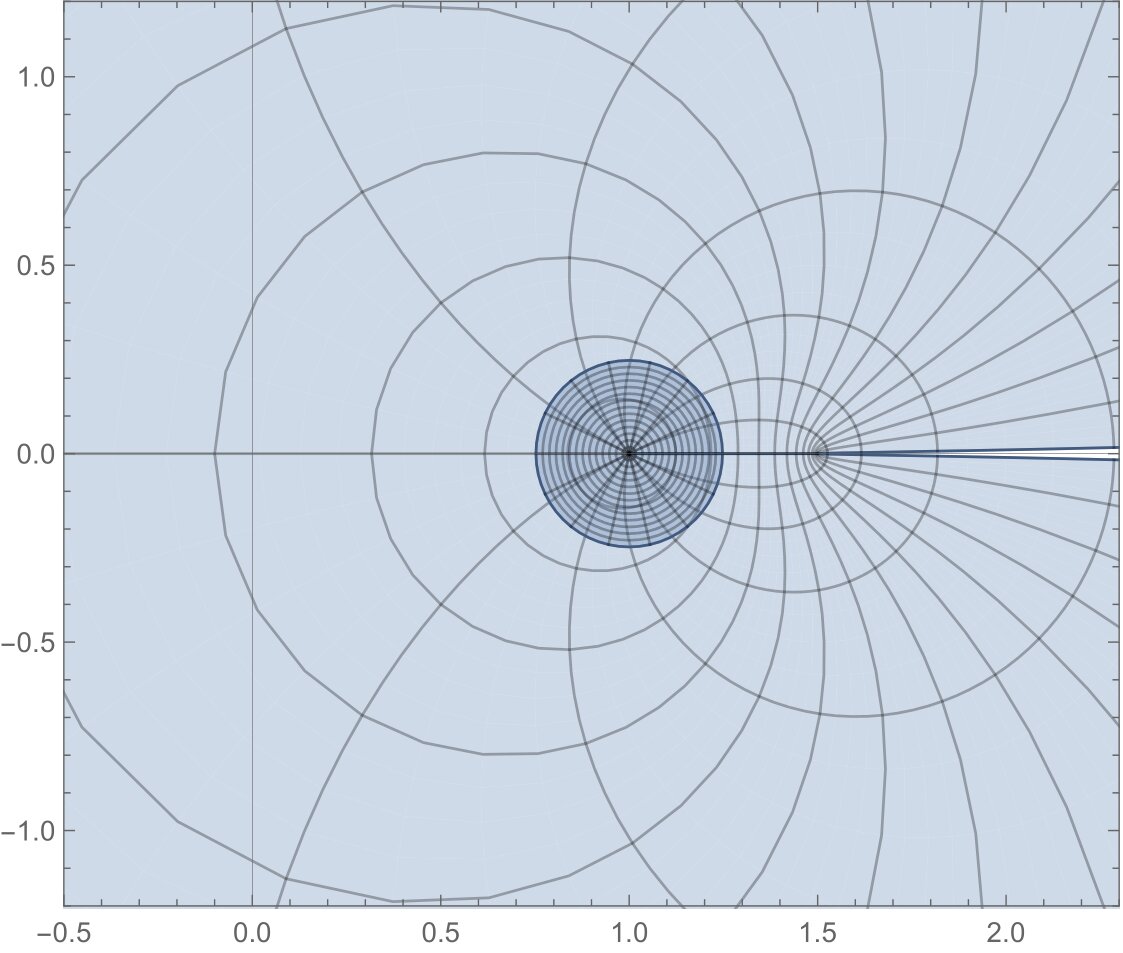
  If \(f\in\mathcal{T}\) satisfies
  \begin{equation} \label{ircomp34} \left|\dfrac{f'(z)(f'(z)+3zf”(z)+z^{2}f”'(z))}{(f'(z)+zf”(z))^{2}}-1\right|< \dfrac{1}{4},~z\in\mathbb{E}, \end{equation}

  (19)
  hence \(f\in\mathcal{K}.\)

  We observe in view of (16) that \(\dfrac{f(z)}{zf'(z)}\left(1+\dfrac{zf”(z)}{f'(z)}\right)\) takes values in the whole complex plane except the slit on real axis from \(3/2\) to \(\infty\) as shown in Figure 3 and according to (17), the same operator takes values in the disk of radius {1}/{4} centered at \((1, 0)\) to conclude that \(f\) is starlike. Therefore the region in (16) is an extension of the region given in (17) to conclude that \(f\in\mathcal{S}^{*}.\) Similarly, the region given in (18) for the operator \(\dfrac{f'(z)(f'(z)+3zf”(z)+z^{2}f”'(z))}{(f'(z)+zf”(z))^{2}}\) extends over the region given in (19) to conclude that \(f\) is convex. The facts are shown pictorially in Figure 3.

  

  Selecting \(\beta=0=\gamma\) in Theorem 2, we have the following result:

  Theorem 6. Let \(q\) be a convex univalent function and let \(f\in\mathcal{T}(p),~p\in\mathbb{N}.\) Define \(F(z)=(1-\lambda)f(z)+\lambda zf'(z),~0\leq\lambda\leq 1\) and if \(F,~\dfrac{zF'(z)}{F(z)}\neq 0,\) satisfies \begin{equation*} \dfrac{zF'(z)}{F(z)}\left(1+\dfrac{zF”(z)}{F'(z)}-\dfrac{zF'(z)}{F(z)}\right)\prec zq'(z),~~z\in\mathbb{E} \end{equation*} then \[\dfrac{zF'(z)}{F(z)}\prec q(z),\] and \(q \) is the best dominant.

  Proof. Proof of this theorem is on the similar lines as that of Theorem 2 for \(\beta=0=\gamma.\)

  Taking \(q(z)=1+\dfrac{2}{3}z^{2}\) as a dominant in the above theorem. We can easily check that \(\Re\left(1+\dfrac{zq”(z)}{q'(z)}\right)=\Re(2)>0.\) Hence, we get the following result:

  Corollary 4. Let \(f\in\mathcal{T}(p),~p\in\mathbb{N}.\) If \(F(z)= (1-\lambda)f(z)+z\lambda f'(z),~\dfrac{zF'(z)}{F(z)}\neq 0,~0\leq\lambda\leq 1,\) satisfies \[\dfrac{zF'(z)}{F(z)}\left(1+\dfrac{zF”(z)}{F'(z)}-\dfrac{zF'(z)}{F(z)}\right)\prec \dfrac{4}{3}z^{2},~z\in\mathbb{E}, \] then \[\dfrac{zF'(z)}{F(z)}\prec 1+\dfrac{2}{3}z^{2},\] hence \(f\in\mathcal{T}_{\lambda}(p;~0).\)

  We have the following observations regarding the above result:

  Remark 4.

  • (i) For \(\lambda=0\) in Corollary 4, we get:

    For \(f\in\mathcal{T}(p),\dfrac{zf'(z)}{f(z)}\neq 0,~p\in\mathbb{N},\) if \(f\) satisfies

    \[\dfrac{zf'(z)}{f(z)}\left(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\right)\prec \dfrac{4}{3}z^{2},~z\in\mathbb{E},\] then \[\dfrac{zf'(z)}{f(z)}\prec 1+\dfrac{2}{3}z^{2},\] hence \(f\in\mathcal{S}^{*}_{p}.\)
  • (ii) For \(p=1\) in the above result, we have :

    If \(f\in\mathcal{T},\dfrac{zf'(z)}{f(z)}\neq 0,\) satisfies

    \begin{equation} \label{ircomp41} \dfrac{zf'(z)}{f(z)}\left(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\right)\prec \dfrac{4}{3}z^{2},~ z\in\mathbb{E},\end{equation}

    (20)
    then \[\dfrac{zf'(z)}{f(z)}\prec 1+\dfrac{2}{3}z^{2},\] hence \(f\) is starlike.

    Putting \(\lambda=0,~p=1\) and \(\alpha=0\) in (5) of Theorem 1, we have:

    If \(f\in\mathcal{T},\) satisfies
    \begin{equation} \label{ircomp42} \left|\dfrac{zf'(z)}{f(z)}\left(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\right)\right|< 1,~ z\in\mathbb{E},\end{equation}

    (21)
    hence \(f\) is starlike.
  • (iii) Putting \(\lambda=1\) in Corollary 4, we have:

    Let \(f\in\mathcal{T}(p),~\dfrac{zf'(z)}{f(z)}\neq 0,~p\in\mathbb{N}.\) If \(f\) satisfies

    \[z\left(1+\dfrac{zf”(z)}{f'(z)}\right)\left(\dfrac{2f”(z)+zf”'(z)}{f'(z)+zf”(z)}-\dfrac{f”(z)}{f'(z)}\right)\prec \dfrac{4}{3}z^{2},\] then \[1+\dfrac{zf”(z)}{f'(z)}\prec 1+\dfrac{2}{3}z^{2},~z\in\mathbb{E},\] and hence \(f\) is \(p-\)valently convex.
  • (iv) For \(p=1\) in the above result, we get:

    If \(f\in\mathcal{T}\) satisfies

    \begin{equation} \label{ircomp43}z\left(1+\dfrac{zf”(z)}{f'(z)}\right)\left(\dfrac{2f”(z)+zf”'(z)}{f'(z)+zf”(z)}-\dfrac{f”(z)}{f'(z)}\right)\prec \dfrac{4}{3}z^{2}, \end{equation}

    (22)
    then \[1+\dfrac{zf”(z)}{f'(z)}\prec 1+\dfrac{2}{3}z^{2},~z\in\mathbb{E},\] and hence \(f\) is convex.

    On substituting \(p=1=\lambda\) and \(\alpha=0\) in (5) of Theorem 1, we obtain the following result:

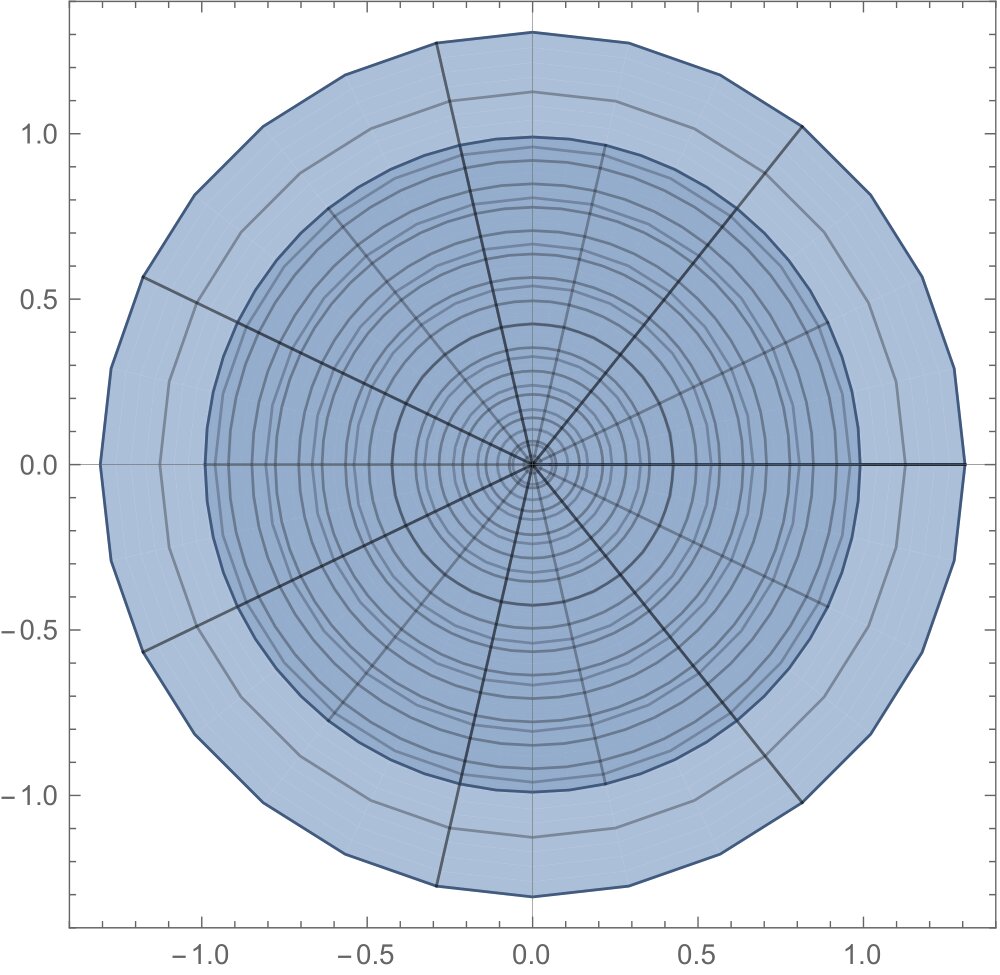
    If \(f\in\mathcal{T}\) satisfies
    \begin{equation} \label{ircomp44} \left|z\left(1+\dfrac{zf”(z)}{f'(z)}\right)\left(\dfrac{2f”(z)+zf”'(z)}{f'(z)+zf”(z)}-\dfrac{f”(z)}{f'(z)}\right)\right|< 1,~z\in\mathbb{E}, \end{equation}

    (23)
    then \(f\) is convex.

  In view of (20), we notice that the operator \(\dfrac{zf'(z)}{f(z)}\left(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\right)\) maps the open unit disk to the disk of radius 4/3 centered at origin to conclude that \(f\) is starlike while this operator in view of (21) takes values in unit disk, as shown in Figure 4, to conclude that \(f\) is starlike. Thus there is an extension of the region in (20) over (21) for the same conclusion. Similarly, there is an extension of the region in (22) over (23) for the operator \(z\left(1+\dfrac{zf”(z)}{f'(z)}\right)\left(\dfrac{2f”(z)+zf”'(z)}{f'(z)+zf”(z)}-\dfrac{f”(z)}{f'(z)}\right)\) to conclude that \(f\) is convex.

  

  Letting \(\beta=0,~\gamma=1\) and \(m=p\) in Theorem 2, we obtain the following result:

  Theorem 7. Let \(q\) be a univalent function with \(q(z)\neq p,~p\in\mathbb{N}\) and satisfy the condition \begin{equation*} \Re\left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)-p}\right)>0. \end{equation*} Let \(f\in\mathcal{T}(p),\) and define \(F(z)=(1-\lambda)f(z)+\lambda zf'(z),\) where \(0\leq\lambda\leq 1.\) If \(F,~\dfrac{zF'(z)}{F(z)}\neq \{0,~p\},\) satisfies \[ \dfrac{zF'(z)}{F(z)}\left(\dfrac{1+\dfrac{zF”(z)}{F'(z)}-\dfrac{zF'(z)}{F(z)}}{\dfrac{zF'(z)}{F(z)}-p}\right)\prec \dfrac{zq'(z)}{q(z)-p},~~z\in\mathbb{E}, \] then \[\dfrac{zF'(z)}{F(z)}\prec q(z),\] and \(q \) is the best dominant.

  Taking \(\lambda=0\) in above Theorem 7, we have:

  Corollary 5. Let \(q\) be a univalent function in \(\mathbb{E}\) with \(q(z)\neq ~p,~p\in\mathbb{N}\) and be such that \[ \Re\left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)-p}\right)>0.\] If \(f\in\mathcal{T}(p),~\dfrac{zf'(z)}{f(z)}\neq \{0,~p\},\) satisfies \[\dfrac{zf'(z)}{zf'(z)-pf(z)}\left(1+\dfrac{zf”(z)}{f'(z)}-\dfrac{zf'(z)}{f(z)}\right)\prec \dfrac{zq'(z)}{q(z)-p},~z\in\mathbb{E},\] then \[\dfrac{zf'(z)}{f(z)}\prec q(z),\] and \(q \) is the best dominant.

  Putting \(\lambda=1\) in Theorem 7, we have:

  Corollary 6. Let \(q\) be a univalent function in \(\mathbb{E}\) with \(q(z)\neq p,~p\in\mathbb{N}\) and be such that \[ \Re\left(1+\dfrac{zq”(z)}{q'(z)}-\dfrac{zq'(z)}{q(z)-p}\right)>0.\] Let \(f\in\mathcal{T}(p),~\dfrac{zf'(z)}{f(z)}\neq \{0,~p\},\) satisfy \[\left(1+\dfrac{zf”(z)}{f'(z)}\right)\left(\dfrac{f'(z)[2f”(z)+zf”'(z)]}{f”(z)[f'(z)+zf”(z)]}-1\right)\prec \dfrac{zq'(z)}{q(z)-p},~~z\in\mathbb{E},\] then \[1+\dfrac{zf”(z)}{f'(z)}\prec q(z),\] and \(q \) is the best dominant.

  acknowledgments

  The authors are thankful to the reviewer for valuable remarks.

  authorcontributions

  All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

  conflictofinterests

  The authors declare no conflict of interest.