In this investigation, we aim to investigate the novel exact solutions of nonlinear partial differential equations (NLPDEs) arising in electrical engineering via the -expansion method. New acquired solutions are kink, particular kink, bright, dark, periodic combined-dark bright and combined-dark singular solitons, and hyperbolic functions solutions. The achieved distinct types of solitons solutions contain critical applications in engineering and physics. Numerous novel structures (3D, contour, and density plots) are also designed by taking the appropriate values of involved parameters. These solutions express the wave show of the governing models, actually.
Current nonlinear science, mathematical physics, and engineering phenomena are associated with NLPDEs. These are much meaningful in describing everyday difficulties arising in nonlinear science and nature, such as computer science, waves, biology, geology, birefringent fibers, population ecology, fluid dynamics, solid-state physics, wave propagation, and many more. Numerous mathematical procedures have been efficiently implemented to investigate the important results of NLPDEs [1-23]. Utilizing these procedures, numerous new features of wave performance of these NLPDEs have been found. The results have much influence on diverse experimental phenomena such as long-distance high-speed transmission lines, optics, and optics as temporal or spatial optical solitons and optical fibers.
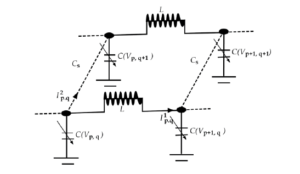
The purpose of this paper is to give the \((\Psi – \Phi)\)-expansion method [24] and the Hamiltonian system [25,26] to determine ESs for a discrete non-linear transmission line model [27-29]. The proposed equation is also known via the MZK model that assistances in defining the device of various characteristics [30-33] and describes the evolution of weakly non-linear ion-acoustic waves in a plasma involving hot iso-thermal electrons and cold-ions in the existence of a uniform-magnetic field in the x-direction. NLPDEs have been deliberate as essential in numerous applications. The proposed equation has been implemented to define natural, mechanical, multiple physical phenomena, and engineering. That performs because it contains beforehand unknown multi-variable tasks and their derivatives, such as the electrical transmission lines, which are proposed as a good standard of systems for examining non-linear excitations, behave inside non-linear media, as nominated in Figure 1.
The nonlinear electrical transmission line is proposed based on periodically loading with var-actors or organizing inductors and var-actors in a 1D lattice. The nonlinear network with some couple nonlinear LC with a dispersive transmission line has consisted of this equation. Numerous identical dispersive lines are coupled with capacitance \(C_{s}\) at each node, as denoted in Figure 1, where a conductor \(L\) and a nonlinear capacitor of capacitance \(C\left( v_{p,q} \right)\) are in each line in the shunt branch. The scientific equation which denotes the discrete nonlinear transmission is given via the MZK equation that is defined through Duan when he applied the Kirchhoff law on the equation, which as \[\label{1.1} \frac{\partial^{2}R_{p,q}}{{\partial S}^{2}} = \frac{1}{L}\left( V_{p + 1,q} – {2V}_{p,q} + V_{p – 1,q} \right) + C_{s}\frac{\partial^{2}}{{\partial S}^{2}}\left( V_{p,q + 1} – {2V}_{p,q} + V_{p,q – 1} \right),\tag{1}\] where \(V_{p,q} = V_{p,q}\left( S \right)\) is the voltage so that the non-linear charge is find as \[\label{1.2} R_{p,q} = C_{0}\left( V_{p,q} + \frac{\alpha_{1}}{2_{}}{V^{2}}_{p,q} + \frac{\alpha_{2}}{3_{}}{V^{3}}_{p,q} \right),\tag{2}\] where \(\alpha_{1}\),\(\alpha_{2}\) are arbitrary constants. Substituting Eq. (2) into Eq. (1), we have
\[\label{1.3} C_{0}\frac{\partial^{2}}{{\partial S}_{}^{2}}\left( V_{p,q} + \frac{\alpha_{1}}{2_{}}{V^{2}}_{p,q} + \frac{\alpha_{2}}{3_{}}{V^{3}}_{p,q} \right) = \frac{1}{L}\left( V_{p + 1,q} – {2V}_{p,q} + V_{p + 1,q} \right)+ C_{s}\frac{\partial^{2}}{{\partial S}^{2}}\left( V_{p,q + 1} – {2V}_{p,q} + V_{p,q – 1} \right)\,.\tag{3}\] Replacing \(V_{p,q}\left( S \right) = V\left( p,q,S \right)\), leads to \[\label{1.4} C_{0}\frac{\partial^{2}}{{\partial S}^{2}}\left( V + \frac{\alpha_{1}}{2_{}}V^{2} + \frac{\alpha_{2}}{3_{}}V^{3} \right) = \frac{1}{L}\frac{\partial^{2}}{{\partial p}^{2}}\left( V + \frac{1}{\text{12}}\frac{\partial^{2}}{{\partial p}^{2}} \right) + C_{s}\frac{\partial^{4}}{{\partial S}^{2}{\partial q}^{2}}\left( V + \frac{1}{\text{12}}\frac{\partial^{2}V}{{\partial q}^{2}} \right)\,.\tag{4}\] Based on the reductive perturbation technique, Eq. (4) is reduced to the following model: \[\label{1.5} \varphi_{t} + f_{1}\varphi\varphi_{x} + q\varphi^{2}\varphi_{x} +d\varphi _{xxx} + g\varphi _{xyy} = 0,\tag{5}\] where \(y=\sqrt{\gamma}q\), \(x=\sqrt{\gamma}(p-\nu_{s}S)\), \(t=\sqrt{\gamma}S\), \(V(p,q,S)=\gamma\varphi(x,y,t)\), \(\nu_{s}^{2}=\frac{1}{LC_{0}}\), \(f_{1}=-\alpha_{1}\nu_{s}\), \(q=-\alpha_{2}\nu_{s}\), \(d=\frac{1}{24\alpha\alpha_{1}L\nu_{s}}\), \(g=\frac{\alpha_{1}}{288L^{2}\nu_{s}C_{0}^{2}}\).
Consider \[ P(\hbar,\ \hbar_{x},\hbar_{x\ x},\hbar_{t},\hbar_{t\ t},\hbar_{\text{xt}}\text{.},\text{.}\text{.}\text{.}\text{.}\text{.}) = 0,\tag{6}\] where \(P\) is a polynomial in \(\hbar\) as well as its derivatives.
Firstly, use the traveling variable: \[\label{2.2} \hbar = \hbar(x,\ t) = \hbar\ (\chi),\ \chi = p_{3}(x – \text{Vt}),\tag{7}\] where \(p_{3}\) and \(V\) are a constant to be determine later. Using (7) into (6), we get
\[\label{2.3} R(\hbar,\ p_{3}\hbar^{'},p_{3}^{2}\hbar^{''}, – p_{3}V\hbar^{'},p_{3}^{2}V^{2}\hbar^{''}, – p_{3}^{2}V^{2}\hbar^{''},\text{.}\text{.}\text{.}\text{.}\text{.}) = 0\text{.}\tag{8}\] Secondly, consider \[\label{2.4} \hbar(\chi) = \sum_{i = 0}^{M}{S_{i}\Psi^{i} + \sum_{i = 1}^{M}{T_{i}\Psi^{i – 1}\Phi,}}\tag{9}\] where \(\Psi = (\Theta^{'}/\Theta)\) and \(\Phi = (\Omega^{'}/\Omega)\text{.}\) Now \(\Theta = \Theta(\chi)\) and \(\Omega = \Omega(\chi)\) are represent as \[\begin{aligned} &\Theta^{'}(\chi) = – \Theta(\chi)\ \Omega(\chi),\\ &\Omega^{'}(\chi) = 1 – \ \Omega(\chi)^{2}, \end{aligned}\] where \(\Theta(\chi) = \pm \text{sec}h(\chi),\) \(\Omega(\chi) = \text{tanh}(\chi),\) \(\Theta(\chi) = \pm \text{csc}h(\chi),\) and \(\Omega(\chi) = \text{coth}(\chi)\text{.}\)
Thirdly, a polynomial in \(\Psi\)or \(\Phi\) accomplised plugging Eq. (9) into Eq. (8). Defining the constant values of the corresponding power of \(\Psi\)or \(\Phi\) yields a system of equations, which might be defined to make \(S_{i}\) and \(T_{i}\). After getting \(S_{i}\) and \(T_{i}\) in (9), the answers of the studied model complete the intention of the answers of the proposed model.
Since \(x,y,t\) are independent transformation variables. Employing \(\varphi = \varphi\left( x,y,t \right) = \varphi\left( \eta \right),\) where \(\eta = k_{1}x + k_{2}y + k_{3}t\) into Eq. (5), we have \[\label{3.1} 6k_{3}\varphi + 3f_{1}k_{1}\varphi^{2} + 2\text{qk}_{1}\varphi^{3} + 6k_{1}\left( \text{dk}_{1}^{2} + \text{gk}_{2}^{2} \right)\varphi^{\text{''}} = 0\text{.}\tag{10}\] According the studied technique which we discuss in §2, we find \[\label{3.2} \hbar(\chi) = S_{0}\Psi^{0} + S_{1}\Psi^{1} + T_{1}\Psi^{0}\Phi = S_{0} + \frac{T_{1}}{\Omega} – (S_{1} + T_{1})\ \Omega\,.\tag{11}\] Collecting the coefficient of \(\Psi\) and \(\Phi\) and solving the resulting system, we get
Cluster I: Substituting \(k_{2} = \pm \sqrt{\frac{- 24dqk_{1}^{2} + f_{1}^{2}}{24gq},}\) \(k_{3} = \frac{1}{6}\frac{f_{1}^{2}k_{1}}{q},\) \(S_{0} = – \frac{f_{1}}{2q},\)\(S_{1} = – \frac{f_{1}}{2q},\)\(T_{1} = 0\) in Eq. (11), we get \[\hbar_{1}(x,y,t)=-\frac{f_{1}}{2q}+\frac{f_{1}}{2q}\times \tanh (k_{1}x+k_{2}y+k_{3}t),\] and \[\hbar_{2}(x,y,t)=-\frac{f_{1}}{2q}+\frac{f_{1}}{2q}\times \coth (k_{1}x+k_{2}y+k_{3}t).\] Cluster II: Substituting \(k_{2} = \pm \sqrt{\frac{- 24dqk_{1}^{2} + f_{1}^{2}}{24gq},}\) \(k_{3} = \frac{1}{6}\frac{f_{1}^{2}k_{1}}{q},\) \(S_{0} = – \frac{f_{1}}{2q}\) and \(S_{1} = \frac{f_{1}}{2q},\)\(T_{1} = 0\) in Eq. (11), we get \[\hbar_{3}(x,y,t)=-\frac{f_{1}}{2q}-\frac{f_{1}}{2q}\times \tanh (k_{1}x+k_{2}y+k_{3}t),\] and \[\hbar_{4}(x,y,t)=-\frac{f_{1}}{2q}-\frac{f_{1}}{2q}\times \coth (k_{1}x+k_{2}y+k_{3}t).\] Cluster III: Substituting \(k_{2} = \pm \sqrt{\frac{- \text{96}dqk_{1}^{2} – f_{1}^{2}}{96gq}},\) \(k_{3} = \frac{1}{6}\frac{f_{1}^{2}k_{1}}{q},\) \(S_{0} = – \frac{f_{1}}{2q}\) and \(S_{1} = – \frac{f_{1}}{2q},\)\(T_{1} = \frac{f_{1}}{4q}\) in Eq. (11), we get \[\hbar_{5}(x,y,t)=-\frac{f_{1}}{2q}+\frac{f_{1}}{2q}\times \tanh (k_{1}x+k_{2}y+k_{3}t)+\frac{f_{1}}{4q}\left(\frac{1}{\tanh (k_{1}x+k_{2}y+k_{3}t)}-\tanh (k_{1}x+k_{2}y+k_{3}t)\right),\] and \[\hbar_{6}(x,y,t)=-\frac{f_{1}}{2q}+\frac{f_{1}}{2q}\times \coth (k_{1}x+k_{2}y+k_{3}t)+\frac{f_{1}}{4q}\left(\frac{1}{\tanh (k_{1}x+k_{2}y+k_{3}t)}-\tanh (k_{1}x+k_{2}y+k_{3}t)\right).\] Cluster IV: Substituting \(k_{2} = \pm \sqrt{\frac{- 24dqk_{1}^{2} – f_{1}^{2}}{24gq},}\) \(k_{3} = \frac{1}{6}\frac{f_{1}^{2}k_{1}}{q},\) \(S_{0} = – \frac{f_{1}}{2q}\) and \(S_{1} = – \frac{f_{1}}{2q},\)\(T_{1} = \frac{f_{1}}{2q}\) in Eq. (11), we get \[\hbar_{7}(x,y,t)=-\frac{f_{1}}{2q}+\frac{f_{1}}{2q}\times \tanh (k_{1}x+k_{2}y+k_{3}t)+\frac{f_{1}}{4q}\left(\frac{1}{\tanh (k_{1}x+k_{2}y+k_{3}t)}-\tanh (k_{1}x+k_{2}y+k_{3}t)\right),\] and \[\hbar_{8}(x,y,t)=-\frac{f_{1}}{2q}+\frac{f_{1}}{2q}\times \coth (k_{1}x+k_{2}y+k_{3}t)+\frac{f_{1}}{4q}\left(\frac{1}{\tanh (k_{1}x+k_{2}y+k_{3}t)}-\tanh (k_{1}x+k_{2}y+k_{3}t)\right).\]
In this study, we effectively construct novel solitons and hyperbolic and trigonometric function solutions for the proposed model using the \((\Psi – \Phi)\)-expansion method. This technique is measured as the most recent scheme in this field, which has not been utilized in these equations earlier. For physical analysis, 3-D, 2-D, and contour plots of some of these solutions are comprised of suitable parameters. The obtained solutions discover their application in communication to convey information because solitons can spread over long distances without reduction and without changing their forms. We only included specific figures in this paper to avoid overloading the document. All the developed results are novel and distinct from the reported results. For graphical representation for the studied model, the physical behavior of \(\hbar_{1}(x,y,t)\) using the proper values of parameters \(k_{1} = 2,\) \(f_{1} = – 1,\) \(f_{2} = 1,\) \(y = 1,\) \(q = 2,\) \(d = 5,\) and \(g = 2\) are shown in Figures 2, 3 and 4. The physical behavior of \(\hbar_{2}(x,y,t)\) using the appropriate values of parameters \(k_{1} = 2,\) \(f_{1} = – 1,\) \(f_{2} = 1,\) \(y = 1,\) \(q = 2,\) \(d = 0\text{.}5\) and \(g = 0\text{.}2\) are shown in Figures 5, 6 and 7.
The physical behavior of \(\hbar_{3}(x,y,t)\) using the appropriate values of parameters \(k_{1} = 2,\) \(f_{1} = \text{20},\) \(f_{2} = 1,\) \(y = 1,\) \(q = 2,\) \(d = 1\) and \(g = 2\) are shown in Figures 8, 9 and 10. The physical behavior of \(\hbar_{6}(x,y,t)\) using the appropriate values of parameters \(k_{1} = 2,\) \(f_{1} = – 0\text{.}5,\) \(f_{2} = 1,\) \(y = 1,\) \(q = 2,\) \(d = 1\) and \(g = 2\) are shown in Figures 11, 12 and 13. The physical behavior of \(\hbar_{7}(x,y,t)\) using the appropriate values of parameters \(k_{1} = 2,\) \(f_{1} = – 0\text{.}5,\) \(f_{2} = 1,\) \(y = 1,\) \(q = 2,\) \(d = 5\) and \(g = 2\) are shown in Figures 14, 15 and 16.


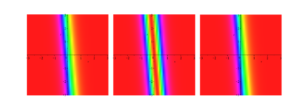


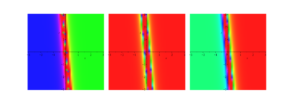

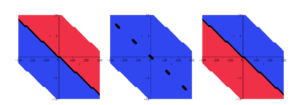
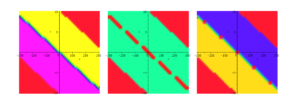


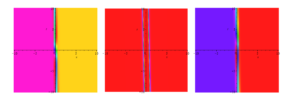


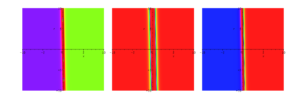
In this paper, we constructed new solitons solutions for the proposed model via the \((\Psi – \Phi)\)-expansion method, in the form of kink, singular kink, bright, dark, mixed bright-dark solitons as well as hyperbolic, rational and trigonometric functions solutions. By choosing the suitable values of parameters and to better underst and the physical structures of the solutions, 3-d, contour and density graphs have been plotted. From the acquired results and figures, it is observed that all solutions demonstrated wave behavior. Also, these solutions yield traveling dark wave behaviors to the considered models, physically.