Topological indices collect information from the graph of molecule and help to predict properties of underlined molecule. Zagreb indices are among the most studied topological indices due to its applications in chemistry. In this report we compute first and second reversed Zagreb indices and first and second reversed Hyper Zagreb indices for \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\). Moreover we also compute first and second reversed Zagreb polynomials and first and second reversed Hyper Zagreb polynomials for \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\).
A graph having no loop or multiple edge in known as simple graph. A molecular graph is a simple graph in which atoms and bonds are represented by vertices and edges respectively. The degree of a vertex is the number of edges attached with it. The maximum degree of vertex among the vertices of a graph is denoted by \(\Delta(G)\). Kulli [1] introduces the concept of reverse vertex degree \(c_{v}\), as \(c_{v}=\Delta(G)-d_{g}(v)+1\).
In discrete mathematics, graph theory in general, not only the study of different properties of objects but it also tells us about objects having same properties as investigating object [2]. In particular, graph polynomials related to graph are rich in information [3, 4, 5, 6, 7, 8].
Mathematical tools like polynomials and topological based numbers have significant importance to collect information about properties of chemical compounds [9, 10, 11]. We can find out many hidden information about compounds through theses tools.
Actually, topological indices are numeric quantities that tells us about the whole structure of graph. There are many topological indices [12, 13, 14, 15] that helps us to study physical, chemical reactivities and biological properties. Wiener [16] in 1947, firstly introduce the concept of topological index while working on boiling point. Hosoya polynomial [3] plays an important role in the area of distance-based topological indices. We can find out Wiener index, Hyper Wiener index and Tratch-stankevich-zefirove index from Hosoya polynomial. Rendić index defined by Milan Rendić [17] in 1975 is one of the oldest degree based topological index and have been extensively studied by mathematician and chemists [18, 19, 20, 21, 22]. Later Gutman et al. introduced the first and second Zagreb indices as:
$$M_{1}(G)=\sum_{uv \in E(G)}(d_{u}+d_{v}),$$ $$ M_{2}(G)=\sum_{uv \in E(G)}(d_{u}.d_{v}).$$ Zagreb indices help us in finding \(\pi\)-electronic energy [23]. Many papers [24, 25, 26, 27], surveys [23, 28, 29] and many modification of Zagreb indices are presented in literture [1, 30, 31, 32, 33, 34]. First and second Zagreb polynomials were defined in [7] as: $$M_{1}(G,x)=\sum_{uv \in E(G)}x^{(d_{u}+d_{v})},$$ $$M_{2}(G,x)=\sum_{uv \in E(G)}x^{(d_{u}.d_{v})}.$$ Motivated by these indices, Shirdel et al. [35] proposed the first and second hyper Zagreb indices as: $$H_{1}(G)=\sum_{uv \in E(G)}(d_{u}+d_{v})^{2},$$ $$H_{2}(G)=\sum_{uv \in E(G)}(d_{u}.d_{v})^{2}.$$ The first and second Reverse Zagreb indices [1] are defined as: $$CM_{1}(G)=\sum_{uv \in E(G)}(c_{u}+c_{v}),$$ $$CM_{2}(G)=\sum_{uv \in E(G)}(c_{u}.c_{v}).$$ The first and second Reverse Hyper Zagreb indices [1] are defined as: $$HCM_{1}(G)=\sum_{uv \in E(G)}(c_{u}+c_{v})^{2},$$ $$HCM_{2}(G)=\sum_{uv \in E(G)}(c_{u}.c_{v})^{2}.$$ With the help of reverse Zagreb and hyper Zagreb indices, we now able to define the reverse Zagreb and reverse hyper Zagreb polynomials as: $$CM_{1}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}+c_{v})}, $$ $$CM_{2}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}.c_{v})},$$ and $$HCM_{1}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}+c_{v})^{2}}, $$ $$ HCM_{2}(G,x)=\sum_{uv \in E(G)}x^{(c_{u}.c_{v})^{2}}.$$ Till now there are more than 148 topological indices and non of them complete describe all properties of understudy molecular compound, so there is always room to define new topological indices. Our aim is to study Silicon Carbide \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\). The multiplicative first and second Zagreb indices, multiplicative hyper Zagreb indices, and some other multiplicative degree-based topological indices of \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\) are computed in [36]. Imran et al. in [37] computed the general Rendić and Zagreb types indices, geometric arithmetic index, atom-bond connectivity index, fourth atom-bond connectivity and fifth geometric arithmetic index of \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II[r,s]\). In this report, we aim to compute reversed first and second Zagreb indices, reversed first and second Hyper Zagreb indices, reversed first and second Zagreb polynomials and reversed first and second Hyper Zagreb polynomials for \(Si_{2}C_{3}I[r,s]\) and \(Si_{2}C_{3}II(G).\) Figures of this paper are taken from [36, 37].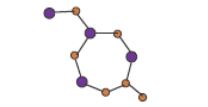
Theorem 3.1.
For the Silicon Carbide \(Si_{2}C_{3}I[r,s]\), the first and second reverse Zagreb indices are:

Proof.
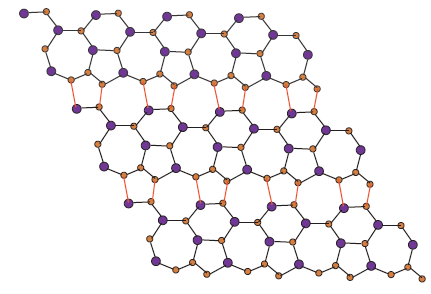
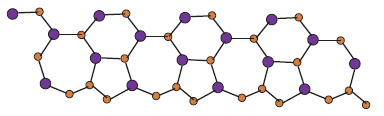
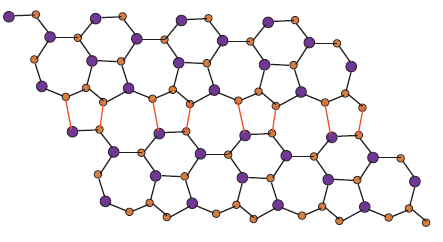
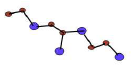
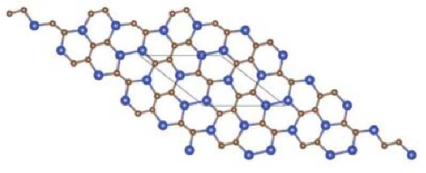
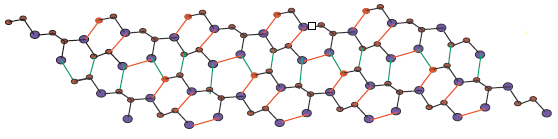
The vertex and edge set of Silicon Carbide is , \(|V(Si_{2}C_{3}I[r,s])|=10rs\) and \(|E(Si_{2}C_{3}I[r,s])|=15rs-2r-3s\), respectively. From figure[1-4], we can say that, there are five type of edges in \(Si_{2}C_{3}I[r,s]\). The edge set of \(Si_{2}C_{3}I[r,s]\) is portioned into the following five edge sets:
$$E_{1}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=1, d_{v}=2\},$$
$$E_{2}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=1, d_{v}=3\},$$
$$E_{3}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=2, d_{v}=2\},$$
$$E_{4}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=2, d_{v}=3\},$$
$$E_{5}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); d_{u}=3, d_{v}=3\},$$
such that, \(|E_{1}(Si_{2}C_{3}I[r,s])|=1\),
\(|E_{2}(Si_{2}C_{3}I[r,s])|=1\),
\(|E_{3}(Si_{2}C_{3}I[r,s])|=r+2s\),
\(|E_{4}(Si_{2}C_{3}I[r,s])|=6r-1+8(s-1) \)
and \(|E_{5}(Si_{2}C_{3}I[r,s])|=15rs-9r-13s+7.\)
As, the maximum degree in \(Si_{2}C_{3}I[r,s]\) is 3, so,
$$c_{u}=\Delta(G)-d_{G}(u)+1= 4-d_{G}(u).$$
The reverse edge set of \(Si_{2}C_{3}I[r,s]\) is given as:
$$CE_{1}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=3, c_{v}=2\},$$
$$CE_{2}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=3, c_{v}=1\},$$
$$CE_{3}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=2, c_{v}=2\},$$
$$CE_{4}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=2, c_{v}=1\},$$
$$CE_{5}(Si_{2}C_{3}I[r,s])=\{uv\in E(Si_{2}C_{3}I[r,s]); c_{u}=1, c_{v}=1\}.$$
And, \(|CE_{1}(Si_{2}C_{3}I[r,s])|=1\),
\(|CE_{2}(Si_{2}C_{3}I[r,s])|=1\),
\(|CE_{3}(Si_{2}C_{3}I[r,s])|=r+2s\),
\( |CE_{4}(Si_{2}C_{3}I[r,s])|=6r-1+8(s-1)\)
and \(|CE_{5}(Si_{2}C_{3}I[r,s])|=15rs-9r-13s+7\).
(1) The first reverse Zagreb index for \(Si_{2}C_{3}I[r,s]\) is:
\begin{eqnarray*}
CM_{1}(Si_{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})\\
&=&(3+2)(1)+(3+1)(1)+(2+2)(r+2s)+(2+1)\\
& &(6r-1+8(s-1))+(1+1)(15rs-9r-13s+7)\\
&=&30rs+4r+6s-4.
\end{eqnarray*}
(2) The second reverse Zagreb index for \(Si_{2}C_{3}I[r,s]\) is:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})\\
&=&(3\cdot2)(1)+(3\cdot1)(1)+(2\cdot2)(r+2s)+(2\cdot1)(6r-1\\
& &+8(s-1))+(1\cdot1)(15rs-9r-13s+7)\\
&=&15rs+7r+9s-2.
\end{eqnarray*}
Theorem 3.2. The first and second reverse Zagreb polynomials for \(Si_{2}C_{3}I[r,s]\) are:
Proof.
Now, by the reverse edge partitions for \(Si_{2}C_{3}I[r,s]\), we have:
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as:
\begin{eqnarray*}
CM_{1}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})}\\
&=&(1)x^{(3+2)}+(1)x^{(3+1)}+(r+2s)x^{(2+2)}+(6r-1\\
& &+8(s-1))x^{(2+1)}+(15rs-9r-13s+7)x^{(1+1)}\\
&=&x^{5}+(r+2s+1)x^{4}+(6r-1+8(s-1))x^{3}\\&&+(15rs-9r-13s+7)x^{2}.
\end{eqnarray*}
(2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})}\\
&=&(1)x^{(3\cdot2)}+(1)x^{(3.1)}+(r+2s)x^{(2\cdot2)}+(6r-1\\
& &+8(s-1))x^{(2\cdot1)}+(15rs-9r-13s+7)x^{(1\cdot1)}\\
&=& x^{6}+(r+2s)x^{4}+x^{3}+(6r-1+8(s-1))x^{2}\\&&+(15rs-9r-13s+7)x.
\end{eqnarray*}
Theorem 3.3. The first and second reverse hyper Zagreb indices of Silicon Carbon \(Si_{2}C_{3}I[r,s]\) are:
Proof.
By reverse edge partition and definition of reverse hyper Zagreb indices, we have:
(1) The first reverse hyper Zagreb index for \(Si_{2}C_{3}I[r,s]\) is:
\begin{eqnarray*}
CM_{1}(Si _{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})^{2}\\
&=&(3+2)^{2}(1)+(3+1)^{2}(1)+(2+2)^{2}(r+2s)+(2+1)^{2}\\
& &(6r-1+8(s-1))+(1+1)^{2}(15rs-9r-13s+7)\\
&=&60rs+34r+50s-12.
\end{eqnarray*}
(2) The second reverse hyper Zagreb index for \(Si_{2}C_{3}I[r,s]\) is:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}I[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})^{2}\\
&=&(3\cdot2)^{2}(1)+(3\cdot1)^{2}(1)+(2\cdot2)^{2}(r+2s)+(2\cdot1)^{2}\\
& &(6r-1+8(s-1))+(1\cdot1)^{2}(15rs-9r-13s+7)\\
&=&15rs+31r+55s-4.
\end{eqnarray*}
Theorem 3.4. The first and second reverse hyper Zagreb polynomials of \(Si_{2}C_{3}$ $I[r,s]\) are:
Proof.
Now, by the reverse edge partitions for \(Si_{2}C_{3}I[r,s]\), we have
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as:
\begin{eqnarray*}
HCM_{1}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})^{2}}\\
&=&(1)x^{(3+2)^{2}}+(1)x^{(3+1)^{2}}+(r+2s)x^{(2+2)^{2}}+(6r-1\\
& &+8(s-1))x^{(2+1)^{2}}+(15rs-9r-13s+7)x^{(1+1)^{2}}\\
&=&x^{25}+(r+2s+1)x^{16}+(6r-1+8(s-1))x^{9}\\&&+(15rs-9r-13s+7)x^{4}.
\end{eqnarray*}
(2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as:
\begin{eqnarray*}
HCM_{2}(Si_{2}C_{3}I[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})^{2}}\\
&=&(1)x^{(3\cdot2)^{2}}+(1)x^{(3\cdot1)^{2}}+(r+2s)x^{(2\cdot2)^{2}}+(6r-1\\
& &+8(s-1))x^{(2\cdot1)^{2}}+(15rs-9r-13s+7)x^{(1\cdot1)^{2}}\\
&=& x^{36}+(r+2s)x^{16}+x^{9}+(6r-1+8(s-1))x^{4}\\&&+(15rs-9r-13s+7)x.
\end{eqnarray*}
| \(r=1,s=1\) | \(r=1,s=2\) | \(r=2,s=1\) | \(r=2,s=1\) | \(r=2,s=3\) | \(r=3,s=3\) | |
|---|---|---|---|---|---|---|
| \(CM_{2}\) | 36 | 72 | 70 | 136 | 202 | 296 |
| \(CM_{2}\) | 29 | 53 | 51 | 90 | 129 | 181 |
| \(HCM_{2}\) | 132 | 242 | 226 | 396 | 566 | 780 |
| \(HCM_{2}\) | 97 | 167 | 143 | 228 | 313 | 389 |
Theorem 3.5. For the Silicon Carbide \(Si_{2}C_{3}II[r,s]\), the first and second reverse Zagreb indices are:
Proof.
The vertex and edge set of Silicon Carbide is, \(|V(Si_{2}C_{3}II[r,s])|=10rs\) and \(|E(Si_{2}C_{3}II[r,s])|=15rs-2r-3s\), respectively. From the Figures 5-8, we can observe that, there are five type of edges in \(Si_{2}C_{3}II[r,s]\). The edge set of \(Si_{2}C_{3}II[r,s]\) is portioned into following five edge sets:
$$E_{1}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=1, d_{v}=2\},$$
$$E_{2}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=1, d_{v}=3\},$$
$$E_{3}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=2, d_{v}=2\},$$
$$E_{4}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=2, d_{v}=3\},$$
$$E_{5}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); d_{u}=3, d_{v}=3\},$$
such that, \(|E_{1}(Si_{2}C_{3}II[r,s])|=2\),
\( |E_{2}(Si_{2}C_{3}II[r,s])|=1\),
\(|E_{3}(Si_{2}C_{3}II[r,s])|=2r+2s\),
\(|E_{4}(Si_{2}C_{3}II[r,s])|=8r+8s-14\)
and \(|E_{5}(Si_{2}C_{3}II[r,s])|=15rs-13r-13s+11.\)
The maximum vertex degree \(Si_{2}C_{3}II[r,s]\) is 3, so,
$$c_{u}=\Delta(G)-d_{G}(u)+1= 4-d_{G}(u).$$
The reverse edge set of \(Si_{2}C_{3}II[r,s]\) is given as:
$$CE_{1}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=3, c_{v}=2\},$$
$$CE_{2}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=3, c_{v}=1\},$$
$$CE_{3}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=2, c_{v}=2\},$$
$$CE_{4}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=2, c_{v}=1\},$$
$$CE_{5}(Si_{2}C_{3}II[r,s])=\{uv\in E(Si_{2}C_{3}II[r,s]); c_{u}=1, c_{v}=1\},$$
and we have, \(|E_{1}(Si_{2}C_{3}II[r,s])|=2\),
\(|E_{2}(Si_{2}C_{3}II[r,s])|=1\),
\( |E_{3}(Si_{2}C_{3}II[r,s])|=2r+2s\),
\(|E_{4}(Si_{2}C_{3}II[r,s])|=8r+8s-14\)
and \(|E_{5}(Si_{2}C_{3}II[r,s])|=15rs-13r-13s+11\).
(1) The first reverse Zagreb index for \(Si_{2}C_{3}II[r,s]\) is:
\begin{eqnarray*}
CM_{1}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})\\
&=&(3+2)(2)+(3+1)(1)+(2+2)(2r+2s)+(2+1)\\
& &(8r+8s-14)+(1+1)(15rs-13r-13s+11)\\
&=&30rs+6r+6s-6.
\end{eqnarray*}
(2) The second reverse Zagreb index for \(Si_{2}C_{3}II[r,s]\) is:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})\\
&=&(3\cdot2)(2)+(3\cdot1)(1)+(2\cdot2)(2r+2s)+(2\cdot1)\\
& &(8r+8s-14)+(1\cdot1)(15rs-13r-13s+11)\\
&=&15rs+11r+11s-2.
\end{eqnarray*}
Theorem 3.6. The first and second reverse Zagreb polynomials for \(Si_{2}C_{3}II[r,s]\) are:
Proof.
Now, by the reverse edge partitions for \(Si_{2}C_{3}II[r,s]\), we have:
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}II[r,s]\), is given as:
\begin{eqnarray*}
CM_{1}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})}\\
&=&(2)x^{(3+2)}+(1)x^{(3+1)}+(2r+2s)x^{(2+2)}+(8r\\
& &+8s-14)x^{(2+1)}+(15rs-13r-13s+11)x^{(1+1)}\\
&=&x^{5}+(2r+2s+1)x^{4}+(8r+8s-14)x^{3}\\&&+(15rs-9r-13s+7)x^{2}.
\end{eqnarray*}
(2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}II[r,s]\), is given as:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})}\\
&=&(2)x^{(3\cdot2)}+(1)x^{(3\cdot1)}+(2r+2s)x^{(2\cdot2)}+(8r\\
& &+8s-14)x^{(2\cdot1)}+(15rs-13r-13s+11)x^{(1.\cdot1)}\\
&=& 2x^{6}+(2r+2s)x^{4}+x^{3}+(8r+8s-14)x^{2}\\&&+(15rs-13r-13s+11)x.
\end{eqnarray*}
Theorem 3.7. The first and second reverse Hyper Zagreb indices of Silicon Carbon \(Si_{2}C_{3}II[r,s]\) are:
Proof.
By reverse edge partition and definition of reverse hyper Zagreb indices, we have:
(1) The first reverse Hyper Zagreb index for \(Si_{2}C_{3}II[r,s]\) is:
\begin{eqnarray*}
CM_{1}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}+c_{v})^{2}\\
&=&(3+2)^{2}(2)+(3+1)^{2}(1)+(2+2)^{2}(2r+2s)+(2+1)^{2}\\
& &(8r+8s-14)+(1+1)^{2}(15rs-13r-13s+11)\\
&=&60rs+52r+52s-16.
\end{eqnarray*}
(2) The second reverse Hyper Zagreb index for \(Si_{2}C_{3}I[r,s]\) is:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}II[r,s])&=&\sum_{uv\in E(G)}(c_{u}.c_{v})^{2}\\
&=&(3+2)^{2}(2)+(3+1)^{2}(1)+(2+2)^{2}(2r+2s)\\
& &+(2+1)^{2}(8r+8s-14)+(1+1)^{2}(15rs\\&&-13r-13s+11)\\
&=&15rs+51r+51s+108.
\end{eqnarray*}
Theorem 3.8. The first and second reverse hyper Zagreb polynomials of \(Si_{2}C_{3}$ $II[r,s]\) is:
Proof.
Now, by the reverse edge partitions for \(Si_{2}C_{3}II[r,s]\), we have:
(1) The first reverse Zagreb polynomial for \(Si_{2}C_{3}II[r,s]\), is given as:
\begin{eqnarray*}
CM_{1}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}+c_{v})^{2}}\\
&=&(2)x^{(3+2)^{2}}+(1)x^{(3+1)^{2}}+(2r+2s)x^{(2+2)^{2}}+(8r\\
& &+8s-14)x^{(2+1)^{2}}+(15rs-13r-13s+11)x^{(1+1)^{2}}\\
&=&2x^{25}+(2r+2s+1)x^{16}+(8r+8s-14)x^{9}\\&&+(15rs-13r-13s+11)x^{4}.
\end{eqnarray*}
(2) The second reverse Zagreb polynomial for \(Si_{2}C_{3}I[r,s]\), is given as:
\begin{eqnarray*}
CM_{2}(Si_{2}C_{3}II[r,s],x)&=&\sum_{uv\in E(G)}x^{(c_{u}.c_{v})^{2}}\\
&=&(2)x^{(3\cdot2)^{2}}+(1)x^{(3\cdot1)^{2}}+(2r+2s)x^{(2\cdot2)^{2}}+(8r+8s\\
& &-14)x^{(2\cdot1)^{2}}+(15rs-13r-13s+11)x^{(1\cdot1)^{2}}\\
&=&2x^{36}+(2r+2s)x^{16}+x^{9}+(8r+8s-14)x^{4}\\&&+(15rs-13r-13s+11)x.
\end{eqnarray*}
| \(r=1,s=1\) | \(r=1,s=2\) | \(r=2,s=1\) | \(r=2,s=1\) | \(r=2,s=3\) | \(r=3,s=3\) | |
|---|---|---|---|---|---|---|
| \(CM_{2}\) | 36 | 72 | 72 | 138 | 204 | 300 |
| \(CM_{2}\) | 35 | 61 | 61 | 162 | 143 | 199 |
| \(HCM_{2}\) | 146 | 257 | 257 | 428 | 599 | 830 |
| \(HCM_{2}\) | 225 | 291 | 291 | 372 | 453 | 549 |