General Zagreb index of some cactus chains

1. Introduction

Chemical graph theory is a branch of mathematical chemistry that has a real world applications to other science, engineering and specially in chemistry. A graph \(G=(V(G),E(G))\) is an ordered pair of two sets where \(V(G)\) denotes the vertex set and \(E(G)\) is the edge set of \(G\). The degree of a vertex \(v\in V(G)\) is the number of vertices other than \(v\) in \(G\) which are adjacent to \(v\) and is denoted by \(d_G(v).\) A topological index of a graph is the numeric quantity obtained from that graph mathematically and is remains same under graph isomorphism. In recent time, there are lot of topological indices discovered by various researchers and these have many applications in chemistry, biochemistry, medical sciences and so forth to understand physicochemical properties of chemical compounds theoretically. A connected graph such that no edge lies in more than one cycle is called the cactus graph. The block of a cactus graph is either an edge or a cycle. If all blocks of a cactus graph are triangular then it is called triangular cactus graph. For a cactus graph, the cut-vertex is a vertex shared by two or more triangles. If all the triangle of a triangular cactus graph has at most two cut-vertices and each cut-vertex is shared by exactly two triangles then we say that triangular cactus graph is a chain triangular cactus. In chain triangular cactus if we replace triangles by cycles of length 4 then we obtain cacti whose every block is \(C_4\), such cacti are called square cacti. For ortho-chain square cactus the cut vertices are adjacent and a para-chain square cactus their cut vertices are not adjacent. Recently, Sadeghieh et al. in [1] derived Hosoya polynomial of some cactus chain and studied some degree based topological indices. we refer the reader [2, 3, 4, 5] for further study about cactus graph. In this work, we study the mathematical property of general Zagreb index or \((a,b)\)-Zagreb index of some general ortho and para cactus chains and hence consider their special cases such as triangular chain cactus \(T_n\), ortho chain square cactus \(O_n\) and para-chain square cactus \(Q_n\), where \(n\) denote the length of the chain and then we derive some explicit expressions of the same for other degree based topological indices such as Zagreb indices, forgotten index, redefined Zagreb index, general first Zagreb index, general Randić index, symmetric division index for particular values of \(a\) and \(b\) of general Zagreb index.

Gutman and Trinajstić [6] introduced the Zagreb indices, to study the total \(\pi\)-electron energy of carbon atoms and are defined as \[{{M}_{1}}(G)=\sum\limits_{v\in V(G)}{{{d}_{G}}{{(v)}^{2}}}=\sum\limits_{uv\in E(G)}{[{{d}_{G}}(u)+{{d}_{G}}(v)]}\] and \[{{M}_{2}}(G)=\sum\limits_{uv\in E(G)}{{{d}_{G}}(u){{d}_{G}}(v)}.\] In the same paper [6], the “forgotten topological index” or F-index was defined as \[{F}(G)=\sum\limits_{v\in V(G)}{{{d}_{G}}{{(v)}^{3}}}=\sum\limits_{uv\in E(G)}{[{{d}_{G}}(u)^2+{{d}_{G}}(v)^2]}.\] In 2003, Ranjini et al. redefined the Zagreb index in [7], and is defined as \[{{ReZM}}(G)=\sum\limits_{uv\in E(G)}{{{d}_{G}}(u){{d}_{G}}(v)[{{d}_{G}}(u)+{{d}_{G}}(v)]}.\] Li and Zheng [8], introduced the general Zagreb index as \[M^{\alpha}(G)=\sum_{u\in V(G)}d_G(u)^{\alpha}\] where, \(\alpha \neq 0,1\) and \(\alpha \in { I\!R}\). Clearly, when \(\alpha =2\) we get first Zagreb index and when \(\alpha =3\) it gives the F-index. Gutman and Lepovi\'{c} [9], generalized the Randi\'{c} index in 2001 as \[R_{a}=\sum\limits_{uv\in E(G)}\{d_G(u).d_G(v)\}^{a}\] where, \(a \neq 0,~a \in { I\!R}\). The symmetric division index of a graph is defined as \[SDD(G)=\sum\limits_{uv\in E(G)}[\frac{d_G(u)}{d_G(v)}+\frac{d_G(v)}{d_G(u)}].\] For further study about this index, we refer [10, 11, 12]. In 2011, Azari et al. [13], introduced a generalized version of vertex degree based topological index, named as generalized Zagreb index or the \((a,b)\)-Zagreb index and is defined as \[M_{a,b}(G)=\sum\limits_{uv\in E(G)}(d_G(u)^ad_G(v)^b+d_G(u)^bd_G(v)^a).\] We refer [14, 15, 16, 17, 18] for further study about this index.

It is clear that, all the topological indices discussed previously, can be obtained from \((a,b)\)-Zagreb index for some particular values of \(a\) and \(b\). The Table 1, shows the relationship between \((a,b)\)-Zagreb index with other topological indices.

Table 1.Relations between (a,b)-Zagreb index with some other topological indices.

\((d_{u},d_{v})\) where \(uv\in E(\mathcal{H})\)	\(\text{Number of edges}\)
\(\mathrm{E_1}=(3,5)\)	\(12\)
\(\mathrm{E_2}=(3,7)\)	\(18n-36\)
\(\mathrm{E_3}=(3,12)\)	\(18n^2-54n+42\)
\(\mathrm{E_4}=(5,7)\)	\(12\)
\(\mathrm{E_5}=(5,12)\)	\(6\)
\(\mathrm{E_6}=(7,7)\)	\(6n-18\)
\(\mathrm{E_7}=(7,12)\)	\(12n-24\)
\(\mathrm{E_8}=(12,12)\)	\(9n^2-33n+30\)

2. Main Results

In this section, we consider two general cactus chains namely para cacti chain and ortho cacti chain of cycles. We first consider a para cacti chain of cycles \(C_m\) of length \(n\), where every block is a cycle \(C_m\). Let it is denoted by \(C_m^n\). In the following theorem we compute an exact expression of general Zagreb index of \(C_m^n\). Note that, the total number of vertices of \(C_m^n\) are \((mn-n+1)\) and the number of edges of \(C_m^n\) are \(mn.\)

Theorem 1. Let \(C_m^n\) be the para cacti chain of cycles for \((m\ge 3,~n\ge 2)\). Then \begin{eqnarray*} M_{a,b}(C_m^n)&=&4(n-1)2^{a+b}(2^a+2^b)+(mn-4n+4).2^{a+b+1}. \end{eqnarray*}

Proof. The edge set of \(C_m^n\) can be partitioned into following subsets: \[E_1(C_m^n)=\{e=uv:d_{C_m^n}(u)=d_{C_m^n}(v)=2\},\] \[E_2(C_m^n)=\{e=uv:d_{C_m^n}(u)=2,~ d_{C_m^n}(v)=4\},\] such that \[|E_1(C_m^n)|=2(m-2)+(m-4)(n-2),~|E_2(C_m^n)|=4(n-1).\] Then from definition of general Zagreb index, we have \begin{eqnarray*} M_{a,b}(C_m^n)&=&\sum\limits_{uv\in E(C_m^n)}(d_{C_m^n}(u)^ad_{C_m^n}(v)^b+d_{C_m^n}(u)^bd_{C_m^n}(v)^a)\\ &=&\sum\limits_{uv\in E_1(C_m^n)}(2^a2^b+2^b2^a)+\sum\limits_{uv\in E_2(C_m^n)}(2^a4^b+2^b4^a)\\ &=&|E_1(C_m^n)|(2^a2^b+2^b2^a)+|E_2(C_m^n)|(2^a4^b+2^b4^a)\\ &=&2[(m-2)+(m-4)(n-2)].2.2^{a+b}+4(n-1).2^{a+b}(2^a+2^b), \end{eqnarray*} from where the result follows.

Following results follows immediately form Theorem 1.

Corollary 2. Let \(C_m^n\) be the para cacti chain of cycles for \((m\ge 3,~n\ge 2)\). Then

1. \(M_1(C_m^n)=M_{1,0}(C_m^n)=4mn+8n-8.\)
2. \(M_2(C_m^n)=\frac{1}{2} M_{1,1}(C_m^n)=4mn+16n-16.\)
3. \(F(C_m^n)=M_{2,0}(C_m^n)=8mn+48n-48.\)
4. \(ReZM(C_m^n)=M_{2,1}(C_m^n)=16mn+128n-128.\)
5. \(^a(C_m^n)=M_{a-1,0}(C_m^n)=(n-1).2^{a+1}(2^{a-1}+1)+2^a(mn-4n+4).\)
6. \(R_a(C_m^n)=\frac{1}{2} M_{a,a}(C_m^n)=(n-1).2^{3a+2}+(mn-4n+4)2^{2a}.\)
7. \(SDD(C_m^n)=M_{1,-1}(C_m^n)=2mn+2n-2.\)

The results about para square cactus chain \(Q_n\) can be obtained from Theorem 1 by taking \(m=4.\) The representation of \(Q_n\) depicted in the Figure 1.

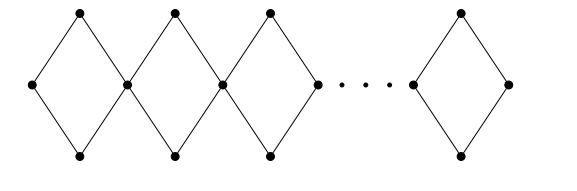
Corollary 3. Let \(Q_n\) be the para-chain square cactus graph for \(n\ge 2.\) Then \begin{eqnarray*} M_{a,b}(Q_n)&=&2^{a+b+3}+(n-1).2^{a+b+2}(2^a+2^b). \end{eqnarray*}

Proof. If we put \(m=4\) in Theorem 1, we get our desired result.

Following results can be immediately obtained from Corollary 3.

Corollary 4.Let \(Q_n\) be the para-chain square cactus graph for \(n\ge 2.\) Then

1. \(M_1(Q_n)=M_{1,0}(Q_n)=24n-8.\)
2. \(M_2(Q_n)=\frac{1}{2} M_{1,1}(Q_n)=32n-16.\)
3. \( F(Q_n)=M_{2,0}(Q_n)=80n-48.\)
4. \( ReZM(Q_n)=M_{2,1}(Q_n)=192n-128.\)
5. \( M^a(Q_n)=M_{a-1,0}(Q_n)=2^{a+2}+(n-1)(2^{2a}+2^{a+1}).\)
6. \( R_a(Q_n)=\frac{1}{2} M_{a,a}(Q_n)=2^{2a+2}+(n-1).2^{3a+2}.\)
7. \( SDD(Q_n)=M_{1,-1}(Q_n)=10n-2.\)

The generalized Zagreb index of the para-chain hexagonal cactus graph \(L_n~n\ge 3\) can be obtained from Theorem 1 by putting \(m=6\). The para-chain hexagonal cactus graph is shown in Figure 2.

Corollary 5. Let \(L_n\) be the para-chain hexagonal cactus graph for \(n\ge 3.\) Then \begin{eqnarray*} M_{a,b}(L_n)&=&(n+2)2^{a+b+2}+(n-1)2^{a+b+2}(2^a+2^b). \end{eqnarray*}

Proof. If we put \(m=6\) in Theorem 1, we get our desired result.

Following results follows form Corollary 5.

Corollary 6. Let \(L_n\) be the para-chain hexagonal cactus graph for \(n\ge 3.\) Then

1. \(M_1(L_n)=M_{1,0}(L_n)=32n-8.\)
2. \(M_2(L_n)=\frac{1}{2} M_{1,1}(L_n)=40n-16.\)
3. \(F(L_n)=M_{2,0}(L_n)=96n-48.\)
4. \(ReZM(L_n)=M_{2,1}(L_n)=256n-128.\)
5. \(M^a(L_n)=M_{a-1,0}(L_n)=2^{a+1}(2n+1)+(n-1).2^{2a}.\)
item \(R_a(L_n)=\frac{1}{2} M_{a,a}(L_n)=2^{2a+1}(n+2)+(n-1).2^{3a+2}.\)
6. \(SDD(L_n)=M_{1,-1}(L_n)=14n-2.\)

Next, we consider the ortho-chain cactus of cycles where its cut-vertices are adjacent. Let, this type of cactus chain is denoted by \(CO_m^n\) where \(m\) is the length of each cycle and \(n\) is the length of the chain. The number of vertices and edges of \(CO_m^n\) are \(mn-n+1\) and \(mn\) respectively. In the following theorem, we calculate the general Zagreb index of \(CO_m^n\).

Theorem 7. Let \(CO_m^n\) be the ortho cacti chain of cycles for \((m\ge 3,~n\ge 2).\) Then \begin{eqnarray*} M_{a,b}(CO_m^n)&=&2(n-2)4^{a+b}+(mn-3n+2)\cdot2^{a+b+1}+n\cdot2^{a+b+1}(2^a+2^b). \end{eqnarray*}

Proof. The edge set of \(CO_m^n\) can be partitioned into following subsets: \[E_1(CO_m^n)=\{e=uv:d_{CO_m^n}(u)=d_{CO_m^n}(v)=4\},\] \[E_2(CO_m^n)=\{e=uv:d_{CO_m^n}(u)=2,~ d_{CO_m^n}(v)=4\},\] \[E_3(CO_m^n)=\{e=uv:d_{CO_m^n}(u)=d_{CO_m^n}(v)=2\}.\] Now, \[|E_1(CO_m^n)|=(n-1),~|E_2(CO_m^n)|=2n,~|E_3(CO_m^n)|=2(m-2)+(m-3)(n-2).\] Therefore, from definition of general Zagreb index, we have \begin{eqnarray*} M_{a,b}(CO_m^n)&=&\sum\limits_{uv\in E(CO_m^n)}(d_{CO_m^n}(u)^ad_{CO_m^n}(v)^b+d_{CO_m^n}(u)^bd_{CO_m^n}(v)^a)\\ &=&\sum\limits_{uv\in E_1(CO_m^n)}(4^a4^b+4^b4^a)+\sum\limits_{uv\in E_2(CO_m^n)}(2^a4^b+2^b4^a)+\sum\limits_{uv\in E_3(CO_m^n)}(2^a2^b+2^b2^a)\\ &=&|E_1(CO_m^n)|(4^a4^b+4^b4^a)+|E_2(CO_m^n)|(2^a4^b+2^b4^a)+|E_3(CO_m^n)|(2^a2^b+2^b2^a)\\ &=&2(n-2)4^{a+b}+2n.2^{a+b}(2^a+2^b)+2[2(m-2)+(m-3)(n-2)]2^{a+b}, \end{eqnarray*} from where the desired result follows.

Following results follows immediately form Theorem 7.

Corollary 8. Let \(CO_m^n\) be the ortho cacti chain of cycles for \((m\ge 3,~n\ge 2).\) Then

1. \(M_1(CO_m^n)=M_{1,0}(CO_m^n)=4mn+8n-8.\)
2. \(M_2(CO_m^n)=\frac{1}{2} M_{1,1}(CO_m^n)=4mn+20n-24.\)
3. \(F(CO_m^n)=M_{2,0}(CO_m^n)=8mn+48n-48.\)
4. \(ReZM(CO_m^n)=M_{2,1}(CO_m^n)=16mn+176n-224.\)
5. \(M^a(CO_m^n)=M_{a-1,0}(CO_m^n)=2(n-2)4^{a-1}+2^{a}(mn-3n+2)+n\cdot2^a(2^{a-1}+1).\)
6. \(R_a(CO_m^n)=\frac{1}{2} M_{a,a}(CO_m^n)=(n-2)4^{2a}+2^{2a}(mn-3n+2)+n.2^{3a+1}.\)
7. \(SDD(CO_m^n)=M_{1,-1}(CO_m^n)=2mn+n.\)

Now, we consider chain triangular cactus as shown in Figure 3, denoted by \(T_n\), where \(n\) is the length of the chain triangular cactus. \(T_n\) is special case of \(CO_m^n\) for \(m=3.\)

Corollary 9. Let \(T_n\) be the chain triangular cactus for \(n\ge 2.\) Then \begin{eqnarray*} M_{a,b}(T_n)&=&2^{a+b+2}+n\cdot2^{a+b+1}(2^a+2^b)+2(n-2)4^{a+b}. \end{eqnarray*}

Proof. If we put \(m=3\) in Theorem 7, we get our desired result.

Following results follows immediately form Corollary 9.

Corollary 10. Let \(T_n\) be the chain triangular cactus for \(n\ge 2.\) Then

1. \(M_1(T_n)=M_{1,0}(T_n)=20n-8.\)
2. \(M_2(T_n)=\frac{1}{2} M_{1,1}(T_n)=32n-24.\)
3. \(F(T_n)=M_{2,0}(T_n)=72n-48.\)
4. \(ReZM(T_n)=M_{2,1}(T_n)=224(n-1).\)
5. \(M^a(T_n)=M_{a-1,0}(T_n)=2^{a+1}+n\cdot2^a(2^{a-1}+1)+2(n-2)4^{a-1}.\)
6. \(R_a(T_n)=\frac{1}{2} M_{a,a}(T_n)=2^{2a+1}+n\cdot2^{3a+1}+(n-2)4^{2a}.\)
7. \(SDD(T_n)=M_{1,-1}(T_n)=7n.\)

Next, we consider square chain cacti, which is obtained by replacing triangles in \(T_n\) by cycle of length 4. The square chain cacti is denoted by \(O_n\) where \(n\) is the length of the chain as shown in Figure 4.

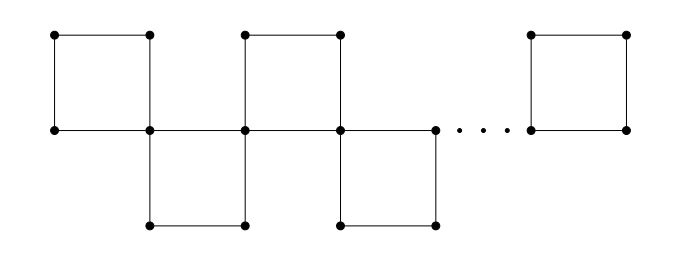
Corollary 11. Let \(O_n\) be the ortho-chain for \(n\ge 2.\) Then \begin{eqnarray*} M_{a,b}(O_n)&=&(n+2)\cdot2^{a+b+1}+n\cdot2^{a+b+1}(2^a+2^b)+2(n-2)4^{a+b}. \end{eqnarray*}

Proof. If we put \(m=4\) in Theorem 7, we get our desired result.

Following results follows immediately form Corollary 11.

Corollary 12. Let \(O_n\) be the ortho-chain for \(n\ge 2.\) Then

1. \(M_1(O_n)=M_{1,0}(O_n)=24n-8.\)
2. \(M_2(O_n)=\frac{1}{2} M_{1,1}(O_n)=36n-24.\)
3. \(F(O_n)=M_{2,0}(O_n)=80n-48.\)
4. \(ReZM(O_n)=M_{2,1}(O_n)=240n-224.\)
5. \(M^a(O_n) =M_{a-1,0}(O_n)=(n+2)\cdot2^a+n\cdot2^a\cdot(2^{a-1}+1)+2(n-2)4^{a-1}.\)
6. \(R_a(O_n)=\frac{1}{2} M_{a,a}(O_n)=(n+2)\cdot2^{2a}+n\cdot2^{3a+1}+(n-2)4^{2a}.\)
7. \(SDD(O_n)=M_{1,-1}(O_n)=9n.\)

The graph \(Q(m,n)\) is derived from \(K_m\) and \(m\) copies of \(K_n\) by identifying every vertex of \(K_m\) with a vertex of one \(K_n\) [5]. The example of \(Q(m,n)\) graph is shown in Figure 5. Here, we compute the general Zagreb index of the graph \(Q(m,n)\) and derive some other topological indices from it.

Theorem 13. Let \(Q(m,n)\) be the ortho-chain for \(m,n\ge 2.\) Then \begin{eqnarray*} M_{a,b}(Q(m,n))&=&m(n-2)\cdot(n-1)^{a+b+1}+m(m+n-2)^b(n-1)^{a+1}\\ &&+m(n-1)^{b+1}(m+n-2)^a+m(n-1)(m+n-2)^{a+b}. \end{eqnarray*}

Proof. The edge set of ortho-chain \(Q(m,n)\) can be partitioned into the following subsets: \[E_1(Q(m,n))=\{e=uv:d_{Q(m,n)}(u)=d_{Q(m,n)}(v)=(n-1)\},\] \[E_2(Q(m,n))=\{e=uv:d_{Q(m,n)}(u)=(n-1),~ d_{Q(m,n)}(v)=(m+n-2)\},\] \[E_3(Q(m,n))=\{e=uv:d_{Q(m,n)}(u)=d_{Q(m,n)}(v)=(m+n-2)\}.\] Such that \[|E_1(Q(m,n))|=\frac{m(n-1)(n-2)}{2},~|E_2(Q(m,n))|=m(n-1),~|E_3(Q(m,n))|=\frac{m(n-1)}{2}.\] Therefore, using the definition of general Zagreb index, we have \begin{eqnarray*} M_{a,b}(Q(m,n))&=&\sum\limits_{uv\in E(Q(m,n))}[d_{Q(m,n)}(u)^ad_{Q(m,n)}(v)^b+d_{Q(m,n)}(u)^bd_{Q(m,n)}(v)^a]\\ &=&\sum\limits_{uv\in E_1(Q(m,n))}[(n-1)^a(n-1)^b+(n-1)^b(n-1)^a]\\ &&+\sum\limits_{uv\in E_2(Q(m,n))}[(n-1)^a(m+n-2)^b+(n-1)^b(m+n-2)^a]\\ &&+\sum\limits_{uv\in E_3(Q(m,n))}[(m+n-2)^a(m+n-2)^b+(m+n-2)^b(m+n-2)^a]\\ &=&|E_1(Q(m,n))|[(n-1)^a(n-1)^b+(n-1)^b(n-1)^a]\\&&+|E_2(Q(m,n))|[(n-1)^a(n-1)^b+(n-1)^b(n-1)^a]\\ &&+|E_3(Q(m,n))|[(m+n-2)^a(m+n-2)^b+(m+n-2)^b(m+n-2)^a]\\ &=&\frac{m(n-1)(n-2)}{2}\cdot2\cdot(n-1)^{a+b}+m(n-1)[(n-1)^a(m+n-2)^b+(n-1)^b(m+n-2)^a]\\ &&+\frac{m(n-1)}{2}\cdot2\cdot(m+n-2)^{a+b}. \end{eqnarray*}

Following results follows immediately from Theorem 13.

Corollary 14. Let \(Q(m,n)\) be the ortho-chain for \(m,n\ge 2.\) Then

1. \(M_1(Q(m,n))=M_{1,0}(Q(m,n))=m(n-1)^3+2m(n-1)(m+n-2).\)
2. \(M_2(Q(m,n))=\frac{1}{2} M_{1,1}(Q(m,n))=\frac{1}{2}[m(n-2)(n-1)^3+2m(n-1)^2(m+n-2)+m(n-1)(m+n-2)^2.\)
3. \(F(Q(m,n))=M_{2,0}(Q(m,n))=m(n-2)(n-1)^3+m(n-1)^3+2m(n-1)(m+n-2)^2.\)
4. \(ReZM(Q(m,n))=M_{2,1}(Q(m,n))=m(n-2)(n-1)^4+m(m+n-2)(n-1)^3+m(n-2)^2(m+n-2)^2+m(n-1)(m+n-2)^3.\)
5. \(M^a(Q(m,n))=M_{a-1,0}(Q(m,n))=m(n-1)^{a+1}+2m(n-1)(m+n-2)^{a-1}.\)
6. \(R_a(Q(m,n))=\frac{1}{2} M_{a,a}(Q(m,n))=\frac{1}{2}[m(n-2)(n-1)^{2a+1}+2m(n-1)^{a+1}(m+n-2)^a+m(n-1)(m+n-2)^{2a}].\)
7. \(SDD(Q(m,n))=M_{1,-1}(Q(m,n))=m(n-2)(n-1)+m(m+n-2)^{-1}(n-1)^2+m(m+n-2)+m(n-1).\)

3. Conclusions

In this study, we obtain some closed expressions of the general Zagreb index of some cactus chain and hence obtain some other important degree based topological indices for some particular values of \(a\) and \(b\). For further study the general Zagreb index of some other graph structures can be computed.

Competing Interests

The authors declare that they have no competing interests.