Wiener index of uniform hypergraphs induced by trees

1. Introduction

In this paper we are concerned with undirected connected graphs \(G\) with vertex set \(V(G)\) and edge set \(E(G)\). The degree of a vertex is the number of edges that are incident to the vertex. Degree of a vertex \(v\) is denoted by \(\deg(v)\). If \(u\) and \(v\) are vertices of \(G\), then the number of edges in a shortest path connecting them is said to be their distance and is denoted by \(d_G(u,v)\). Distance of a vertex \(v\) is the sum of distances from \(v\) to all vertices of a graph, \(d_G(v)=\sum_{u\in V(G)} d(v,u)\). The Wiener index is a graph invariant defined as the sum of distances between all vertices of \(G\): $$ W(G)= \sum_{u,v \in V(G)} d(u,v)=\frac12 \sum_{v \in V(G)} d_G(v). $$

It was introduced as a structural descriptor for tree-like molecular graphs [1]. Details on the mathematical properties and chemical applications of the Wiener index can be found in books [2, 3, 4, 5, 6, 7] and reviews [8, 9, 10, 11, 12, 13]. A number of articles are devoted to comparing of the index of a graph and its derived graphs such as the line graph, the total graph, thorny and subdivision graphs of various kind (see, for example, [14, 15, 16, 17]). Hypergraphs generalize graphs by extending the definition of an edge from a binary to an \(r\)-ary relation. Wiener index of some classes of hypergraphs was studied in [18, 19, 20]. Chemical applications of hypergraphs were discussed in [21, 22].

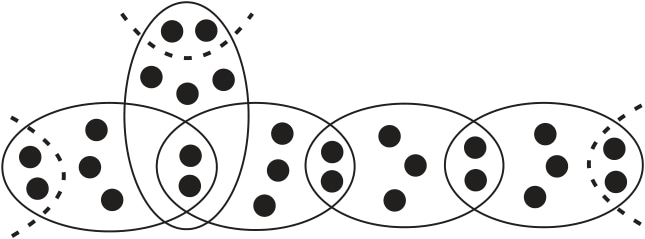
Define a class of \(r\)-uniform hypergraphs \(H_{r,k}(T)\) induced by \(n\)-vertex trees \(T\). Edges of a tree correspond to hyperedges of cardinality \(r\) and adjacent hyperedges have \(k\) vertices in common, \(1 \leq k \leq \lfloor r/2\rfloor\). Examples of a tree and the corresponding hypergraph are shown in Figure 1. The number of vertices of \(H_{r,k}(T)\) is equal to \((n-2)(r-k)+r\). We are interesting in finding a relation between quantities \(W(T)\) and \(W(H_{r,k}(T))\).

2. Main result

Wiener indices of a tree and its induced hypergraph satisfy the following relation.

Theorem 1. For the induced hypergraph \(H_{r,k}(T)\) of a tree \(T\) with \(n\) vertices, $$ W(H_{r,k}(T)) = (r-k)^2\,W(T) + n\binom{k}{2} – (n-1)\binom{r-2k+1}{2}. $$

This result may be useful for ordering of Wiener indices of hypergraphs. If \(r\) and \(k\) are fixed, then the ordering of the Wiener index of induced hypergraphs \(H_{r,k}\) for \(n\)-vertex trees is completely defined by the ordering of the index of trees. In particular, $$ W(H_{r,k}(S_n)) \le W(H_{r,k}(T)) \le W(H_{r,k}(P_n)) $$ for any \(n\)-vertex tree \(T\), where \(S_n\) and \(P_n\) are the star and the path with \(n\) vertices, $$ W(H_{r,k}(S_n)) = \big( r(n-1)[2n(r – 2k) + 8k – 3r – 1] + k(n-2)[k(2n-3)+1] \big) /2, $$ $$ W(H_{r,k}(P_n)) = n(r-k)[(r-k)n^2 + 10k -4r-3]/6 + 2k^2-k(2r+1)+ r(r+1)/2. $$

3. Proof of Theorem 1.

The edge subdivision operation for an edge \((x,y)\in E(G)\) is the deletion of \((x,y)\) from graph \(G\) and the addition of two edges \((x,v)\) and \((v,y)\) along with the new vertex \(v\). Vertex \(v\) is called the subdivision vertex. Denote by \(T_e\) the tree obtained from the subdivision of edge \(e\) in a tree \(T\). The distance \(d_G(v,U)\) from a vertex \(v \in V(G)\) to a vertex subset \(U \subseteq V(G)\) is defined as \(d_G(v,U)=\sum_{u\in U} d_G(v,u)\).

Lemma 2. Let \(T_{e_1}, T_{e_2}, \dots , T_{e_{n-1}}\) be trees obtained by subdivision of edges \(e_1, e_2, \dots, e_{n-1}\) of \(n\)-vertex tree \(T\) with subdivision vertices \(v_1, v_2, \dots , v_{n-1}\), respectively. Then $$ d_{T_{e_1}}(v_{1}) + d_{T_{e_2}}(v_{2}) + \dots + d_{T_{e_{n-1}}}(v_{{n-1}}) = 2W(T). $$

Proof. Let \(v\) be the subdivision vertex of edge \(e=(x,y)\) of a tree \(T\). Denote by \(V_x\) and \(V_y\) the sets of vertices of two connected components after deleting edge \(e\) from \(T\) where \(x \in V_x\) and \(y \in V_y\). Since \(d_T(x)=d_T(x,V_x) + |V_y| + d_T(y,V_y)\) and \(d_T(y)=d_T(y,V_y) + |V_x| + d_T(x,V_x)\), \(d_T(x,V_x) + d_T(y,V_y) = (d_T(x) + d_T(y) – n)/2\). Then \begin{eqnarray*} d_{T_e}(v) & = & \sum_{u \in V_x} [\,d_{T_e}(v,x) + d_{T}(x,u)\,] + \sum_{u \in V_y} [\,d_{T_e}(v,y) + d_{T}(y,u)\,] \\ & = & d_T(x,V_x) + d_T(y,V_y) + n = (d_T(x) + d_T(y) + n)/2. \end{eqnarray*} Klein et al. [23] proved that \(\sum_{v \in V(T)} \deg(v) d_T(v) = 4W(T) – n(n-1)\) for an arbitrary \(n\)-vertex tree \(T\). Then \begin{eqnarray*} 2\sum_{i =1}^{n-1} d_{T_{e_i}}(v_i) & = & \sum_{(x,y) \in E(T)} (d_T(x) + d_T(y) + n) \\ &= & \sum_{v \in V(T)} \deg(v) d_T(v)+n(n-1) = 4W(T). \\[-10mm] \end{eqnarray*}

For convenience, we assume that pendent hyperedges are also adjacent with fictitious hyperedges shown by dashed lines in Figure 2. Denote by \(B_i\), \(i=1,2,\dots n\), the vertices of a hypergraph \(H=H_{r,k}(T)\) belonging to hyperedge intersections and let \(A = V(H) \setminus B_1 \cup B_2 \cup \dots \cup B_n\). We assume that edge \(E_i\) of the induced hypergraph corresponds to edge \(e_i\) of the source tree \(T\), \(i=1,2,\dots ,n-1\). Let \(d_G(U)=\sum_{u\in U} d_G(u)\) for \(U \subseteq V(G)\). Then the Wiener index of \(H\) can be represented as follows:

Let \(u\in E_i \cap A\) and \(v_i\) be the subdivision vertex of edge \(e_i\) in \(T\), \(i=1,2,\dots ,n-1\). Then \begin{eqnarray*} d_H(u) & = & (r-2k-1) + k + k + 2(r-k)+ \dots + 2(r-k) + 3(r-k)+ \dots + 3(r-k) + \dots \\ & = & (r-2k-1) – 2(r-2k) + (r-k) + (r-k) + 2(r-k)+ \dots + 2(r-k) \\ & & \mbox{} + 3(r-k)+ \dots + 3(r-k) + 4(r-k)+ \dots + 4(r-k) + \dots \\ & = & (r-k)d_{T_{e_i}}(v_i) – 2(r-2k) + (r-2k-1). \end{eqnarray*} Summing this equality for all vertices of intersection \(E_i \cap A\), we have \(d_H(E_i \cap A)=(r-2k)d_H(u)=(r-2k)[(r-k)d_{T_{e_i}}(v_i) -(r-2k+1)]\). Applying Lemma 1, we can write Let \(u\in B_i\) and vertex \(v_i\) of \(T\) corresponds to this hyperedge intersection, \(i=1,2,\dots ,n\). Then \begin{eqnarray*} d_H(u) & = & (k-1) + (r-k)+ \dots + (r-k) + 2(r-k) + \dots + 2(r-k) + 3(r-k)+ \dots + 3(r-k) + \dots \\ & = & (r-k)d_T(v_i) + (k-1). \end{eqnarray*} Summing this equality for all vertices of the hyperedge intersection \(B_i\), we have \(d_H(B_i)=k d_H(u)=k[\, (r-k)d_T(v_i) + (k-1)\, ]\). For vertices of all intersections, Substitution expressions (2) and (3) back into Equation (1) completes the proof.

Acknowledgments

This work is supported by the Russian Foundation for Basic Research(project numbers 19-01-00682 and 17-51-560008).

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

The authors declare no conflict of interest.