The inverse sum indeg index (\(ISI\)) and \(ISI\) energy of Hyaluronic Acid-Paclitaxel molecules used in anticancer drugs

1. Introduction

Let \(G(V,E)\) be a simple connected graph where \(V\) is vertex set and \(E\) is edge set. The cardinality of the vertex set of a graph is denoted by \(n\) and the cardinality of its edge set is denoted by \(m\). An edge \(e=uv\) of this graph connects the vertices \(u\) and \(v\). The degree of a vertex \(u\) is denoted by \(d_{u}\) and is defined in [1].

A molecular graph represents the skeletons of nonsaturated hydrocarbon of molecules and molecular compounds. The vertices and edges of this graph correspond to non-hydrogen atoms and covalent bonds between atoms, respectively. Note that hydrogen atoms are often omitted. Chemical graph theory deals with the energy levels of electrons in a molecular which is the eigenvalues of the graph and the strength of particles which is the spectrum of the graph [2,3]. Topological indices are numerical descriptors of a molecular graph. They are used to predict the physicochemical and bioactivity properties of molecules and molecular compounds [4,5,6].

The Wiener index which was introduced by Harold Wiener is the oldest topological index. This index was used for the physical properties of paraffin [7]. Topological indices can be classified according to the structural features of the graph. For example, the Wiener index which is based on the distance between vertices, the Randic and the Zagreb indices which are based on degree, the Estrada index which is based on the spectrum of a graph, the Hosaya index which is based on the matching, the bond-additive indices which are based measure of peripherality in graphs [4].

Hyaluronic acid (HA) which is a major component of the extracellular matrix and a naturally-occurring glycosaminoglycan is a promising molecule for use in drug production due to its biodegradable, non-toxic, hydrophilic, biocompatible, non -immutable features and unique [8]. Therefore, HA has attracted great attention in pharmaceutical production. In recent years, many scientists have shown that the use of HA in the production of anticancer drugs helps the treatment [9,10,11]. It has been observed that HA can be useful in the treatment of heart diseases [12]. Figure 1 shows the molecular graph of Hyaluronic acid and Figure 2 shows the molecular graph of Hyaluronic Acid-Paclitaxel (HA-PTX) conjugates with \(n=3\).

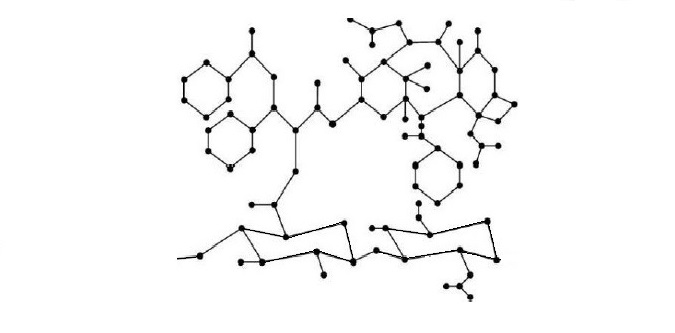
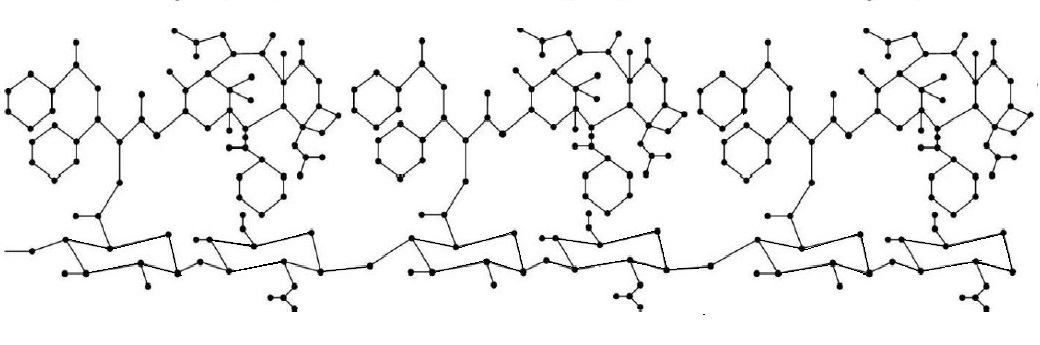
Since the experiments are costly and time-consuming, it has been necessary to calculate topological indices that give information about the topology (physical chemistry and biological properties) of the molecule and molecular compounds. Many scientists studied the topological indices of HA and HA-PTX conjugates [8,13,14]. Many studies have been conducted in chemistry and pharmaceutical science since it is useful to calculate the topological indices of molecules [15,16,17,18,19,20,21,22,23,24,25].

Gutman and Trinajtic defined first Zagreb index in [26] as

\begin{equation*} M_{1}(G)=\underset{u\in V(G)}{\sum }d_{u}^{2}=\underset{uv\in E\left( G\right) }{\sum }d_{u}+d_{v}. \end{equation*} Vukicevic and Gasperov introduced the discrete Adriatic indices which are bond-additive indices [27]. One of these indices is inverse sum indeg index which is defined as The inverse sum indeg adjacency matrix \(ISI\) is a matrix with entries \(s_{ij}\) defined as follows [28,29]: \begin{equation*} s_{ij}=\left\{ \begin{array}{c} \frac{d_{i}d_{j}}{d_{i}+d_{j}}\text{, &nbsp&nbsp }ij\in E(G) \\ 0\text{, &nbsp&nbsp&nbsp Otherwise} \end{array} \right.. \end{equation*} Let \(s_{1}\geq s_{2}\geq …\geq s_{n}\) be the eigenvalues of the matrix \( ISI \). It is elementary to show that where \(tr(ISI)\) is traces of \(ISI\) [28,29]. The energy of the \(ISI\) adjacency matrix is defined in [28,29] as

Lemma 1. [30,31] Let \(A\), \(B\) be Hermitian matrices of order \(n\). Suppose that \(A,B\) and \(A+B\) be \(\lambda _{i}(A),\lambda _{i}(B)\) and \(\lambda _{i}(A+B)\) for \( i=1,2,…,n\), rexpectively, each algebraically ordered in nonincreasing order. Then, for \(i=1,2,…,k,\) \begin{equation*} \lambda _{i}(A)+\lambda _{n}(B)\leq \lambda _{i}(A+B)\leq \lambda _{i}(A)+\lambda _{1}(B). \end{equation*}

Vukicevic et al., found that the ISI index is an important estimator of the total surface area of octane isomers [27]. Sedlar et al., obtained extremal values for ISI index of various graph classes [32]. Lokesha et al., studied on the ISI index of some nanostructure [33]. Nezhad et al., presented the ISI index of some nanotubes [34]. Chen and Deng gave some bounds for the ISI index in terms of various graph parameters [35]. Hafeez and Farooq studied on \(ISI\) energy formula of several graph classes [36].

In this study, we computed the \(ISI \) energies, spectral radii of ISI matrices, and the ISI indices of the molecular graph of the HA-PTX conjugates. Furthermore, we compared the inverse sum indeg indices and the inverse sum indeg energies for the molecular graph of the HA-PTX conjugates used in anticancer drug production.

2. The inverse sum indeg index (\(ISI\)), \(ISI\) energy, spectral radius of molecular graph of the Hyaluronic Acid-Paclitaxel conjugates

Let \(G\) be molecular graph of HA-PTX conjugate with \(n\). Then, \( |V(G_{n})|=87n\) and \(|E(G_{n})|=96n-1\) ([8,13,14]).

Theorem 1. Let \(G\) be molecular graph of HA-PTX conjugate with \(n=1\) unit. Then, \begin{equation*} ISI(G)=\frac{6697}{60}. \end{equation*}

Proof. As discussed in [8,13,14], the edge set of \(G\) can be partitions as follows:

\(\left\vert E_{1,2}\right\vert=\left\vert\{d_{u}=1\text{ and }d_{v}=2 \}\right\vert=1,\)

\(\left\vert E_{1,3}\right\vert=\left\vert\{d_{u}=1\text{ and }d_{v}=3 \}\right\vert=17\),

\(\left\vert E_{1,4}\right\vert=\left\vert\{d_{u}=1\text{ and }d_{v}=4 \}\right\vert=4\),

\(\left\vert E_{2,2}\right\vert=\left\vert\{d_{u}=2\text{ and }d_{v}=2 \}\right\vert=14\),

\(\left\vert E_{2,3}\right\vert=\left\vert\{d_{u}=2\text{ and }d_{v}=3\}\right\vert=30\),

\(\left\vert E_{2,4}\right\vert=\left\vert\{d_{u}=2\text{ and }d_{v}=4 \}\right\vert=3\),

\(\left\vert E_{3,3}\right\vert=\left\vert\{d_{u}=3\text{ and }d_{v}=3 \}\right\vert=18\),

\(\left\vert E_{3,4}\right\vert=\left\vert\{d_{u}=3\text{ and }d_{v}=4 \}\right\vert=7\),

\(\left\vert E_{4,4}\right\vert =\left\vert\{d_{u}=4\text{ and }d_{v}=4 \}\right\vert=1\).

Assume that \(\gamma _{uv}=\) \(\frac{d_{u}d_{v}}{d_{u}+d_{v}}\). From Equation (1), it can be written From Equation (4), we obtain \begin{equation} ISI(G)=1\times \frac{2}{3}+17\times \frac{3}{4}+4\times \frac{4}{5}+14\times \frac{4}{4}+30\times \frac{6}{5}+3\times \frac{8}{6}+18\times \frac{9}{6} +7\times \frac{12}{7}+1\times \frac{16}{8}. \notag \end{equation}

Theorem 2. Let \(G\) be molecular graph of HA-PTX conjugate with \(n=1\) unit. Then, \(s_{1}(G)=7.2712\).

Proof. The eigenvalues of the inverse sum indeg matrix of the molecular graph of the HA-PTX conjugate with \(n=1\) are calculated using the MATLAB program. The positive eigenvalues are: \(7.2712,\,4.0449,\,3.5368,\,3.2252,\,3.0890,\, 3.0072,\,2.9687,\) \(2.6823,\,2.5252,\,2.3681,\,2.2741,\,2.1448,\,2.0263,\,1.8462,\) \(1.7983,\,1.7280,\,1.6222,\,1.6016,\,1.5699,\, 1.4821,\,1.4599,\,\) \(1.2686,\) \(1.1608,\,1.0529,\,1,\,1,\,1,\, 0.9905,\,0.8327,\,0.8027,\,\) \(0.6178,\,0.4489,\,0.3813,\,0.3580,\,0.2976,\, 0.2290,\,0.2128,\,\) \(0.1792,0.1264.\) The spectral radius of and the smallest eigenvalue of the inverse sum indeg matrix of the HA-PTX conjugate with \(n=1\) are \(7.2712,-7.2712,\) respectively.

Theorem 3. Let \(EISI(G)\) be the inverse sum energy of the molecular graph of HA-PTX[1]. Then, \begin{equation*} EISI(G)=132.4624. \end{equation*}

Proof. From Equation (2), it can be written \(EISI=2\underset{i=1}{\sum }s_{i}\) for \(s_{i}>0.\) The proof is complemented from the positive eigenvalues of the inverse sum indeg matrix of HA-PTX conjugate with \(n=1\) in the proof of Theorem 2 and Equation (3).

Theorem 4. If \(G\) is the molecular graph of HA-PTX[n] then \begin{equation*} ISI(G)=\frac{3413}{30}n-\frac{43}{20}. \end{equation*}

Proof. Assume that \(G\) is the molecular graph of HA-PTX[n]. As discussed in [13] , the edge set of \(G\) can be partitioned as;

\(\left\vert E_{1,2}\right\vert=\left\vert\{d_{u}=1\text{ , }d_{v}=2 \}\right\vert=n,\)

\(\left\vert E_{1,3}\right\vert=\left\vert\{d_{u}=1\text{ , }d_{v}=3 \}\right\vert=16n+1\),

\(\left\vert E_{1,4}\right\vert=\left\vert\{d_{u}=1\text{ , }d_{v}=4 \}\right\vert=4n\),

\(\left\vert E_{2,2}\right\vert=\left\vert\{d_{u}=2\text{ , }d_{v}=2 \}\right\vert=13n+1\),

\(\left\vert E_{2,3}\right\vert=\left\vert\{d_{u}=2\text{ , }d_{v}=3 \}\right\vert=32n-2\),

\(\left\vert E_{2,4}\right\vert=\left\vert\{d_{u}=2\text{ , }d_{v}=4 \}\right\vert=3n\),

\(\left\vert E_{3,3}\right\vert=\left\vert\{d_{u}=3\text{ , }d_{v}=3 \}\right\vert=19n-1\),

\(\left\vert E_{3,4}\right\vert=\left\vert\{d_{u}=3\text{ , }d_{v}=4 \}\right\vert=7n\),

\(\left\vert E_{4,4}\right\vert=\left\vert\{d_{u}=4\text{ , }d_{v}=4 \}\right\vert=n\).

Assume that \(\gamma _{uv}=\) \(\frac{d_{u}d_{v}}{d_{u}+d_{v}}\). From Equation (4), the following equation is obtained \begin{align*} ISI(G) =&n\times \frac{2}{3}+\left( 16n+1\right) \times \frac{3}{4} +4n\times \frac{4}{5}+\left( 13n+1\right) \times \frac{4}{4}+\left( 32n-2\right) \times \frac{6}{5}+3n\times \frac{8}{6} \\ &+\left( 19n-1\right) \times \frac{9}{6}+7n\times \frac{12}{7}+n\times \frac{16}{8}. \end{align*} This proof is completed by the calculation.

Theorem 5. If \(G\) is the molecular graph of HA-PTX[n], then \begin{equation*} 5.9455\leq s_{1}(G)\leq 8.5969. \end{equation*}

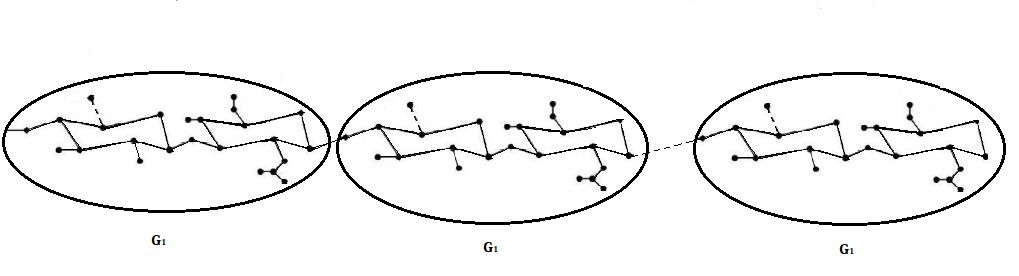
Proof. Suppose that \(G_{1}\) and \(G\) are the molecular structures of HA-PTX conjugate with \(n=1\) and HA-PTX[n], respectively. Let \(ISI^{^{\prime }}\) be the \(ISI\) matrix of \(G_{1} \) which is \(87\times 87\) matrix. Let \(ISI\) be the \(ISI\) matrix of \(G\). Figure 3 shows the bridge graph of the molecule of HA-PTX conjugates with \(n=1\).

By using Figure 3, it can be written the \(ISI\) matrix of \(G\) is as follows where \begin{equation*} A_{87n\times 87n}= \begin{bmatrix} ISI^{^{\prime }} & \ast & … & \ast \\ \ast & ISI^{^{\prime }} & … & \ast \\ \ast & \ast & … & \ast \\ \ast & \ast & … & \ast \\ \ast & \ast & … & ISI^{^{\prime }} \end{bmatrix} _{87n\times 87n}, \end{equation*} where \(\ast \) is \(0_{87\times 87}\) and \begin{equation*} B_{87n\times 87n}= \begin{bmatrix} 0_{84\times 84} & 0_{84\times 5} & 0_{84\times 82} & 0_{84\times 5} & 0_{84\times 82} & & 0_{84\times 82} & 0_{84\times 5} & 0_{84\times 85} \\ 0_{5\times 84} & C & 0_{5\times 82} & 0_{5\times 5} & 0_{5\times 82} & & 0_{5\times 82} & 0_{5\times 5} & 0_{5\times 85} \\ 0_{82\times 84} & 0_{82\times 5} & 0_{82\times 82} & 0_{82\times 5} & 0_{82\times 82} & & 0_{82\times 82} & 0_{82\times 5} & 0_{82\times 85} \\ 0_{5\times 84} & 0_{5\times 5} & 0_{5\times 82} & C & 0_{5\times 82} & & 0_{5\times 82} & 0_{5\times 5} & 0_{5\times 85} \\ 0_{82\times 84} & 0_{82\times 5} & 0_{82\times 82} & 0_{82\times 5} & 0_{82\times 82} & … & 0_{82\times 82} & 0_{82\times 5} & 0_{82\times 85} \\ \vdots & & & & & … & & & \\ 0_{82\times 84} & 0_{82\times 5} & 0_{82\times 82} & 0_{82\times 5} & 0_{82\times 82} & & 0_{82\times 82} & 0_{82\times 5} & 0_{82\times 85} \\ 0_{5\times 84} & 0_{5\times 5} & 0_{5\times 82} & 0_{5\times 5} & 0_{5\times 82} & & 0_{5\times 82} & C & 0_{5\times 85} \\ 0_{85\times 84} & 0_{85\times 5} & 0_{85\times 82} & 0_{85\times 5} & 0_{85\times 82} & & 0_{85\times 82} & 0_{85\times 5} & 0_{85\times 85} \end{bmatrix} _{87n\times 87n}, \end{equation*} and \begin{equation*} C= \begin{bmatrix} 0 & 1/5 & 0 & 0 & 0 \\ 1/5 & 0 & 3/10 & 6/5 & 0 \\ 0 & 3/10 & 0 & 0 & 0 \\ 0 & 6/5 & 0 & 0 & 9/20 \\ 0 & 0 & 0 & 9/20 & 0 \end{bmatrix} _{5\times 5}. \end{equation*} By using the Matlab program, the eigenvalues of the \(C\) matrix are So, the \(B\) matrix has \(n-1\) eigenvalues each \(-1.3257\), \(-0.1224\), \(0.1224\) and \(1.3257\). Other eigenvalues of the \(B\) matrix are \(0\). The \(A_{87n\times 87n}\) matrix has \(n\) eigenvalues each the eigenvalues in the proof of Theorem 2. From Theorem 2, the eigenvalues in (6) and Lemma 1 , we have \begin{equation*} 7.2712+(-1.3257)\leq s_{1}(G)\leq 7.2712+1.3257. \end{equation*}

Theorem 6. If \(G\) is the molecular graph HA-PTX[n], then \begin{equation*} -6.7919n\leq EISI(G)\leq 223.8799n. \end{equation*}

Proof. From the eigenvalues in (6), it is known that the smallest eigenvalue of the \(B\) matrix is \(-1.3257\) and spectral radius of the \(B\) matrix is \( 1.3257\). By using the eigenvalues from the proof of Theorem 2 and Lemma 1, one can obtain the eigenvalues of graph \(G\) for \(i=1,…87.\) \begin{equation*} s_{i}(A)+s_{87n}(B)\leq s_{i}(ISI(G))\leq s_{i}(A)+s_{1}(B). \end{equation*} From the above inequality, \(s_{i}(ISI(G))\) is negative for all eigenvalues between \((-7.2712)\)-\((-1.4599)\) of the matrix \(A\). So, the following inequality is obtained from Equation (3) \begin{align*} 2[7.2712+…+1.4599]+\overset{87}{\underset{i=1}{\sum }}s_{87n}(B) \leq & \overset{87}{\underset{i=1}{\sum }}s_{i}(ISI(G))\leq 2[7.2712+…+1.4599]+ \overset{87}{\underset{i=1}{\sum }}s_{1}(B) \\ 108.544-115.3359 \leq &\overset{87}{\underset{i=1}{\sum }}s_{i}(ISI(G))\leq 108.544+115.3359 \\ -6.7919 \leq &\overset{87}{\underset{i=1}{\sum }}s_{i}(ISI(G))\leq 223.8799. \end{align*} Since the \(A\) matrix has \(n\) eigenvalues in the proof of Theorem 2 , this proof is completed.

3. Comparison with the inverse sum indeg index, spectral radius and ISI energy of molecular graphs of Hyaluronic Acidpaclitaxel conjugates

Table 1 shows spectral radii, the inverse sum indeg indices and the ISI energies of molecular graphs of Hyaluronic Acid-Paclitaxel (HA-PTX) conjugates with \(n=1,2,3,4,5\). The eigenvalues of molecular graphs of HA-PTX conjugates with \(n=2,3,4,5\) are computed by the Matlab program and the results are given in Table 2, Table 3, Table 4 and Table 5, respectively, in the appendix.

Table 1.The spectral radii, the inverse sum indeg indices and the ISI energies of Hyaluronic Acid-Paclitaxel conjugates with \(n=1,2,3,4,5\).

\(G\)	\(s_{1}\)	\(ISI(G)\)	\(EISI(G)\)
\(n=1\)	\(7.2712\)	\(111.6166\)	\(132.4624\)
\(n=2\)	\(7.2712\)	\(225.3833\)	\(263.1968\)
\(n=3\)	\(7.2712\)	\(339.15\)	\(395.397\)
\(n=4\)	\(7.2712\)	\(452.9166\)	\(535.8942\)
\(n=5\)	\(7.2712\)	\(566.6833\)	\(667.5636\)

The graphical representation of these results was obtained with the Microsoft office excel program. Figure 4 shows a diagram of the data of Table 1. It seems that the inverse sum indeg index from the data of Table 1 and Theorem 3 is an asymptotic line. An interval for the energy is obtained in Theorem 5 when the eigenvalues for the \(EISI \) value of the Hyaluronic Acid-Paclitaxel conjugates are difficult to calculate as \(n\) units increased. From this interval and the data in Table 1, we conjecture that the energy probably will be tended to line, asymptotically. Our calculations suggest that the inverse sum indeg energy of the Hyaluronic Acid-Paclitaxel conjugates can be evaluated by \(EISI(G)=139.29n-3.9671 \) from Table 1. It was found that the inverse indeg energy and \(ISI\) index of the Hyaluronic Acid-Paclitaxel conjugates increase with increasing of \(n\) unit.

4. Conclusion

Studying the physicochemical properties of a molecule or molecular compound is not only time consuming but also a costly process. Therefore, mathematical chemistry focuses on topological indices. As the number of vertices of a molecular graph increases, it is difficult to obtain data and make calculations on it. In this case, computational and statistical methods become important for analyzing the behavior of the data. In this way, the desired values can become predictable without time-consuming experiments.

HA-PTX conjugates are popular lately, especially in drug manufacturing. Therefore, it has been considered necessary to calculate the topological indices of their molecular graphs in order to examine the physicochemical and biological properties of these molecules. This study mainly aims to compare the eigenvalue-based energy of HA-PTX conjugates in the light of molecular structural analysis with the degree-based index. The ISI index and ISI energy of molecular structures of HA-PTX conjugates are determined and compared. This study gives information about the energy levels of electrons and the strength of particles of the Hyaluronic Acid-paclitaxel conjugates. The results obtained in this study are thought to contribute to the applications in chemistry and pharmaceutical science in cancer treatment.

5. Appendix

The eigenvalues of HA-PTX conjugates with \(n=2,3,4,5\) are computed by the Matlab program and the results are given in Table 2, Table 3, Table 4 and Table 5, respectively.

Table 2. The positive eigenvalues of HA-PTX conjugates with \(n=2.\).

\(7.2712\), \(7.2712\),\(4.0449\), 4.0449, 3.5368, 3.5368, 3.3203, 3.2340, 3.1426,3.0898,
3.0384, 3.0148, 2.9687, 2.9688, 2.6823, 2.6823, 2.5252, 2.5252, 2.3740,2.3682,
2.3034, 2.2737, 2.2207, 2.1453, 2.0642, 2.0282, 1.9172, 1.8465,1.8384,1.7997,
1.7283, 1.7280, 1.6224, 1.6222, 1.6179, 1.1615, 1.6016, 1.6016, 1.1605,1.5699,
1.5699, 1.4813, 1.4667, 1.4599, 1.4310, 1.2676, 1.0594, 1.0524, 1, 1, 1, 1,1, 1,
0.9907, 0.9905, 0.8445, 0.8337, 0.8064, 0.8015, 0.6180, 0.6178, 0.4917,0.4467,
0.3976, 0.3781, 0.3583, 0.3579, 0.3138, 0.2971, 0.2926, 0.2290, 0.2129,0.2128,
0.1792, 0.1792, 0.1272, 0.1264, 0.0784

Table 3. The positive eigenvalues of HA-PTX conjugates with \(n=3 \).

\(7.2712\), \(7.2712\), \(7.2712\), \(4.0449\), \(4.0449\), \(4.0449\), \(3.5368\), \( 3.5368 \), \(3.5368\), \(3.3303\),
\(3.2944\), \(3.2351\), \(3.1612\), \(3.1255\), \(3.0897\), \(3.0481\), \(3.0286\), \(3.0154\), 2.9688, 2.9688,
2.9687, 2.6823, 2.6823, 2.6823, 2.3796, 2.3705, 2.3683, 2.3126, 2.2738,2.2914,
2.5252, 2.5252, 2.5252, 2.2207, 2.1869, 2.1447, 2.0888, 2.0474, 2.0280,1.9370,
1.8991, 1.8466, 1.8391, 1.8378, 1.8002, 1.7285, 1.7283, 1.7280, 1.6823,1.6222,
1.6222, 1.6222, 1.6016, 1.6016, 1.6016, 1.5792, 1.5699, 1.5699,1.5699,1.4813,
1.4668, 1.4666, 1.4599, \(1.4318+0.0034i\), 1.4318-0.0034i, 1.1618,1.1610,1.1605,
1.2676, 1.0524, 1.0613, 1.0569, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0.9908, 0.9907,0.9905,
0.8488, 0.8400, 0.8353, 0.8084, 0.8047, 0.8015, 0.6181, 0.6180, 0.6178,0.5062,
0.4768, 0.4466, 0.4011, 0.3926, 0.3780, 0.3584, 0.3582, 0.3579, 0.3208,0.3067,
0.2971, 0.2936, 0.2912, 0.2290, 0.2129, 0.2129,0.2128, 0.1792, 0.1792,0.1792,
0.1273, 0.1271, 0.1264, 0.0796, 0.0764

Table 4. The positive eigenvalues of HA-PTX conjugates with \(n=4.\) .

\(7.2712\), \(7.2712\), \(7.2712\), \(7.2712\), \(4.0449\), \(4.0449\), \(4.0449\), \( 4.0449 \), \(3.5368\), \(3.5368\),
\(3.5368\), \(3.5368\), \(3.3422\), \(3.3237\), \(3.2818\), \(3.2364\), \(3.1881\), \(3.1473\), \(3.1200 \), \(3.0899\),
\(3.0515 \), \(3.0406\), \(3.0242\), \(3.0176\), \(2.9688\), \(2.9688\), \(2.9687\), \( 2.9687\), \(2.6823\), \(2.6823 \),
\(2.6823\), \(2.6823\), \(2.5252\), \(2.5252 \), \(2.5252\), \(2.5252\), \(2.3833\), \( 2.3747\), \(2.3695\), \(2.3684\),
\(2.3172\), \(2.3042\), \(2.2878\), \(2.2738\), \(2.2207\), \(2.2160\), \(2.1868 \), \( 2.1453\), \(2.0981\), \(2.0660\),
\(2.0403\), \(2.0284\), \(1.9415\), \(1.9216\), \(1.8852\), \(1.8467\), \(1.8392\), \(1.8388\), \(1.8371\), \(1.8013 \),
\(1.7294\), \(1.7283\), \(1.7283\), \(1.7280\), \(1.7155\), \(1.6249\), \(1.6222\), \(1.6222\), \(1.6222\), \(1.6217\),
\(1.6016\), \(1.6016\), \(1.6016 \), \(1.6016\), \(1.5699\), \(1.5699\), \(1.5699\), \( 1.5699\), \(1.5664\), \(1.4813\),
\(1.4674\), \(1.4668\), \(1.4666\), \(1.4599\), \(1.4426\), \(1.4295+0.0034i\), \( 1.4295-0.0034i\),
\(1.2683\), \(1.1620\),\(1.1615\), \(1.1608\), \(1.1605\), \(1.0626\), \(1.0598\), \(1.0563\) , \(1.0524\), \(1\), \(1\), \(1\),
\(1\), \(1\), \(1\), \(1\), \(1\), \(1\), \(1\), \(1\), \(1\), \(0.9908\), \(0.9907\), \(0.9906\), \( 0.9905\), \(0.8493\), \(0.8449\), \(0.8380\),
\(0.8350\), \(0.8096 \), \(0.8064\), \(0.8036\), \(0.8015\), \(0.6182\), \(0.6178\), \( 0.6180\), \(0.6180\), \(0.5113\),
\(0.4908\), \(0.4706\), \(0.4466\), \(0.4018\), \(0.3974 \), \(0.3896\), \(0.3779\), \( 0.3584\), \(0.3583\), \(0.3582\),
\(0.3579\),\(0.3230\), \(0.3125\), \(0.3040\), \(0.2970\), \(0.2940\), \(0.2920\), \(0.2907\), \(0.2290\), \(0.2129\),
\(0.2129\), \(0.2129\), \(0.2128\), \(0.1792\), \(0.1792\), \(0.1792\), \(0.1792\), \(0.1273\), \(0.1272\), \(0.1271\),
\(0.1264 \), \(0.0797\), \(0.0770\), \(0.0755\)

Table 1. The positive eigenvalues of HA-PTX conjugates with \(n=5.\)

\(7.2712\), \(7.2712\), \(7.2712\), \(7.2712\), \(7.2712\), \(4.0449\), \(4.0449\), \( 4.0449 \), \(4.0449\), \(4.0449\),
\(3.5368\), \(3.5368\), \(3.5368\), \(3.5368\), \(3.5368\), \(3.3505\), \(3.3305\), \(3.3141\), \(3.2759\), \(3.2373 \),
\(3.2040\), \(3.1608\), \(3.1404\), \(3.1190\), \(3.0899\), \(3.0527\), \(3.0464\), \(3.0362\), \(3.0222\), \(3.0185\),
\(2.9687\), \(2.9687 \), \(2.9688\), \(2.9688\), \(2.9688\), \(2.6823\), \(2.6823\), \( 2.6823\), \(2.6823\), \(2.6823\),
\(2.3859\), \(2.3780\), \(2.3722\), \(2.3684 \), \(2.3691\), \(2.3203\), \(2.3103\), \( 2.2738\), \(2.2971\), \(2.2864\),
\(2.2207\), \(2.5252\), \(2.5252\), \(2.5252\), \(2.5252\), \(2.5252 \), \(2.2158\), \( 2.2161\), \(2.1868\), \(2.1453\),
\(2.1011\), \(2.0804\),\(2.0556\), \(2.0366\), \(2.0287\), \(1.9428\), \(1.9324\), \(1.9106\) , \(1.8749\), \(1.8468\),
\(1.8392\), \(1.8390\), \(1.8384\), \(1.8361\), \(1.8021\), \(1.7377\), \(1.7284\), \(1.7283\), \(1.7283\), \(1.7280 \),
\(1.7264\), \(1.6591\), \(1.6222\), \(1.6222\), \(1.6222\), \(1.6222\), \(1.6221\), \(1.6016\), \(1.6016\), \(1.6016\),
\(1.6016\), \(1.6016 \), \(1.5979\), \(1.5699\), \(1.5699\), \(1.5699,\) \(1.5699\), \( 1.5699\), \(1.5610\), \(1.4813\),
\(1.4675\), \(1.4673\), \(1.4668\), \(1.4666 \), \(1.4599\), \(1.4450\), \(1.4375\),1.4290+0.0028i,
1.4290-0.0028i,1.2683,1.1623,1.1617,1.1612,1.1608,1.1605,1.0637, \(1.0610\),\( 1.0585\),
\(1.0561\),\(1.0524\),\(1,1,1,1,1,1,1,1,\) 1,1,1,1,1,1,1, 0.9908,0.9908, 0.9907,\( 0.9906\),
\(0.9905\),0.8495,0.8470,0.8419,0.8371,0.8347,0.8104,0.8075,0.8051,0.8031,0.8015,
0.6182, 0.6181 , \(0.6180\), \(0.6179\), \(0.6178\), \(0.5138\), \(0.4996\), \(0.4814\),\(0.4677\), \(0.4466 \),
\(0.4021\), \(0.3995\), \(0.3944\), \(0.3878\), \(0.3779\), \(0.3584\), \(0.3584\), \(0.3583\), \(0.3581\), \(0.3579\),
\(0.3239\), \(0.3165 \), \(0.3084\), \(0.3025\), \(0.2970\), \(0.2943\), 0.2927, 0.2913,0.2906, 0.2290,
0.2129, 0.2129, 0.2129, 0.2129, 0.2128, 0.1792, 0.1792, 0.1792, 0.1792,0.1792,
0.1273, 0.1272, 0.1271, 0.1270, 0.1264, 0.0797, 0.0774, 0.0763, 0.0749

Conflicts of Interest

The author declares no conflict of interest.

Acknowledgments

The author is deeply thankful to the editor and the reviewers for their valuable suggestions to improve the quality of this manuscript.