Sombor indices – back to geometry

1. Introduction

In this paper, we are concerned with a geometric interpretation of vertex-degree-based topological indices, extending the considerations from Ref. [1]. Let \(G\) be a simple graph with vertex set \(\mathbf V(G)=\{v_1,v_2,\ldots,v_n\}\) and edge set \(\mathbf E(G)\). The degree (= number of first neighbors) of the vertex \(v_i \in \mathbf V(G)\) will be denoted by \(d_i\). If the vertices \(v_i\) and \(v_j\) are adjacent, then the edge connecting them is labeled by \(ij\).

In the mathematical and chemical literature, several dozens of vertex-degree-based (VDB) graph invariants (usually referred to as ”topological indices”) have been introduced and extensively studied [1,2,3,4]. Their general formula is

where \(F(x,y)\) is some function with the property \(F(x,y)=F(y,x)\).

Some of these VDB indices, mentioned in the later part of the paper, are the first and second Zagreb index [5,6]

the Albertson index [7] and the Sombor index [1] In [1], the ordered pair \((a,b)\), where \(a=d_i\), \(b=d_j\), \(a \geq b\), is called the degree-coordinate of the edge \(ij \in \mathbf E(G)\), and represented by a degree-point in a two-dimensional coordinate system, see Figure 1. The point with coordinates \((b,a)\) is then referred to as the dual-degree-point pertaining to the edge \(ij\).

The distance between the degree-point of the edge \(ij\) (denoted by \(A\) in Figure 1), and the origin (\(O\)), assuming an Euclidean metrics, is \(\sqrt{d_i^2+d_j^2}\). Summing this over all edges of the graph \(G\), one obtains the right-hand side of Eq. (4), i.e., the Sombor index [1].

We indicate this transformation as

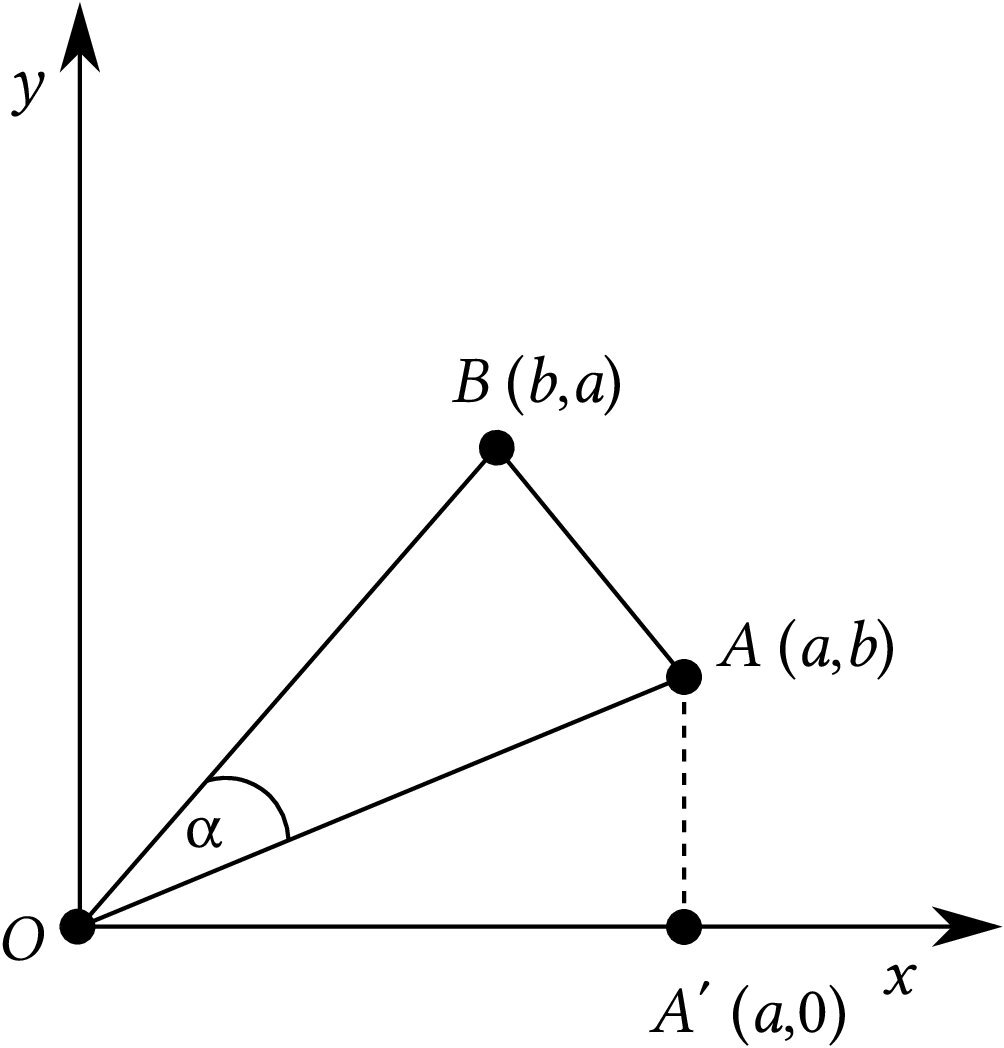
In fact, the Sombor index was actually conceived by using the above geometric considerations [1]. This VDB topological index soon attracted much attention, and its numerous mathematical [8,9,10,11,12,13,14] and chemical [15,16,17,18,19] applications have been established. Yet, with a single exception [20], the geometry-based features of the Sombor index were ignored, and only its algebraic and combinatorial aspects were in focus of interest.

In this paper we intend to point out the great variety of Sombor-index-like VDB graph invariants that can be constructed by means of geometric arguments.

First of all, we recall that in [1], it was shown that the distance between the degree-point and its dual (points \(A\) and \(B\) in Figure 1), is equal to \(\sqrt{2}\,\big|d_i-d_j \big|\), which after adding over all edges yields the Albertson index, i.e., \(\sqrt{2}\,Alb(G)\), cf. Eq. (3). In analogy to formula (5), we write this as:

Let \(A’\) be the projection of the point \(A\) on the \(x\)-axis, see Fig. 1. Consider the triangle \(AA’O\). Then, bearing in mind Eqs (2) and (4), we straightforwardly conclude that \[ \sum_{ij \in \mathbf E(G)} perim(AA’O) = \sum_{ij \in \mathbf E(G)} \left[ \sqrt{d_i^2+d_j^2} + d_i + d_j \right] = SO(G) + M_1(G)\,, \] and \[ \sum_{ij \in \mathbf E(G)} area(AA’O) = \sum_{ij \in \mathbf E(G)} \frac{1}{2}\,d_i\,d_j = \frac{1}{2}\,M_2(G)\,, \] where \(perim(X)\) and \(area(X)\) stand for the perimeter and area of the geometric object \(X\).

Thus, a few classical VDB topological indices have a geometry-based interpretation.

2. More Sombor-index-like graph invariants

In this section we consider the triangle formed by the degree-point, dual-degree-point, and the origin of the coordinate system, points \(A\), \(B\), and \(O\) in Figure 1. From this triangle, we generate a number of new Sombor-index-like VDB invariants, denoted below by \(SO_1,SO_2,\ldots,SO_6\).

First note that by bearing in mind Eqs. (5) and (6), we immediately get

\[ \sum_{ij \in \mathbf E(G)} perim(ABO) = 2\,SO(G) + \sqrt{2}\,Alb(G)\,. \] Using elementary geometry (Heron’s formula), knowing the distance between the points \(A\) and \(O\) (same as between \(B\) and \(O\)), cf. Eq. (5), as well as between \(A\) and \(B\), cf. Eq. (6), we obtain \[ area(ABO) = \frac{1}{2}\,\big(a^2-b^2 \big)\,, \] from which it follows \[ \sum_{ij \in \mathbf E(G)} area(ABO) = \sum_{ij \in \mathbf E(G)} \frac{1}{2}\,\big|d_i^2 – d_j^2 \big| := SO_1(G)\,. \] Let \(\alpha\) be the angle between the lines \(OA\) and \(OB\), see Figure 1. Using the classical formula \[ area(ABO) = \frac{1}{2}\,dist(OA)\,dist(OB)\,\sin \alpha\,, \] we get \[ \frac{1}{2}\,\big| d_i^2-d_j^2 \big| = \frac{1}{2}\,\left( \sqrt{d_i^2+d_j^2} \right)^2\,\sin \alpha \,,\] from which \[ \sum_{ij \in \mathbf E(G)} \sin \alpha = \sum_{ij \in \mathbf E(G)} \left| \frac{d_i^2 – d_j^2}{d_i^2+d_j^2} \right| := SO_2(G)\,. \] Denote by \(\Gamma_c\) the circumcircle (circumscribed circle) on the triangle \(ABO\). The respective incircle (inscribed circle) will be denoted by \(\Gamma_i\). Using elementary, yet somewhat lengthy, geometric reasoning, it can be shown that In connection with Eqs. (9) and (10), note that if the center of the incircle has coordinates \((\gamma,\gamma)\) and its distance from the origin is \(\sqrt{2}\,\gamma\), then \[ radius(\Gamma_i) = \frac{(a-b)\gamma}{\sqrt{a^2+b^2}} \hspace{10mm} \mbox{and} \hspace{10mm} radius(\Gamma_i) + \sqrt{2}\,\gamma = \frac{a+b}{\sqrt{2}}\,. \] The formulas (7)-(10) make it possible to introduce the following Sombor-index-like VDB invariants \begin{eqnarray*} SO_3(G) = \sum_{ij \in \mathbf E(G)} perim(\Gamma_c) & = & \sum_{ij \in \mathbf E(G)} \sqrt{2}\ \frac{d_i^2+d_j^2}{d_i+d_j}\,\pi \,,\\[3mm] SO_4(G) = \sum_{ij \in \mathbf E(G)} area(\Gamma_c) & = & \frac{1}{2} \sum_{ij \in \mathbf E(G)} \left( \frac{d_i^2+d_j^2}{d_i+d_j}\right)^2 \pi\,, \end{eqnarray*}\begin{eqnarray*} SO_5 = \sum_{ij \in \mathbf E(G)}perim(\Gamma_i) & = & \sum_{ij \in \mathbf E(G)} \frac{2\,|d_i^2-d_j^2|}{\sqrt{2} + 2\,\sqrt{d_i^2+d_j^2}}\,\pi \,,\\[3mm] SO_6 = \sum_{ij \in \mathbf E(G)} area(\Gamma_i) & = & \sum_{ij \in \mathbf E(G)} \left[ \frac{d_i^2-d_j^2} {\sqrt{2} + 2\,\sqrt{d_i^2+d_j^2}} \right]^2\! \pi\,. \end{eqnarray*} It would be interesting to examine the properties of these geometry-based topological indices, and see if these are usable in applications. What is immediately evident is that \(SO_1\), \(SO_2\), \(SO_5\), and \(SO_6\) are suitable for measuring graph irregularity [21], i.e., they are equal to zero if and only the underlying graph is regular.

Conflicts of Interest:

”The author declares no conflict of interest.”