We theoretically present the physical realization of one dimensional (1D) atom localization by superposition of three standing wave fields in a four-level tripod atomic configuration. The most interesting result that we observe is the variation of the bandwidth of the localization peaks with the intensity of the space independent Rabi frequency. A sharp single and double localized peaks are observed at different direction of the wave numbers. The bandwidth of a localized peak is reduced as the intensity of the space independent Rabi frequency goes on increasing, which corresponds to the reduction in the uncertainty. These results will hopefully contribute to the development of current high tech-applications.
The concept of atom localization comes from the birth of quantum mechanics. In 1927, Heisenberg [1] uses the uncertainty principal and suggests that an atom can be localized. Interest in the precise and accurate position measurement of atom is because of its rich potential application [2,3,4]. Atomic localization has a wide range of application, mostly in Bose-Einstein condensation [5], laser cooling and trapping [6], atom nano-lithography [7] and center of mass wave function [8].
The main phenomenon in the field of Quantum Optics and Laser Physics is the quantum interference and atomic coherence, by which giant Kerr nonlinearity [9], spontaneous emission enhancement [10], Optical bistability (OB) [11], electromagnetically induced transparency (EIT) [12,13] and many more aspects are obtained. For the localization of an atom in one dimension (1D) based on the atomic coherence and quantum interference, much efforts has been done. For example, Zubairy and his colleagues estimated numerous localization systems for a two-level system by resonant fluorescence [14,15]. Agarwal and kapale [16] obtained the atom localization in 1D by using the coherent population trapping (CPT) for three-level atomic scheme in a lambda-type. According to Agarwal scheme, the population measurement could localize the atom. This population had the same fringe pattern in one of the ground state as presented by Febry Perot interferometer. Storey et al., [17] and Marte and Zoller [18] introduced atomic localization passing through the standing wave regime. By using quantum interference, Kien et al., [19] showed the polarized atom localization in 1D. Paspalakis and Knight [20] used quantum interference for atom localization. Qamar et al., [21] used resonance fluorescence for atom localization. For 1D atomic localization through the internal state of atom and the field dual measurement [22], the driving field of amplitude control and phase [23], an atom can be localized. Nha et al., [24] explained the 1D atom localization inside the Ramsey interferometer arrangement by the interaction of quantized atom in nature with a standing-wave field. Sahrai et al., [25] proposed that the position measurement of an atom depends on absorption of a weak probe filed, due to which the probability of an atom localization is 50%. For more precise localization of an atom, Liu et al., [26] used the interference of double dark resonance which showed that the probability of finding atom is 50%. While Wang and jiang [27] detected 100% probability of atom localization by using coherent methodology. Recently, Proite et al., [28], by using the method of electromagnetically induced transparency (EIT), conducted an experiment in which the atomic level population was localized. They gained the result that population of accurate hyperfine level might be strongly localized than that of spatial period.
In this paper, a theoretical approach has been presented for the physical realization of the atom localization by superposition of three standing wave fields in a proposed four levels atomic configuration. The most interesting result that we encounter with, is the variation of the bandwidth of the localized peak with time independent Rabi frequency. It seems clear from our theoretical results that without disturbing the probability amplitude the bandwidths of the localized peaks are reduced as the intensity of the space independent Rabi frequency is increased and thus the reduction in the uncertainty can be achieved very easily. Though our approach is a theoretical one, but still our findings are very interesting and can actively support the day to day progress in the field of research and modern technology.
We also investigated that in the localization peaks, the space independent Rabi frequency condenses the uncertainty principal without disturbing the amplitude probability. In addition with the space independent wave fields, the width of the half maximum decreases. Along with this, it is investigated that the Doppler broadened effect and collision decay rate, which disturb the localization amplitude probability and the localization peaks, tends to doublet. When amplitude probability of the localized peaks changes, the collision decay rate is to be zero.
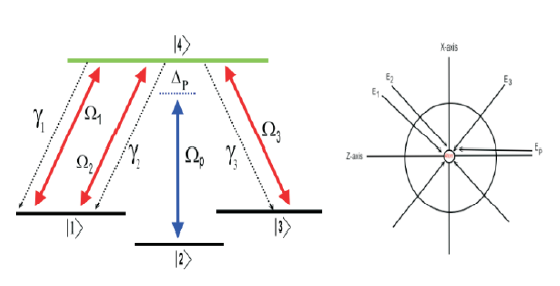
While the interaction Hamiltonian \(H_i\) is written as;
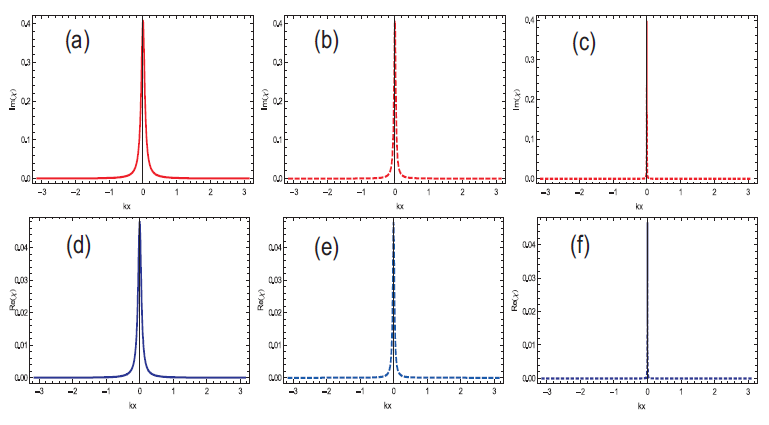
The atom field interaction through experimental and theoretical research led us to the new kinds of observations in physical phenomena. For the development of present technologies, a single atom in a trap, quantum lithography, localization of atom in the sub half wave length domain and quantum computing play important role. In Equation (8), we indicated the main result for precise and accurate position of the atom. The rate of decay \(\gamma\) is taken to be \(1GHz\). In atomic system, the universal physical constants are \(\hbar, \epsilon_0=1\). The real and imaginary parts of susceptibility are anticipated for the atom position at the range of \(-\pi< kx< \pi\). The position distribution functions \(Re(\chi)\) and \(Im(\chi)\) are related to the localization information of an atom. When the nodes and antinodes coincide, they form the stationary wave which appear on the real and imaginary distributed function of the probe field. The superposition of standing wave field expresses remarkable results for the development of localization peak in the space period of \(-\pi< kx< \pi\) with one wavelength domain, where \(\Omega\) shows the magnitude of space independent Rabi frequency i.e., \(|\Omega_1|=|\Omega_2|=|\Omega_3|=\Omega\).
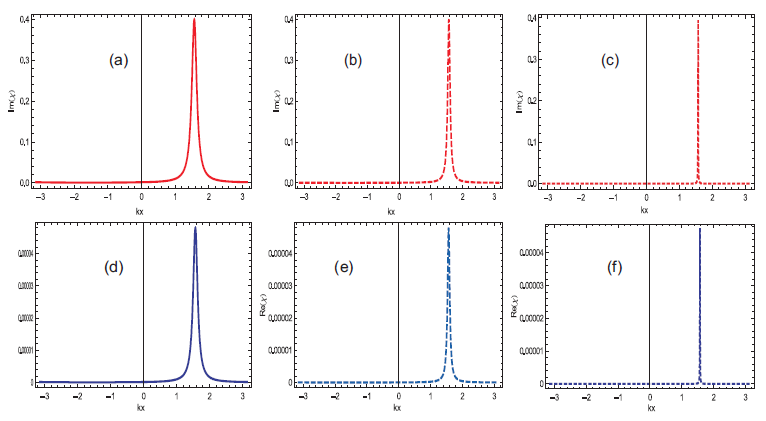
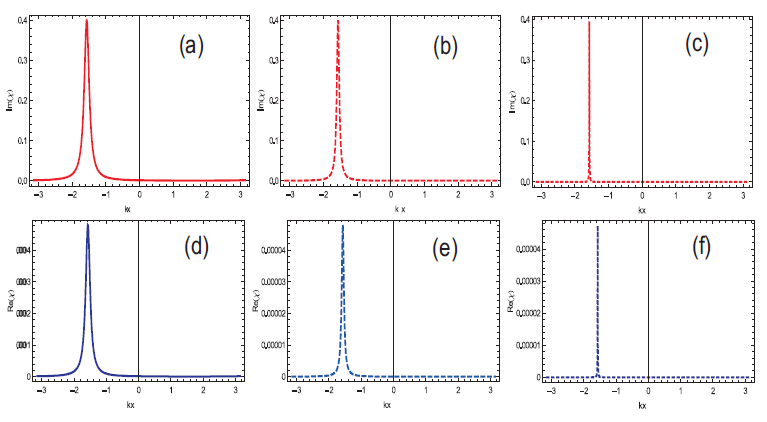
In this theoretical model, single localization peak is observed within position range of \(0< kx< \pm\pi\) or \(\lambda/2\) domain, where the phase are set to \(\pi/2, 3\pi/2\) with \(\eta_{1,3}=0.5\) and \(\eta_{2}=-0.5\). The probe detuning is taken \(\Delta_p=0\). Furthermore, when the strength of \(\Omega=|\Omega_{1,2,3}|\) increases the peak width becomes narrow and the uncertainty decreases. At a very high intensity, the peak bandwidth approaches to zero and minimum uncertainty is observed in the localized peaks as shown in Figures 2 and 3. When the phase is \(\pi/2\) then the single localized peak appears within the sub half wavelength domain \(-\pi< kx< 0\). If the phase is changed to \(3\pi/2\) then the single localized peak appears within sub half wavelength domain \(0< kx< \pi\) also with the change in phase from \(\pi/2\) to \(3\pi/2\) the position of single peak is shifted from left to right as shown in Figures 2 and 3. These results are applicable for the development of atomic nanolithography, trapping of neutral atoms, laser cooling, Bose-Einstein condensation and measurement of center of mass wave function.
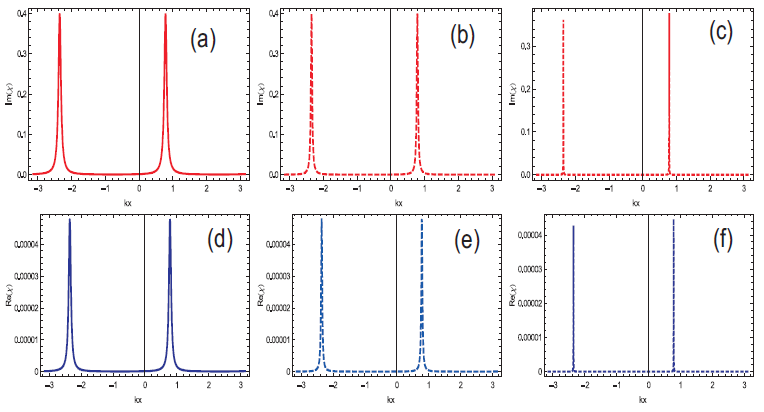
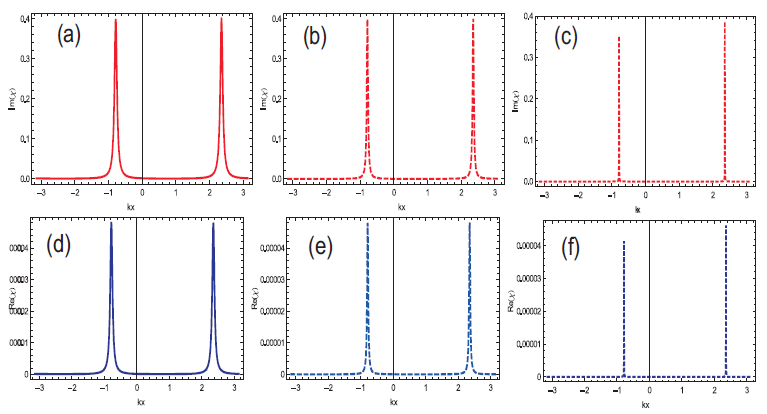
In Figures 4 and 5 the plots are traced for localization peaks of atom. It is observed that two localization peaks appear when the direction of wave numbers \(\eta_{1,2}=1\). In this case, one localization appear within the position range \(0< kx< \pi\) on the probe distributed function and other localized peak is within the position range \(-\pi< kx< 0\). The phase varies from \(\pi/2\) to \(3\pi/2\) as discussed in Figures 2 and 3 using both real and imaginary distribution function. It seems that one localized peak is near to the origin position (\(kx=0\)) and the other peak is away from the origin. The position of the localized peaks are shifted with the variation of phase \(\varphi\). The width of the localization peaks decreases with the strength of the space independent Rabi frequency \(\Omega\). Figure 6 shows the localized patron at the phase \(\varphi=\pi\) within position \(-\pi< kx< \pi\), where the detuning is \(\Delta_p=0\gamma\). In this case, a single peak appears at the position \(kx=0\) with \(40\%\) probability in the imaginary part of susceptibility.