Dynamics of Williamson fluid over an inclined surface subject to Coriolis and Lorentz forces

1. Introduction

An electrically conducting fluid moving in a magnetic field generates an electric current which induces a magnetic field and the magnetohydrodynamic force, known as Lorentz force, is built up in the flow [1]. Applications of magnetohydrodynamics flow can be found in jet printers, fusion reactors, and MHD generators. Most importantly is the study of heat and mass transfer in a magnetohydrodynamic flow which has practical applications in biosensors, aerosol generation and dispersion, and nuclear waste repository. Katagiri [2] studied the MHD Couette motion formation in a viscous incompressible fluid and found out that the velocity declines with increasing magnetic field strength. [3] presented an analysis of an unsteady MHD free convective HAMT in a boundary layer flow and found out that velocity profiles decrease with magnetic field, while concentration decreases with Schmidt number. Sheri and Modugula [4] analysed an unsteady MHD flow across an inclined plate and inferred that temperature profiles decrease with Prandtl number while velocity profiles increase with either the solutal Grashof number or thermal Grashof number. Sivaiah and Reddy [5] analysed HAMT of an unsteady MHD flow past a moving inclined porous plate. Flow velocity was found to rise with an increase in Magnetic field strength; as against the results from [2]. Their results showed that velocity profile increases with increasing solutal and thermal Grashof number; in agreement with the results from [2]. Also, velocity and concentration decrease with Schmidt number while temperature profile decreases with Prandtl number. Iva et al. [6] also supported the results of [2] across a rotating plane. Sreedhar and Reddy [7] considered the impact of chemical reaction in the presence of heat absorption and found out that velocity profiles decrease with both Prandtl number and magnetic field strength. Zafar et al. [8] analysed the effect of inclination angle on MHD flow. Hussain et al. [9] examined the magnetohydrodynamic flow of Maxwell nanofluid and deduced that flow velocity decreases as either magnetic field strength and/or inclination angle increases. The results also show that flow velocity increases as Maxwell parameter increases while flow temperature is enhanced with rising inclination angle.

Williamson fluid is a non-Newtonian fluid that exhibits shear thinning characteristics of non-Newtonian fluids. Williamson and Ouru [10,11] in 1929 experimentally introduced the Williamson fluid model which models a fluid whose viscosity reduces indefinitely as shear rate increases (meaning ” an infinite viscosity when there is no fluid motion but zero viscosity as the shear rate tend to infinity” ). In a study by Khan et al. [12], an extensive investigation is conducted to unravel the thermophysical properties of MHD Williamson flow past a simultaneously rotating and stretching surface. Results indicated that velocity is boosted as values of rotation gets larger and increment in \(Pr\) inhibits temperature distribution. Yusuf and Mabood [13] examined chemical reaction on MHD Williamson fluid flow over an inclined permeable wall. The results indicate that both the magnetic strength and the Williamson fluid parameter have an adverse effect on the fluid velocity. Srinivasulu and Goud [14] explored the impact of Lorentz force on Williamson’ s nanofluid. With a rise in magnetic strength, velocity profile diminishes but boosts the temperature and concentration profiles. The temperature and concentration profiles increase and velocity profile decreases with an increase in inclination angle. Li et al., [15] considers the heat generation and/or heat absorptions on MHD Williamson nanofluid flow.

Coriolis force is an inertia force that is generated in a rotating frame. It is the force responsible for the apparent curved trajectory of a linearly moving object in a rotating frame. The Coriolis force increases as the angular velocity of the rotating plane increases. Application of Coriolis force can be found in astrophysics, oceanography, and bioreactors [16,17]. The study of magnetohydrodynamic flow of Newtonian fluid over a rotating non-uniform surface was studied by [18]. It is found that simultaneously increasing the Coriolis force and Magnetic field strength leads to an increase in the flow temperature. Meanwhile, [19] extended the work of [18] by considering the non-Newtonian Casson fluid flow over a rotating non-uniform surface. The study showed that increasing Coriolis force increases the temperature profile and increases the primary velocity. A study of the flow of nanofluid flow over a rotating flat surface is conducted by [20]. It is recorded that the presence of Coriolis force has a significant impact on the arrangement of nanoparticles in the nanofluid.

Based on the available information, very little has not been done to figure out how Williamson fluid flows across an inclined plate. In this present study, a two-dimensional flow of Williamson flow past an inclined plate is considered. This study provides answers to the following questions; 1) what are the combined effects of Lorentz force and inclination angle on the magnetohydrodynamic flow of Williamson fluid over an inclined rotating plate? 2) what are the combined effects of Lorentz force and Coriolis force on the magnetohydrodynamic flow of Williamson fluid over an inclined rotating plate?

2. Governing equations

This study considers a steady boundary layer flow of a viscous, thermally and electrically-conducting Williamson fluid over an inclined porous plate that rotates at angular velocity \(\Omega.\) The plane is inclined at an angle \(\alpha\) and the flow configuration is shown in Figure 1.

The magnetic field is applied at an angle \(90^{o}\) to the direction of the flow with a constant magnetic field strength of \(B_{0}.\) The inclined surface is stretched linearly and the no-slip condition is upheld so that the velocity at the wall is the same as the velocity of the Williamson fluid layer closest to the wall. Hence, the velocity at the wall is given as \(u=ax.\) By including the porosity, Coriolis force and inclination angle in the formulations of [11], the system of governing equations comprising of the continuity equation, momentum equation, energy equation, and the species equation is given as

with the boundary conditions The quantities of industrial and engineering importance [4] are the coefficient of skin friction, Nusselt number and Sherwood number defined as \[ C_{f}=\frac{\nu}{a^{2}}\left(\frac{\partial u}{\partial y}\right)_{y=0},\;Nu=-\frac{x\left(\frac{\partial T}{\partial y}\right)_{y=0}}{\left(T_{w}-T_{\infty}\right)},\;Sh=-\frac{x\left(\frac{\partial C}{\partial y}\right)_{y=0}}{\left(C_{w}-C_{\infty}\right)}. \]

3. Methodology

By using the similarity variables \[ u=axf’,\;v=-\left(a\nu\right)^{\frac{1}{2}}f,\;\theta=\frac{T-T_{\infty}}{T_{w}-T_{\infty}},\ \Phi=\frac{C-C_{\infty}}{C_{w}-C_{\infty}},\;\eta=y\left(\frac{a}{\nu}\right)^{\frac{1}{2}}, \] the system of governing equations (Eqs. (1)-(4)) is transformed to the dimensionless form as with the dimensionless boundary conditions where the dimensionless parameters are the solutal and thermal Grashof number, Rotation parameter, magnetic field parameter, porosity parameter, Schmidt number, Brownian parameter, thermophoretic parameter, Prandtl number, and the Williamson fluid parameter defined as \begin{align*} & Gr_{t}=\frac{g\beta\left(T_{w}-T_{\infty}\right)}{a^{2}x},\;Gr_{s}=\frac{g\beta^{*}\left(C_{w}-C_{\infty}\right)}{a^{2}x},\;K=\frac{2\Omega}{a},M=\frac{\sigma B_{0}^{2}}{a\rho},\;K_{c}=\frac{\nu}{a\rho},\\ & Sc=\frac{\nu}{D_{B}},\;N_{b}=\frac{\tau D_{B}}{\alpha},\;N_{t}=\frac{\tau D_{T}\left(T_{w}-T_{\infty}\right)}{\alpha T_{\infty}},\;Pr=\frac{\nu}{\alpha},\;\gamma=\Gamma\left(\frac{2a^{3}x^{2}}{\nu}\right)^{\frac{1}{2}}\,. \end{align*} Also, the dimensionless form of the local skin friction \(C_{f},\) the Nusselt number \(Nu,\)and the Sherwood number \(Sh\) are \[ R_{e}^{\frac{1}{2}}C_{f}=2\left(1+\frac{\gamma}{2}f”\left(0\right)\right)f”\left(0\right),\;R_{e}^{-\frac{1}{2}}Nu=-\theta’\left(0\right),\;Re^{-\frac{1}{2}}Sh=-\Phi\left(0\right). \] Eqs. (6)-(8) can be written as a system of first order ordinary differential equations by using the transformations \[ X_{1}=f,\ X_{2}=f’,\ X_{3}=f”,\ X_{4}=\theta,\;X_{5}=\theta’,\ X_{6}=\Phi,\ X_{7}=\Phi’. \] Hence, the system is with the boundary conditions To solve the system (10), the boundary conditions (11) and (12) need to be converted to initial values. This can be achieved by using shooting technique which requires the choice \[ X_{1}\left(0\right)=0,\ X_{2}\left(0\right)=1,\ X_{3}\left(0\right)=s_{1},\ X_{4}\left(0\right)=0,\;X_{5}\left(0\right)=s_{2},\ X_{6}\left(0\right)=1,\ X_{7}\left(0\right)=s_{3}. \] By making repeated arbitrary assumptions for \(s_{1},s_{2}\) and \(s_{3},\) the problem is solved until the three remaining boundary conditions \[ X_{2}\left(\infty\right)\to0,\;X_{4}=1,\ X_{6}\left(\infty\right)=0. \] are satisfied. The problem is solved numerically using the MATLAB bvp4c solver (for other methods of solution, see [11]). The results from the present work is validated against the results of [22] in Table (1) with the choice of parameter values as \[ Gr_{t}=Gr_{s}=K_{c}=K=0,\alpha=\pi/2,M=N_{b}=N_{t}=Pr=0 \]

Table 1. Results validation for \(Re^{\frac{1}{2}}C_{f}\).

\(\gamma\)	0	0.1	0.2	0.3
Ahmed and Akbar \cite{22}	1.33930	1.29801	1.26310	1.22276
present study	1.33013	1.29880	1.26384	1.22345

4. Analysis and discussion of results

The resulting system (10) is solved using the MATLAB bvp4c solver and the solutions are presented in graphs and tables. The default values for the parameters are chosen as follows; \[ Gr_{t}=Gr_{s}=1.0,\;Sc=0.62,\;M=2,\;Pr=4,\;\alpha=\pi/6,\;K=N_{b}=N_{t}=K_{c}=\gamma=0.1. \] The results are analysed and discussed in this section.

4.1. Analysis of results

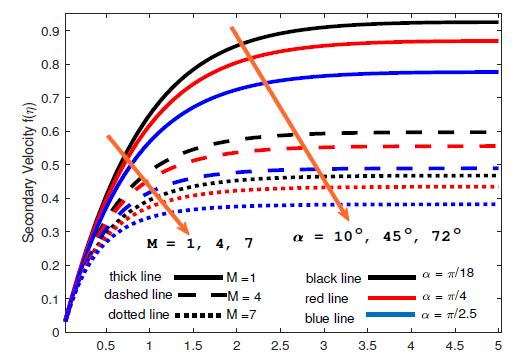
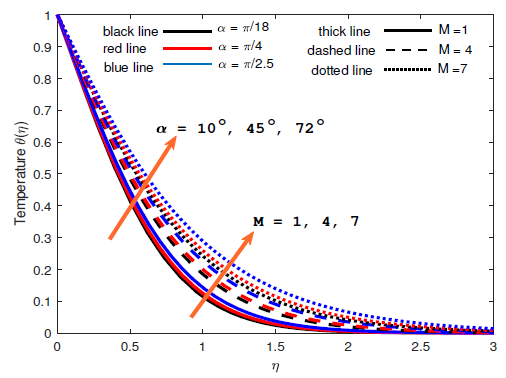
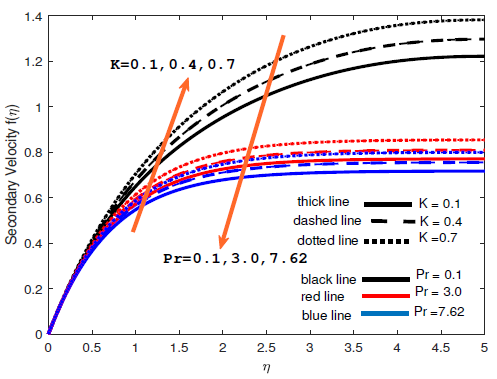
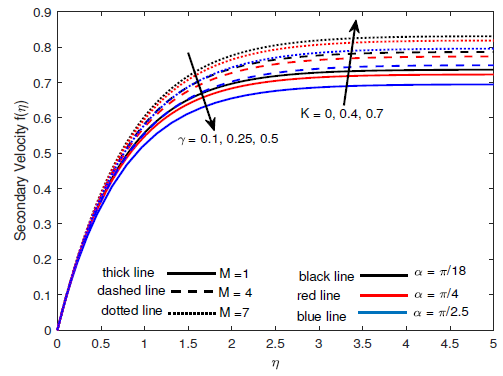
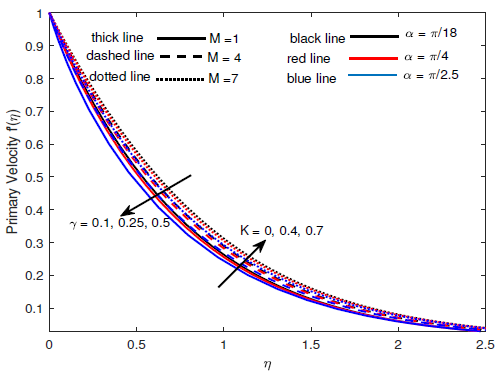
Figures 2 – 4 show the impact of simultaneously increasing the magnetic field strength and inclination angle on Williamson fluid flow over a rotating surface. Figures 2 and 3 show that the velocity reduces as magnetic field strength increases and inclination angle increases to \(90^{o}\) while the flow temperature increases as the magnetic field strength and inclination angle increase simultaneously as shown in Figure 4. The combined effects of rotation and Prandtl number on the velocity are shown in Figures 5 and 6. It is revealed that both the primary and secondary velocity profiles increase with increasing rotation, meanwhile, both the primary and secondary velocity profiles decrease with increasing Prandtl number. Figures 7 and 8 show the variations of velocity profiles with the simultaneous increase in Williamson fluid parameter and Coriolis force. The flow velocity profiles decrease in all directions with increasing Williamson fluid parameter but increase in all directions with increasing Coriolis force.

Tables 2 and 3 demonstrate how the rotation parameter and magnetic field strength affect the local skin friction, heat transfer rate and mass transfer rate. As rotation increases, the local skin friction decreases at the rate of -0.8052, the Nusselt number decreases at the rate 0.06 and Sherwood number increases at the rate 0.0218. On the other hand, the local skin friction increases at the rate of 0.7191, the Nusselt number decreases at the rate -0.0492 and Sherwood number decreases at the rate -0.016 as magnetic field strength increases. With this, it is evident that the local skin friction can be increased by increasing magnetic field strength and decreasing rotation. In addition, the rate at which heat is transferred can be improved by increasing rotation and reducing magnetic field strength. Finally, rate of convective mass transfer can be boosted by increasing rotation and reducing magnetic field strength.

Table 2. Quantities of interest with rotation parameter.

\(K\)	skin friction	Nusselt number	Sherwood number
0	2.70423	1.19702	1.23699
0.1	2.62641	1.20272	1.23899
0.2	2.54775	1.20851	1.24104
0.3	2.46822	1.21440	1.24315
0.4	2.38778	1.22039	1.24532
0.5	2.30637	1.22649	1.24755
0.6	2.22394	1.23270	1.24986
0.7	2.14044	1.23902	1.25224
slope	-0.80520	0.06000	0.02180

Table 3. Quantities of interest with magnetic field strength.

\(M\)	skin friction	Nusselt number	Sherwood number
1	1.22976	1.30996	1.28113
2	2.14044	1.23902	1.25224
3	2.93308	1.18045	1.23132
4	3.65485	1.13012	1.21514
5	4.32955	1.08584	1.20209
6	4.97109	1.04631	1.19122
7	5.58845	1.01062	1.18198
slope	0.71910	-0.04920	-0.01600

4.2. Discussion of results

The presence of a magnetic field generates the Lorentz force. The Lorentz force generated with the presence of magnetic field acts in the opposite direction to fluid flow and thereby causes a reduction in flow velocity. Increasing inclination angle reduces flow velocities in all directions since more work is done by the fluid to climb. Simultaneously increasing the magnetic field strength and inclination angle causes more reduction on flow velocity profiles in all directions. Meanwhile, heat energy is generated in the system as the Lorentz force opposes the motion (due to magnetic field presence) and more heat energy is also generated as the fluid climbs the plate (due to an increase in inclination angle). Hence, the temperature profile increases as both magnetic field strength and angle of inclination increase.

As the surface rotates, Coriolis force is generated. Hence, increasing rotation leads to an increase in the Coriolis force. Also, the Prandtl number measures the ratio of momentum diffusivity to thermal diffusivity. Hence, increasing Prandtl number consequently means an increase in momentum diffusivity or a decrease in thermal diffusivity or both. It is revealed that velocity profiles increase with increasing rotation, meanwhile, both the primary and secondary velocity profiles decrease with increasing Prandtl number. The increase in velocity profiles as rotation increases is because more kinetic energy is added to the flow as rotation amplifies. A surge in Prandtl number consequently reduces thermal diffusivity while momentum diffusivity increases; this is the reason for the decrease in the velocity profiles as Prandtl number increases. It is worth mentioning that angular speed can be increased or decreased to adjust the flow velocities of Williamson fluid.

Williamson fluid possesses a thinner boundary layer compared to the Newtonian fluid but increasing the Williamson parameter increases the boundary layer. The flow approaches Newtonian flow and the velocity reduces in the process. Hence, the velocity profiles in all directions decrease with increasing Williamson fluid parameter.

5. Conclusion

This study captured the effects of magnetic field strength, rotation and inclination angle on the flow of Williamson fluid in a porous medium. The equations are formulated and solved numerically to produce graphs that illustrate the dynamics of Williamson fluid flow over a rotating inclined surface. The outcomes of this study are summarised below;

1. Velocity profiles reduce in all directions with increasing magnetic field strength, inclination angle and Williamson fluid parameter.
2. While temperature decreases with increasing magnetic field strength and inclination angle
3. Velocity profiles increase in all directions with increasing Coriolis force
4. Velocity profiles decrease in all directions with increasing Prandtl number.
5. The local skin friction and the heat transfer rate decrease with increasing rotation but mass transfer rate increases with increasing rotation.
6. The local skin friction rate increases with increasing Lorentz force but heat and mass transfer rates decrease with increasing Lorentz force.

Author Contributions:

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

”The authors declare no conflict of interest.”