Assessment of breast cancer at all stages is of great importance in medicine because in addition to predicting the growth rate, treatment planning must also be considered. In this study, the new maps named the M\(^{*}_{new}\)(k)-map besides a proper signal-to-noise ratio (SNR) under the corresponding theory as well as new parameters such as Ti and FWHM have been introduced to investigate breast cancer performance. In other words, a new function on the SNR from convolutional combination of the relaxation times in MRI as FD\(_{SNR}\) is suggested which utilizes Fourier transform and differentiating operator. This function may be computed for all T1- and T2- weighted images towards prediction of the growth rate of abnormal tissues. These maps and the parameters may contribute to better diagnosis of breast cancer.
Imaging systems are able to obtain a lot of information on the subject in various situations. Since dissimilar kinds of tissue such as fat, gray or white matter in the brain, cerebral spinal fluid, and cancer possess locally diverse magnetic properties, images created with MR-Imaging show high sensitivity to anatomic disparities and then have high contrast. MRI technique is a potential tool for forming qualified functional and anatomical images and can be used in conjunction with mammography to detect abnormal regions with a high risk of breast tumor or to better examine suspicious areas. In addition, utilizing MR-Imaging is a paired technique that is occasionally used for the breast tumor screening to better realize the true volume of the tumor and to detect other kinds of tumor on and inside the breast [1– 12].
The signal-to-noise ratio (SNR) is a significant element that influences the derived image quality and performance of a distinct system which transfer or process signals, such as imaging systems and data acquisition machines. A high level of SNR transpires that the obtained image is explicit and simple to understand or infer, while a low level of SNR transpires that the resulting image is deteriorated or downgraded through noise and can be difficult to recover or differentiate the interior details. The SNR can be upgraded by different methods, such as rising the signal strength, diminishing the noise level, or by using error correction procedures and filtering undesirable noise. The higher SNR value ensures better accessibility of diagnostic information [13, 14].
In this study, a new criterion on the SNR from convolutional combination of the relaxation times in MRI using the appropriate suggestions is proposed in which of the Fourier transform and differentiator operator is used. This criterion may be computed for all the T\(_1\)– and T\(_2\)– weighted images towards prediction of the growth rate of abnormal tissues.
In this study, the convolution method is applied to the selected images derived from the functions of spin-spin (T\(_{2}\)) and spin-lattice (T\(_{1}\)) relaxation times to attain an eligible image with a better SNR. In MR imaging, the T\(_{2\ }\)or T\(_{1}\)-weighted images are also utilized here to distinguish the normal tissues from tumors or suspicious dense tissues. The T\(_{1}\) and T\(_{2}\) relaxation times may be submitted as macroscopic and microscopic aspects, correspondingly. The magnitudes of the magnetized vectors of transverse M\(_{xy}\) (t) and longitudinal M\(_{z}\) (t) in terms of T\(_{1\ }\)and T\(_{2\ }\)relaxation times are expressed as follows,
\[\label{GrindEQ__1_} \frac{{\mathrm{M}}_{\mathrm{xy}}\left(\mathrm{t}\right)}{{\mathrm{M}}_0}\mathrm{=}\mathrm{\ }{\mathrm{e}}^{\mathrm{-}\frac{\mathrm{t}}{{\mathrm{T}}_{\mathrm{2}}}} ,\text{ and } \frac{{\mathrm{M}}_{\mathrm{z}}\left(\mathrm{t}\right)}{{\mathrm{M}}_0}\mathrm{=}\mathrm{1-\ }{\mathrm{e}}^{\mathrm{-}\frac{\mathrm{t}}{{\mathrm{T}}_{\mathrm{1}}}}. \tag{1}\]
To abstract a few more quantities jointly from these T\(_{1}\)– and T\(_{2}\)-maps, a new function called M\(_{new\ }\)(t) is proposed as below,
\[\label{GrindEQ__2_} {\mathrm{M}}_{\mathrm{new}}\mathrm{(t)=} \mathrm{\ }\frac{{\mathrm{M}}_{\mathrm{xy}}\left(\mathrm{t}\right)}{{\mathrm{M}}_0}\mathrm{\ }\circledast \mathrm{\ }\frac{{\mathrm{M}}_{\mathrm{z}}\left(\mathrm{t}\right)}{{\mathrm{M}}_0} , \tag{2}\] where \(\circledast\) indicates the convolution operator. Using the M\(_{New\ }\)(t) function, which incorporates interactions between both relaxation times via the convolution feature, the magnitudes of \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\) are calculated from below function,
\[\label{GrindEQ__3_} {\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\mathrm{\ }\left(\mathrm{k}\right)\mathrm{=\ }\int^{\mathrm{k}}_0{{\mathrm{M}}_{\mathrm{New}}\left({\mathrm{t}}^{\mathrm{'}}\right)\mathrm{.d}{\mathrm{t}}^{\mathrm{'}}}\ , \tag{3}\] where k is the parameter ranging between zero and one. The derived new maps will be created by the \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\) at various k-parameters. The SNR of the images of \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\mathrm{(k)}\) is computed, and then the Fourier transform of the differentiation of the SNR function as the FD\(_{SNR}\) function is calculated, named new function as follows,
\[\label{GrindEQ__4_} {\mathrm{FD}}_{\mathrm{SNR}}\mathrm{=}\mathrm{FFT\ }\left\{\frac{\mathrm{d}}{\mathrm{dk}}\left(\mathrm{SNR(k)}\right)\right\} . \tag{4}\]
The quantities of Total-index (Ti) defined as mean value of the FD\(_{SNR}\) function, and FWHM as full width at half maximum of this function will be computed for more investigation. The \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\) was simulated by means of Matlab (R2016a, MathWorks Inc., MA) simulator, and assessed with respect to the different relaxation times and the dissimilar magnitudes of k-parameter to achieve the \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\)-map in which the values of SNR, Ti, and FWHM are computed.
The T\(_{1}\) and T\(_{2}\)-weighted MR images derived from abnormal breast were taken into account for examination within our proposed theory. These MR images has been indicated or marked as No. 86 in the reference [15] that here were selected for simulation and generation of the \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\)-map at the different magnitudes of k-parameter ranging between 0.01 and 0.955 by intervals of 0.035, as shown in Figure 1. The new SNR amounts at dissimilar k-parameters were calculated for acquiring the novel maps [13]. The \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\)-map at different k-parameters may predict the breast cancer growth trend.
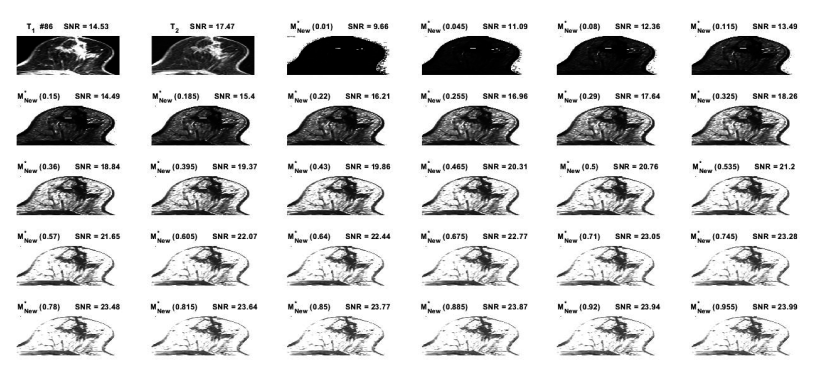
The derived SNR was enhanced at the magnitudes of k-parameters from 0.290 to 0.955, as shown in Figure 2. The maximum derived SNR of 23.99 was at the unique index of k = 0.955.
The new or derived SNR was amplified with the increasing k-parameter, as shown in Figure 2. This behavior may be by virtue of the convolution of two proposed functions as differentiator and integrator, which lead to the maximum point of the new SNR. Here, the k-parameter typifies the interactions between both T\(_{1}\) and T\(_{2}\) relaxation times from the point of view of the quantum characteristics, which should be studied in more details. The intensification of the obtained signal at a certain k-parameter demonstrated that most of the subjects’ data can be transmitted or conveyed through a substitute route that would have been hypothetically satisfactory.
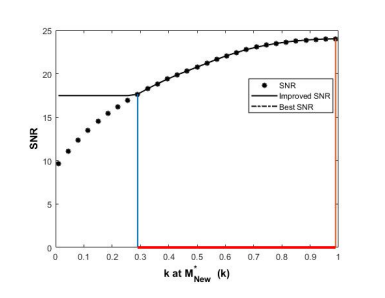
The differentiation of the derived SNR function was decreased with the increasing k-parameter value, as shown in Figure 3.
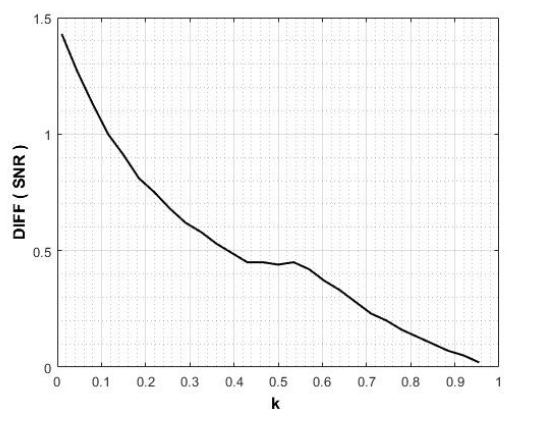
Figure 4 indicates the graph of the FD\(_{SNR}\) fuction in which the values of Ti and FWHM are 0.098 and 3, respectively.
In our previous studies, functions were proposed using only the T\(_{1}\) and T\(_{2}\)-weigthed images with low SNR [16– 18]. To characterize cancer at different steps, the parameters of Ti and FWHM have been introduced in this current research. These maps and the parameters can better aid in diagnosing small breast tumors.
Most breast cancers commence at cellular level that line milk ducts and some in lobules whereas some arise in other tissues. Entirely, the breast cancer is a malignant tumor which begins in a few breast cells. In fact, the breast cancer is regularly a kind of carcinoma known as adenocarcinoma. These carcinomas happen and commence in the glandular tissue [19, 20]. However, other kinds can also happen in the breast, such as sarcomas, that are found in fat and muscle cells as well as in connective tissue. By several instances, a single breast tumor can involve different kinds or a mixture of invasive and malignant cells in situ. Here, the proposed \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\) maps are able to easily identify these groups, allowing for better diagnosis. Besides, the proposed new maps together with the Ti and FWHM parameters are capable to display locally the phases of the breast cancer growth along with the mass quantities. Consequently, the proposed maps are also able to illustrate the breast constructions together with further details in diverse phases with positive correlation coefficient of R\(^{2\ }\)= 0.88. Overall, formation of novel maps be able to assist to avoid further compensations in MR imaging as well as treatment procedures.
Pang et al. [21] have conducted a pilot study to improve the accuracy of dynamic contrast with respect to cell density through a transmembrane water exchange model. When assessing the dependence of ADC on cellular density using diffusion signals of water in tissues, they revealed an intracellular volume fraction of 0.91, which represents a rational extracellular space under a conventional pulsed gradient spin echo (PGSE) sequence. However, no significant correlation between ADC and extravascular extracellular space (v\(_{e}\)) was observed [22, 23] in tumors with a lower intra-to-extracellular water exchange rate constant of k\(_{io}\) amounts, such as breast cancer with an average k\(_{io}\) of about 2.5 s\(^{\mathrm{-}}\)\(^{1}\) [24] and in glioblastoma multiforme (GBM) with an average of 0.57 s\(^{\mathrm{-}}\)\(^{1}\) [25].
MRI imaging has various applications in proper diagnosis, from rehabilitation issues [26, 27] and improvements to psychological [28] and tumor segmentation [29, 30], which directly impacts the initial appropriate recognition by the physician. Since interstitial fluid plays a key role in tumor treatment and drug delivery, Zhao et al. [31] investigated a new MRI measurement technique of low-velocity biological fluid flow using a combined dual inversion recovery preparation and a stimulated echo sequence with phase contrast procedure. They utilized a phantom and xenografts of female BALB/c mouse models of 4T1 breast cancer administered 40 mg/kg losartan to determine tnabihe velocity to be 85\(\mathrm{\pm}\)16 µm/s. On the other hand, Ma et al. [32] presented a rapid T1-weighted mapping technique based on subspace-constrained joint-domain reconstructions using two different sequences, so their proposed interleaved spatiotemporal encoding and inversion recovery gradient echo techniques were not defined for breast tumors with extensive arrays of lobulated ducts and glandular structures embedded in supporting fat and connective tissues. Furthermore, Wang et al. [33] investigated X-nuclei MRI to compare the SNRs derived from different radiofrequency (RF) coils containing two resonant frequencies to attain a more uniform RF field and thus a higher SNR of the surface coil arrays. Additionally, Ianniello et al. [34] built a dual-tuned bilateral \(^{1}\)H/\(^{23}\)Na breast coil for 7T MRI, which provides sufficient SNR to enable sodium breast imaging in less than 10 minutes. Their proposed coil had been composed by two shielded unilateral units, one for each breast, so that each unit has consisted of three nested layers. They reported that the sodium-receiving array increased the SNR by 1.5- to 3-fold compared to the solenoid coil, where the proton SNR loss was \(\mathrm{<}\)10% because of residual interaction with the sodium array. Their coil has enabled in vivo sodium imaging with an isotropic nominal resolution of 2.8 mm (about 5 mm real resolution) in 9:36 minutes.
There is a need for a radioactive manganese (\(^{52}\)Mn) tracer [35] that can be detected and imaged over hours and days, particularly by MRI and positron emission tomography [36, 37]. The most suitable radioisotope for local and confined situations is \(^{52}\)Mn. Regularly, samples such as rats are administered Mn\(^{2+}\) in the form of MnCl\(_{2}\) and/or \(^{52}\)Mn\(^{2+}\) in solution for imaging [38, 39]. This radioisotope can be generated on-site in small, low-energy cyclotrons in medical centers [40– 43]. Often, Gadolinium(III)-based contrast agents (GBCAs) like Magnevist Gd(DTPA)(Meg\(_{2}\)) and Gd(DOTA)(Meg) play a dominant role in contrast-enhanced MRI and are utilized to improve the accuracy of diagnoses and promote the development of safe, nontoxic Gd(III)-free contrast agents [44, 45]. Using a 1.5 T system, Liu et al. [46] analyzed several b-value diffusion-weighted imaging (DWI) and compared them with the apparent diffusion coefficient (ADC) in normal and abnormal breast tissues from intravoxel incoherent motion (IVIM). They reported that tissue diffusivity (D) and ADC amounts were meaningfully lower in malignant tumors than in normal tissues, benign lesions, and simple cysts. Conversely, the relevant perfusion fraction (f) amounts showed higher amounts.
Sundaravadivelu and Santhanakrishnan [47] developed an image processing method utilizing Fuzzy C-means clustering and Artificial Bee Colony optimization on mammogram and MR images with an accuracy of 89.17%. Furthermore, Shokouhi et al. [48] introduced a region-growing algorithm combining Fuzzy C-means clustering and vesselness filtering to segment potential regions in dynamic contrast-enhanced magnetic resonance imaging by 94% accuracy detection of breast lesions. They reduced false positive detections through a discrimination phase based on morphological properties of the breast lesions and kinetic features, which are fed into the support vector machine (SMV) classifier. Despite some progress, Jannatdoust et al. [49] pointed out that computer-aided detection (CAD) systems face challenges such as varying false positive and false negative rates, the complexity of interpreting large-scale image data, variable system performance, and the lack of large-scale researches and multicenter models, which limit suitability and generalizability for clinical implementation. Technical matters, including image artifacts and the need for explainable and reproducible detection algorithms, remain major hurdles. Future areas of focus include developing more robust and generalizable algorithms, integrating explainable AI to improve transparency and trust among clinicians, developing multifunctional AI systems, and incorporating rich language models to improve diagnostic reporting and patient management. In addition, efforts to optimize and standardize MRI protocols aim to increase accessibility, reduce costs, and optimize the use of CAD systems in clinical practice.
In MR imaging, DW imaging protocol optimization comprises selecting a suitable b-value, satisfactory fat suppression, sufficient SNR, and artifact lessening through shimming and/or parallel imaging. In addition, DW imaging post-processing investigation involves standard noise filtering, image registration, and consistent procedures for measuring the region of interest (ROI) for ADC mapping. Also, consistency in DW acquisition timing before or after contrast administration is suggested. Fundamentally, DW imaging is related to the constrained SNR that relays on several parameters. A satisfactory SNR is required for abnormality visibility and for correct ADC mensuration. Since higher SNR can be utilized to enhance the spatial resolution of DW imaging, execution at higher field strength may provide remarkable signal augmentation. Other techniques to enhance SNR comprise growing voxel size such as raising slice thickness and declining spatial resolution in plane. In addition to that, raising the number of averages or declining TE can improve the derived SNR in DW imaging. Meanwhile, a short TE decreases susceptibility artifacts that may happen at higher b-values [50]. Also, the selection of b-value impacts the derived SNR. Jones et al. have been demonstrated that the b-value that offers the greatest SNR for a spin echo DW sequence is b = 1.1/ADC [51]. In breast imaging, with generic reported ADC amounts of 1.6e\(^{-3}\) to 2.0e\(^{-3}\) mm\(^{2}\)/s for normal tissue, it relates to an optimal DW of approximately b = 6.0e+2 s/mm\(^{2}\). Otherwise, a greater b value enhances contrast resolution at the expense of SNR. Here, it should be noted that breasts with low mammographic density, relating to a small volume of fibroglandular tissue, typically have a visually small SNR on DW images when fat suppression is appropriately executed.
Detecting smaller abnormalities (less than 1 cm) remains a challenge in DW imaging by virtue of restricted spatial resolution. Due to existing hardware limitations of most clinical MR scanners, spatial resolution in the echo-planar imaging (EPI) plane for axial bilateral breast imaging is usually limited to 2 mm because of the number of frequency and phase encoding steps which may be acquired before the signal declines and also due to the considered field of view (FOV) [52]. Both greater magnetic field power [53] and different acquisition approaches comprising decreased FOV methods are being examined to attain greater spatial resolution. Nonetheless, tiny tumors may be more easily distinguished when designs are made to decrease magnetic field inhomogeneity and magnetic susceptibility artifacts. The methods based on hand-drawn ROI possess restrictions, comprising the time required to draw ROIs, ROI accuracy, and ROI reproducibility. Several semi-automated approaches to execute voxel-wise studies have revealed the ability to address these issues [54, 55]. Nevertheless, it remains problematic to directly propagate ROIs from dynamic contrast-enhanced (DCE) approach, which tumors are well imagined, because regular distortions of the EPI image lead to positional shifts. Further efforts are required to evaluate the specificity and sensitivity of DW imaging as a single agent without the support of DCE images. There are few data on false-positive ratios relevant to the qualitative clarification of breast DW images, which could be decreased by acquiring greater b-values. Measureable techniques more simplify the distinction between malignant and benign lesions and may help decrease the false-positive ratios in DW imaging.
One of the most regular kinds of tumors in women is breast cancer, which can be screened by joint medical imaging devices. In our research, an quantitative evaluation was approched by introducing a theory and the corresponding proposals that generate new images called \({\mathrm{M}}^{\mathrm{*}}_{\mathrm{New}}\left(\mathrm{k}\right)\)-map together with good SNR in a positive correlation. The parameters Ti and FWHM were introduced to characterize cancer in different stages. These parameters and the derived maps can aid to reclaim breast cancer diagnosis. Moreover, the results can help in counting the initial causes of the breast tumors.
Ashoor, M., & Khorshidi, A. (2023). Modeling modulation transfer function based on analytical functions in imaging systems. The European Physical Journal Plus, 138(3), 249.
Truszkiewicz, A., Aebisher, D., & Bartusik-Aebisher, D. (2020). Assessment of spin-lattice T1 and spin-spin T2 relaxation time measurements in breast cell cultures at 1.5 Tesla as a potential diagnostic tool in vitro. Medical Research Journal, 5(1), 23-33.
de Graaf, R. A., Brown, P. B., McIntyre, S., Nixon, T. W., Behar, K. L., & Rothman, D. L. (2006). High magnetic field water and metabolite proton T1 and T2 relaxation in rat brain in vivo. Magnetic resonance in medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 56(2), 386-394.
Jensen, J. H., & Chandra, R. (2000). MR imaging of microvasculature. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 44(2), 224-230.
Ashoor, M., & Khorshidi, A. (2016). Estimation of the number of compartments associated with the apparent diffusion coefficient in MRI: the theoretical and experimental investigations. American Journal of Roentgenology, 206(3), 455-462.
De Luca, A., Leemans, A., Bertoldo, A., Arrigoni, F., & Froeling, M. (2018). A robust deconvolution method to disentangle multiple water pools in diffusion MRI. NMR in Biomedicine, 31(11), e3965.
Ashoor, M. (2005). Introducing a new definition towards clinical detection of microvascular changes using diffusion and perfusion MRI. Scientia Iranica, 12(1).
Ashoor, M., Khorshidi, A., & Sarkhosh, L. (2019). Estimation of microvascular capillary physical parameters using MRI assuming a pseudo liquid drop as model of fluid exchange on the cellular level. Reports of Practical Oncology and Radiotherapy, 24(1), 3-11.
Ashoor, M., Khorshidi, A., Pirouzi, A., Abdollahi, A., Mohsenzadeh, M., & Barzi, S. M. Z. (2021). Estimation of Reynolds number on microvasculature capillary bed using diffusion and perfusion MRI: the theoretical and experimental investigations. The European Physical Journal Plus, 136(2), 152.
Bushberg, J. T., Seibert, J. A., Leidholdt, E. M., & Boone, J. M. (2002). The Essential Physics of Medical Imaging (2nd ed.). Lippincott Williams & Wilkins. ISBN 0-683-30118-7
Ashoor, M., & Khorshidi, A. (2022). Point-spread-function enhancement via designing new configuration of collimator in nuclear medicine. Radiation Physics and Chemistry, 190, 109783.
Bouzar-Benlabiod, L., Harrar, K., Yamoun, L., Khodja, M. Y., & Akhloufi, M. A. (2023). A novel breast cancer detection architecture based on a CNN-CBR system for mammogram classification. Computers in Biology and Medicine, 163, 107133.
Sage, D., & Unser, M. (2004). Teaching image-processing programming in Java. IEEE Signal Processing Magazine, 20(6), 43-52.
Han, S. H., An, Y. Y., Kang, B. J., Kim, S. H., & Lee, E. J. (2016). Takeaways from pre-contrast T1 and T2 breast magnetic resonance imaging in women with recently diagnosed breast cancer. Iranian Journal of Radiology, 13(4), e36271.
Ashoor, M., & Khorshidi, A. (2024). Improving signal-to-noise ratio by maximal convolution of longitudinal and transverse magnetization components in MRI: application to the breast cancer detection. Medical & Biological Engineering & Computing, 62(3), 941-954.
Ashoor, M., & Khorshidi, A. (2025). Introducing a parametric function on relaxation times in magnetic resonance imaging. Multimedia Tools and Applications, 84(17), 18247-18262.
Ashoor, M., & Khorshidi, A. (2023). Modelling cardiovascular system using Fermi functions on capillary bed. Sādhanā, 48(3), 151.
Khorshidi, A., Ashoor, M., & Abdollahi, A. (2023). Optimization of breast treatment planning towards lower dose rate: a Monte Carlo simulation study. Informatics in Medicine Unlocked, 38, 101220.
Khorshidi, A., & Ashoor, M. (2023). New deformity outline on the breast radiation therapy for diminishing absorbed dose ratio. Brazilian Journal of Radiation Sciences, 11(3), 1-12.
Pang, Z., Wang, Z., Wang, B., Guo, K., Meng, C., Liu, Y., … & Bai, R. (2022). Consideration of transmembrane water exchange in pharmacokinetic model significantly improves the accuracy of DCE-MRI in estimating cellular density: A pilot study in glioblastoma multiforme. Magnetic Resonance Letters, 2(4), 243-254.
Arlinghaus, L. R., Li, X., Rahman, A. R., Welch, E. B., Xu, L., Gore, J. C., & Yankeelov, T. E. (2011). On the relationship between the apparent diffusion coefficient and extravascular extracellular volume fraction in human breast cancer. Magnetic resonance imaging, 29(5), 630-638.
Mills, S. J., Soh, C., Rose, C. J., Cheung, S., Zhao, S., Parker, G. J. M., & Jackson, A. (2010). Candidate biomarkers of extravascular extracellular space: a direct comparison of apparent diffusion coefficient and dynamic contrast-enhanced MR imaging—derived measurement of the volume of the extravascular extracellular space in glioblastoma multiforme. American Journal of Neuroradiology, 31(3), 549-553.
Li, Xin, Wei Huang, Elizabeth A. Morris, Luminita A. Tudorica, Venkatraman E. Seshan, William D. Rooney, Ian Tagge, Ya Wang, Jingang Xu, and Charles S. Springer Jr. “Dynamic NMR effects in breast cancer dynamic-contrast-enhanced MRI.” Proceedings of the National Academy of Sciences 105, no. 46 (2008): 17937-17942.
Bai, R., Wang, B., Jia, Y., Wang, Z., Springer Jr, C. S., Li, Z., … & Liu, Y. (2020). Shutter‐speed DCE‐MRI analyses of human glioblastoma multiforme (GBM) data. Journal of Magnetic Resonance Imaging, 52(3), 850-863.
Gul, S., Sidhu, J. K., Shafi, M. S., & Bhat, I. M. Magnetic resonance imaging features in the tubercular spine: A cross sectional study from North India. Trends in Clinical and Medical Sciences 3(1), 307-314
Nandeesh, S., Sharma, A., Raju, K. P., & Kumar, S. (2023). Study of tibial ACL footprint in patients undergoing ACL reconstruction—correlation between pre-op MRI and intra-op measurements using arthroscopic ruler. Trends in Clinical and Medical Sciences, 3(1), 562–568.
Khorshidi, A. (2024). Examining neural correlates of sexual preferences between Persian homo-and heterosexual males using psychological assessments and functional magnetic resonance imaging in specifying cognitive map: A limited and cross-sectional study. Journal of Pediatric Neurology, 21.
Khorshidi, A. (2023). Segmentation of tumor region in respiratory disease by extended algorithm. International Journal of Modern Physics C, 34(12), 2350164.
Khorshidi, A. (2024). Introducing extended algorithm for respiratory tumor segmentation. Multimedia Tools and Applications, 83(28), 71863-71883.
Zhao, J., Cao, Y., Liu, W., & Han, D. (2023). Non-invasive assessment for intratumoural distribution of interstitial fluid flow. Magnetic Resonance Letters, 3(4), 286-297.
Ma, L., Bao, Q., Martinho, R. P., Chen, Z., & Frydman, L. (2024). Fast T1 mapping MRI in preclinical and clinical settings using subspace-constrained joint-domain reconstructions. Magnetic Resonance Letters, 4(4), 200134.
Wang, G., Yang, H., Li, J., Wen, J., Zhong, K., & Tian, C. (2023). Overview and progress of X-nuclei magnetic resonance imaging in biomedical studies. Magnetic Resonance Letters, 3(4), 327-343.
Ianniello, C., Madelin, G., Moy, L., & Brown, R. (2019). A dual‐tuned multichannel bilateral RF coil for 1H/23Na breast MRI at 7 T. Magnetic Resonance in Medicine, 82(4), 1566-1575.
Khorshidi, A., & Shams-Abadi, M. (2025). Simulation of 52 m+ g Mn production yield via chromium target under low-energy proton irradiation from mashhad small cyclotron. Physics of Particles and Nuclei Letters, 22(3), 586-595.
Khorshidi, A. (2024). Chemical radioanalysis of production of positron-emitting radioisotope Gallium-68 via (p, n) and (p, 2n) reactions using compact cyclotron for tomography applications. Heliyon, 10(10), e31499.
Ashoor, M., & Khorshidi, A. (2019). Evaluation of crystals’ morphology on detection efficiency using modern classification criterion and Monte Carlo method in nuclear medicine. Proceedings of the National Academy of Sciences, India Section A: Physical Sciences, 89(3), 579-585.
Khorshidi, A. (2025). Simulation of 52m+gMn generation yield using chromium target under low-energy proton irradiation at compact cyclotron in Mashhad City. Journal of Multiscale Modelling. Advance online publication.
Khorshidi, A. (2019). Radiochemical parameters of molybdenum-99 transmutation in cyclotron-based production method using a neutron activator design for nuclear-medicine aims. The European Physical Journal Plus, 134(6), 249.
Khorshidi, A. (2023). Nano Yttrium-90 and Rhenium-188 production through medium medical cyclotron and research reactor for therapeutic usages: A simulation study. Nuclear Engineering and Technology, 55(5), 1871-1877.
Khorshidi, A. (2020). Accelerator-based methods in radio-material 9 9 Mo/99mTc production alternatives by monte carlo method: The scientific-expedient considerations in nuclear medicine. Journal of Multiscale Modelling, 11(01), 1930001.
Khorshidi, A. (2019). Molybdenum-99 production via lead and bismuth moderators and milli-structure-98Mo samples by the indirect production technique using the Monte Carlo method. Physics-Uspekhi, 62(9), 931.
Khorshidi, A. (2016). Gold nanoparticles production using reactor and cyclotron based methods in assessment of 196,198 Au production yields by 197Au neutron absorption for therapeutic purposes. Materials Science and Engineering: C, 68, 449-454.
Kalman, F. K., Nagy, V., Váradi, B., Garda, Z., Molnar, E., Trencsenyi, G., … & Tircsó, G. (2020). Mn (II)-based MRI contrast agent candidate for vascular imaging. Journal of Medicinal Chemistry, 63(11), 6057-6065.
Wan, F., Wu, L., Chen, X., Zhang, Y., & Jiang, L. (2023). Research progress on manganese complexes as contrast agents for magnetic resonance imaging. Polyhedron, 242, 116489.
Liu, C., Liang, C., Liu, Z., Zhang, S., & Huang, B. (2013). Intravoxel incoherent motion (IVIM) in evaluation of breast lesions: comparison with conventional DWI. European Journal of Radiology, 82(12), e782-e789.
Sundaravadivelu, B., & Santhanakrishnan, K. (2023). Breast cancer detection using comprising fuzzy c-means and artificial bee colony optimization segmentation and grading with random forest classifier. Traitement du Signal, 40(6), 2751-2759.
B. Shokouhi, S., Fooladivanda, A., & Ahmadinejad, N. (2017). Computer-aided detection of breast lesions in DCE-MRI using region growing based on fuzzy C-means clustering and vesselness filter. EURASIP Journal on Advances in Signal Processing, 2017, 39.
Jannatdoust, P., Valizadeh, P., Saeedi, N., Valizadeh, G., Salari, H. M., Saligheh Rad, H., & Gity, M. (2025). Computer‐aided detection (CADe) and segmentation methods for breast cancer using magnetic resonance imaging (MRI). Journal of Magnetic Resonance Imaging, 61(6), 2376-2390.
Woodhams, R., Ramadan, S., Stanwell, P., Sakamoto, S., Hata, H., Ozaki, M., … & Inoue, Y. (2011). Diffusion-weighted imaging of the breast: principles and clinical applications. Radiographics, 31(4), 1059-1084.
Jones, D. K., Horsfield, M. A., & Simmons, A. (1999). Optimal strategies for measuring diffusion in anisotropic systems by magnetic resonance imaging. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 42(3), 515-525.
Singer, L., Wilmes, L. J., Saritas, E. U., Shankaranarayanan, A., Proctor, E., Wisner, D. J., … & Hylton, N. M. (2012). High-resolution diffusion-weighted magnetic resonance imaging in patients with locally advanced breast cancer. Academic Radiology, 19(5), 526-534.
Hines, C. D., Yu, H., Shimakawa, A., McKenzie, C. A., Brittain, J. H., & Reeder, S. B. (2009). T1 independent, T2* corrected MRI with accurate spectral modeling for quantification of fat: validation in a fat‐water‐SPIO phantom. Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine, 30(5), 1215-1222.
Rahbar, H., Kurland, B. F., Olson, M. L., Kitsch, A. E., Scheel, J. R., Chai, X., … & Partridge, S. C. (2016). Diffusion-weighted breast magnetic resonance imaging: a semiautomated voxel selection technique improves interreader reproducibility of apparent diffusion coefficient measurements. Journal of Computer Assisted Tomography, 40(3), 428-435.
Bisgaard, A. L., Keesman, R., van Lier, A. L., Coolens, C., van Houdt, P. J., Tree, A., … & Mahmood, F. (2023). Recommendations for improved reproducibility of ADC derivation on behalf of the Elekta MRI-linac consortium image analysis working group. Radiotherapy and Oncology, 186, 109803.