On the solution of fractional Riccati differential equations with variation of parameters method

1. Introduction

Linear and non-linear fractional equations play a major role in various fields such as fluid mechanics, optical fibers, solid state physics, chemical physics, probability and statistics, geochemistry, engineering, acoustics and so on [1,2,3,4,5]. This is due to the fact that fractional derivatives can hold the history of the variable under consideration. In fact, several numerical and analytic techniques for solving FDEs have been presented in the literature and they have their own advantages and limitations.

As it is well known, Riccati differential equations concerned with applications in pattern formation in dynamic games, linear systems with Markovian jumps, river flows, econometric models and control theory [6,7,8]. Many studies have been conducted on solutions of the Riccati differential equations. Some of them, the approximate solution of ordinary Riccati differential equation obtained from homotopy perturbation method (HPM) [9,10,11], homotopy analysis method (HAM) [12], and variational iteration method proposed by He [13]. The He’s homotopy perturbation method proposed by He [14,15,16], the variational iteration method [17], Adomian decomposition method (ADM) [18], the Laplace- Adomain- Pade Method [19].

The Variation of Parameters (VPM) is the other name is Variation of constant in Mathematics. The linear conventional differential equations that are inhomogeneous are unraveled by this technique. Duhamel’s rule is another name for this strategy. It was named after Jean-Marie Duhamel \((1797 – 1872) \), by whom this VPM was applied for the absolute first time to tackle the inhomogeneous equation.

By and large to discover arrangement through coordinating components or dubious coefficient with bounty substantially less endeavor, we settle first order inhomogeneous linear differential equations, while heuristics are influenced by the once systems. All the inhomogeneous linear differential equations are not worked by the heuristics which include expecting. The proposed technique is liberated from adjust blunder, discretization, linearization, Adomian’s polynomial and use just beginning condition, which are simpler to actualize and diminish the computational work.

Right now, expand the use of the VPM so as to determine investigative estimated answers for non-linear fractional Riccati differential equation:

\begin{equation*} D^{\alpha}_{\ast} u(t)=A_{1}(t)+A_{2}(t) u(t)+A_{3}(t) u^{2}(t)\,\,\,\,\,\, t\epsilon R, 0 \,< \,\alpha \leq 1, \end{equation*} subject to the initial conditions \begin{equation*} u^{k}(0)=a_{k},\,\,\,\,\,\,\,\, k=1,2,3…..n-1, \end{equation*} where \( \alpha \) is fractional derivative order, n is an integer, A1 (t), A2 (t) and A3 (t) are known real functions and \(a_{k} \) is a constant. The objective of this paper is to broaden the use of the variation of Parameters technique (VPM) to comprehend fractional nonlinear Riccati differential equations with Riemann-Liouville fractional integral.

2. Basic definitions

Here, some fundamental definitions and properties of the fractional calculus hypothesis which can be found in [5,20,21].

1. Definition The Riemann-Liouville fractional primitive of order is of a function \(h:(0,b]\rightarrow R \) of order \( \alpha\epsilon R^{+} \) is defined by \begin{equation*} j^{\alpha}_{0}u(s)=\frac{1}{\Gamma(\alpha)}\int^{t}_{0}(t-s)^{\alpha – 1} u(s)ds, \end{equation*} provided the right side is point wise defined on \((0, b] \) where \( \Gamma \) is the gamma function.

2. Definition The Riemann-Liouville fractional order derivative of function \(u(s) \) is given as

where \( m-1 \leq \alpha\, <\, m \,\epsilon\, Z^{+} \).

3. Definition The modified Riemann-Liouville derivative is defined as \begin{equation*} D^{\alpha}_{\ast,s} u(s)=\frac{1}{\Gamma(m-\alpha)}\frac{d^m}{ds^{m}}\int^{0}_{t}(t-s)^{m-\alpha} (u(s)-u(0))ds, \end{equation*}where \(x\, \epsilon\, [0,1] \), \( m-1 \leq \alpha < m \) and where \( m\geq 1 \).

3.Variation of parameters method

To emanate the main concept of the VPM [22,23] we assume the general equation

\begin{equation*} L(w)+N(w)+R(w)=f(x), \,\,\,\,\,\,\,\,\,\, a \leq x \leq b, \end{equation*} where \(L,\) \(N\) are linear and nonlinear operators. \(R\) is a linear differential operator but \(L\) has the highest order than \(R\), \(f(x)\) is a source term in the given domain \([a,b].\) By utilizing the VPM, we have the pursuing solution of the equation \begin{equation*} w(x)=\sum^{k-1}_{\iota=0}\frac{c_{\iota+1}x^{\iota}}{\iota\,!}+\int_{0}^{x}\lambda(x,\tau)(-N(w)(\tau)-R(w)(\tau)+f(\tau))d\tau, \end{equation*} where \(k \) represent the order of given differential equation (DE) and \(C_{\iota} \) where \( \iota=1,2,3, \) are unknowns. So \begin{equation*} w(x)=\sum^{k-1}_{\iota=0}\frac{c_{\iota+1}x^{\iota}}{\iota\,!}. \end{equation*}

For homogeneous solution which is taken by

\begin{equation*} L(w)= 0. \end{equation*}

The another part which is obtained from Equation (1) by using VPM is

\begin{equation*} \int_{0}^{x}\lambda(x,\tau)(-N(w)(\tau)-R(w)(\tau)+f(\tau))d\tau. \end{equation*}

Here \( \lambda(x,\tau) \) is a Lagrange multiplier that expel the progressive use of integrals in the iterative scheme and it depending on the order of equation. Commonly the pursue definition is utilized to find the value of the multiplier \( \lambda(x,\tau) \) from

\begin{equation*} \lambda(x,\tau)= \sum^{k}_{\iota=1}\frac{(-1)^{\iota-1}\tau^{\iota-1}x^{k-1}}{(\iota-1)\,! (k-1)\,!}=\frac{(x-\tau)^{k-1}}{(k-1)\,!}, \end{equation*} here \(k\) is the order of the given DE and it varies for different values of \(k.\) We have the pursue conditions: \begin{eqnarray*} &&k=1, \,\,\,\,\ \lambda(x,\tau)=1,\\ &&k=2, \,\,\,\, \lambda(x,\tau)=(x-\tau),\\ &&k=3, \,\,\,\,\ \lambda(x,\tau)=\frac{x^{2}}{2\,!}+\frac{\tau^{2}}{2\,!}-\tau x. \end{eqnarray*}

Therefore, we utilize the pursue iterative scheme for solving equation

\begin{equation*} w_{n+1}=w_{0}+\int_{0}^{x}\lambda(x,\tau)(-N(w)(\tau)-R(w)(\tau)+f(\tau))d\tau. \end{equation*}

We can get the initial guess \( w_{0}(x) \) by using initial conditions. We are taking better approximation by using fixed value of initial guess in each iteration. Here we are settling fractional riccati differential condition by utilizing Reimann-Liouville. For the arrangement method we are consolidating VPM with fractional integral then the iterative plan for fractional equations is

\begin{equation*} w_{n+1}=w_{0}+\frac{1}{\Gamma (\alpha)} \int_{0}^{x}\lambda(x,\tau)^{x-\tau}(-N(w)(\tau)-R(w)(\tau)+f(\tau))d(\tau). \end{equation*}

4. Solution of fractional Riccati differential equation

The point of this area is to contemplate the arrangements and the impacts of the fractional order derivative to Riccati’s conditions. In perspective on the nearness of a shut structure arrangement and on other applied numerical procedures to Riccati’s conditions, three models are considered to check the capability of the proposed method.

4.1. Problem

We first consider the following fractional Riccati equation:

\begin{equation*} D^{\alpha}_{\tau}u(t)-2u(t)+u^{2}(t)=1,\,\,\,\,\,\,\, 0 < \alpha \leq 1, t\geq 0, \end{equation*} with homogeneous initial condition \(u(0)=0 \). The exact solution of the above problem is \begin{equation*} u(t)= 1+\sqrt{2}\tanh \left(\sqrt{2}t + \frac{1}{2}\log\left(\frac{\sqrt{2}-1}{\sqrt{2}+1}\right)\right). \end{equation*}

We construct the following iterative scheme for the above problem:

\begin{equation*} u_{n+1}=u_{0}+\frac{1}{\Gamma (\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1}(2u(t)+u^{2}(t)+1)d\tau. \end{equation*}

Taking initial condition \(u(0)=0 \), the following results for \(\alpha=1 \) are produced:

\begin{align*} u_{1}(t)&=t,\\ u_{2}(t)&=t^{2}-\frac{1}{3}t^{3}+t,\\ u_{3}(t)&=t-\frac{1}{63}t^{7}+\frac{1}{9}t^{6}-\frac{1}{15}t^{5}-\frac{2}{3}t^{4}+\frac{1}{3}t^{3}+t^{2},\end{align*} \begin{align*} u_{4}(t)&=t-\frac{1}{59535}t^{15}+\frac{1}{3969}t^{14}-\frac{41}{36855}t^{13}-\frac{1}{1890}t^{12}+\frac{27}{1925}t^{11}\\ &\;\;\;-\frac{62}{4725}t^{10}-\frac{62}{945}t^{9}+\frac{17}{420}t^{8}+\frac{71}{315}t^{7}+\frac{4}{45}t^{6}-\frac{3}{5}t^{5}-\frac{1}{3}t^{4} +\frac{1}{3}t^{3}+t^{2}. \end{align*}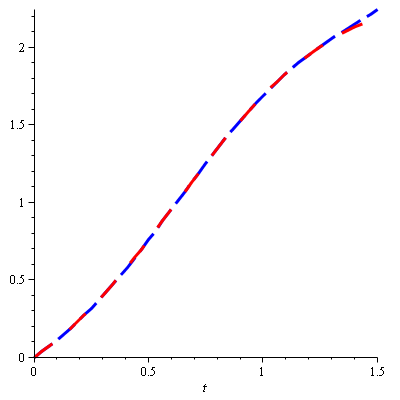

Table 1. Comparison of numerical results of problem 4.1 for \(\alpha\)=1.

t	Exact	VPM	HPM	OHM	Error of VPM
0.0	0.0000000	0.0000000	0.0000000	0.0000000	0.0000000
0.2	0.2419744004	0.2419499764	0.2419648204	0.2443164581	\(2.4424\times 10^{-5}\)
0.4	0.5678068604	0.5673979034	0.5681149562	0.5702708053	\(4.089\times 10^{-4}\)
0.6	0.9535582813	0.9525886597	0.9582588343	0.9535657064	\(9.696\times 10^{-4}\)
0.8	1.346354258	1.345789984	1.365239549	1.3475927635	\(5.64\times 10^{-4}\)
1.0	1.689488974	1.688651308	1.723809524	1.6907027573	\(8.37\times 10^{-4}\)

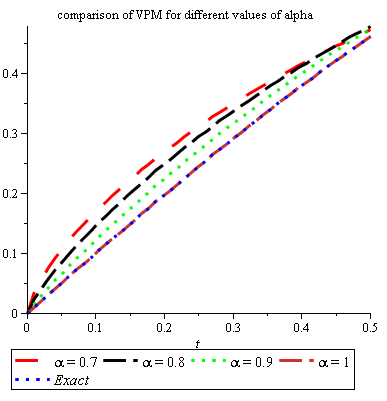
The approximate solutions \(u_{4}(t)\) for different values of \( 0 \,< \,\alpha\leq 1 \) continuously approaches to the exact solution when \( \alpha=1 \). Thus, we anticipate a veracious solution for various values of \( \alpha \). For additional examination Table 1 and Table 2 show a correlation between our methodology and other existing numerical and diagnostic strategies for \( \alpha=1 \). It tends to be found from the table that the outcomes got by the 3-term VPM gives estimated arrangement contrast well overall and different strategies, particularly when draws near to 1. Correlation shows that our strategy gives minimal blunder as contrast with other. Figure 1 is plotted for approximate solution of VPM and exact solution of Problem 4.1. In Figure 2, we have shown the graphic representation of of approximate solution of Problem 4.1 for \(\alpha\) = 0.7, 0.8, 0.9, and 1.

Table 2. Comparison of numerical results of problem 4.1 for different values of \(\alpha\).

t	\(\alpha=0.7\)	\(\alpha=0.8\)	\(\alpha=0.9\)
0.0	0.0000000	0.0000000	0.0000000
0.2	0.3784548231	0.3336603491	0.2867654164
0.4	0.7083751809	0.6756546260	0.6251501607
0.6	1.022225529	1.025455098	0.9976478322
0.8	1.304871418	1.352852736	1.363764296
1.0	1.542084537	1.628041223	1.677804452

4.2. Problem

We consider the fractional Riccati equation,

\begin{equation*} D^{\alpha}_{\tau}u(t)+u^{2}(t)=1,\,\,\,\,\,\,\, 0 < \alpha \leq 1, t\geq 0, \end{equation*} with homogeneous initial condition \(u(0)=0 \). The exact solution of the above problem is \begin{equation*} u(t)=\frac{e^{2t}-1}{e^{2t}+1}. \end{equation*}

We are constructing the following iterative scheme of the above problem is

\begin{equation*} u_{n+1}=u_{0}+\frac{1}{\Gamma (\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1}(-u^{2}(t)+1)d\tau. \end{equation*}

Taking initial condition \(u(0)=0 \), the following results for \( \alpha=1 \) are produced:

\begin{align*} u_{1}(t)&=t,\\ u_{2}(t)&=t-\frac{1}{3}t^{3},\\ u_{3}(t)&=t-\frac{1}{63}t^{7}+\frac{2}{15}t^{5}-\frac{1}{3}t^{3},\\ u_{4}(t)&=t-\frac{1}{59535}t^{15}+\frac{4}{12285}t^{13}-\frac{134}{51975}t^{11}+\frac{38}{2835}t^{9}-\frac{17}{315}t^{7}+\frac{2}{15}t^{5}-\frac{1}{3}t^{3}. \end{align*}

Table 3 and Table 4 show a comparison between our approach and other existing numerical and analytic methods for \(\alpha= 1\). It can be deduced from the tables that the results obtained by the 3-term VPM gives approximate solution compare very well with other methods especially when \(\alpha\) gets close to 1. Comparison shows that our proposed technique gives the least error as compare to other. Figure 3 is plotted for approximate solution of VPM and exact solution of Problem 4.2. In Figure 4, we have shown the graphic representation of approximate solution of Problem 4.2 for \(\alpha\) = 0.7, 0.8, 0.9, and 1.

Table 3. Comparison of numerical results of problem 4.2 for \(\alpha=1\).

t	Exact	VPM	HPM	OHM	Error of VPM
0.0	0.0000000	0.0000000	0.0000000	0.0000000	0.0000000
0.2	0.1973753203	0.1973753160	0.1973753092	0.1974023559	\(4\times 10^{-9}\)
0.4	0.3799489622	0.3799469862	0.3799435784	0.3800652965	\(1.976\times 10^{-6}\)
0.6	0.5370495670	0.5369833784	0.5368572343	0.5371479432	\(6.61886\times 10^{-5}\)
0.8	0.6640367702	0.6633009217	0.6617060368	0.6640492005	\(7.3584\times 10^{-4}\)
1.0	0.7615941560	0.7571662667	0.7460317460	0.7616344154	\(4.427\times 10^{-3}\)

Table 4. Comparison of numerical results of problem 4.2 for different values of \(\alpha\).

t	\(\alpha=0.7\)	\(\alpha=0.8\)	\(\alpha=0.9\)
0.0	0.0000000	0.0000000	0.0000000
0.2	0.2695421965	0.2490582911	0.2242652315
0.4	0.4163894367	0.4130176413	0.4003438466
0.6	0.5223419886	0.5373149545	0.5419937918
0.8	0.6012630211	0.6311970814	0.6517859873
1.0	0.6595756101	0.6995721576	0.7318890064

4.3. Problem

We consider the following fractional Riccati equation,

\begin{equation*} D^{\alpha}_{\tau}u(t)+u(t)-u^{2}(t)=1,\,\,\,\,\,\,\, 0 < \alpha \leq 1, t\geq 0, \end{equation*} with initial condition \( u(0)=\frac{1}{2} \). The exact solution of the above problem is \begin{equation*} u(t)=\frac{e^{-t}}{e^{t}+1}. \end{equation*}

We are constructing the following iterative scheme of the above problem is

\begin{equation*} u_{n+1}=u_{0}+\frac{1}{\Gamma (\alpha)} \int_{0}^{t}(t-\tau)^{\alpha-1}(u^{2}(t)+u(t))d\tau. \end{equation*}

Taking initial condition \(u(0)=0 \), the following results for \( \alpha=1 \) are produced:

\begin{align*} u_{1}(t)&=\frac{1}{2}-\frac{1}{4}t,\\ u_{2}(t)&=\frac{1}{2}-\frac{1}{4}t+\frac{1}{48}t^{3},\\ u_{3}(t)&=\frac{1}{2}-\frac{1}{4}t+\frac{1}{48}t^{3}+\frac{1}{16128}t^{7}-\frac{1}{480}t^{5},\\ u_{4}(t)&=\frac{1}{2}-\frac{1}{4}t+\frac{1}{3901685760}t^{15}-\frac{1}{50319360}t^{13}+\frac{67}{106444800}t^{11} -\frac{19}{1451520}t^{9}+\frac{17}{80640}t^{7}-\frac{1}{480}t^{5}+\frac{1}{48}t^{3}. \end{align*}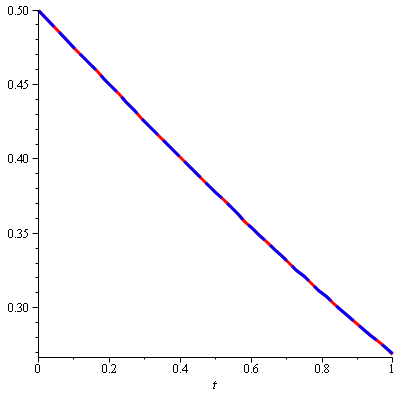

Table 5. Comparison of numerical results of problem 4.3 for different values of \(\alpha\).

t	Exact	\(\alpha=0.7\)	\(\alpha=0.8\)	\(\alpha=0.9\)	\(\alpha=1.0\)	Error
0.0	0.5000000000	0.5000000000	0.5000000000	0.5000000000	0.5000000000	0.00000000
0.2	0.4501660027	0.4309494485	0.4365457215	0.4431444975	0.4501660027	0.00000000
0.4	0.4013123399	0.3893257986	0.3909330219	0.3951259688	0.4013123420	\(-2.1\times 10^{-9}\)
0.6	0.3543436938	0.3553599726	0.3517080337	0.3515020203	0.3543437718	\(-7.80\times 10^{-8}\)
0.8	0.3100255189	0.3262525572	0.3171054591	0.3117623165	0.3100265069	\(-9.880\times 10^{-7}\)
1.0	0.2689414214	0.3007743319	0.2863305011	0.2757427983	0.2689483336	\(-6.912\times 10^{-6}\)

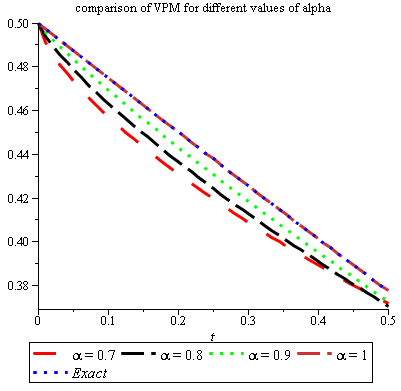
Table 5 represents the different values of \(\alpha\). We see that VPM for \(\alpha=1\) gives the best approximate results with least computational work. Figure 5 is plotted for approximate solution of VPM and exact solution of Problem 4.3. In Figure 6, we have shown the graphic representation of approximate solution of Problem 4.3 for \(\alpha=\) 0.7, 0.8, 0.9, and 1.

In above all problems, it seems that \(u_{4}(t)\) for equal to 1 is in high agreement with the exact solution. Furthermore, \(u_{4}(t)\) for different values of continuously communicates until \(\alpha=1\) is reached. Thus, a convenient solution is expected for various values of \(\alpha\).

5. Discussion of Results:

We have adequately applied the variation of Parameters procedure (VPM) for the numerical outcomes of fractional order riccati’s differential condition. We got pleasing results due to great intermingling VPM.

6. Concluding Remarks:

In this work, we utilized the Variation of Parameters Method (VPM) to study the solution of the fractional Riccati equation. We succeed to the fact that VPM is very practical and effective technique for finding the analytic results and in addition numerical results for extensive classes of linear and nonlinear fractional differential equations. It provides the solutions in very less iteration and that converge very rapidly in real physical problems. Three existing models were tested to noticeable the legitimacy of the chosen technique and the attained outcomes were outstanding and compatible with other methods. Furthermore, we noticed that the attained approximate results for various values of alpha continuously communicate until the first order derivative is reached. This is another indicator that our results are likely to be valid.

acknowledgments

We would like to thank the reviewers for carefully reading the manuscript and making several helpful comments to increase the quality of the paper.

authorcontributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

conflictofinterests

The authors declare no conflict of interest.