A carbon nanotube (CNT) is a miniature cylindrical carbon structure that has hexagonal graphite molecules attached at the edges. In this paper, we compute the numerical invariant (Topological indices) of linear [n]-phenylenic, lattice of \(C_{4}C_{6}C_{8}[m, n]\), \(TUC_{4}C_{6}C_{8}[m, n]\) nanotube, \(C_{4}C_{6}C_{8}[m, n]\) nanotori.

| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,2)\) | \(6\) |
| \((2,3)\) | \(4n-4)\) |
| \((3,3)\) | \(4n-4\) |
Theorem 3.1. Consider the graph \(T\) of a linear[n]-phenylenic. Then the \(AG_{1}\) , \(SK\), \(SK_{1}\) and \(SK_{2}\) indices of \(T\) are equal to
Proof. 1. \begin{eqnarray*} AG_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=&|E_{1}(G)|\frac{2+2}{2\sqrt{2.2}}+|E_{2}(G)|\frac{2+3}{2\sqrt{2.3}}\\ &&+|E_{3}(G)|\frac{3+3}{2\sqrt{3.3}}\\ &=& 6(1)+(4n-4)\left(\frac{5}{2\sqrt{6}}\right)+(4n-4)(1)\\ &=&8.08n-2.08. \end{eqnarray*} 2. \begin{eqnarray*} SK(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2+2}{2}+|E_{2}(G)|\frac{2+3}{2}\\ &&+|E_{3}(G)|\frac{3+3}{2}\\ &=&12+10n-10+ 12n-12\\ &=&22n -10. \end{eqnarray*} 3. \begin{eqnarray*} SK_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2.2}{2}+|E_{2}(G)|\frac{2.3}{2}\\ &&+|E_{3}(G)|\frac{3.3}{2}\\ &=&=12+12n-12+ 18n-18\\ &=&30n-18. \end{eqnarray*} 4. \begin{eqnarray*} SK_{2}(G)&=& \sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}+\sum\limits_{uv\in E_{2}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=&|E_{1}(G)|\left(\frac{2+2}{2}\right)^{2}+|E_{2}(G)|\left(\frac{2+3}{2}\right)^{2}\\ &&+|E_{3}(G)|\left(\frac{3+3}{2}\right)^{2}\\ &=&24+25n-25+ 36n-36\\ &=&61n-37. \end{eqnarray*}
In continue of this section, we see the following figures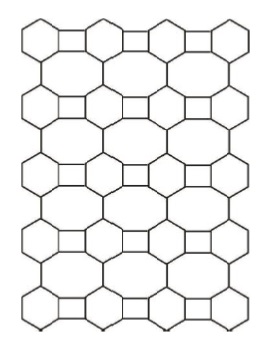
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,2)\) | \(2n+4\) |
| \((2,3)\) | \(4m+4n-8\) |
| \((3,3)\) | \(9mn-8n-5m+4\) |
Theorem 3.2. Consider the graph \(T\) of a linear[n]-phenylenic. Then the \(AG_{1}\), \(SK,\) \(SK_{1}\) and \(SK_{2}\) indices of \(T\) are equal to
Proof. 1. \begin{eqnarray*} AG_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=&|E_{1}(G)|\frac{2+2}{2\sqrt{2.2}}+|E_{2}(G)|\frac{2+3}{2\sqrt{2.3}}\\ &&+|E_{3}(G)|\frac{3+3}{2\sqrt{3.3}}\\ &=& 9mn-5.92m-9.92n-3.04\\ &=&=(9n-5.92)m-9.92n-3.84. \end{eqnarray*} 2. \begin{eqnarray*} SK(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2+2}{2}+|E_{2}(G)|\frac{2+3}{2}\\ &&+|E_{3}(G)|\frac{3+3}{2}\\ &=&= 4n+8+10m+10n-20+27mn-24n-15m+12\\ &=&27mn-10n-5m. \end{eqnarray*} 3. \begin{eqnarray*} SK_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2.2}{2}+|E_{2}(G)|\frac{2.3}{2}\\ &&+|E_{3}(G)|\frac{3.3}{2}\\ &=&=4n+8+12m+12n-24+40.5mn-36n-22.5m+8\\ &=&(40.5n-10)m-20n+2. \end{eqnarray*} 4. \begin{eqnarray*} SK_{2}(G)&=& \sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}+\sum\limits_{uv\in E_{2}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=&|E_{1}(G)|\left(\frac{2+2}{2}\right)^{2}+|E_{2}(G)|\left(\frac{2+3}{2}\right)^{2}\\ &&+|E_{3}(G)|\left(\frac{3+3}{2}\right)^{2}\\ &=&8n+16+25m+25n-100+81mn-72n-45m+36\\ &=&(81n-20)m-39n-48. \end{eqnarray*}

| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,3)\) | \(4n\) |
| \((3,3)\) | \(9mn-5m\) |
Theorem 3.3. Consider the graph \(T\) of a linear[n]-phenylenic. Then the \(AG_{1}\), \(SK,\) \(SK_{1}\) and \(SK_{2}\) indices of $T$ are equal to
Proof. 1. \begin{eqnarray*} AG_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=&|E_{1}(G)|\frac{2+3}{2\sqrt{2.2}}+|E_{2}(G)|\frac{3+3}{2\sqrt{2.3}}\\ &=& 9mn-5m+4.08m\\ &=&(9n-0.92)m. \end{eqnarray*} 2. \begin{eqnarray*} SK(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2+3}{2}+|E_{2}(G)|\frac{3+3}{2}\\ &=&10m+27mn-15m\\ &=&(27n-5) m. \end{eqnarray*} 3. \begin{eqnarray*} SK_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2.3}{2}+|E_{2}(G)|\frac{3.3}{2}\\ &=&=12mn+(9mn-5m)(4.5)\\ &=&(40.5n-10.5)m. \end{eqnarray*} 4. \begin{eqnarray*} SK_{2}(G)&=& \sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}+\sum\limits_{uv\in E_{2}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=&|E_{1}(G)|\left(\frac{2+3}{2}\right)^{2}+|E_{2}(G)|\left(\frac{3+3}{2}\right)^{2}\\ &=&25m+81mn-45m\\ &=&(81n-20) m. \end{eqnarray*}
