The zeroth-order general Randić index of a simple connected graph G is defined as \(R_{\alpha}^{0}(G)=\sum_{u\in V(G)} \big(d(u)\big)^{\alpha}\), where \(d(u)\) is the degree of \(u\) and \(\alpha\not\in \{0,1\}\) is a real number. A \(k\)-polygonal cactus is a connected graph in which every edge lies in exactly one cycle of length \(k\). In this paper, we present the extremal \(k\)-polygonal cactus with \(n\) cycles for \(k\geq3\) with respect to the zeroth-order general Randić index.
Throughout this paper, \(G\) denotes a simple connected undirected graph with vertex set \(V(G)\) and edge set \(E(G)\). Let \(d_G(u)\) and \(N_G(u)\) be the degree and neighbor set of vertex \(u\) in \(G\), respectively. \(n_G(j)\) is the number of the vertices with degree \(j\) in \(G\). For a connected graph \(G\) with \(u\in V(G)\), if \(G-u\) is not connected, then \(u\) is called a cut-vertex of \(G\). Let \(X\) be a subset of \(V(G)\), we use \(G[X]\) to denote the subgraph of \(G\) induced by \(X\).
A cactus graph , or cactus for short, is a connected graph in which no edge lies in more than one cycle. Consequently, each block of a cactus is either an edge or a cycle. A cycle of length \(k\) is denoted by \(C_k\), and \(C_k\) is always called a \(k\)-polygon in the sequel. If each block of a cactus \(G\) is a \(k\)-polygon, then \(G\) is called a \(k\)-polygonal cactus . Hereafter, if there is no risk of confusion, we always call a \(k\)-polygon as a polygon, and we always simplify \(d_G(u)\) and \(N_G(u)\) as \(d(u)\) and \(N(u)\), respectively.
Let \(\mathcal {G}_{n,k}\) be the class of \(k\)-polygonal cacti with \(n\geq3\) blocks. Suppose that \(G\in \mathcal {G}_{n,k}\) . If \(C_k\) contains exactly one cut-vertex, then \(C_k\) is called a pendent polygon . While \(C_k\) is called a non-pendent polygon if \(C_k\) contains at least two cut-vertices.
A cactus chain is a special \(k\)-polygonal cactus graph such that each polygon has at most two cut-vertices, and each cut-vertex is shared by exactly two polygons. When \(G\) is a cactus chain, then the number of polygons is called the length of \(G\). For convenience, we use the notation \(\mathcal{T}_{n,k}\) to denote the class of cactus chains of length \(n\) such that each polygon is a \(k\)-polygon. From the definition, each cactus chain of \(\mathcal{T}_{n,k}\) has exactly \(n-2\) non-pendent polygons and two pendent polygons. When \(k=3\) and \(n\geq 3\), it is easy to see that the cactus chain of \(\mathcal{T}_{n,k}\) is unique. However, when \(k\geq4\) and \(n\geq3\), \(\mathcal{T}_{n,k}\) is not unique.
A star-like cactus \(W_{n,k}\) is a special \(k\)-polygonal cactus graph with \(n\) polygons such that all polygons have a common vertex. From the definition, \(W_{n,k}\) is unique and all polygons of \(W_{n,k}\) are pendent polygons and \(W_{n,k}\) contains exactly one vertex with degree being equalto \(2n\) and the degree of all the other vertices of \(W_{n,k}\) is equal to two.
Among all the vertex-degree-based graph invariants, the first Zagreb index \(M_1(G)\) [1] and zeroth-order Randić index \(R^{0}(G)\) [2] are two famous topological indices, where $$M_{1}(G)=\sum_{u\in V(G)} \big(d(u)\big)^{2},\,\,\text{and}\,\,R^{0}(G)=\sum_{u\in V(G)} \big(d(u)\big)^{-\frac{1}{2}}.$$ In what follows, \(\alpha\) always denotes a real number such that \(\alpha\not\in \{0,1\}\). As a generalization of \(M_1(G)\) and \(R^{0}(G)\), Li and Zheng [3] put forward the concept of first general Zagreb index \(R_{\alpha}^{0}(G)\), where $$ R_{\alpha}^{0}(G)=\sum_{u\in V(G)} \big(d(u)\big)^{\alpha}.$$ From the definition, it is easy to see that \(M_1(G)=R_{2}^{0}(G)\) and \(R^{0}(G)=R_{-\frac{1}{2}}^{0}(G)\). In some literature, \(R_{\alpha}^{0}(G)\) is also called the zeroth-order general Randić index of \(G\) [4, 5, 6].
In what follows, denote by $$\Phi(n,k,\alpha)=\big(n-1\big)4^{\alpha}+\big(nk-2n+2\big)2^{\alpha},\,\,\text{and}\,\,\, \Psi(n,k,\alpha)=\big(2n\big)^{\alpha}+n\big(k-1\big)2^{\alpha}.$$ Recently, the research on zeroth-order general Randić index of cacti had attracted more and more attention. For instance, Ali et al. [4] characterized the extremal polyomino chains with respect to the zeroth-order general Randić index, Hua et al. [6] identified the extremal unicycle graphs with maximum and minimum zeroth-order genenral Randić index and Hu et al. [5] determined the extremal connected \((n,m)\)-graphs with minimum and maximum zeroth-order general Randić index. In this paper, we shall determine the extremal \(k\)-polygonal cactus with \(n\geq 3\) cycles for \(k\geq3\) with respect to the zeroth-order general Randić index, that is,Theorem 1.1. Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\), where \(n\geq3\), \(k\geq3\) and \(\alpha\) is a real number.
\((i)\) If \(\alpha 1\), then \(\Phi(n,k,\alpha)\leq R_{\alpha}^{0}(G)\leq \Psi(n,k,\alpha)\), where the left equality holds if \(G\in\mathcal{T}_{n,k}\) and the right equality holds if and only if \(G \cong W_{n,k}\).
\((ii)\) If \(0< \alpha< 1\), then \(\Psi(n,k,\alpha)\leq R_{\alpha}^{0}(G)\leq \Phi(n,k,\alpha)\), where the left equality holds if and only if \(G \cong W_{n,k}\) and the right equality holds if \(G\in\mathcal{T}_{n,k}\).
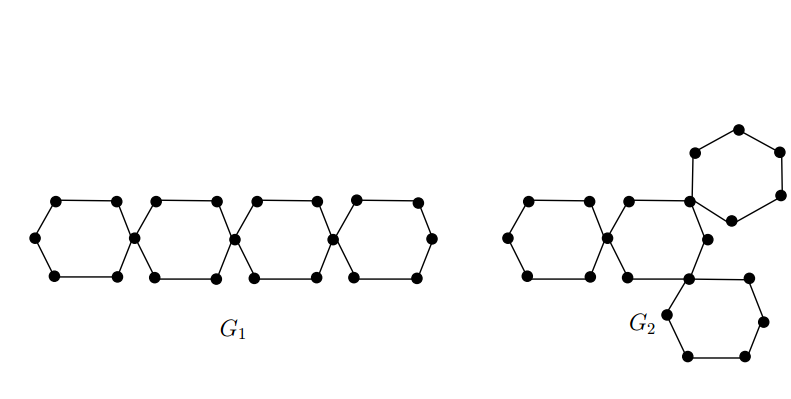
Remark 1.2. It is easy to see that \(\mathcal{T}_{n,k}\) is unique for \(k=3\) and \(n\geq3\), but not unique for \(k\geq4\) and \(n\geq3\). By Theorem 1.1, \(R_{\alpha}^{0}(G)=\Phi(n,k,\alpha)\) holds for every cactus \(G\in \mathcal{T}_{n,k}\). Furthermore, the cacti of \(\mathcal{T}_{n,k}\) are not all the extremal cacti of Theorem 1.1, to see this, let \(G_1\) and \(G_2\) be the two cacti as shown in Fig.1. By an elementary computation, we have \(R_{\alpha}^{0}(G_1)=R_{\alpha}^{0}(G_2)=\Phi(4,6,\alpha)\), but \(G_2\not\in \mathcal{T}_{4,6}\).
Lemma 2.1. Let \(f(x)=x^{\alpha}-(x-2)^{\alpha}\). If \(x>2\), then \(f(x)\) is decreasing for \(0< \alpha< 1 \) and increasing for \(\alpha1\).
Proof. By Lagrange’s mean value theorem, \(f'(x)=\alpha\left(x^{\alpha-1}-(x-2)^{\alpha-1}\right)=2\alpha(\alpha-1)\Theta^{\alpha-2}\), where \(x>2\) and \(x-2< \Theta < x\). It is easy to see that \(f'(x)\) is negative for \(0 < \alpha < 1\) and \(f'(x)\) is positive for \(\alpha 1\). Thus, the result holds.
Recall that \(\mathcal{T}_{n,k}\) is the class of cactus chains of length \(n\) such that each polygon is a \(k\)-polygon. From the definition, if \(k=3\) and \(n\geq3\), then \(\mathcal{T}_{n,k}\) is unique. However, when \(k\geq4\) and \(n\geq3\), \(\mathcal{T}_{n,k}\) is not unique. On the other hand, \( W_{n,k}\) is always unique when \(k\geq3\) and \(n\geq3\). The following result implies that \(R_{\alpha}^{0}(G)\) is a constant for either \(G\in \mathcal{T}_{n,k}\) or \(G\cong W_{n,k}\).Lemma 2.2. Let \(k\geq3\) and \(n\geq1\) be two integers. \((i)\) If \(G\in \mathcal{T}_{n,k}\), then \(R_{\alpha}^{0}(G)=\big(n-1\big)4^{\alpha}+\big(nk-2n+2\big)2^{\alpha}\). \((ii)\) If \(G\cong W_{n,k}\), then \(R_{\alpha}^{0}(G)=\big(2n\big)^{\alpha}+n\big(k-1\big)2^{\alpha}\).
Proof. \((i)\) If \(G\in \mathcal{T}_{n,k}\), then \(n_G(4)=n-1\) and \(n_G(2)=nk-2n+2\). Thus, we have $$R_{\alpha}^{0}(G)=\sum_{u\in V(G)} (d(u))^{\alpha}=\big(n-1\big)4^{\alpha}+\big(nk-2n+2\big)2^{\alpha}.$$
\((ii)\) If \(G\cong W_{n,k}\), then \(n_G(2n)=1\) and \(n_G(2)=n(k-1)\). Thus, we have $$ R_{\alpha}^{0}(G)=\sum_{u\in V(G)} (d(u))^{\alpha}=\big(2n\big)^{\alpha}+n\big(k-1\big)2^{\alpha}.$$ This completes the proof of this result.
To prove our main results, we need to introduce more definitions, which were raised in [7]:Definition 2.3. Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\) and let \(C^{(1)}_{k}\), \(C^{(2)}_{k}\), \(\ldots,\) \(C^{(s+t)}_{k}\) be \(s+t\) cycles of length \(k\) of \(G\) such that \(G\left[V\left(C^{(1)}_{k}\right)\cup V\left(C^{(2)}_{k}\right)\cup \cdots \cup V\left(C^{(s)}_{k}\right)\right]\) and \(G\Big[V\left(C^{(s+1)}_{k}\right)\cup V\left(C^{(s+2)}_{k}\right)\cup \cdots \cup V\left(C^{(s+t)}_{k}\right)\Big]\) are two pendent cactus chains of length \(s\geq 1\) and \(t\geq 1\), respectively.
\((i)\) If \(u_0\in V\left(C^{(1)}_{k}\right)\cap V\left(C^{(s+1)}_{k}\right)\) and \(d_G(u_0)\geq 6\), then \(u_0\) is called a singular vertex of \(G\).
\((ii)\) If \(C^{(0)}_k\) is a \(k\)-polygon of \(G\) with at least three cut vertices in \(G\) such that \(V\left(C^{(1)}_{k}\right)\cap V\left(C^{(0)}_{k}\right)=\{v_0\}\) and \(V\left(C^{(s+1)}_{k}\right)\cap V\left(C^{(0)}_{k}\right)=\{w_0\}\) with \(d_G(w_0)=d_G(v_0)=4\), then \(C^{(0)}_k\) is called a special polygon of \(G\).Lemma 2.4. Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\), where \(k\geq 3\) and \(n\geq3\). If \(G\) contains a singular vertex, then \(R_{\alpha}^{0}(G)\) is neither minimum for \(\alpha1\) and not maximum for \(0 < \alpha< 1\) in \( \mathcal{G}_{n,k}\).
Proof. By contradiction, we assume that \(R_{\alpha}^{0}(G)\) is minimum for \(\alpha1\) and maximum for \(0< \alpha< 1\) in \( \mathcal{G}_{n,k}\). Let \( u_0 \) be a singular vertex of \(G\) with \(d_G(u_0)=2r\), where \(r\geq 3\). For convenience, we suppose that \(u_0\) is a common vertex of two pendent cactus chains \(L_{t,k}\) and \(L_{s,k}\) in \(G\), where \(s\geq t\geq 1\). Suppose that \(C^{(t)}_k=u_1u_2\cdots u_ku_1\) and \(C^{(s)}_k=w_1w_2\cdots w_kw_1\) are the pendent polygons of \(L_{t,k}\) and \(L_{s,k}\), respectively, such that \(u_1\) and \(w_1\) are two cut-vertices of \(G\). Let \(G'=G-u_1u_2-u_1u_k+w_2u_2+w_2u_k\). By the definition of \(G'\), it it easy to see that
Observation 1.
If \(t\geq 2\), then \(u_0\) is also a singular vertex of \(G’\) such that \(u_0\) is a common vertex of two pendent cactus chains \(L_{t-1,k}\) and \(L_{s+1,k}\) in \(G’\).
We consider the following two cases:
Case 1. \(t=1\).
From the definition, we have
\begin{eqnarray*}
\ R_{\alpha}^{0}(G)-R_{\alpha}^{0}(G’)=(2r)^\alpha+2^{\alpha}-(2r-2)^\alpha-4^{\alpha}
=(2r)^\alpha-(2r-2)^\alpha-(4^{\alpha}-2^{\alpha}).
\end{eqnarray*}
By lemma 2.1, since \(2r\geq6>4\), it is easy to see that \(R_{\alpha}^{0}(G)>R_{\alpha}^{0}(G’)\) for \(\alpha1\) and \(R_{\alpha}^{0}(G)< R_{ \alpha}^{0}(G') \) for \(0< \alpha< 1\). No matter which case happens, we can reach a contradiction.
Case 2. \(t\geq2\).
If \(t\geq2\), then from the definition, we have
\begin{eqnarray*}
\ R_{\alpha}^{0}(G)-R_{\alpha}^{0}(G’)&=&4^{\alpha}+2^{\alpha}-2^{\alpha}-4^{\alpha}=0
\end{eqnarray*}
Now, by Observation 1 and above equality, there exists a cactus \(G’\) of \(\mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G)=R_{\alpha}^{0}(G’)\), \(u_0\) is also a singular vertex of \(G’\) and \(u_0\) is a common vertex of two pendent cactus chains \(L_{t-1,k}\) and \(L_{s+1,k}\) in \(G’\). By repeating the above process, we can conclude that there exists a cactus \(G_1\) of \(\mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G)=R_{\alpha}^{0}(G_1)\), \(u_0\) is also a singular vertex of \(G_1\) and \(u_0\) is a common vertex of two pendent cactus chains \(L_{1,k}\) and \(L_{s+t-1,k}\) in \(G_1\).
Now, from the above arguments and Case 1, we can conclude that there exists cactus \(G_0\) of \(\mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G)>R_{\alpha}^{0}(G_0)\) for \(\alpha1\) and \(R_{\alpha}^{0}(G)< R_{\alpha}^{0}(G_0)\) for \(0< \alpha< 1 \), and \(G_0\) contains no singular vertex, a contradiction. Thus, the result holds.
Lemma 2.5. Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\), where \(n\geq4\) and \(k\geq 3\). If \(G\) contains a special polygon, then there exists \(G_0\in \mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G_0)\leq R_{\alpha}^{0}(G)\) for \(\alpha1\) and \(R_{\alpha}^{0}(G_0)\geq R_{\alpha}^{0}(G)\) for \(0< \alpha< 1\) and \(G_0\) contains no special polygon.
Proof. Let \(C^{(0)}_k\) be a special polygon, and let \(L_{t,k}\) and \(L_{s,k}\) be two pendent cactus chains of \(G\) such that \(V\big(L_{t,k}\big)\cap V\left(C^{(0)}_k\right)=\{u_0\}\) and \(V\big(L_{s,k}\big)\cap V\left(C^{(0)}_k\right)=\{w_0\}\), where \(s\geq t\geq 1\). Suppose that \(C^{(t)}_k=u_1u_2\cdots u_ku_1\) and \(C^{(s)}_k=w_1w_2\cdots w_kw_1\) are the pendent polygons of \(L_{t,k}\) and \(L_{s,k}\), respectively, such that \(u_1\) and \(w_1\) are two cut-vertices of \(G\). Let \(G’=G-u_1u_2-u_1u_k+w_2u_2+w_2u_k\). By the definition of \(G’\), it it easy to see that
Observation 1. If \(t\geq 2\), then \(C^{(0)}_k\) is also a special polygon of \(G’\) and that \(L_{t-1,k}\) and \(L_{s+1,k}\) are two pendent cactus chains of \(G’\) such that \(V\big(L_{t-1,k}\big)\cap V\left(C^{(0)}_k\right)=\{u_0\}\) and \(V\big(L_{s+1,k}\big)\cap V\left(C^{(0)}_k\right)=\{w_0\}\). We consider all cases as follows, by the definition of \(G’\), we have
Apparently, if \(t\geq 2\), by observation 1 we can conclude that there exists a cactus \(G’\) of \(\mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G)=R_{\alpha}^{0}(G’)\), where \(C^{(0)}_k\) is also a special polygon of \(G’\) such that \(L_{t-1,k}\) and \(L_{s+1,k}\) are two pendent cactus chains of \(G’\), \(V\big(L_{t-1,k}\big)\cap V\left(C^{(0)}_k\right)=\{u_0\}\) and \(V\big(L_{s+1,k}\big)\cap V\left(C^{(0)}_k\right)=\{w_0\}\). By repeating the above process, we can also conclude that there exists a cactus \(G_1\) of \(\mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G)=R_{\alpha}^{0}(G_1)\), where \(C^{(0)}_k\) is also a special polygon of \(G_1\) such that \(L_{1,k}\) and \(L_{s+t-1,k}\) are two pendent cactus chains of \(G_1\), \(V\big(L_{1,k}\big)\cap V\left(C^{(0)}_k\right)=\{u_0\}\) and \(V\big(L_{s+t-1,k}\big)\cap V\left(C^{(0)}_k\right)=\{w_0\}\). And now for \(t=1\), through the operation illustrated before and (1), we can construct the corresponding graph \(G_2\) such that \(G_2\in \mathcal{G}_{n,k}\), \(R_{\alpha}^{0}(G)=R_{\alpha}^{0}(G_2)\) and one pendent chain will disappear in \(G_2\).
By repeating the above arguments, we can conclude that there exists \(G_0\in \mathcal{G}_{n,k}\) such that \(R_{\alpha}^{0}(G_0)\leq R_{\alpha}^{0}(G)\) for \(\alpha1\) and \(R_{\alpha}^{0}(G_0)\geq R_{\alpha}^{0}(G)\) for \(0< \alpha< 1\) and \(G_0\) contains no special polygon for \(k\geq 3\). Thus, the result holds.
Lemma 2.6. [7] Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\), where \(k\geq 3\) and \(n\geq 3\). If \(G\) contains neither singular vertex nor special polygon, then \(G\) must be a cactus chain.
Lemma 2.7. Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\). If \(k\geq 3\) and \(n\geq 3\), then \(R_{\alpha}^{0}(G)\leq \Psi(n,k,\alpha)\) for \(\alpha1\) and \(R_{\alpha}^{0}(G)\geq \Psi(n,k,\alpha)\) for \(0< \alpha< 1\), where either equality holds if and only if \(G \cong W_{n,k}\).
Proof. Let \(G\) be a cactus of \(\mathcal{G}_{n,k}\) such that \(G\) is an extremal graph of \(\mathcal{G}_{n,k}\), namely, \(R_{\alpha}^{0}(G)\) is as large as possible for \(\alpha1\), and \(R_{\alpha}^{0}(G)\) is as small as possible for \(0< \alpha< 1 \). We suppose that the degree of vertex \(u_{0}\) is largest among all vertices in \(G\) and \(d_{G}(u_{0})=2r_{1}\). If \(2r_{1}=2n\), then \(G\cong W_{n,k}\), and hence the result already holds. Otherwise, \(2r_{1}< 2n \). Furthermore, we suppose that \(C_{k}^{(1)}\) is a pendent polygon with \(u_{1}\) being its cut-vertex such that \(N(u_{1})\cap V(C_{k}^{(1)})=\{w_{1},w_{k}\}\) and \(d_{G}(u_{1})=2r_{2}\), where \(u_{1}\neq u_0\). Then it is easy to see that \(2\leq r_{2}\leq r_{1}\leq n\). Now, we let \(G_{1}=G-u_1w_1-u_1w_k+u_0w_1+u_0w_k\). By an elementary computation, it follows that \begin{align*}R_{\alpha}^{0}(G)-R_{\alpha}^{0}(G_1)&=(2r_1)^{\alpha}+(2r_2)^{\alpha}-(2r_1+2)^{\alpha}-(2r_2-2)^{\alpha} \\&=\left(2r_2\right)^{\alpha}-\left(2r_2-2\right)^{\alpha}-\big((2r_1+2)^{\alpha}-(2r_1)^{\alpha}\big).\end{align*} Since \(2r_1\geq2r_2\geq4\), by lemma 2.1 we have \(R_{\alpha}^{0}(G)< R_{\alpha}^{0}(G_1)\) for \(\alpha1\), and \(R_{\alpha}^{0}(G)>R_{\alpha}^{0}(G_1)\) for \(0< \alpha< 1\), which is contrary with the choice of \(G\). Thus, \(u_0\) is the cut-vertex of any pendent polygon. Since \(G\) is a cactus in \(\mathcal{G}_{n,k}\), we have \(G\cong W_{n,k}.\)
Next, we turn to prove Theorem 1.1.Proof. By Lemma 2.2, \(R_{\alpha}^{0}(G)=\Phi(n,k,\alpha)\) holds for \(G\in \mathcal{T}_{n,k}\), and \(R_{\alpha}^{0}(G)=\Psi(n,k,\alpha)\) holds for \(G\cong W_{n,k}\). Now, we consider the following two cases:
Case 1. \(\alpha1\).
Then, Lemmas 2.4–2.6 imply that \(R_{\alpha}^{0}(G)\) is minimum if \(G\in \mathcal{T}_{n,k}\). Combining this with Lemma 2.7, we can conclude that \(R_{\alpha}^{0}(G)\) is maximum if and only if \(G\cong W_{n,k}\). Thus, \((i)\) holds.
Case 1. \(0< \alpha< 1\).
By Lemmas 2.4–2.6, \(R_{\alpha}^{0}(G)\) is maximum if \(G\in \mathcal{T}_{n,k}\). Taking Lemma 2.7 into consideration, we can conclude that \(R_{\alpha}^{0}(G)\) is minimum if and only if \(G\cong W_{n,k}\). Thus, \((ii)\) also holds.