A \(k\)-plane tree is a tree drawn in the plane such that the vertices are labeled by integers in the set \(\{1,2,\ldots,k\}\), the children of all vertices are ordered, and if \((i,j)\) is an edge in the tree, where \(i\) and \(j\) are labels of adjacent vertices in the tree, then \(i+j\leq k+1\). In this paper, we construct bijections between these trees and the sets of \(k\)-noncrossing increasing trees, locally oriented \((k-1)\)-noncrossing trees, Dyck paths, and some restricted lattice paths.
Plane trees (or ordered trees) have computer science and mathematics applications alike. These are rooted trees with the property that all the children of the vertices are ordered. These trees have been generalized by labeling the vertices to obtain \(k\)-plane trees, which we now define. When the vertices of the plane trees are labeled with integers in the set \(\{1,2,\ldots,k\}\) such that there are no edges \((i,j)\) with the property that \(i+j>k+1\) then such trees are called \(k\)-plane trees. These trees were introduced and studied by Gu, Prodinger, and Wagner in [1]. The aforementioned authors showed that the number of \(k\)-plane trees with root labelled by \(h\) on \(n>1\) vertices is given by
Setting \(k=2\) and \(h=2\) in Eq. (1), we find that the number of \(2\)-plane trees on \(n\) vertices whose root is labelled by 2 is given by
\[\frac{1}{2n-1} \binom{3n-3}{n-1}.\] This formula also counts the number of noncrossing trees on \(n\) vertices and ternary trees on \(n-1\) vertices among other structures, see sequence https://oeis.org/A001764 in [3]. A bijection between the set of 2-plane trees and the set of ternary trees was constructed by Gu and Prodinger in an earlier paper [4]. Of course, setting \(k=h=1\) in Eq. (1), we recover Catalan’s number that counts the number of plane trees with \(n\) vertices.A \(k\)-noncrossing tree is a noncrossing tree whose vertices are labelled with integers in the set \(\{1,2,\ldots,k\}\) such that if an edge \((i,j)\) is an ascent in the path from the root then \(i+j\leq k+1\). These trees were first studied by Pang and Lv [5]. When \(k=2\) we obtain \(2\)-noncrossing trees, introduced and enumerated by Yan and Liu [6]. The author recently refined the formula of Yan and Liu in [7]. Similarly, when \(k=1\) we recover noncrossing trees.
In 2015, Okoth and Wagner [8] obtained counting formulas for the number of noncrossing trees whose edges are locally oriented. By local orientation, we mean that the edges are oriented from vertices of the lower label towards vertices of the higher label. The said authors coined the words locally-oriented noncrossing trees for these trees. In the same paper, they called a vertex of in-degree 0 (resp. outdegree 0) as source (resp. sink). A \(k\)-noncrossing tree whose edges have local orientation will be referred to as locally-oriented \(k\)-noncrossing tree.
A noncrossing increasing tree [9] is a noncrossing tree whose labels increase along the paths from the root of the tree. The number of these trees on \(n\) vertices is also given by the Catalan number \[\dfrac{1}{n}{2n-2\choose n-1}.\] In [10], Okoth introduced and enumerated 2-noncrossing increasing trees by root degree and the number of vertices labeled by 2. These are 2-noncrossing trees whose labels increase as one moves away from the root. In the same spirit, a \(k\)-noncrossing increasing tree is a \(k\)-noncrossing tree whose labels increase as one moves away from the root.
Lattice paths have been studied for centuries. For example, a Dyck path of length \(n\) is a path from point \((0,0)\) to point \((n,0)\) which consists of up steps and down steps such that the path does not go below the \(x\)-axis. In this paper, we also consider lattice paths starting at \((0,0)\) and consisting of unit vertical and unit horizontal steps such that the path either touches or lies above the line \(x=ky.\) We shall call these lattice paths as restricted lattice paths.
This paper is organized as follows: We construct bijections between the set of \(k\)-plane trees and the set of \(k\)-noncrossing increasing trees in §2, locally oriented \((k-1)\)-noncrossing trees in §3, Dyck paths in §4 and restricted lattice paths in §5 respectively. We conclude the paper in §6 and expose some problems.
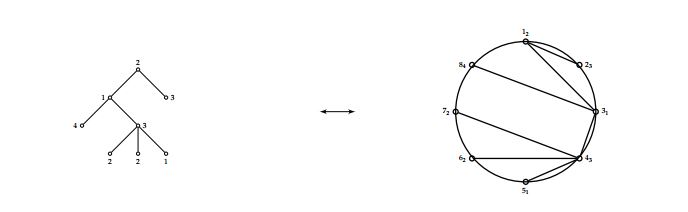
Theorem 1. There is a bijection between the set of \(k\)-plane trees on \(n\) vertices whose root is labelled by \(h\) and the set of \(k\)-noncrossing increasing trees on \(n\) vertices whose root is labelled by \(h\).
Proof. Let \(T\) be a \(k\)-plane tree on \(n\) vertices whose root is labeled by \(h\). We obtain a corresponding \(k\)-noncrossing increasing tree \(T’\) on \(n\) vertices whose root is labelled by \(h\) as follows: Each vertex in \(T\) becomes a vertex of \(T’\) and the children of a given vertex in \(T\) become right wing of a butterfly rooted at a corresponding vertex in \(T’\) such that if \(v_1, v_2,\ldots,v_i\) are the left-to-right children of the root \(v\) in \(T\) then \(v_1\) receives the highest label, followed by \(v_2\), and so on in \(T’\). Vertex \(v_i\) receives the least label. If a vertex is labeled by \(j\) in plane tree \(T\), the corresponding vertex in the noncrossing tree \(T’\) is labeled by \(j\). Therefore, the root of the \(k\)-noncrossing increasing tree is labeled by \(h\).
We now obtain the reverse procedure: Let \(T’\) be a \(k\)-noncrossing increasing tree with root \(r\) labeled by \(h\) and have \(n\) vertices. Let \(r_{1}< r_{2}< \cdots< r_{d}\) be the vertices of \(T'\) incident to \(r\). Vertex \(r\) corresponds to the root in the \(k\)-plane tree \(T\) and vertices \(r_{1},r_{2},\ldots, r_{d}\) corresp ond to the right-to-left children of the root in the \(k\)-plane tree. (So if the root in the \(k\)-noncrossing increasing tree is labeled by \(h\), the corresponding \(k\)-plane tree has its root labeled by \(h\).) Now, consider vertex \(r_1\) and all the vertices incident to it apart from \(r\), which is already in the \(k\)-plane tree. Draw these vertices as the children of \(r_1\). Again the ordering of the children is done with the vertex, with the largest label being the leftmost vertex. We repeat the process, and the algorithm stops when all the vertices have been drawn in the \(k\)-plane tree.
An example is given in Figure 1.
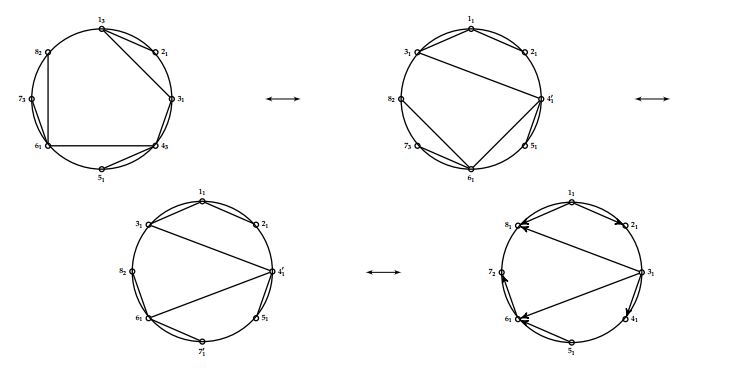
Theorem 2. There is a bijection between the set of \(k\)-plane trees with root labelled by \(k\) on \(n\) vertices, \(v_i\) of which are labelled by \(i\) for \(1\leq i\leq k\), and the set of locally oriented \((k-1)\)-noncrossing trees with root labelled by 1 on \(n\) vertices such that the total number of sources labelled by 1 is \(v_k\), non-source vertices labelled by 1 is \(v_1\) and for \(i\in\{1,2,\ldots,k-1\}\), there are \(v_i\) vertices labelled by \(i\).
Proof. By Theorem 1, it suffices to construct a bijection between the set of \(k\)-noncrossing increasing trees with root labelled by \(k\) on \(n\) vertices, \(v_i\) of which are labelled by \(i\) for \(1\leq i\leq k\), and the set of locally oriented \((k-1)\)-noncrossing trees with root labelled by 1 on \(n\) vertices such that the total number of sources labelled by 1 is \(v_k\), non-source vertices labelled by 1 is \(v_1\) and for \(i\in\{1,2,\ldots,k-1\}\), there are \(v_i\) vertices labelled by \(i\).
Consider a \(k\)-noncrossing increasing tree on \(n\) vertices with root labelled by \(k\). For \(i\in\{1,2,\ldots,k\}\), let the number of vertices labelled by \(i\) be \(v_i\). We obtain the corresponding locally oriented \((k-1)\)-noncrossing tree by the following steps:
We now obtain the reverse procedure:
For an example of the bijection, see Figure 2.
Setting \(k=2\) in Eq. (2), we recover the formula for the number of locally oriented noncrossing trees on \(n\) vertices with \(i\) sources obtained by Okoth and Wagner in [8]. In [7], the present author obtained the number of locally oriented \(2\)-noncrossing trees on \(n\) vertices whose root is labeled by 2 with a given number of vertices labeled by 2 and number of sources labeled by 1.
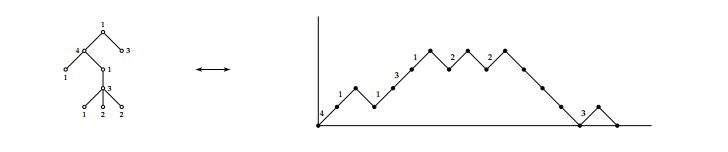
Let \(T\) be a \(k\)-plane tree with root labeled by 1 on \(n\) vertices. We obtain the Dyck path \(D\) of length \(2n-2\) as follows: Starting to the left of a given plane tree \(T\), we move around the tree, always moving away from the root on the left-hand side of an edge and moving towards the root on the right-hand side of an edge. Each edge corresponds to one-up step and one down step is as follows:
For a bijection, we obtain the reverse procedure: Let \(D\) be a Dyck path of length \(2n-2\) such that its up steps are labelled with integers in the set \(\{1,2,\ldots,k\}\) and that label \(i\) is never followed by label \(j\) if \(i+j>k+1.\) We obtain a corresponding \(k\)-plane tree with a root labeled by 1 on \(n\) vertices by the following procedure: Draw a vertex \(v\) and label it 1. Starting at the beginning of the Dyck path, if the up step is labeled \(i\) then draw an edge connecting \(v\) to a new vertex labeled by \(i\). Continue the process with the Dyck path until you get a down step. For each down step, move up an edge (on the right-hand side of the edge, in the tree already drawn, towards the root). Continue until you find an up step. Let \(u\) be the vertex reached before the up step. If the up step is labeled \(j\) then draw an edge connecting \(u\) to a new vertex labeled by \(j\). Repeat the procedure until all paths in the Dyck path are visited. The tree obtained is a \(k\)-plane tree with roots labeled by 1 on \(n\) vertices.
Figure 3 below gives an example of the bijection.
Based on the bijection above, we give the following theorem:
Theorem 3. The number of Dyck paths from \((0,0)\) to \((2n-2,0)\), consisting of \((n-1)\) down steps of unit length and \((n-1)\) up steps of unit length labelled by integers in the set \(\{1,2,\ldots,k\}\) such that if label \(i\) is followed by label \(j\) then \(i+j\leq k+1\), is given by \begin{align*} \dfrac{1}{n}{(k+1)n-2\choose n-1}. \end{align*}
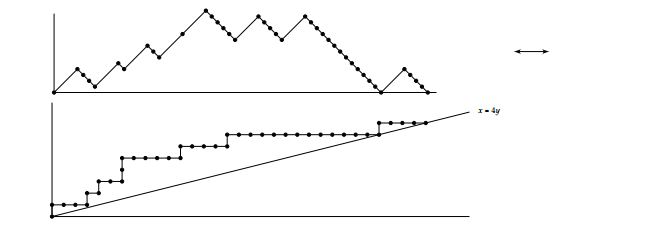
We note that the case of \(k=2\) in Theorem 3 was obtained in [10] and of \(k=1\) gives the equivalent result for unlabelled Dyck paths, given by Catalan numbers.Let \(T\) be a \(k\)-plane tree with root labelled by \(1\) on \(n\) vertices. We obtain the corresponding lattice path with \(n-1\) vertical steps and \(kn-k\) horizontal steps such that the paths never go below the line \(x=ky\). We use the procedure of Gu, Prodinger and Wagner in [1] to move from a \(k\)-plane tree to a Dyck path. We shall then construct a bijection beween the set of the Dyck paths and the set of the lattice paths defined here. Before we present our bijection and for the benefit of clarity, we present the bijection obtained by the said authors in the next subsection.
Let us now obtain the reverse procedure: Let \(D\) be a Dyck path from \((0,0)\) to \((2kn-2k,0)\). We obtain a corresponding \(k\)-plane tree on \(n\) vertices whose root is labelled by \(k\) by the following procedure: We visit all up steps and down steps of the Dyck path starting at point \((0,0)\).
An example to explain the bijection is given in Figure 4.

We obtain the reverse procedure: Let \(L\) be a lattice path comprising of \(n-1\) unit vertical steps and \(kn-k\) unit horizontal steps such that the lattice path lies above or touches the line \(x=ky\). We obtain its corresponding Dyck path as follows:
An example is given in Figure 5 which corresponds to the 4-plane tree and Dyck path in the last subsection.