A \(2\)-noncrossing tree is a rooted tree drawn in the plane with its vertices (colored black or white) on the boundary of a circle such that the edges are line segments that do not intersect inside the circle and there is no black-black ascent in any path from the root. A rooted tree is said to be increasing if the labels of the vertices are increasing as one moves away from the root. In this paper, we use generating functions and bijections to enumerate \(2\)-noncrossing increasing trees by the number of blacks vertices and by root degree. Bijections with noncrossing trees, ternary trees, 2-plane trees, certain Dyck paths, and certain restricted lattice paths are established.
Trees (or mathematical trees) have been studied for centuries. These include Cayley trees, binary trees, plane trees, \(d\)-ary trees, noncrossing trees among many others. In the last two decades, these trees have been generalized by colouring the vertices.
When the vertices of the plane trees are labeled with integers in the set \(\{1,2,\ldots,k\}\) such that there are no edges \((i,j)\) with the property that \(i+j>k+1\) then such trees are called \(k\)-plane trees. These trees were introduced and studied by Gu, Prodinger and Wagner in [1]. In an earlier paper [2], Gu and Prodinger constructed a bijection between the set of \(2\)-plane trees and the set of ternary trees. These structures are counted by the same formula that counts noncrossing trees.
In 2010, Pang and Lv [3] introduced \(k\)-noncrossing trees. These are trees drawn in the plane with vertices on the boundary of a circle and edges are line segments that do not cross inside the circle and the vertices are labeled with integers in the set \(\{1,2,\ldots,k\}\) such that if an edge \((i,j)\) is an ascent in the path from the root then \(i+j\leq k+1\). When \(k=2\) we obtain \(2\)-noncrossing trees, introduced and enumerated by Yan and Liu [4] and further studied by Okoth [5]. Similarly, when \(k=1\) we get noncrossing trees extensively studied in the literature. See [6-9] among other papers.
In 2015, Okoth and Wagner [10] enumerated noncrossing trees whose edges are oriented from vertices of lower labels towards vertices of higher labels. These trees are called locally oriented noncrossing trees or simply lnc-trees therein. In the same paper, a source is a vertex of indegree 0 and a sink is a vertex of outdegree 0. In 2021, Okoth [5] enumerated 2-noncrossing trees according to the number of vertices of label 2 and the number of non-source vertices of label 1. For the rest of the paper, a vertex of label 2 will be called a black vertex and a vertex of label 1 will be referred to as a white vertex.
A noncrossing increasing tree [6] is a noncrossing tree whose labels are increasing if we consider a path from the root. These trees are counted by the famous Catalan number [6]. In the present paper, we enumerate 2-noncrossing increasing trees which are 2-noncrossing trees with increasing labels along paths from the root (vertex 1). All the structures described above are enumerated by Catalan-like formulas.
This paper is organized as follows: Formulas that count the number of 2-noncrossing increasing trees according to the number of black vertices and root degree are obtained in Section 2. The formula that counts the number of 2-noncrossing increasing trees with a black root according to the number of black vertices also counts the number of locally oriented noncrossing trees on \(n\) vertices, \(k\) of which are sources, and ternary trees on \(n-1\) vertices and having \(k\) right-edges as well as 2-plane trees with a black root on \(n\) vertices, \(k\) of which are black. These bijections are presented in Section 3. In the same spirit, the formula that counts the number of 2-noncrossing increasing trees with a white root also enumerates certain Dyck paths and certain restricted lattice paths. These bijections are established in Section 4.
Theorem 1. The number of 2-noncrossing increasing trees with a black root on \(n\) vertices, \(k\) of which are black, is given by \[\begin{aligned} \label{exactly_black} \dfrac{1}{n-1}{2n-2\choose n-k-1}{n-1\choose k-1}. \end{aligned} \tag{1}\]
Proof. Let \(T(z)\) and \(S(z)\) be the generating functions for the number of 2-noncrossing trees with black and white roots respectively. According to [5], these generating functions satisfy the functional equations: \[\begin{aligned} T=\dfrac{z}{1-\frac{S^2}{z}} \end{aligned}\] and \[\begin{aligned} S=\dfrac{z}{1-\left(\frac{S^2}{z}+\frac{ST}{z}\right)}. \end{aligned}\] Let \(v\) mark the number of black vertices in the 2-noncrossing increasing tree. Again as in [5], we will now distinguish two types of \(2\)-noncrossing trees with a white root:
Type 1: root has lowest label
Type 2: root has highest label
Let \(S_1\) and \(S_2\) be the generating functions of 2-noncrossing trees with white roots of Types 1 and 2 respectively. Considering the decomposition of 2-noncrossing trees with a black root we get
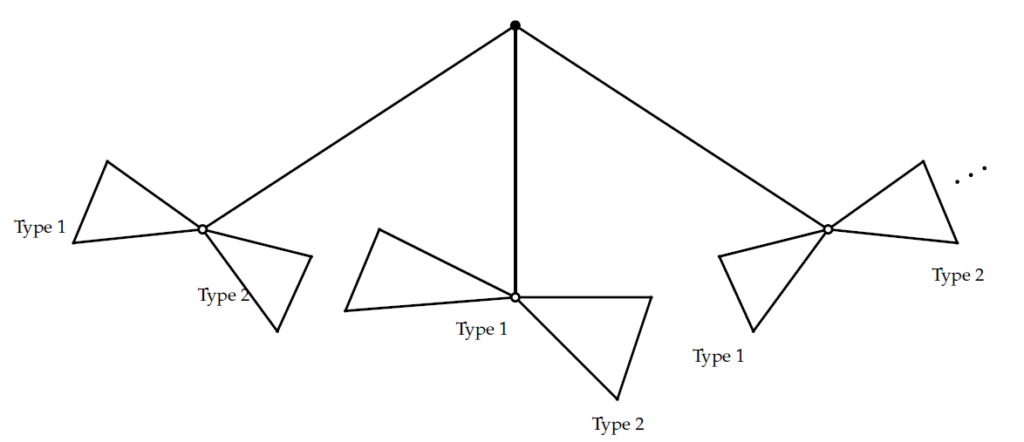
We have one additional black vertex (the root). So we get
\[\begin{aligned} T=\dfrac{zv}{1-\frac{S_1S_2}{z}}. \end{aligned}\] Lets now consider 2-noncrossing trees with a white root: For those trees of Type 1, the decomposition is
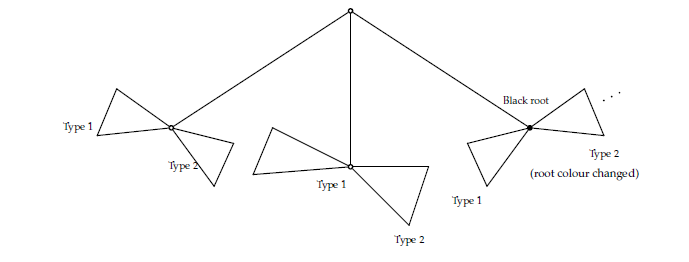
Here, there are two types of butterflies which correspond to \(\frac{S_1S_2}{z}\) and \(\frac{S_2T}{z}\) respectively. Each black vertex must already occur in one of the smaller trees of the decomposition. So we get, \[\begin{aligned} S_1=\dfrac{z}{1-\left(\frac{S_1S_2}{z}+\frac{S_2T}{z}\right)}. \end{aligned}\] Let \(T_I\) and \(S_I\) be the generating functions for 2-noncrossing increasing trees with black and white roots respectively. Since in 2-noncrossing increasing trees, there are no right butterflies, we set \(S_2=z\), \(S_1=S_I\) and \(T=T_I\) to obtain \[\begin{aligned} T_I=\dfrac{zv}{1-S_I} \end{aligned}\] and \[\begin{aligned} \label{eq1} S_I=\dfrac{z}{1-S_I-T_I} \end{aligned} \tag{2}\] Let \[\begin{aligned} \label{Y} T_I=zv(1+Y). \end{aligned} \tag{3}\] It follows that \[\begin{aligned} T_I=\dfrac{zv}{1-S_I} \end{aligned}\] and \[\begin{aligned} \label{eq2} 1-S_I=\dfrac{zv}{T_I}=\dfrac{1}{1+Y} \end{aligned} \tag{4}\] so that \[\begin{aligned} \label{eq4} S_I=\dfrac{zv}{T_I}=\dfrac{Y}{1+Y}. \end{aligned} \tag{5}\] Thus, \[\begin{aligned} \label{eq3} \dfrac{Y}{S_I(1+Y)}=1. \end{aligned} \tag{6}\] From Equations (2) and (4), we have \[\begin{aligned} S_I=\dfrac{z}{\dfrac{1}{1+Y}-vz(1+Y)}. \end{aligned}\] Using Equation (6), we get \[\begin{aligned} S_I&=\dfrac{z}{\dfrac{1}{1+Y}- \dfrac{vzY}{S_I}}\\ &=\dfrac{zS_I(1+Y)}{S_I-vzY(1+Y)}. \end{aligned}\] So, \[\begin{aligned} S_I-vzY(1+Y)=z(1+Y). \end{aligned}\] Thus \[\begin{aligned} \label{white} \nonumber S_I&=z(1+Y)+vzY(1+Y)\\ &=z(1+Y)(1+vY). \end{aligned} \tag{7}\] From Equation (5), we get \[\begin{aligned} \dfrac{Y}{1+Y}=z(1+Y)(1+vY) \end{aligned}\] so that \[\begin{aligned} \label{Y1} Y=z(1+Y)^2(1+vY). \end{aligned} \tag{8}\] This functional equation is in the form we can apply Lagrange Inversion Formula [11]. We now extract the coefficient of \(z^nv^k\) in \(T_I.\) \[\begin{aligned} T_I&=[z^{n-1}v^{k-1}](1+Y)=[z^{n-1}v^{k-1}]Y\\&= \dfrac{1}{n-1}[y^{n-2}v^{k-1}]((1+y)^2(1+vy))^{n-1}\\ &= \dfrac{1}{n-1}[y^{n-2}v^{k-1}](1+y)^{2n-2}(1+vy)^{n-1}\\ &= \dfrac{1}{n-1}[y^{n-2}v^{k-1}]\sum_{i\geq 0} \sum_{j\geq 0}{2n-2\choose i}y^i{n-1\choose j}v^jy^j\\ &= \dfrac{1}{n-1}[y^{n-2}v^{k-1}]\sum_{i\geq 0} \sum_{j\geq 0}{2n-2\choose i}{n-1\choose j}v^jy^{i+j}\\ &= \dfrac{1}{n-1}[y^{n-2}]\sum_{i\geq 0} {2n-2\choose i}{n-1\choose k-1}y^{i+k-1}\\ &= \dfrac{1}{n-1} {2n-2\choose n-k-1}{n-1\choose k-1}. \end{aligned}\] This completes the proof. ◻
Corollary 2. There are a total of \[\begin{aligned} \label{increasing_black} \dfrac{1}{n-1}{3n-3\choose n-2} \end{aligned} \tag{9}\] 2-noncrossing increasing trees with a black root on \(n\) vertices.
Proof. We sum over all \(k\) in Equation (1), making use of Vandermonde’s Convolution Formula, to obtain the required formula. ◻
Corollary 3. The mean and variance of the number of black vertices in 2-noncrossing increasing trees on \(n\) vertices with a black root are equal to \((n+1)/3\) and \((4n^2-10n+4)/(27n-36)\) respectively.
Proof. From Equations (1) and (9), we find that the proportion of all 2-noncrossing trees with black roots on \(n\) vertices which have \(k\) black vertices is given by \[\begin{aligned} \label{total_k} \dfrac{{n-1\choose k-1}{2n-2\choose n-k-1}}{{3n-3\choose n-2}}. \end{aligned} \tag{10}\] Multiplying Equation (10) by \(k\) and summing over all \(k\), we obtain the mean. For variance, we multiply Equation (10) by \(k^2\) and sum over all \(k\). The square of the mean is then substracted. ◻
Remark 1. We remark that Equation (1) counts the number of noncrossing trees on \(n\) vertices with \(k\) sources as well as the number of ternary trees on \(n-1\) vertices with \(k\) right-edges. Bijections with these structures are presented in Section 3.
Theorem 4. The number of 2-noncrossing increasing trees on \(n\) vertices with a white root such that there are \(k\) black vertices is given by \[\begin{aligned} \label{exactly_white} \frac{1}{2n-1}{n-1\choose k}{2n-1\choose n-k}. \end{aligned} \tag{11}\]
Proof. 2-noncrossing increasing trees with a white root has the generating function \(S_I\), given in the proof of Theorem 1. From Equation (7), we have that \(S_I=z(1+Y)(1+vY)\) where \(Y\) satisfies the functional equation \(Y=z(1+Y)^2(1+vY)\). As before, \(v\) marks the number of black vertices. We have, \[\begin{aligned} \label{S_1_white} \nonumber [z^n]S_I&=[z^{n-1}](1+vY+Y+vY^2)\\ &=v[z^{n-1}]Y+[z^{n-1}]Y+v[z^{n-1}]Y^2. \end{aligned} \tag{12}\] By Lagrange inversion we have, \[\begin{aligned} \label{first_part} v[z^{n-1}]Y &=\frac{1}{n-1}\sum_{k\geq 1}{n-1\choose k-1}v^{k}{2n-2\choose n-k-1}. \end{aligned} \tag{13}\] We also have \[\begin{aligned} \label{second_part} [z^{n-1}]Y&=\frac{1}{n-1}\sum_{k\geq 0} {n-1\choose k}v^{k}{2n-2\choose n-k-2} \end{aligned} \tag{14}\] and \[\begin{aligned} \label{third_part} v[z^{n-1}]Y^2&=\frac{2}{n-1}\sum_{k\geq 1}{n-1\choose k-1} v^{k}{2n-2\choose n-k-2}. \end{aligned} \tag{15}\] Now, from Equations (12),(13),(14) and (15), we have that the number of 2-noncrossing increasing trees with a white root and \(n\) vertices, \(k\) of which are black is given by \[\begin{aligned} S_I&=\frac{1}{n-1}{n-1\choose k-1}{2n-2\choose n-k-1}+\frac{1}{n-1}{n-1\choose k}{2n-2\choose n-k-2}+\frac{2}{n-1}{n-1\choose k-1}{2n-2\choose n-k-2}. \end{aligned}\] After simple algebraic manipulations we obtain \[\begin{aligned} S_I&=\frac{1}{2n-1}{n-1\choose k}{2n-1\choose n-k}. \end{aligned}\] This is the desired result. ◻
Corollary 5. There are a total of \[\begin{aligned} \label{increasing_white} \dfrac{1}{2n-1}{3n-2\choose n} \end{aligned} \tag{16}\] 2-noncrossing increasing trees with a white root on \(n\) vertices.
Proof. We sum over all \(k\) in Equation (1) to obtain the required formula. ◻
Corollary 6. The mean and variance of the number of black vertices in 2-noncrossing increasing trees on \(n\) vertices with a white root are equal to \((n^2-n)/(3n-2)\) and \((4n^3-6n^2+2n)/(27n^2-36n+12)\) respectively.
Proof. From Equations (11) and (16), we find that the probability of a 2-noncrossing tree with a white root on \(n\) vertices to have \(k\) black vertices is given by \[\begin{aligned} \label{total_k_white} \dfrac{{n-1\choose k}{2n-1\choose n-k}}{{3n-2\choose n}}. \end{aligned} \tag{17}\] Now multiplying Equation (17) by \(k\) and summing over all \(k\), we obtain the mean. To obtain variance, we multiply Equation (17) by \(k^2\) and sum over all \(k\). We then subtract square of the mean. ◻
Summing Equations (9) and (16), we find that there are \[\begin{aligned} \dfrac{1}{n-1}{3n-3\choose n} \end{aligned}\] \(2\)-noncrossing increasing trees on \(n\) vertices.
Remark 2. We remark that Equation (16) counts the number of some Dyck paths and some restricted lattice paths among other structures. Bijections with these Dyck paths and lattice paths are presented in Section 4.
Let \(T(z)=\sum_{n=0}^{\infty}T_nz^n\) and \(S(z)=\sum_{n=0}^{\infty}S_nz^n\) be the generating functions for \(2\)-noncrossing trees with black and white roots respectively. Let \(t(n,d)\) be the number of \(2\)-noncrossing trees of order \(n\) such that vertex 1 is a black root and is of degree \(d\). The following lemma expresses \(t(n,d)\) as a convolution on the numbers \(S_n\) of \(2\)-noncrossing trees on \(n\) vertices such that the root is white.
Lemma 7. The numbers \(t(n,d)\) can be written in terms of the numbers \(S_n\) as follows: \[\begin{aligned} t(n,d)=\sum_{\substack{i_1+i_2+\cdots+i_{2d}=n+d-1 \\ i_1,i_2,\ldots,i_{2d}\geq 1 }}S_{i_1}S_{i_2}\cdots S_{i_{2d}}. \end{aligned}\]
Proof. Let \(T\) be a \(2\)-noncrossing tree on \(n\) vertices with a black root of degree \(d\) and is joined to vertices \(v_{1}<v_{2}<\cdots< v_{d}\). By definition of \(2\)-noncrossing trees, these vertices must all be white. For every \(i=1,2,\ldots,d-1,\) the subgraph induced by \(T\) on the vertex set \(\{v_{i},\ldots, v_{{i+1}}\}\) is the disjoint union of two \(2\)-noncrossing trees with white roots. This produces a total of \(2d-2\) trees. Also, the subgraphs induced on \(\{2,\ldots, v_{{1}}\}\) and \(\{v_{d},\ldots, n\}\) are both \(2\)-noncrossing trees with white roots. Therefore, there are \(2d\), \(2\)-noncrossing trees with white roots. Let these trees be on \(i_1,i_2,\cdots, i_{2d}\) vertices respectively. It can be checked that \(i_1+i_2+\cdots+i_{2d}=n+d-1\). Moreover, a family of \(2d\), \(2\)-noncrossing trees with white roots on the corresponding vertex set determines a unique \(2\)-noncrossing tree \(T\) with a black root. This proves the formula. ◻
The proof of the following theorem can be found in [12].
Theorem 8 (Lagrange-Bürmann). Let \(p(z)\) be a power series with complex coefficients and \(\lambda\) a complex number, satisfying an equation \[p(z)=\lambda+z\cdot h(p(z)).\] Then \[[z^n]g(p(z))=g(\lambda)+\dfrac{1}{n!}\dfrac{\mathrm{d}^{n-1}}{\mathrm{d}t^{n-1}}\left(\dfrac{\mathrm{d}}{\mathrm{d}t}(g(t))\cdot (h(t))^n\right)_{t=\lambda}.\]
We now state and prove the main result of this subsection.
Theorem 9. The number of 2-noncrossing increasing trees with a black root on \(n\) vertices such that the root has degree \(d\) is given by \[\begin{aligned} \label{root_degree} \dfrac{2d}{n-d-1}{3n-d-4\choose n-d-2}. \end{aligned} \tag{18}\]
Proof. Setting \(v=1\) in Equations (3) and (8), we find that the generating function \(T_I\) of 2-noncrossing increasing trees with a black root is given by \(T_I=z(1+Y)\) where \(Y=z(1+Y)^3\). Let \(B=1+Y\) so that \(T_I=zB\), \(Y=B-1\) and \(B=1+zB^3.\)
The convolution of Lemma 7 translates directly into the following equation: \[T_d=\dfrac{1}{z^{d-1}} T_I^{2d}=z^{d+1}B^{2d}\] where the coefficients in the series \(T_d\) give the number of 2-noncrossing trees with a black root of degree \(d\). Since \(B=1+zB^3\), apply Lagrange-Bürmann Inversion Formula (Theorem 8) to the series \(T_d\) with \(\lambda=1, h(t)=t^3\) and \(g(t)=t^{2d}\) to get \[\begin{aligned} B^{2d}&=\dfrac{1}{n!} \dfrac{d^{n-1}}{dt^{n-1}}\left\{2dt^{3n+2d-1}\right\}_{t=1}\\ &=\dfrac{2d}{n!}(3n+2d-1)(3n+2d-2)\cdots(2n+2d+1)\\ &=\dfrac{2d}{n!}\cdot \dfrac{(3n+2d-1)!}{(2n+2d)!}\\ &=\dfrac{2d}{n}{3n+2d-1\choose n-1}. \end{aligned}\] Therefore, \[\begin{aligned} T_d=[z^{n-d-1}]B^{2d}=\dfrac{2d}{n-d-1}{3n-d-4\choose n-d-2}. \end{aligned}\] This completes the proof. ◻
Setting \(d=1\) in Equation (18), we find that the number of \(2\)-noncrossing increasing tree with a black root on \(n\) vertices such that the root is of degree one is given by \[\begin{aligned} \dfrac{1}{n-1}{3n-5\choose n-2}. \end{aligned}\]
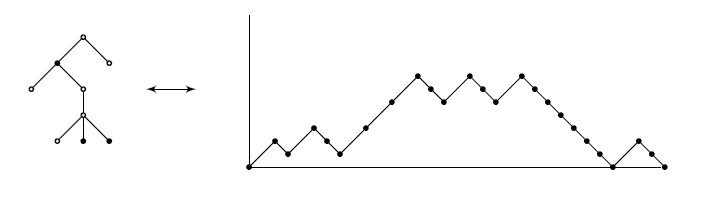
Theorem 10. There is a bijection between the set of 2-noncrossing increasing trees with a black root on \(n\) vertices, \(k\) of which are black and the set of locally oriented noncrossing trees on \(n\) vertices, \(k\) of which are sources.
Proof. Consider a \(2\)-noncrossing increasing tree with a black root on \(n\) vertices, \(k\) of which are black. We obtain a locally oriented noncrossing tree on \(n\) vertices, \(k\) of which are sources by the following steps. Recolour the root as white.
Starting at the root, we visit the vertices of the 2-noncrossing increasing tree in clockwise direction. Let \(v\) be the first black vertex (other than the root). Let \(u\) be the vertex incident to \(v\) such that \(u<v\). Vertex \(u\) is coloured white since there are no black-black edges. (See proof of Theorem 1).
Insert a new vertex \(v'\) just before \(u\). Delete the edge \(uv\) and create a new edge \(uv'\). Adjoin \(v\) and the butterflies rooted at \(v\) as the right wing of the butterfly rooted at \(v'.\) Colour \(v'\) as a white vertex.
Repeat the procedure until all the vertices are coloured white.
Rename the vertices in clockwise direction as \(1,2,\ldots,n\) and use local orientation to give directions to the edges. The tree obtained is a noncrossing tree on \(n\) vertices with \(k\) sources.
We now obtain the reverse procedure:
Recolour the root of the locally oriented noncrossing tree as black. Starting at the root, we visit the vertices of the locally oriented noncrossing tree in clockwise direction. Let \(v\) be the source with the largest label. Let \(u\) be the vertex incident to \(v\) such that \(u>v\) and \(u\) is the vertex with the largest label.
Insert a new vertex \(u'\) after \(v\). Delete the edge \(uv\) and create a new edge \(vu'\). Adjoin \(u\) and the butterflies rooted at \(u\) as the right wing of the butterfly rooted at \(u'.\) Colour \(u'\) as a black vertex.
Rename the vertices in clockwise direction as \(1,2,\ldots,n\).
Repeat the procedure until there is no white source. The tree obtained is a 2-noncrossing increasing tree on \(n\) vertices, \(k\) of which are black.
See Figure 2 for an example.

In [10], the present author and his coauthor constructed a bijection between the set of locally oriented trees with a given number of sources and sinks and the set of ternary trees with a given number of left-edges, middle-edges and right-edges. Precisely, the authors showed that \[\begin{aligned} \dfrac{1}{n-1}{n-1\choose k-1}{n-1\choose \ell-1}{n-1\choose n-k-\ell} \end{aligned}\] counts the number of locally oriented noncrossing trees on \(n\) vertices with \(k\) sources and \(\ell\) sinks as well as the number of ternary trees on \(n-1\) vertices such that there are \(k\) right-edges, \(\ell\) middle-edges and \(n-k-\ell\) left edges.
We can thus construct a ternary tree from a 2-noncsrossing increasing tree via a noncrossing tree and the following corollary follows:
Corollary 11. There is a bijection between the set of 2-noncrossing increasing trees on \(n\) vertices with \(k\) black vertices and the set of ternary trees on \(n-1\) vertices with \(k-1\) right edges.
Theorem 12. There is a bijection between the set of 2-noncrossing increasing trees with a black root on \(n\) vertices, \(k\) of which are black and the set of 2-plane trees on \(n\) vertices, \(k\) of which are black.
Proof. We construct a bijection between the set of 2-noncrossing increasing trees on \(n\) vertices with a black root and the set of \(2\)-plane trees on \(n\) vertices with a black root.
Let \(T\) be a \(2\)-noncrossing increasing tree with a black root \(v\) and having \(k\) black vertices (including the root) and a total of \(n\) vertices. Let \(v_{1}<v_{2}<\cdots< v_{d}\) be the vertices incident to \(v\). Vertex \(v\) corresponds to the root and vertices \(v_{1},v_{2},\ldots, v_{d}\) correspond to the right-to-left children of the root in the \(2\)-plane tree. Now, consider vertex \(v_1\) and all the vertices incident to it apart from \(v\) which is already in the 2-plane tree. Draw these vertices as the children of \(v_1\). Again the ordering of the children is done with the vertex with the least label being the rightmost vertex. We repeat the procedure stops when all the vertices have been drawn. Since all the black vertices in 2-noncrossing increasing remain black in 2-plane trees then we obtain a 2-plane tree with a black root with a black root on \(n\) vertices, \(k\) of which are black. This procedure is easily reversible.
An example is given in Figure 3.
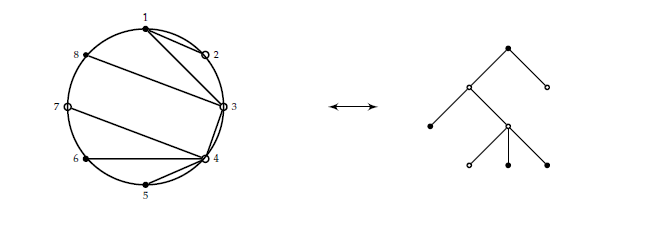
Corollary 13. The number of 2-noncrossing increasing trees with a black root on \(n\) vertices such that colours of the vertices alternate is given by the \((n-1)^{\text{th}}\) Catalan number \[\dfrac{1}{n}{2n-2\choose n-1}.\]
Proof. The proof follows since these 2-noncrossing trees are in bijection with plane trees such that all vertices at odd level are coloured white and all vertices at even level are coloured black. ◻
Remark 3. In the 2-noncrossing increasing tree \(T\) above, the root is black. It follows that the corresponding 2-plane tree is rooted at a black vertex. If \(T\) is a 2-noncrossing increasing tree with a white root then the corresponding 2-plane tree is rooted at a white vertex. This provides a bijective proof of Theorem 4.
In the online encyclopedia [13, A006013], David Scambler recorded that Equation (16) counts the number of Dyck paths of length \(2n-2\) such that the upsteps (\((1,1)\) steps) in the path are coloured in two ways \((B \text{ or } W)\) and avoiding \(BB.\) We now construct a bijection between the set of these paths of length \(2n-2\) and the set of 2-noncrossing increasing trees with a white root on \(n\) vertices. We construct the bijection via 2-plane trees with white roots described in Section 3.
Let \(T\) be a 2-noncrossing increasing tree on \(n\) vertices with a white root and \(T'\) its corresponding 2-plane tree with a white root on \(n\) vertices (See Subsection 3.2). We obtain the corresponding Dyck path of length \(2n-2\). Starting to the left of a given tree \(T\), we move around the tree (in preorder), always moving away from the root on the left hand side of an edge and moving towards the root on the right hand side of an edge. Each edge corresponds to one upstep and one downstep as follows:
Draw an upstep (coloured \(W\)) if the vertex visited, as one traverses an edge on the left hand side of the edge, is a white vertex.
Draw an upstep (coloured \(B\)) if the vertex visited, as one traverses an edge on the left hand side of the edge, is a black vertex.
Draw a downstep if one traverses an edge on the right hand side of the edge (towards the root).
We obtain a Dyck path of length \(2n-2\) with upsteps coloured in two ways \((B \text{ or } W)\) and avoiding \(BB.\)
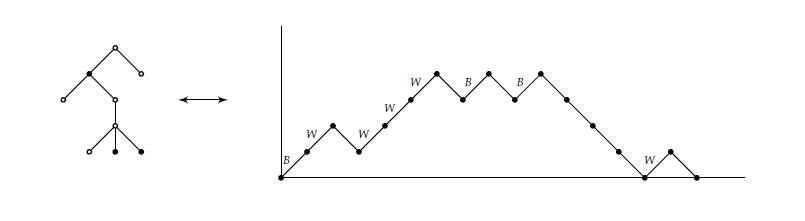
We now obtain the reverse procedure: Let \(D\) be a Dyck path of length \(2n-2\) such that its upsteps are coloured by either \(B\) or \(W\) colours such that \(B\) is never followed by a \(B\). We obtain a corresponding \(2\)-plane tree with a white root on \(n\) vertices as follows: Draw a vertex (call it \(r\)) and colour it white. Starting at the beginning of the Dyck path, if the upstep is coloured \(B\) (or \(W\)) then draw an edge connecting \(r\) to a new vertex coloured black (white respectively). Continue until you find a downstep. For each downstep, move up an edge (on the right hand side of the edge, in the tree already constructed, towards the root). Continue until you find an upstep. Let \(v\) be the vertex reached before the upstep. If the upstep is coloured \(B\) (or \(W\)) then draw an edge connecting \(v\) to a new vertex coloured black (white respectively). Repeat the procedure until all paths in the Dyck path are considered. We obtain a \(2\)-plane tree with a white root on \(n\) vertices.
The bijection is described in Figure 4.
In the aforementioned encyclopedia [13, A006013], combinatorialist Ira Gessel remarked that Equation (16), counts the number of lattice paths of with unit vertical steps (\(2n-2\) in total) and unit horizontal steps (\(n-1\) in total) such that the paths never go above the line \(y=2x\). We now construct a bijection between the set of these paths and the set of \(2\)-noncrossing increasing trees with a white root on \(n\) vertices. Again we construct the bijection via the 2-plane trees with white roots described in Subsection 3.2.
Let \(T\) be a \(2\)-noncrossing increasing tree on with a white root \(n\) vertices and \(T'\) be its corresponding \(2\)-plane tree with a white root on \(n\) vertices. We obtain the corresponding lattice path with \(2n-2\) steps vertical and \(n-1\) horizontal steps such that the paths never go above the line \(y=2x\). We move from 2-plane trees to the lattice paths via Dyck paths obtained by Gu, Prodinger and Wagner in [1]. For clarity of our bijection, we present their construction as well.
We first give the procedure of obtaining a Dyck path from a 2-plane tree. Starting to the left of a given tree \(T'\), we move around the tree (in preorder), always moving away from the root on the left hand side of an edge and towards the root on the right hand side of an edge. Each edge contributes a total of two steps as follows:
Draw an upstep (\((2,2)\) step) if the vertex visited, as one traverses an edge on the left hand side of the edge, is a white vertex.
Draw an upstep (\((2,2)\) step), followed by a downstep (\((1,-1)\) step) if the vertex visited, as one traverses an edge on the left hand side of the edge, is a black vertex.
Draw one downstep (\((1,-1)\) step)) or two downsteps (\((1,-1)\) steps) if one traverses an edge on the right hand side of the edge and the initial vertex is black or white respectively.
We obtain a Dyck path from \((0,0)\) to \((4n-4, 0).\)
We now obtain the reverse procedure: Let \(D\) be a Dyck path from \((0,0)\) to \((4n-4,0)\). We obtain a corresponding \(2\)-plane tree with a white root on \(n\) vertices as follows: Draw a vertex (call it \(r\)) and colour it white. Starting at the beginning of the Dyck path, if the upstep is followed by a downstep then draw an edge from \(r\) to new vertex \(v\) coloured black. If there is upstep which is not followed by a downstep then colour the new vertex \(v\) as white. If the final vertex in the tree is coloured white (or black) then for consecutive two downsteps (one dowstep respectively), move up the edge of the tree on the right hand side of the edge towards the root. Continue until you find the next upstep. Let \(w\) be the vertex reached before an upstep. If the upstep is followed by a dowstep then draw an edge from \(w\) to new vertex \(x\) coloured black. If there is an upstep which is not followed by a downstep then colour the new vertex \(x\) as white. We obtain a 2-plane tree with a white root on \(n\) vertices. The bijection is given in Figure 5.
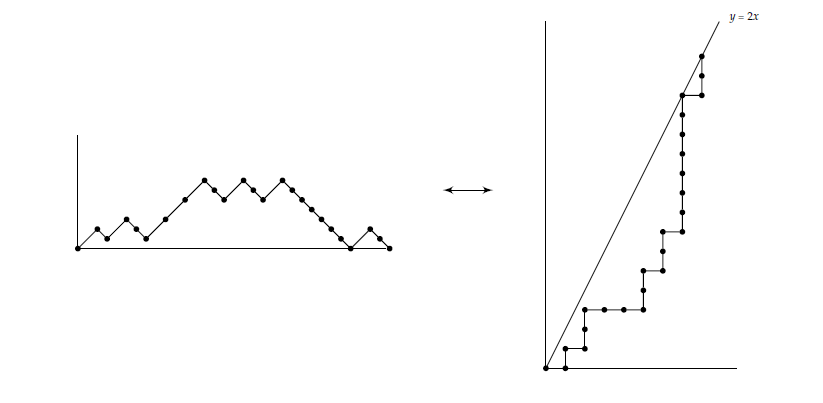
Let \(D\) be the Dyck path as in Subsection 4.2.1. We obtain a lattice path from \((0,0)\) to \((n-1, 2n-2)\) which does not go above the line \(y=2x\) and having \(n-1\) horizontal steps by the following steps.
For each upstep, draw a horizontal step.
For each downstep, draw a vertical step.
The lattice path obtained is either below or touches the line \(y=2x\).
We now obtain the reverse procedure: Let \(L\) be a lattice path of \(3n-3\) steps consisting of unit vertical steps and unit horizontal steps such that the lattice path lies below or touch the line \(y=2x\). We obtain a corresponding Dyck path as follows:
For each horizontal step, draw an upstep.
For each vertical step, draw a downstep.
An example is given in Figure 6.
Remark 4. The sequence \(1,2,7,30,\ldots\) for the number of \(2\)-noncrossing increasing trees with a white root is recorded as A006013 in Sloane’s celebrated online encyclopedia [13]. Some of the structures counted by this sequence are presented in this section in which their bijections with 2-plane trees (which are in turn in bijection with 2-noncrossing increasing trees) are established. Among these structures are \(S\)-Motzkin paths ( introduced and enumerated by Prodinger and his coauthors in [14]), pairs of ternary trees (introduced by Knuth in his Annual Christmas Tree Lecture [15]) and some pattern avoiding sequences. It would be interesting to establish bijections between the set of these structures and the set of 2-noncrossing increasing trees.
The author wishes to thank the anonymous referees for the useful comments on the previous version of this paper.
Gu, N. S., Prodinger, H., & Wagner, S. (2010). Bijections for a class of labeled plane trees. European Journal of Combinatorics, 31(3), 720-732.
Gu, N. S., & Prodinger, H. (2009). Bijections for 2-plane trees and ternary trees. European Journal of Combinatorics, 30(4), 969-985.
Pang, S. X., & Lv, L. (2010, December). K-noncrossing trees and k-proper trees. In 2010 2nd International Conference on Information Engineering and Computer Science (pp. 1-3). IEEE.
Yan, S. H., & Liu, X. (2009). 2-noncrossing trees and 5-ary trees. Discrete Mathematics, 309(20), 6135-6138.
Okoth, I. O. (2021). Refined enumeration of \(2\)-noncrossing trees. Notes in Number Theory and Discrete Mathematics, 27(2), 201–210.
Asinowski, A., & Mansour, T. (2008). Dyck paths with coloured ascents. The Electronic Journal of Combinatorics29(5), 1262–1279.
Deutsch, E., & Noy, M. (2002). Statistics on non-crossing trees. Discrete Mathematics, 254(1-3), 75–87.
Flajolet, P., & Noy, M. (1999). Analytic combinatorics of non-crossing configurations. Discrete Mathematics, 204(1-3), 203–229.
Noy, M. (1998). Enumeration of noncrossing trees on a circle. Discrete Mathematics, 180(1-3), 301-313.
Okoth, I. O., & Wagner, S. (2015). Locally oriented noncrossing trees. The Electronic Journal of Combinatorics, 22(3). https://doi.org/10.37236/5164.
Stanley, R. P., & Fomin, S. (1999). Enumerative combinatorics. Vol. 2, volume 62 of. Cambridge studies in advanced mathematics, 25.
Comtet, L. (1974). Advanced Combinatorics: The art of finite and infinite expansions. Springer Science & Business Media.
Sloane, N. J. (2018). The on-line encyclopedia of integer sequences. Published electronically at https://oeis. org.
Prodinger, H., Selkirk, S. J., & Wagner, S. (2020). On two subclasses of Motzkin paths and their relation to ternary trees. Algorithmic Combinatorics: Enumerative Combinatorics, Special Functions and Computer Algebra: In Honour of Peter Paule on his 60th Birthday, 297-316.
Knuth, D. (2014). Donald Knuth’s 20th annual Christmas tree lecture:(3/2)-ary Trees. Lecture, Stanford University.