The eccentric atom-bond sum-connectivity \(\left(ABSC_{e}\right)\) index of a graph \(G\) is defined as \(ABSC_{e}(G)=\sum\limits_{uv\in E(G)}\sqrt{\frac{e_{u}+e_{v}-2}{e_{u}+e_{v}}}\), where \(e_{u}\) and \(e_{v}\) represent the eccentricities of \(u\) and \(v\) respectively. This work presents precise upper and lower bounds for the \(ABSC_{e}\) index of graphs based on their order, size, diameter, and radius. Moreover, we find the maximum and minimum \(ABSC_{e}\) index of trees based on the specified matching number and the number of pendent vertices.
Consider a simple and connected graph \(G\) with vertex set \(V(G)\) and edge set \(E(G)\). Let \(u\) and \(v\) be two vertices in \(V(G)\). The distance between vertices \(u\) and \(v\) in a graph \(G\) is represented by \(d_{G}(u, v)\) and is defined as the minimum number of edges that need to be traversed to reach from \(u\) to \(v\) via a shortest path. The degree of vertex \(v\) in graph \(G\) is denoted as \(d_{G}(v)\) and is defined as the number of vertices adjacent to \(v\). The set \(N_{G}(v)\), defined as \(\left\{u \in V(G) :d_{G}\left(u, v\right)=1\right\}\), represents the neighborhood set of vertex \(v\) in graph \(G\). A pendent vertex is a vertex with a degree of one. The eccentricity \(e_{v}\) of a vertex \(v\in V(G)\) is defined as the greatest distance between \(v\) and any other vertex \(u\). The diameter of a graph \(G\), denoted as \(d(G)\), is the highest number obtained by calculating the eccentricities of all its vertices and selecting the greatest one. The radius \(r(G)\) of graph \(G\) is defined as the minimum value among all the eccentricities of its vertices. A graph \(G\) is classified as a self-centred graph if each vertex \(v\) has the property that its eccentricity \(e_{v}\) is equal to the radius \(r(G)\) and the diameter \(d(G)\) of the graph. A tree \(T\) is a graph that exhibits the property of having a unique path connecting any pair of vertices. \(S_{n}\) symbol represents a star graph, whereas \(P_{n}\) represents a route graph. A pendent path \(P\) is a path with only one terminus connected to a vertex with a degree of one.
Topological indices play a vital role in mathematical chemistry. One can see the book [1]. Following the publication [2], numerous topological indices have been introduced. The Randić index is a well-researched topological index that was first defined in the paper [3]. Several academic papers and books have been written on the Randić index, two of which are referenced as [4,5]. Moreover, other topological indices have been suggested to enhance the prediction capacity of the Randić index. The first Zagreb index is commonly considered to be the main successor of the Randić index, which was examined in [6] and defined as follows: \[\label{Z1} Z(G):=\sum\limits_{uv\in E(G)}\left(d_{u}+d_{v}\right).\tag{1}\]
Sharma et al. [7] introduced the eccentric topological index. They defined the eccentric first Zegrab index as \[\label{Z2} Z_{e}(G):=\sum\limits_{uv\in E(G)}\left(e_{u}+e_{v}\right).\tag{2}\] Later on many authors attracted towards this topic, for example [8-10].
Estrada et al. [11] made alterations to the Randić index and introduced the atom-bond connectivity (\(ABC\)) index for graphs. This index was also examined in the articles [12,13]. The \(ABC\) index of graph G is formally defined as \[\label{def1} ABC(G):=\sum\limits_{uv\in E(G)}\sqrt{\frac{d_{u}+d_{v}-2}{d_{u}d_{v}}}.\tag{3}\] The author of the study [14] introduced the eccentric form of the atom-bond connectivity index. \[\label{def2} ABC_{e}(G):=\sum\limits_{uv\in E(G)}\sqrt{\frac{e_{u}+e_{v}-2}{e_{u}e_{v}}}.\tag{4}\] Ali et al. [15,16] altered the \(ABC\) index and proposed the atom-bond sum connectivity (\(ABSC\)) index for graphs. The \(ABSC\) index of a graph \(G\) is precisely defined as \[\label{D1} ABSC(G):=\sum\limits_{uv\in E(G)}\sqrt{\frac{d_{u}+d_{v}-2}{d_{u}+d_{v}}}=\sum\limits_{uv\in E(G)}\sqrt{1-\frac{2}{d_{u}+d_{v}}}.\tag{5}\] This study’s primary aim is to precisely define the eccentric atom-bond sum-connectivity \((ABSC_{e})\) index for graphs. The \(ABSC_{e}\) index is determined by substituting the degrees of the vertices with their eccentricities, which may be stated mathematically as \[\label{D2} ABSC_{e}\left(G\right)=\sum\limits_{uv\in E(G)}\sqrt{\frac{e_{u}+e_{v}-2}{e_{u}+e_{v}}}=\sum\limits_{uv\in E(G)}\sqrt{1-\frac{2}{e_{u}+e_{v}}}.\tag{6}\]
The field of chemical graph theory is appealing to scholars because of its numerous applications, wide range of topics, and its ability to provide a direct understanding of everyday events for instant one can see [17-23].
Lemma 1 ([24]). Let \(I(u, v)=\sqrt{1-\frac{2}{u+v}}\) be a function, where \(\min\left\{u, v\right\}\geq 1\). Then \(I(u,v)\) is strictly increasing in \(u\) and \(v\).
The following are the basic tasks of this research:
Determine tight upper and lower bounds for the \(ABSC_{e}\) index of graphs using different parameters such as order, size, diameter, and radius; also recognize and explain the graphs that meet these bounds.
Determine the maximum and minimum values of the \(ABSC_{e}\) index for trees based on the matching number; also identify the trees that reach extreme values.
Determine the maximum and minimum values of the \(ABSC_{e}\) index for trees based on the provided number of pendent vertices; also identify the trees that reach extreme values.
It is obvious that \(ABSC_{e}\left(K_{n}\right)=0\). Thus the complete graph yields the lowest possible value for the \(ABSC_{e}\) index. Therefore, in this section, we will only discuss that case when the graph under consideration is not \(K_n\).
Theorem 2. Let \(G\) be an \(m\) edged, simple, connected graph having \(r=r(G)\geq 2\) radius and \(d=d(G)\) diameter. Then \[m\sqrt{1-\frac{1}{r}}\leq ABSC_{e}\left(G\right)\leq m\sqrt{1-\frac{1}{d}},\] The equality is true if and only if \(G\) is a self-centred graph.
Proof. We know that \[\sqrt{\frac{e_{u}+e_{v}-2}{e_{u}+e_{v}}}=\sqrt{1-\frac{2}{e_{u}+e_{v}}}.\]
Lemma 1 establishes that this function exhibits a monotonically increasing behavior. Therefore, \[\sqrt{1-\frac{1}{r}}\leq\sqrt{1-\frac{2}{e_{u}+e_{v}}}\leq \sqrt{1-\frac{1}{d}}.\] Upon performing the summing, we obtain the desired result. Moreover, note that the equality true if and only if eccentricity of each vertex is same which happens only when graph is self-centred. ◻
Lemma 3 ([25]). Consider a positive \(m\)-tuple \(\left(p_{1}, p_{2}, \ldots, p_{m}\right)\), where there exist positive numbers \(p\) and \(q\) such that \(0 <p\leq p_{i}\leq q\). Subsequently \[\frac{m\sum\limits_{i=1}^{m}p_{i}^{2}}{\left(\sum\limits_{i=1}^{m}p_{i}\right)^{2}}\leq \frac{1}{4}\left(\sqrt{\frac{q}{p}}+\sqrt{\frac{p}{q}}\right)^{2},\] the equality is true if and only if \(p=q\) or \[r=\left(\frac{q}{q+p}\right)m,\] is an integer representing the number of \(p_{i}\) numbers that are equal to \(p\), and let \(m-r\) be the number of \(p_{i}\) numbers that are equal to \(q\) (where \(q\) is not equal to \(p\)).
The eccentric harmonic \(H_{e}(G)\) index of a graph \(G\) is defined as stated in the paper [10]. \[H_{e}\left(G\right):=\sum\limits_{uv\in E(G)}\frac{2}{e_{u}+e_{v}}.\tag{7}\]
Theorem 4. Let \(G\) be an \(m\) edged, simple, connected graph having \(r=r(G)\geq 2\) radius and \(d=d(G)\) diameter. Then \[\frac{2\sqrt{\left(m-H_{e}\left(G\right)\right)m\sqrt{rd\left(r-1\right)\left(d-1\right)}}}{\sqrt{d\left(r-1\right)}+\sqrt{r\left(d-1\right)}}\leq ABSC_{e}(G).\]
Proof. It follows from Theorem 1 that \[\sqrt{1-\frac{1}{r}}\leq\sqrt{1-\frac{2}{e_{u}+e_{v}}}\leq \sqrt{1-\frac{1}{d}}.\] Consider \(\sqrt{1-\frac{1}{r}}=p\) and \(\sqrt{1-\frac{1}{d}}=q\), then it follows from Lemma 1, we have \[\left(\sum\limits_{uv\in E(G)}\sqrt{1-\frac{2}{e_{u}+e_{v}}}\right)^{2}\geq \sum\limits_{uv\in E(G)}\left(1-\frac{2}{e_{u}+e_{v}}\right) \times \frac{4m\sqrt{rd\left(r-1\right)\left(d-1\right)}}{\left(\sqrt{d\left(r-1\right)}+\sqrt{r\left(d-1\right)}\right)^{2}} .\] After some easy calculations, we get \[\left(\sum\limits_{uv\in E(G)}\sqrt{1-\frac{2}{e_{u}+e_{v}}}\right)^{2}=\frac{\left(m-H_{e}(G)\right)4m\sqrt{rd\left(r-1\right)\left(d-1\right)}}{\left(\sqrt{d\left(r-1\right)}+\sqrt{r\left(d-1\right)}\right)^{2}}.\\ \] Therefore, \[ABSC_{e}(G)\geq \frac{2\sqrt{\left(m-H_{e}\left(G\right)\right)m\sqrt{rd\left(r-1\right)\left(d-1\right)}}}{\sqrt{d\left(r-1\right)}+\sqrt{r\left(d-1\right)}}.\] ◻
Theorem 5. Let \(G\) be an \(m\) edged, simple, connected graph having \(r=r(G)\geq 2\) radius and \(d=d(G)\) diameter. Then \[m\sqrt{\frac{r-1}{d}}\leq ABSC_{e}\left(G\right)\leq m\sqrt{\frac{d-1}{r}},\] the equality is true if and only if \(G\) is a self-centered graph.
Proof. For \(uv\in E(G)\), we have \[\sqrt{\frac{e_{u}+e_{v}-2}{e_{u}+e_{v}}}=\sqrt{\frac{1}{e_{u}+e_{v}}}.\sqrt{e_{u}+e_{v}-2}.\]
It can be deduced from \[\sqrt{2\left(r-1\right)}\leq \sqrt{e_{u}+e_{v}-2}\leq \sqrt{2\left(d-1\right)}\] and \[\sqrt{\frac{1}{2d}}\leq \sqrt{\frac{1}{e_{u}+e_{v}}}\leq \sqrt{\frac{1}{2r}}\] that \[m\sqrt{\frac{r-1}{d}}\leq ABSC_{e}\left(G\right)\leq m\sqrt{\frac{d-1}{r}}.\] The equation \(r=d\) holds exclusively when \(G\) is a self-centred graph and conversely. Thus, the equality is valid only when \(G\) is a self-centred graph. ◻
Lemma 6 ([26]). Let \(q_{i}\) and \(r_{i}\) be the real numbers, where \(1\leq i\leq m\) such that \(Qq_{i}\leq r_{i}\leq Rq_{i}\) for each \(1\leq i\leq m\), with \(0<Q\leq R\). Then \[\left(Q+R\right)\sum\limits_{i=1}^{m}q_{i}r_{i}\geq \sum\limits_{i=1}^{m}r_{i}^{2}+QR\sum\limits_{i=1}^{m}q_{i}^{2},\] the equality is true if and only if either \(r_{i}=Qq_{i}\) or \(r_{i}=Rq_{i}\) for each \(1\leq i\leq m\).
Theorem 7. Let \(G\) be an \(m\) edged, simple, connected graph having \(r=r(G)\geq 2\) radius and \(d=d(G)\) diameter. Then \[\label{e22} ABSC_{e}(G)\geq \frac{Z_{e}(G)+2\left(-m+H_{e}(G)\sqrt{dr(d-1)(r-1)}\right)} {2\left(\sqrt{d(d-1)}+\sqrt{r(d-1)}\right)},\tag{8}\] the equality is true if and only if \(G\) is a self-centered graph.
Proof. We know that \[\begin{aligned} \sqrt{2(r-1)}\leq\sqrt{e_{u}+e_{v}-2}\leq\sqrt{2(d-1)}, \end{aligned}\] \[\sqrt{ \frac{1}{e_{u}+e_{v}}}\sqrt{2r}\sqrt{2(r-1)}\leq \sqrt{e_{u}+e_{v}-2}\leq \sqrt{ \frac{1}{e_{u}+e_{v}}}\sqrt{2d}\sqrt{2(d-1)},\] and \[\sqrt{\frac{1}{e_{u}+e_{v}}}2\sqrt{r(r-1)}\leq\sqrt{e_{u}+e_{v}-2}\leq\sqrt{\frac{1}{e_{u}+e_{v}}}2\sqrt{d(d-1)}.\] From the definition of \(ABSC_{e}\), we have \[\begin{aligned} ABSC_{e}(G) = & \sum\limits_{uv\in E(G)}\sqrt{\frac{1}{e_{u}+e_{v}}}\cdot\sqrt{e_{u}+e_{v}-2} \\ = & \frac{\left[2\sqrt{r(r-1)}+2\sqrt{d(d-1)}\right]} {2\sqrt{r(r-1)}+2\sqrt{d(d-1)}}\sum\limits_{uv\in E(G)}\left(\sqrt{\frac{1}{e_{u}+e_{v}}}\cdot\sqrt{e_{u}+e_{v}-2}\right). \end{aligned}\] Consider \(\sqrt{\frac{1}{e_{u}+e_{v}}}=q_{i}\), \(2\sqrt{r(r-1)}=Q\), \(2\sqrt{d(d-1)}=R\) and \(\sqrt{e_{u}+e_{v}-2}=r_{i}\), then it follows from Lemma 6, we have \[\begin{aligned} ABSC_{e}(G)\geq& \frac{\left[\left(\sum\limits_{uv\in E(G)}\frac{1}{e_{u}+e_{v}}\right)\left(2\sqrt{r(r-1)}\times2\sqrt{d(d-1)}\right) +\sum\limits_{uv\in E(G)}\left(e_{u}+e_{v}-2\right)\right]}{2\sqrt{r(r-1)}+2\sqrt{d(d-1)}}\\ = & \frac{Z_{e}(G)+2\left(-m+H_{e}(G)\sqrt{dr(d-1)(r-1)}\right)} {2\left(\sqrt{d(d-1)}+\sqrt{r(d-1)}\right)}, \end{aligned}\] the equality condition states that each edge must either satisfy \(e_{u}=e_{v}=r\) or \(e_{u}=e_{v}=d\). This suggests that the graph is self-centred. In contrast, it is clear that in the case of a self-centred graph, the equality holds in (8). ◻
A matching \(M\) is a subset of the edge set in which no two edges share a vertex. The matching number of the graph is defined as the size of the largest possible matching in \(G\). An \(m\)-matching graph \(G\) is a subset \(M\) of edges in \(G\) that contains exactly \(m\) edges. A vertex \(v\) in graph \(G\) is considered \(M\)-saturated if connected to an edge in \(M\). If every vertex of graph \(G\) is matched by the matching \(M\), then \(M\) is a perfect matching.
Let \(2\leq 2m\leq n\), and \(x, y\geq 1\) be positive integers. Consider a set of trees of order \(n\) with matching number \(m\) denoted as \(\mathcal{T}_{n,m}\). Suppose \(\mathcal{T}_{n,m}^{*}\) be the subset of \(\mathcal{T}_{n,m}\) consisting of trees that satisfy the condition \(n>2m\). These trees are formed by linking two stars, denoted as \(S_{x}\) and \(S_{y}\), with a path of length \(2\left(m-1\right)\) between their central vertices. The values of \(x\) and \(y\) are determined by the equation \(x+y=n-\left(2m-3\right)\) as shown in Figure 1.
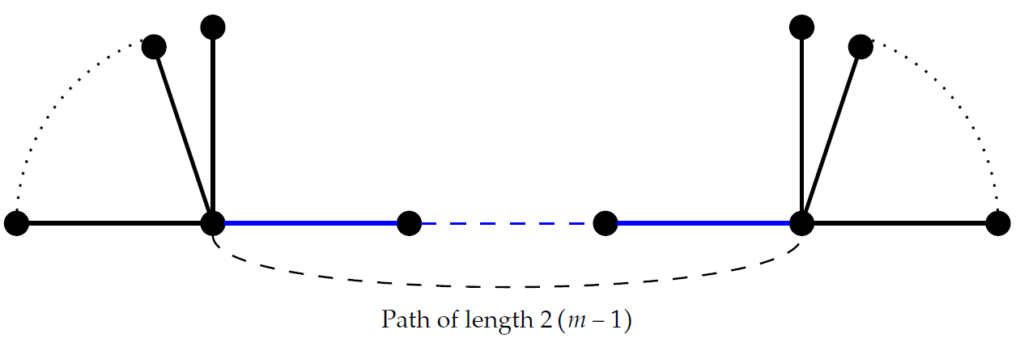
It should also be noted that all the trees in \(\mathcal{T}_{n,m}^{*}\) have the same \(ABSC_{e}\) index. In this paper we denote the \(ABSC_{e}\) index of any tree from \(\mathcal{T}_{n,m}^{*}\) with the notation \(g\left(n, m\right)\).
The tree \(S_{n,m}\) is defined as a tree of order \(n\) that is derived from a star \(S_{n-m+1}\) by adding a pendent edge to each of a specific \(m-1\) non-central vertices of \(S_{n-m+1}\). It is evident that \(S_{n,m}\) belongs to the set \(\mathcal{T}_{n,m}\). Let \(f\left(n, m\right)\) be the \(ABSC_{e}\) index of \(S_{n,m}\). An example of \(S_{n, m}\) shown in Figure 2.
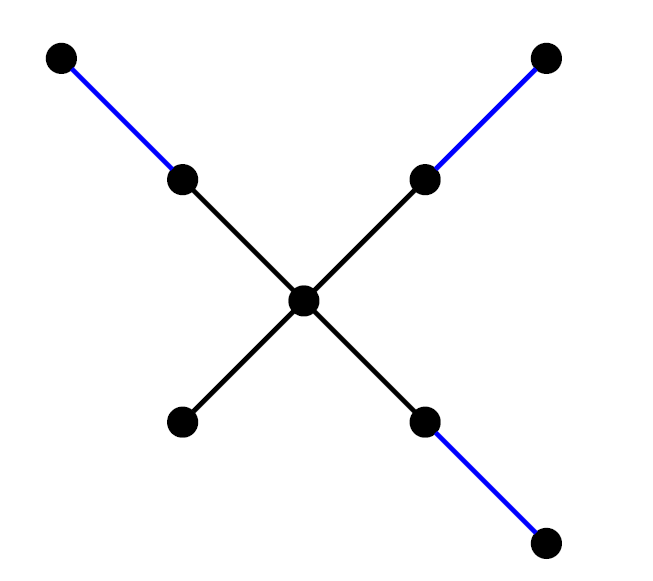
Let \(uv\) be an edge of \(G\). Let \(G^{*}\) be the graph obtained from \(G\) by contracting the edge \(uv\) into a new vertex \(u^{*}\) and adding a new pendent edge \(u^{*}v^{*}\) where \(v^{*}\) is a new pendent vertex. We say that \(G^{*}\) is obtained from \(G\) by separating an edge \(uv\) as shown in Figure 3.
Lemma 8 ([27]). Consider a tree \(T\) with an order of \(n\geq 3\) and a perfect matching. Then, \(T\) must possess a minimum of two pendent vertices, each connected to a vertex with a degree of 2.
Lemma 9 ([27]). Consider a tree \(T\) with \(n\) vertices and a \(m\)-matching, where \(n\) is more than \(2m\). There exists a \(m\)-matching \(M\) and a pendent vertex \(v\) such that \(v\) is a vertex in \(M\) that is not next to any other vertex in \(M\).
Lemma 10. Consider a connected graph \(G\) with a cut edge \(e=uv\). Let \(G-uv\) be the graph obtained by removing the edge \(uv\) from \(G\). Suppose that \(G-uv\) can be partitioned into two components \(G_1\) and \(G_2\), where \(|V(G_1)|, |V(G_2)| \geq 2\). Furthermore, \(G_1\) contains the vertex \(u\) and \(G_2\) contains the vertex \(v\). Let \(G^{*}\) be the graph formed from \(G\) by isolating the edge \(uv\). Then \(ABSC_{e}(G)>ABSC_{e}(G^{*})\).
Proof. Consider the graph \(G^{*}\), which is derived from \(G\) by contracting the edge \(uv\) into a single vertex \(u^{*}v^{*}\). In \(G^{*}\), \(v^{*}\) is a pendant vertex, as illustrated in Figure 3. Note that \(\left|E(G)\right|=\left|E(G^{*})\right|\) and \(\left|V(G)\right|=\left|V(G^{*})\right|\) and also \(e_{G}(u)+e_{G}(v)=e_{G^{*}}(u^{*})+e_{G^{*}}(v^{*})\), \(e_{G^{*}}(i)\leq e_{G}(i)\) for all \(i\in V(G^{*})\backslash \left\{u^{*}, v^{*}\right\}\) and \(e_{G^{*}}(u^{*})\leq \min\left\{e_{G}(u), e_{G}(v)\right\}\). Thus we have \[\begin{aligned} & ABSC_{e}(G^{*})-ABSC_{e}(G)\\ = &\sum\limits_{\substack{ij\in E(G^{*})\\ i, j\in V(G)\backslash\left\{u, v\right\}}}\left(\sqrt{1-\frac{2}{e_{G^{*}}(i)+e_{G^{*}}(j)}}-\sqrt{1-\frac{2}{e_{G}(i)+e_{G}(j)}}\right)\\ &+\left(\sqrt{1-\frac{2}{e_{G^{*}}(u^{*})+e_{G^{*}}(v^{*})}}-\sqrt{1-\frac{2}{e_{G}(u)+e_{G}(v)}}\right)\\ &+\sum\limits_{\substack{u^{*}i\in E(G^{*})\\ i\in V(G)\backslash\left\{u, v\right\}}}\sqrt{1-\frac{2}{e_{G^{*}}(u^{*})+e_{G^{*}}(i)}}-\sum\limits_{\substack{ij\in E(G), j\in \left\{u, v\right\}\\ i\in V(G)\backslash\left\{u, v\right\}}}\sqrt{1-\frac{2}{e_{G}(j)+e_{G}(i)}}, \end{aligned}\] by using Lemma 1, it may be inferred that \(ABSC_{e}(G^{*})-ABSC_{e}(G)<0\), which completes our arguments. ◻
Theorem 11. Let \(T\in \mathcal{T}_{n,m}\) be a tree. If \(n=2m\), then \[\label{E2.1} ABSC_{e}(T)\leq ABSC_{e}(P_{2m}),\] and if \(n>2m\), then \[\label{E2.2} ABSC_{e}(T)\leq g\left(n, m\right),\] the equality is true if and only if \(T\in \mathcal{T}_{n,m}^{*}\).
Proof. Let \(u\) and \(v\) be two vertices in \(T\). If both \(u\) and \(v\) have the same eccentricity, denoted as \(e_{u}\) and \(e_{v}\) respectively, and this eccentricity is equal to the diameter of \(T\), denoted as \(d(T)\), then \(e_{u}=e_{v}=d(T)\) then both \(u\) and \(v\) are pendant vertices. If the tree \(T\) has a pendant vertex \(w\) distinct from \(u\) and \(v\). Transfer the adjacent edge containing the element \(w\) to the vertex \(u\). The new tree is represented as \(T^{'}\). It is important to observe that \(\left|E(T)\right|=\left|E(T^{'})\right|\) and \(V(T)=V(T^{'})\) and also \(e_{T}(w)\leq e_{T^{'}}(w)\) for all \(w\in V(T)\). By the definition of \(ABSC_{e}\) index, we have \(ABSC_{e}(T)\leq ABSC_{e}(T^{'})\). Repeat this procedure up to \(2m-d(T)\) times until the resulting graph \(\widetilde{T}\) contains the longest path in \(\mathcal{T}_{n,m}\). So \(ABSC_{e}(T)\leq ABSC_{e}(\widetilde{T})\). If \(n=2m\), then \(\widetilde{T}=P_{2m}\). On the other hand if \(n>2m\), then suppose that \(P=v_{1}v_{2}\cdots v_{2m+1}\) is the longest path in \(\widetilde{T}\). It is evident that the set \(V\left(\widetilde{T}\right)\backslash \left\{v_{1}, v_{2}, \ldots, v_{2m+1}\right\}\) contains only pendent vertices. Alternatively, a pendent path with a minimum length of 2 exists. We can get an \(\left(m+1\right)\)-matching obtained by taking a pendent edge in such pendent path and \(m\) mutually independent edges in \(P\), which is a contradiction.
Similarly, transfer pendent edge except \(v_{2m}v_{2m+1}\) and \(v_{1}v_{2}\) to the vertices \(v_{2}\) or \(v_{2m}\) at a time. At most \(n-\left(2m+1\right)\) times, repeat this process until the resulting tree is \(T^{*}\in \mathcal{T}_{n,m}^{*}\). Therefore, \(ABSC_{e}(T) \leq ABSC_{e}(T^{*})\). ◻
Theorem 12. Let \(T\in \mathcal{T}_{2m, m}\). Then \[ABSC_{e}(T)\geq f\left(2m, m\right),\] the equality is true if and only if \(T\cong S_{2m, m}\).
Proof. We will demonstrate this, by using induction on \(m\). If \(1\leq m\leq3\), then the proof is obvious. Consider \(m\geq 4\). Let \(M\) be a perfect matching in \(T\). Consider \(uv\) from \(M\) is a non-pendent edge then \(T^{0}\) can be formed from \(T\) by separating \(uv\), then \(T^{0}\) contains a perfect matching \(M_{1}=M\cup \left\{u^{*}v^{*}\right\}\backslash \left\{uv\right\}\). Continue doing this until the most recent perfect matching has no non-pendent edges. Let \(\widetilde{T}\) be the resulting tree and \(\widetilde{M}\) be the associated perfect matching. If at least one separation is performed, then according to Lemma 10, we obtain, \(ABSC_{e}(T)>ABSC_{e}(\widetilde{T})\). It may be inferred that every edge in \(\widetilde{T}\) is a pendent edge. According to Lemma 8, \(\widetilde{T}\) has a pendent vertex \(u\) that is connected to a vertex \(v\) of degree 2. Suppose \(N(v)=\left\{u, x\right\}\), and assuming \(T^{*}=\widetilde{T}-u-v\), we may conclude that \(T^{*}\in \mathcal{T}_{2(m-1), m-1}\). Suppose that the degree of \(x\) is \(d\) and \(N(x)\backslash \left\{v\right\}=\left\{u_{1}, u_{2}, \ldots, u_{d-1}\right\}\). Recall that \(\widetilde{M}\) is a perfect matching that exclusively consists of pendent edges, so the degree of \(x\) must be greater than 2 in order to avoid the presence of a non-pendent edge in \(\widetilde{M}\) that includes an endpoint \(x\), which leads a contradiction. For simplicity, suppose that \(xu_{1}\in \widetilde{T}\), which means that the degree of \(u_{1}\) is one. Additionally, we have \(d(u_{i})\geq 2\) for \(2\leq i\leq d-1\), also note that \(e_{\widetilde{T}}(j)\geq e_{T^{*}}(j)\) for all \(j\in V(T^{*})\). From the definition of \(ABSC_{e}\) we have \[\begin{aligned} & ABSC_{e}(\widetilde{T})-ABSC_{e}(T^{*})\\ = &\sum\limits_{\substack{x_{1}x_{2}\in E(T^{*})\\ x_{1}, x_{2}\in V(T^{*})}}\left(\sqrt{1-\frac{2}{e_{\widetilde{T}}(x_{1})+e_{\widetilde{T}}(x_{2})}}-\sqrt{1-\frac{2}{e_{T^{*}}(x_{1})+e_{T^{*}}(x_{2})}}\right)\\ &+\sqrt{1-\frac{2}{e_{\widetilde{T}}(x)+e_{\widetilde{T}}(v)}}+\sqrt{1-\frac{2}{e_{\widetilde{T}}(u)+e_{\widetilde{T}}(v)}}. \end{aligned}\] Using Lemma 1, we get \[\sqrt{1-\frac{2}{e_{\widetilde{T}}(x_{1})+e_{\widetilde{T}}(x_{2})}}\geq\sqrt{1-\frac{2}{e_{T^{*}}(x_{1})+e_{T^{*}}(x_{2})}},\] so we have \[\begin{aligned} ABSC_{e}(\widetilde{T})-ABSC_{e}(T^{*})\geq&\sqrt{1-\frac{2}{e_{\widetilde{T}}(x)+e_{\widetilde{T}}(v)}}+\sqrt{1-\frac{2}{e_{\widetilde{T}}(u)+e_{\widetilde{T}}(v)}}\\ \geq&\sqrt{1-\frac{2}{4r\left(\widetilde{T}\right)-1}}+\sqrt{1-\frac{2}{4r\left(\widetilde{T}\right)-3}}. \end{aligned}\] Recall that \(m\geq 4\). By Lemma 8, \(r\left(\widetilde{T}\right)\geq 2\). Then \[ABSC_{e}(\widetilde{T})-ABSC_{e}(T^{*})\geq \sqrt{1-\frac{2}{7}}+\sqrt{1-\frac{2}{5}},\] the equality is true if and only if \(r\left(\widetilde{T}\right)=2\). By our assumption, we have \[\begin{aligned} ABSC_{e}(\widetilde{T})\geq& ABSC_{e}(T^{*})+\sqrt{1-\frac{2}{7}}+\sqrt{1-\frac{2}{5}}\\ \geq& f\left(2\left(m-1\right), m-1\right)+\sqrt{1-\frac{2}{7}}+\sqrt{1-\frac{2}{5}}\\ = &f\left(2m, m\right), \end{aligned}\] the equality is true if and only if \(T \cong S_{2m, m}\). ◻
Let \(T\in \mathcal{T}_{n, 2}\), and \(n\geq 4\). Then it is easy to verify that \(ABSC_{e}(T)\geq f\left(n, 2n\right)\), with the equality if and only if \(T\in \mathcal{T}_{n, 2}^{*}\) and \(d(T)=3\). It is evident that \(S_{n, 2}\) is the only graph in \(\mathcal{T}_{n, 2}\) that has the mainimum \(ABSC_{e}\) index.
Theorem 13. Let \(T\in \mathcal{T}_{n, m}\), and \(6\leq 2m\leq n\). Then \[ABSC_{e}(T)\geq f\left(n, m\right),\] the equality is true if and only if \(T\cong S_{n, m}\).
Proof. We will demonstrate this, by using induction on \(n\). If \(n=2m\), then the result may be deduced from Theorem 12. Suppose that \(n>2m\) and it holds for all trees in \(\mathcal{T}_{n-1, m}\). Lemma 9 states that \(T\) possesses an \(m\)-matching \(M\) and a pendent vertex \(v\) that is not saturated by \(M\). Let \(u\in V(T)\) such that \(N(u)=\left\{v, v_{1}, v_{2}, \ldots, v_{d-1} \right\}\) and degree of \(u\) is \(d\). Suppose that \(T^{*}=T-v\), additionally, it should be noted that \(e_{T}(j)\geq e_{T^{*}}(j)\) for every vertex \(j\) in \(V(T^{*})\). Therefore, we have \[\begin{aligned} ABSC_{e}(T)-ABSC_{e}(T^{*})= &\sum\limits_{\substack{x_{1}x_{2}\in E(T^{*})\\ x_{1}, x_{2}\in V(T^{*})}}\left(\sqrt{1-\frac{2}{e_{T}(x_{1})+e_{T}(x_{2})}}\right.\\ &-\left.\sqrt{1-\frac{2}{e_{T^{*}}(x_{1})+e_{T^{*}}(x_{2})}}\right)\\ &+\sqrt{1-\frac{2}{e_{T}(u)+e_{T}(v)}}. \end{aligned}\] From Lemma 1, we get \[\sqrt{1-\frac{2}{e_{T}(x_{1})+e_{T}(x_{2})}}\geq\sqrt{1-\frac{2}{e_{T^{*}}(x_{1})+e_{T^{*}}(x_{2})}},\] so, we get \[ABSC_{e}(T)-ABSC_{e}(T^{*})\geq \sqrt{1-\frac{2}{e_{T}(u)+e_{T}(v)}}\geq \sqrt{1-\frac{2}{2r(T)+1}}.\] Remember that \(m\geq 3\) and \(r\left(T\right)\geq 2\). Thus we have \[\begin{aligned} ABSC_{e}(T)\geq ABSC_{e}(T^{*})+\sqrt{1-\frac{2}{5}}\geq f\left(n-1, m\right)+\sqrt{1-\frac{2}{5}}=f\left(n, m\right), \end{aligned}\] the equality is true if and only if \(T\cong S_{n, m}\). We have concluded our arguments. ◻
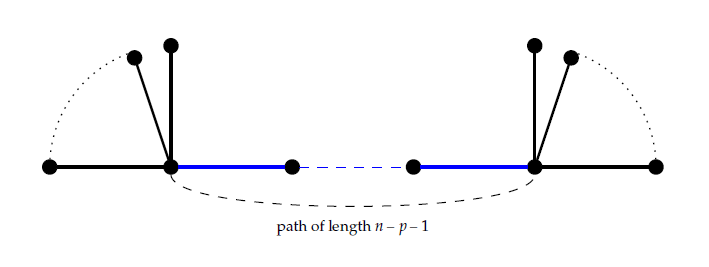
Consider positive integers \(n\) and \(p\) such that \(n\) and \(p\) are greater than or equal to 2. Let \(x\) and \(y\) be positive integers greater than or equal to 1. Let’s examine a group of trees, represented as \(\mathcal{T}_{n,p}\), where each tree has a total of \(n\) vertices and \(p\) of them are pendent. Define \(\mathcal{T}_{n,p}^{*}\) as the collection of trees with an order of \(n\). These trees are formed by connecting the path of length \(n-p-1\) between the central vertices of two stars, denoted as \(S_{x}\) and \(S_{y}\). The condition for the values of \(x\) and \(y\) is that their sum equals \(p+2\). The Structure of \(\mathcal{T}_{n,p}^{*}\) graphs is depicted in Figure 4.
The tree \(S_{n, p}\) is a tree with \(n\) vertices formed by connecting \(p\) pendent paths to a central vertex, with each path having a variation in length of at most one, as shown in Figure 5.
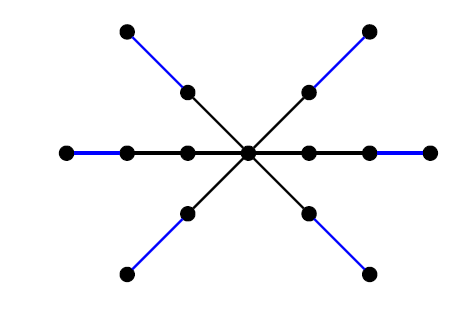
It is clear that, \(\mathcal{T}_{n,p}^{*}\subset \mathcal{T}_{n,p}\) and \(S_{n,p}\in \mathcal{T}_{n,p}\). It is important to observe that all the trees in \(\mathcal{T}_{n,p}^{*}\) have the same \(ABSC_{e}\) index, which is represented by \(q\left(n ,p\right)\). Let \(h\left(n, p\right)\) be the \(ABSC_{e}\) index of \(S_{n, p}\).
Consider a pendent path \(P=u_{1}u_{2}\cdots u_{r}\), and let \(v\notin V(P)\). Consider the graph \(G^{*}\), which is obtained from \(G\) by replacing the pendent path \(P\) with a single edge from vertex \(u_{2}\) to vertex \(v\) such that \(G^{*}=G-u_{1}u_{2}+u_{2}v\). We say \(G^{*}\) is derived from \(G\) by relocating the pendent path \(P\) to the vertex \(v\).
Lemma 14 ([28]). Let \(T\in \mathcal{T}_{n,p}\). Then the diameter of tree \(d(T)\leq n-p+1\).
Theorem 15. Let \(T\) be a tree with \(n\) vertices and \(m\) edges. Then \[ABSC_{e}(T)\geq m\sqrt{\frac{1}{3}},\] the equality is true if and only if \(T\cong S_{n}\).
Proof. Suppose \(T\) is a
tree of \(n\) vertices and \(m\) edges. Next, we consider two
cases:
Case 1. There is a vertex \(v\) such that its degree is \(n-1\). This shows that \(T\) is a star graph and \(e_{v}=1\) and \(e_{u}=2\) for every \(u\in V(T)\backslash \left\{v\right\}\).
Then \[\begin{aligned}
ABSC_{e}(T)=\sum\limits_{uv\in
E(G)}\sqrt{1-\frac{2}{e_{u}+e_{v}}}=m\sqrt{\frac{1}{3}}.
\end{aligned}\] Case 2. There is no
vertex in the graph having degree \(n-1\). Then for all edges \(e_{v}\geq 2\) for \(1\leq v\leq n\), so \(e_{v}+e_{u}\geq 4\) for all edges in \(E(T)\). Then \[ABSC_{e}(T)=\sum\limits_{uv\in
E(G)}\sqrt{1-\frac{2}{e_{u}+e_{v}}}\geq
m\sqrt{\frac{1}{2}}>m\sqrt{\frac{1}{3}}.\] ◻
Theorem 16. Let \(2\leq p\leq n-2\) and \(T\in \mathcal{T}_{n,p}\). Then \[ABSC_{e}(T)\geq h\left(n, p\right),\] the equality is true if and only if \(T\cong S_{n,p}\).
Proof. Suppose \(P=u_{1}u_{2}\cdots u_{d(T)}u_{d(T)+1}\) is
a longest path in \(T\). Obviously
\(u_{1}\) and \(u_{d(T)+1}\) are two pendent vertices in
\(T\). Select a vertex \(v_{0}\in \left\{v : \min e_{p}(v), v\in
V(P)\right\}\). This vertex \(v_{0}\) should be the central vertex of
\(P\). If there is a pendent path in
\(T\) whose both ends do not contain
\(v_0\), then move the pendent path to
\(v_{0}\). Let \(\widetilde{T}\) represents this new tree.
It should be noted that \(\widetilde{T}\in
\mathcal{T}_{n,p}\). Moreover, \(T\) and \(\widetilde{T}\) possess identical order and
size, and additionally, \(e_{T}(v)\geq
e_{\widetilde{T}}(v)\) for any vertex \(v\in V(T)\). Therefore, we have \(ABSC_{e}\left(T\right)\geq
ABSC_{e}\left(\widetilde{T}\right)\). Repeat this process up to
maximum of \(p-2\) times until all
pendent paths include a non-pendent end point \(v_{0}\). The final resulting tree \(T^{*}\) is a member of the set \(\mathcal{T}_{n,p}\) and satisfies \(ABSC_{e}\left(T\right)\geq
ABSC_{e}\left(T^{*}\right)\). Furthermore, \(T^{*}\) is a tree consisting of one vertex
\(v_{0}\) with a degree of \(p\) and \(n-1\) vertices with degrees that are less
than or equal to 2. In order to establish the validity of our result, it
is sufficient to prove the following claim.
Claim 1. Let \(T^{*}\in \mathcal{T}_{n,p}\) be a tree that
contains precisely one vertex of degree \(p\). Then \[ABSC_{e}\left(T^{*}\right)\geq h\left(n
,p\right),\] the equality is true if and only if \(T=S_{n,p}\).
Proof. Select longest and shortest pendent paths in \(T^{*}\), then move the pendent edge from the longest pendent path to the pendent vertex of the shortest pendent path. Represent this newly formed tree as \(T^{'}\). It should be noted that \(T^{'}\in \mathcal{T}_{n,p}\) and has the same size and order. Furthermore, for each vertex \(j\) in \(V(T^{*})\), \(e_{T^{*}}(j)\geq e_{T^{'}}(j)\). Therefore \(ABSC_{e}(T^{*})\geq ABSC_{e}(T^{'})\). Repeat this process maximum of \(n-p\) times until all pendent paths have length \(l\) or \(l+1\), where \(l=[\frac{n-1}{p}]\). It should be noted that the graph obtained at the end is \(S_{n,p}\) and \(ABSC_{e}\left(T^{*}\right)\geq ABSC_{e}\left(S_{n,p}\right)=h\left(n, p\right)\). This concludes our arguments. ◻
Theorem 17. Let \(T\in \mathcal{T}_{n,p}\), for \(2\leq p\leq n-1\) and \(n\geq 5\). Then \[ABSC_{e}\left(T\right)\leq q\left(n, p\right),\] the equality is true if and only if \(T\in \mathcal{T^{*}}_{n,p}\).
Proof. It is straightforward for \(p=2\). Assume that \(p\geq 3\). We will demonstrate this, by
using induction on \(n\). For \(n=4\), \(T\in
\mathcal{T^{*}}_{4,3}\). The result follows. Suppose that \(n\geq5\) and \(ABSC_{e}\left(T\right)\leq q\left(n,
p\right)\) is true for all the trees with \(n-1\) vertices. Consider a tree \(T\) that has the minimum \(ABSC_{e}\) index among all the trees in
\(\mathcal{T}_{n,p}\). Consider \(P(T)\) as the set of all pendent vertices
of \(T\). Consider a vertex \(u\) that is adjacent to the pendent vertex
\(v\) in the tree \(T\). In order to proceed, it is necessary
to first establish the validity of the following claim.
Claim 1. There exists vertex \(v\) in the \(P(T)\) such that \(ABSC_{e}(T)=ABSC_{e}(T-v)+\sqrt{1-\frac{2}{e(v)+e(u)}}\).
Proof. Consider a set \(N^{'}(T)=\left\{v : e(v)=d(T), v\in P(T)
\right\}\). If \(P(T)-N^{'}(T)=\emptyset\), since \(p\geq 3\), then there exists at least one
vertex \(v\) in \(P(T)\) such that \(d\left(T-v\right)=d(T)\). If \(P(T)-N^{'}(T)\neq \emptyset\), then
take \(v\in P(T)-N^{'}(T)\). From
the above both cases, we have \(e_{T}(j)=e_{T-v}(j)\) for any vertex \(j\in V\left(T-v\right)\). Therefore our
claim is true.
Continue to prove Theorem 17. Let us assume that the pendent vertex \(v\) in \(T\) meets Claim 1. Now we will examine
further two cases:
Case 1. \(d(u)=2\). \(T-v\) has \(p\) pendant vertices. Using the assumption
made in the induction, the statements of Lemma 14 and Claim 1, we have
\[\begin{aligned}
ABSC_{e}\left(T\right)= &
ABSC_{e}\left(T-v\right)+\sqrt{1-\frac{2}{e_{T}(v)+e_{T}(u)}}\\
\leq&
ABSC_{e}\left(T-v\right)+\sqrt{1-\frac{2}{2d(T)-1}}\\
\leq& q\left(n-1, p\right)+
\sqrt{1-\frac{2}{2n-2p+1}}<q\left(n, p\right).
\end{aligned}\] The last inequality is valid because \(q\left(n, p\right)-q\left(n-1,
p\right)>\sqrt{1-\frac{2}{2n-2p+1}}\).
Case 2. \(d(u)=3\). \(T-v\) has \(p-1\) pendent vertices. Using the
assumption made in the induction, the statements of Lemma 14 and Claim 1, we have
\[\begin{aligned}
ABSC_{e}\left(T\right)= &
ABSC_{e}\left(T-v\right)+\sqrt{1-\frac{2}{e_{T}(v)+e_{T}(u)}}\\
\leq&
ABSC_{e}\left(T-v\right)+\sqrt{1-\frac{2}{2d(T)-1}}\\
\leq& q\left(n-1, p-1\right)+
\sqrt{1-\frac{2}{2n-2p+1}}=q\left(n, p\right),
\end{aligned}\] the equality is true if and only if \(T\in\mathcal{T}_{n,p}^{*}\). ◻
In this paper, we obtained some sharp upper and lower bounds for \(ABSC_{e}\) index of graphs, based on the order, size, diameter, and radius. We have also identified and described the graphs that achieve these bounds. In addition, we determined the upper and lower bounds of the \(ABSC_{e}\) index for trees, considering various graph parameters such as matching numbers or the number of pendent vertices.