Faces in graphs play a crucial role in understanding the structural properties of planar graphs. They represent the regions or bounded areas formed by the edges of the graph when it is embedded in the plane. The concept of faces provides insights into the connectivity and layout of systems, helping analyze the geometry and topology of networks, communication systems, and various real-world applications. In graph theory, the concept of resolvability plays a significant role in identifying distinct elements within a graph based on distances. In graph theory, the concept of resolvability plays a significant role in identifying distinct elements within a graph based on distances. Let \( G \) be a connected planar graph with vertex \( V(G) \), edge set \( E(G) \), and face set \( F(G) \). The distance between a face \( f \) and a vertex \( v \) is defined as the minimum distance from \( v \) to any vertex incidence to \( f \). In this work, we introduce a new resolvability parameter for connected planar graphs, referred to as the face metric dimension. A face-resolving set \( R \subseteq V(G) \) is a set of vertices such that for every pair of distinct faces \( f_1, f_2 \in F(G) \), there exists at least one vertex \( r \in R \) for which the distances \( d(f_1, r) \) and \( d(f_2, r) \) are distinct. The face metric dimension of \( G \), denoted \( \ fmd(G) \), is the minimum cardinality of a face-resolving set. This new metric provides insight into the structure of planar graphs and offers a novel perspective on the analysis of graph resolvability.
Graph theory is the branch of mathematics that deals with graphs, mathematical structures used to model pairwise relations between objects. A graph includes vertices (points) and edges (connections among objects). This framework is widely applied in computer science, biology, chemistry, and other fields. For example, in networks, vertices constitute entities like people or towns, while edges represent relationships like friendships or roads. By analyzing the structure and properties of graphs, we can remedy problems including shortest route calculations, community optimization, and molecular systems in chemistry. In terms of graph properties, the metric dimension of a graph is a measure of how well the vertices of the graph may be uniquely recognized by way of their distances to a selected subset of vertices of the graph, known as a resolving set. The edge metric dimension extends this concept to edges, where a set of vertices is chosen so that every edge in the graph can be uniquely identified by the distances from the vertices in this set to the endpoints of the edge [1]. In graph theory, the concept of the resolving set arises from the need to uniquely pick out vertices in a graph primarily based on their distances to a particular subset of vertices. A resolving set for a graph \(G\) is a subset of vertices \(S \subseteq V(G)\) such that every vertex in \(G\) is uniquely determined by way of its vector of distances to the vertices in \(S\). The smallest resolving set is called a metric basis, and its cardinality is known as the metric dimension of the graph[2].
The origins of the metric dimension hint again to the work of Slater in 1975 [3], who introduced the concept while analyzing finding units in the context of conversation networks. Around the same time, Harary and Melter independently explored the belief under the term metric dimension [4], focusing on its mathematical homes and applications. The study of metric dimension has grown notably through the years, with applications spanning community design, robot navigation, and bioinformatics. Variants just like the edge metric dimension, where edges are resolved in place of vertices, increase the framework to deal with more specialised issues, together with tracking infrastructure or analyzing chemical substances [5]. These concepts are in particular useful in regions where distinguishing structural components is crucial for optimization or type.
The metric dimension has been extensively researched and has numerous real-world applications that motivate academics. Indeed, the metric dimension is employed to determine similar patterns of a wide range of medications [6]. Other applications of metric dimensions include robot navigation [7], and combinatorial optimization [8, 9]. Computer networks [10], location issues, Sonar, and the Coast Guard, pharmaceutical chemistry [11], and canonically labeling graphs [12]. The coding and decoding of the mastermind game is covered in [13], Loran [3], honeycomb rhombic torus vertex-edge based resolvability parameters, and its application in robot navigation [14], use of resolvability parameter in city development [15]. See [16–18] for additional information on partition dimensions.
Metric dimensions have significant applications and are present in the literature. Crystal cubic carbon structure for metric dimension determined in [19], Convex polytopes graph discussion was given in [20], edge metric dimension of Cayley graphs, barycentric subdivision was completed in [21]. Metric dimension of \(VC_{4}C_{7}\) nanotubes and H-Naphtalenic nano-tubes studied in [22]. The double metric dimension of the nanotube and double edge metric dimension of the nanosheet are discussed by [23, 24]. The resolvability of aromatic hydrocarbons is present in [25], structural analysis of octagonal nanotubes discussed in [26], and the metric dimension of hexagonal cellular networks and hexagonal Möbius ladder are discussed in [27, 28]. Recently, a novel resolvability parameter was studied by [29], and double resolvability Parameters of Fosmidomycin anti-malaria drug and exchange properties are discussed by [30]. [31] discussed resolving a set of silicate metric dimensions of upper bonds of cellulose networks determined in [32], metric dimension of symmetric graphs obtained by rooted product [33], fault-tolerance and unique identification of vertices and edges in a graph: The fault-tolerant mixed metric dimension discussed by [34] The local edge partition dimension is introduced by [35]. Because of its variety, the concept of metric dimension is applied to many challenging problems. We consult [36– 38] for resolvability metrics of different chemical structures. Literature about some other resolvability parameters and uses of graphs in other fields.
Some more references about literature, constant time calculation of the metric dimension of the join of path graphs discussed by [39], dicesion making discussion by [40], metric dimensions of bicyclic graphs with potential applications in supply chain logistics present in [41], concrete crack segmentation based on UAV-enabled edge computing by [42], the mixed metric dimension and exchange property calculated by [43], fault tolerant metric dimensions of leafless cacti graphs with application studied by [44].
In graph theory, the idea of faces is essential, especially in planar graphs and their applications in topology, geometry, and community analysis. Jamil et al. introduced the face index of a graph and used the faces in predicting some physical properties of benzenoid hydrocarbons [45]. A face is a region bounded with the aid of edges in a planar embedding, such as the infinite outer face. Faces play a pivotal role in determining graph planarity and are essential to Euler’s formula \(F+V=E+2\), which relates vertices, edges, and faces in linked planar graphs. They are also essential in constructing dual graphs, in which every face corresponds to a vertex within the twin, enabling deeper topological insights. Faces discover applications in geometric networks, representing areas in maps, circuit designs, and tiling troubles, even as additionally being primary to graph coloring issues, just like the four color theorem. Additionally, they impact glide and connectivity in planar networks and are applied in optimization algorithms, which include the ones for shortest paths and planar graph drawing. In polyhedral graph theory, faces correspond to the surfaces of 3D shapes, bridging the graph idea and computational geometry. Through their numerous programs, the study of faces enhances our knowledge of graph systems and their sensible implementations in technological know-how and engineering. There are three components of the graph as vertices, edges, and faces. The resolvability based on vertices was introduced in 1975 by P. J. Slater [3], and edge-based resolvability started in 2018 by Aleksander [5]. Now we talk about the third component, face, and want to introduce a new resolvability face metric dimension. Here are some basic definitions about this parameter.
Let \(G=(V, E, F)\) be a graph with vertex set \(V\), edge set \(E\), and face set \(F\). In \(G\), the degree of a vertex is the total number of edges incident to that vertex. A vertex with degree one is called a pendant vertex. A cycle graph with \(n\) vertices is denoted by \(C_{n}\). A graph with no cycle and a unique cycle is called a tree and unicyclic graph, respectively. A bicyclic graph is a simple, connected graph that contains exactly two cycles. There are three types of bicyclic graphs. Theta Graph (cycles having only one common vertex), Figure-Eight Graph (cycles having at least one edge in common), and Barbell Graph (disjoint cycles). In this article, we discussed only the Theta Graph and the Figure-Eight Graph. A theta graph is formed by the union of three internally disjoint paths (or paths that do not intersect except at their endpoints) that share two common end vertices. A Figure-Eight Graph is a graph in which two cycles share exactly one common vertex.
Definition 1 (Planar graphs). A planar graph is a graph \(G = (V, E)\) that can be drawn on a plane without any edges crossing each other, except at their endpoints. The cycle graph \({C}_{n}\) is also an example of a planar graph.
Definition 2 (Faces in planar graphs). Let \(G\) be a connected planar graph with a set of vertices \(V(G)\), edges \(E(G)\), and faces \(F(G)\). A face in a planar graph is a connected region of the plane that is bounded by edges of the graph. This includes: The outer face (the unbounded region surrounding the entire graph). Inner faces (regions formed by the edges and vertices of the graph that are surrounded by the edges of the graph).
Definition 3 (The distance between a face and a vertex). The distance between a face \(f \in F(G)\) and a vertex \(v \in V(G)\), denoted \(d(f, v)\), is defined as:
\[d(f, v) = \min \{ d(u, v) \mid u \in V(f) \},\] Where \(V(f)\) is the set of vertices that form the boundary of the face \(f\), and \(d(u, v)\) is the length of a shortest path between vertices \(u\) and \(v\) in \(G\).
Definition 4 (Face-resolving set). A face-resolving set \(R \subseteq V(G)\) is a set of vertices such that for every pair of distinct faces \(f_1, f_2 \in F(G)\), there exists at least one vertex \(r \in R\) for which the distances \(d(f_1, r)\) and \(d(f_2, r)\) are distinct.
Definition 5 (Face metric dimension). The face metric dimension of \(G\), denoted as \(fmd(G)\), is the minimum cardinality of a face-resolving set \(R \subseteq V(G)\).
Example 1. With the help of an example, we explain the concept of face metric dimension.
Let \({R}=\{{a}_{1},{a}_{4},{a}_{8}\}\) be the subset of vertices of Figure 1 and their are 5 faces. We show that the representation of all faces concerning \({R},\) is unique, so \({R},\) is the face resolving set of cardinality \(3.\) The set of cardinalities \(1\) and \(2\) does not have unique representations, so the set of cardinality \(3\) is the minimum face resolving set. Hence, the face metric dimension is \(3.\)

In this section, we explore the face metric dimension of trees, unicyclic, and bicyclic graphs.
Theorem 1. The face metric dimension of the tree and unicyclic graph is \(1\) except cycle graph.
Proof. Suppose \(R\) is the subset of vertices of the tree and has cardinality one. We select any one vertex on \(T\), there is only one face that has zero distance from \(R\) and is unique. So \(R\) has the smallest cardinality, and \(R\) is a face resolving set for the tree. Hence, the face metric dimension of the tree is one. Now we talk about a unicyclic graph with pendent vertices, then there are only \(2\) faces, one is enclosed in the cycle, and the other is an external face. Let us choose any one vertex in \(R\) that does not belong to the enclosed face, so this face has a distance other than zero, and the external face has zero distance, so the distances are unique. Hence, the face metric dimension is one. Suppose we take \({C}_{n}\), then we choose any number of vertices. The representation of inner and outer faces is are same. So we can not find the face metric dimension of \({C}_{n}\). ◻
The face metric dimension of Theta, Figure-Eight bicyclic graphs with pendent vertices is \(1\) because if we select any pendent vertex, then the distances of both cycles are different, so the representations of all three faces are different. Let \({f}_{1},\) \({f}_{2}\) and \({f}_{ext}.\) The distance of \({f}_{ext}\) is zero and \({f}_{1}\) is one because the point of \(R\) is from the pendent of \({f}_{1}.\) The distance of \({f}_{2}\) to \({R}\) is \(x\) where \(x\) is the number of edges between \({f}_{2}\) and \({R}.\) If the member of \({R}\) is from \({f}_{2}\) the distance of \({f}_{2}\) is one and \({f}_{1}\) is \(x\) reason is same mention above. Hence, all distances are different, so \({R}\) is a face resolving set of cardinality one.
Theorem 1. The face metric dimension of the Theta, Figure-Eight bicyclic graph without any pendant vertices is \(2.\)
Proof. Suppose a bicyclic graph then there are only \(3\) faces \({f}_{1},\) \({f}_{2}\) and \({f}_{ext}.\) \({f}_{1}\) and \({f}_{2}\) are enclosed in cycles and \({f}_{ext}\) is an external face. Let us choose any two vertices in \(R\), each of which belongs to a different face enclosed by a cycle. Then there are three distinct presentations \((0,0)\) for \({f}_{ext},\) \((0,x)\) for \({f}_{1},\) and \((y,0)\) for \({f}_{2}.\) where \(x\) and \(y\) are the distances of both faces to selected vertices of \(R.\) The representation always \((0,x) \neq (y,0)\) either \({x}={y}\) or \({x}\neq{y}\) because \({x}\neq 0 \neq{y}.\) Suppose \({x}= 0 ={y}\) then \({x}\) and \({y}\) belong to same face or graph has one cycle. This is the contradiction of our supposition that we take the points from different cycles. So the representations are unique. ◻
In this section, we determine the face metric dimension of ladder and grid graphs, two fundamental families of planar graphs. Ladder graphs, denoted as \(L_{2n}\), consist of two parallel paths connected by rungs, while square grid graphs, denoted as \({SG}_{mn}\), form a rectangular lattice structure. Due to their structured arrangement of faces, these graphs exhibit predictable face-resolving sets.
A ladder graph, denoted as \({L}_{2n}\), is a type of graph that resembles the structure of a ladder. It consists of two parallel paths (or cycles) connected by a series of rungs.
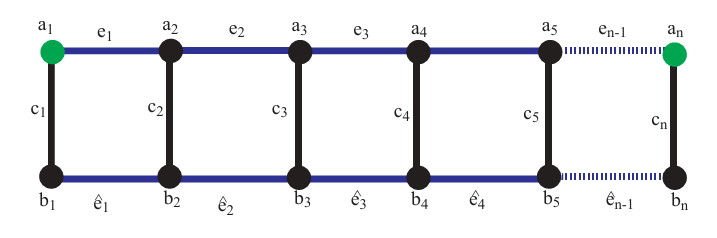
In Figure 2 \({a}_{i}, {b}_{i}\) \(3\leq {i} \leq {n}\) are the vertices and \({e}_{i}, \hat{e}_{i}\) \(2\leq {i} \leq {n-1}\) be the edges and the green vertices are the points predicted for face resolving set. In a ladder graph, the number of vertices is \(2n\) where \({n}\geq 3\) and \(3n-2\) edges. In other words the \(\vert V(L_{2n})\vert =2n\) and \(\vert E(L_{2n})\vert =3n-2.\) In a ladder graph all vertices are of degree \(3\) except corner points which have degree \(2.\) The number of vertices of degree three is \(2n-4\), and degree two vertices is \(4.\) The vertices, edges, and faces in the form of the set are represented. \[\begin{aligned} V({L}_{2n})=&\{{a}_{i},{b}_{i}; 1\leq{i}\leq {n},\},\\ E({L}_{2n})=&\{{a}_{i}{a}_{i+1},{a}_{i}{b}_{i},{b}_{i}{b}_{i+1}; 1\leq{i}\leq {n-1}\},\\ F({L}_{2n})=&\{{a}_{i}{a}_{i+1}{a}_{i+1}{b}_{i+1}{a}_{i}{b}_{i}{b}_{i}{b}_{i+1}; 1\leq{i}\leq {n}\}.\\ \end{aligned}\]
Theorem 3. Suppose \({L}_{2n}\) be a ladder graph for \({n} \geq 3,\) then the face metric dimension is \(2.\)
Proof. Assume that a subset of the vertices of \(L_{2n}\) is \({R}=\{{a}_{1},{a}_{n}\}.\) We shall demonstrate that \(R\) is a face resolving set of cardinality \(2.\) The distinct representations of all faces of \(L_{2n}\) for \({n}=5\) is present in Figure 3. The unique codes are present on each face. so \(R\) is face resolving set ofcardinality \(2\) with \({R}=\{{a}_{1},{a}_{5}\}.\)

Now we discussed in generalized case where \({R}=\{{a}_{1},{a}_{n}\}.\) In Figure 4, the representation of each face is given, and the representation of the external face is \((0,0).\) The representation is unique, so \(R\) is a face resolving set. The generalized distances of faces of ladder to \({R}=\{{a}_{1},{a}_{n}\}.\) are given below.
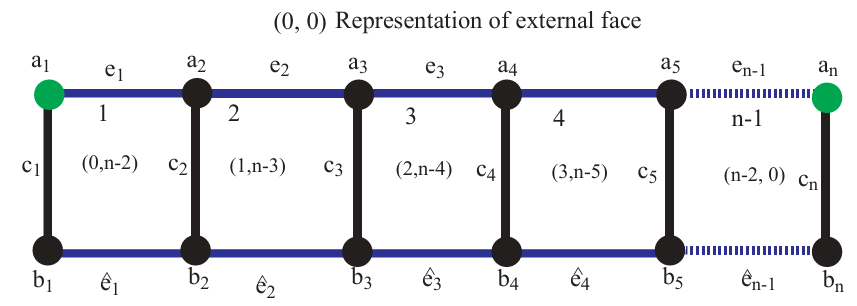
Generalized formulas of distances help us to check the unique representation of each face. The generalized distance formulas are given below. Let \({R}=\{{a}_{1},{a}_{n}\}\) and \(r(f,R)= (d(f,{a}_{1}),d(f,{a}_{n}))\) and \(d(f,{a}_{1})=min\{d({a}_{i},{a}_{1}): {a}_{i}\in f\}\), \(d(f,{a}_{n})=min\{d({a}_{i},{a}_{n}): {a}_{i}\in f\}\) \[\begin{aligned} d(f_{i},{a}_{1}) = \left\lbrace \begin{array}{ll} {i}-1 &\hbox{for}\ \ 1\leq{i}\leq {n-1}.\\ \end{array} \right.\\ d(f_{1},{a}_{n}) = \left\lbrace \begin{array}{ll} {n}-{i}-1 &\hbox{for} \ \ 1\leq{i}\leq {n-1}.\\ \end{array} \right. \end{aligned}\]
\((0,0)\) is the representation of an external face. All Faces have unique representation, so \(R\) is a face resolving set of cardinality \(2.\) It is the minimum cardinality of \(R\) because a singleton set does not have a unique representation. Suppose we take any point on a ladder graph, then the representation of the external face and adjacent face of that point has the same distance \(0\), so a singleton is not possible in the case of the ladder. Hence, prove that the face metric dimension of the ladder graph is \(2.\) ◻
A grid graph is a type of graph that represents a two-dimensional grid structure, where vertices are arranged in a rectangular or square lattice, and edges connect adjacent vertices. In Figure 5 \({a}_{i,j}\) are the vertices and \({e}_{i,j}\) are the edges, and the green vertices are the points of the face resolving set. In a grid graph the number of vertices are \({m}{n}\) where \({m,n}\geq 2\) and \(2{m}{n}-{m}-{n}\) edges.The faces in a grid graph are \((m-1)(n-1)+1.\) In other words the \(\vert V(S{SG}_{mn})\vert ={m}{n},\) \(\vert E(S{SG}_{mn})\vert =2{m}{n}-{m}-{n}.\) THe number of faces in a grid graph are \({m}{n}-{m}-{n}+2.\) In a grid graph, the vertices of degree \(2\) are corner points, and all other vertices are of degree \(3\) or \(4.\) The vertices, edges, and faces in the form of the set are represented. \[\begin{aligned} V({SG}_{mn})=&\{{a}_{i,j}; 1\leq{i}\leq {m}, 1\leq{j}\leq {n}\},\\ E({SG}_{mn})=&\{{a}_{i,j}{a}_{i+1,j},{a}_{i,j}{a}_{i,j+1}; 1\leq{j}\leq {m-1}, 1\leq{j}\leq {n-1}\},\\ F({SG}_{mn})=&\{{a}_{i,j}{a}_{i+1,j}{a}_{i,j}{a}_{i,j+1}{a}_{i+1,j+1}{a}_{i+1,j}{a}_{i,j}{a}_{i,j+1}; 1\leq{i}\leq {n},1\leq{j}\leq {m}\}. \end{aligned}\]
The face metric dimension of a grid graph is an exploration into how the concept of the face metric dimension applies to grid graphs, which are commonly used in graph theory to represent regular lattice structures. In this section, we discuss how the face metric dimension refers to a specific way of measuring the “distance” between the faces (or regions) of a grid graph about a particular set of vertices. This dimension can provide insights into the topological properties and efficiency of the graph in terms of covering and distance optimization.
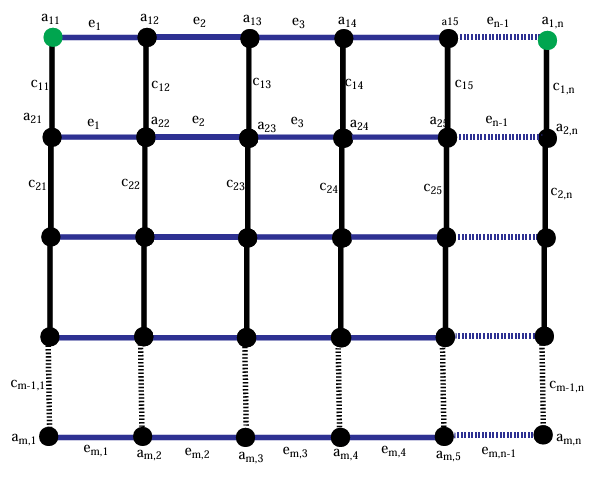
Theorem 4. Suppose \({SG}_{mn}\) be a grid graph for \({m}, {n} \geq2,\) and \({m}\neq{n} =2,\) then the face metric dimension is \(2.\)
Proof. Assume that a subset of the vertices of \({SG}_{mn}\) is \({R}=\{{a}_{11},{a}_{1,n}\}.\) We shall demonstrate that \(R\) is a face resolving set of cardinality \(2.\) The distinct representations of all faces for \({m}=2,{n}=3\) or \({m}=3,{n}=2\) is unique from ladder case. The unique representation of \({SG}_{mn}\) for \({m}=3={n}\) is present in Figure 6, the codes are present in each face. so \(R\) is face resolving set ofcardinality \(2\) with \({R}=\{{a}_{11},{a}_{13}\}.\)

Now we discuss two cases in which \({m}\neq{n}\) where \({R}=\{{a}_{11},{a}_{14}\}.\) We assign a number to each face to make generalized formulas of distances of all faces to points of the resolving set. In Figure 4 the representation of each face in unique so \(R\) is face resoling set of cardinality \(2\) with \({R}=\{{a}_{11},{a}_{1,n}\}.\)

In Figure 7 \((a)\) and \((b)\) the codes are present in faces and all are unique so \(R\) is face resolving set of cardinality \(2\) with different vertices as \({R}=\{{a}_{11},{a}_{14}\}\) for Figure 7(a) and \({R}=\{{a}_{11},{a}_{13}\}\) for Figure 7(b) but the cardinality remain constant. Now we discuss the general case in which \((m-1)(n-1)\) faces are present.

In Figure 8, the code of each face is present and all are unique, so \(R\) is a face resolving set of cardinality \(2\) with vertices \({R}=\{{a}_{11},{a}_{1,n}\}.\) Now we discuss general formulas of distances for all faces to \(R.\) Generalized formulas of distances help us to check the unique representation of each face. The generalized distance formulas are given below. Let \({R}=\{{a}_{11},{a}_{1,n}\}\) and \(r(f,R)= (d(f,{a}_{11}),d(f,{a}_{1,n}))\) and \(d(f,{a}_{11})=min\{d({a}_{i,j},{a}_{11}): {a}_{i,j}\in V(f)\}\), \(d(f,{a}_{1,n})=min\{d({a}_{i,j},{a}_{1,n}): {a}_{i,j}\in V(f)\}\) \({i}\) and \({j}\) changes with \({m}\) and \({n}.\) \[\begin{aligned} d(f_{i},{a}_{11}) = \left\lbrace \begin{array}{ll} {i}+{j}-2 &\hbox{for}\ \ 1\leq{i}\leq {m-1}, \ 1\leq{j}\leq {n-1}.\\ \end{array} \right.\\ d(f_{i},{a}_{1,n}) = \left\lbrace \begin{array}{ll} {n}+{i}-{j}-2 &\hbox{for} \ \ 1\leq{i}\leq {m-1}, \ 1\leq{j}\leq {n-1}.\\ \end{array} \right. \end{aligned}\]
\((0,0)\) is the representation of an external face. All Faces have unique representation, so \(R\) is a face resolving set of cardinality \(2.\) It is the minimum cardinality of \(R\) because a singleton set does not have a unique representation. Suppose we take any vertex on a grid graph, then the representation of its neighbour faces has the same distance \(0\), so a single vertex is not possible in the case of a grid graph. Hence, prove that the face metric dimension of the grid graph is \(2.\) ◻
Scenario: In an urban setting, homes (vertices) are surrounded by streets (edges), forming city blocks (faces). A surveillance system or emergency response monitoring system could use the concept of the face metric dimension to optimize resource placement.
Definition of the Problem: Each city block is treated as a face in the graph. To ensure the best surveillance or response coverage, we aim to identify a minimal set of homes (vertices) such that their distances to all streets (faces) are unique. This guarantees that any event in a particular block can be uniquely identified based on proximity data to the monitored homes.
Practical Setup: Place surveillance cameras or emergency response devices at the selected homes corresponding to the face-resolving set. These devices can record or alert based on unique distance measures to surrounding blocks. Benefits:
Optimal Coverage: Minimizes the number of devices needed while maintaining unique identification of events for all blocks. Efficient Response: Ensures faster identification and resolution of issues in specific city blocks.
Extensions: This approach can be expanded to urban planning for placing service stations, utilities, or monitoring points to ensure efficient coverage with minimal resources.
In this article, we introduced a novel concept of the face Metric Dimension as a new resolvability parameter in graph theory. We applied the face metric dimension to two wonderful graph ladders and grid graphs, each of that have the face metric dimension \(2.\) In addition, validating its utility throughout distinctive topologies. The capacity to uniquely identify blocks primarily based on distance signatures guarantees clearer responsibility zones and greater green provider in urban control tasks. Additionally, by applying this idea to urban situations, mainly in the Smart Town Rubbish Series, we validated its ability to optimize aid allocation and enhance efficiency. Through the identity of face-resolving units, we confirmed how minimal sensor placement can make certain precise tracking of each block, lowering expenses at the same time as keeping powerful garbage collection monitoring. This study highlights the practical importance of graph-theoretic parameters in solving real-world problems and opens the door for destiny exploration in other smart metropolis packages, consisting of traffic tracking, utility distribution, and emergency reaction systems. The face metric measurement presents a powerful device for reinforcing city planning and optimizing aid utilization, ensuring that smart cities can perform greater sustainably and efficaciously.
Problem 1. How can we calculate the face edge metric dimension and the face mixed metric dimension?
The author(s) would like to express their sincere gratitude to the Department of Mathematics, Riphah International University, Lahore, for providing the resources, support, and an inspiring research environment that greatly contributed to the completion of this study.
Special thanks to colleagues, mentors, and peers for their valuable insights and encouragement throughout this research journey.
All the data supporting the results are included in the manuscript.
West, D. B. (2001). Introduction to Graph Theory (Vol. 2). Upper Saddle River: Prentice Hall. M.
Azeem, Cycle-super magic labeling of polyomino linear and zig-zag chains. Journal of Operations Intelligence 1.1(2023): 67-81. https://doi.org/10.31181/jopi1120235.
Slater, P. J. (1975). Leaves of trees. Congressus Numerantium, 14, 549-559.
Harary, F., & Melter, R. A. (1976). On the metric dimension of a graph. Ars Combinatoria, 2, 191-195.
Kelenc, A., Tratnik, N., & Yero, I. G. (2018). Uniquely identifying the edges of a graph: the edge metric dimension. Discrete Applied Mathematics, 251, 204-220.
Johnson, M. (1993). Structure-activity maps for visualizing the graph variables arising in drug design. Journal of Biopharmaceutical Statistics, 3(2), 203-236.
Khuller, S., Raghavachari, B., & Rosenfeld, A. (1996). Landmarks in graphs. Discrete Applied Mathematics, 70(3), 217-229.
Sebő, A., & Tannier, E. (2004). On metric generators of graphs. Mathematics of Operations Research, 29(2), 383-393.
Ahmad, A., Koam, A. N., Siddiqui, M. H. F., & Azeem, M. (2022). Resolvability of the starphene structure and applications in electronics. Ain Shams Engineering Journal, 13(2), 101587.
Manuel, P., Bharati, R., & Rajasingh, I. (2008). On the minimum metric dimension of honeycomb networks. Journal of Discrete Algorithms, 6(1), 20-27.
Chartrand, G., Eroh, L., Johnson, M. A., & Oellermann, O. R. (2000). Resolvability in graphs and the metric dimension of a graph. Discrete Applied Mathematics, 105(1-3), 99-113.
Piperno, A. (2008). Search space contraction in canonical labeling of graphs. arXiv preprint arXiv:0804.4881.
Chvátal, V. (1983). Mastermind. Combinatorica, 3, 325-329.
Bukhari, S., Jamil, M. K., Azeem, M., & Swaray, S. (2024). Honeycomb rhombic torus vertex-edge based resolvability parameters and their application in robot navigation. IEEE Access, 12, 23751-23757.
Ali, S., & Jamil, M. K. (2024). Exchange property in double-edge resolving partition sets and their use in city development. Spectrum of Decision Making and Applications, 1(1), 84-97.
Koam, A. N., Ahmad, A., Azeem, M., & Nadeem, M. F. (2022). Bounds on the partition dimension of one pentagonal carbon nanocone structure. Arabian Journal of Chemistry, 15(7), 103923.
Nawaz, R., Jamil, M. K., Asmat, F., Azeem, M., & Almohsen, B. (2024). A novel application for computing the partition dimension of the subdivision of a circulant network. IEEE Access. 10.1109/ACCESS.2024.3443084
Bhatti, R., Jamil, M. K., Azeem, M., & Poojary, P. (2024). Partition dimension of generalized hexagonal cellular networks and its application. IEEE Access, 12, 12199-12208.
Zhang, X., & Naeem, M. (2021). The metric dimension of crystal cubic carbon crystal structure. Journal of Mathematics, 2021(1), 3438611.
Ahsan, M., Zahid, Z., Zafar, S., Rafiq, A., Sindhu, M. S., & Umar, M. (2021). Computing the edge metric dimension of convex polytopes related to graphs. Journal Mathematics Computer Science, 22(2), 174-188.
Koam, A. N., & Ahmad, A. (2020). Barycentric subdivision of Cayley graphs with constant edge metric dimension. IEEE Access, 8, 80624-80628.
Siddiqui, M. K., & Imran, M. (2015). Computing the metric and partition dimension of H-Naphtalenic and VC5C7 nanotubes. Journal of Optoelectronics and Advanced Materials, 17(5-6), 790-794.
Koam, A. N., Ali, S., Ahmad, A., Azeem, M., & Jamil, M. K. (2023). Resolving the set and exchange property in a nanotube. AIMS Mathematics, 8(9), 20305-20323.
Koam, A. N., Ahmad, A., Ali, S., Jamil, M. K., & Azeem, M. (2024). Double-edge resolving set and exchange property for the nanosheet structure. Heliyon, 10(5), e26992.
Azeem, M., & Nadeem, M. F. (2021). Metric-based resolvability of polycyclic aromatic hydrocarbons. The European Physical Journal Plus, 136(4), 1-14.
Alali, A. S., Ali, S., & Jamil, M. K. (2024). Structural analysis of octagonal nanotubes via double edge-resolving partitions. Processes, 12(9), 1920.
Azeem, M., Imran, M., & Nadeem, M. F. (2022). Sharp bounds on the partition dimension of the hexagonal Möbius ladder. Journal of King Saud University-Science, 34(2), 101779.
Azeem, M., Jamil, M. K., & Shang, Y. (2023). Notes on the localization of generalized hexagonal cellular networks. Mathematics, 11(4), 844.
Ali, S., Azeem, M., Zahid, M. A., Usman, M., & Pal, M. (2024). Novel resolvability parameter of some well-known graphs and exchange properties with applications. Journal of Applied Mathematics and Computing, 70(5), 4373-4394.
Ismail, R., Ali, S., Azeem, M., & Zahid, M. A. (2024). Double resolvability parameters of fosmidomycin anti-malaria drug and exchange property. Heliyon, 10(13), e33211.
Raj, F. S., & George, A. (2015). On the metric dimension of silicate stars. Arpn Journal of Engineering and Applied Sciences, 10(5), 2187-2192.
Imran, S., Siddiqui, M. K., & Hussain, M. (2019). Computing the upper bounds for the metric dimension of the cellulose network. Applied Mathematics E-Notes, 19, 585-605.
Imran, S., Siddiqui, M. K., Imran, M., & Hussain, M. (2018). On metric dimensions of symmetric graphs obtained by the rooted product. Mathematics, 6(10), 191.
Khan, A., Ali, S., Hayat, S., Azeem, M., Zhong, Y., Zahid, M. A., & Alenazi, M. J. (2025). Fault-tolerance and unique identification of vertices and edges in a graph: The fault-tolerant mixed metric dimension. Journal of Parallel and Distributed Computing, 197, 105024.
Ali, S., & Jamil, F. A. M. K. The novel resolvability parameter, local edge partition dimension of graphs. Open Journal of Discrete Applied Mathematics (ODAM), 7(3), 69-71.
Hussain, Z., Munir, M., Chaudhary, M., & Kang, S. M. (2018). Computing metric dimension and metric basis of the 2D lattice of alpha-boron nanotubes. Symmetry, 10(8), 300.
Krishnan, S., & Rajan, B. (2016). Fault-tolerant resolvability of certain crystal structures. Applied Mathematics, 7(7), 599-604.
Ahmad, A., Bača, M., & Sultan, S. (2020). Computing the metric dimension of the kayak paddles graph and cycles with the chord. Proyecciones (Antofagasta), 39(2), 287-300.
Zhang, C., Haidar, G., Khan, M. U. I., Yousafzai, F., Hila, K., & Khan, A. U. I. (2023). Constant-time calculation of the metric dimension of the join of path graphs. Symmetry, 15(3), 708.
Liu, P., Asim, M. H., Ali, S., Azeem, M., & Almohsen, B. (2024). Utilizing the lexicographic max product of the picture fuzzy graph in human trafficking. Ain Shams Engineering Journal, 15(11), 103009.
Khan, A., Haidar, G., Abbas, N., Khan, M. U. I., Niazi, A. U. K., & Khan, A. U. I. (2023). Metric dimensions of bicyclic graphs. Mathematics, 11(4), 869.
Yang, J., Li, H., Zou, J., Jiang, S., Li, R., & Liu, X. (2022). Concrete crack segmentation based on UAV-enabled edge computing. Neurocomputing, 485, 233-241.
Liu, P., Ali, S., Azeem, M., Kamran Jamil, M., Zahid, M. A., Ali, W., & Almohsen, B. (2024). Mixed metric dimension and exchange property of hexagonal nano-network. Scientific Reports, 14(1), 26536.
Asif, T., Haidar, G., Yousafzai, F., Khan, M. U. I., Khan, Q., & Fatima, R. (2024). Fault Tolerant Metric Dimensions of Leafless Cacti Graphs with Application in Supply Chain Management. arXiv preprint arXiv:2409.12199.
Kamran, M., Imran, M., & Sattar, K. A. (2020). Novel face index for benzenoid hydrocarbons. Mathematics, 8(3), 312. https://doi.org/10.3390/math8030312
