A note on marginal entropy of graphs

1. Introduction

Entropy was originally a concept in statistical physics. In 1948, Shannon first extended this concept to the process of channel communication [1], thus creating the discipline of “information theory”. The concept of graph entropy was defined by Rashevsky in 1955 for studying the relations between the topological properties of graphs and their information content [2]. In fact, topological index is topological invariant derived from molecular graphs of compounds [3], which establishes the relationship between the structure and properties of the molecule. The first topological index was introduced in 1947 by Wiener [4], and was initially used for modelling boiling points of alkane molecules.

Let \(G\) be a simple undirected graph with vertex set \(V(G)\) and edge set \(E(G)\). The distance \(d_G(u,v)\) between two vertices \(u\), \(v\) of \(G\) is the length of a shortest \((u,v)\)-path in \(G\). The Wiener index of a graph \(G\) is defined as \[W(G)=\frac{1}{2}\sum_{u\in V(G)}{D_G(u)},\] where \(D_G(u)=\sum_{v\in V(G)}{d_G(u,v)}\) is the total distance of vertex \(u\). It remains, to this day, one of the most popular and widely studied topological indices in mathematical chemistry.

In subsequent studies, scholars have proposed many topological indices, such as the Randic index [5], the Zagreb indices [6,7], the atom-boud connectivity index [8] and so on. Hundreds of different topological indices have been applied to QSAR (quantitative structure-activity relationship)/QSAR (quantitative structure-property relationship) modelings. Besides, they are also used for the discrimination of isomers [9], which is significant for the coding and the computer processing of chemical structures. In 1977, Bonchev and Trinajstic [10] introduced an molecular entropy measure based on distances, which is also called information indices, to interpret the molecular branching. They found that the information indices have greater ability for discrimination between isomers than those topological indices based on adjacency, incidence or polynomial coefficients of adjacency matrix. Dehmer et al., [11] introduced Hosoya entropy in 2014. In 2015, Mowshowitz and Dehmer [12] established the connections between the information content of a graph and Hosoya entropy. For more research in this area, readers can refer to the paper [13].

Base on the previous research, Konstantinova [14] proposed the marginal entropy of a graph \(G\) as follows:

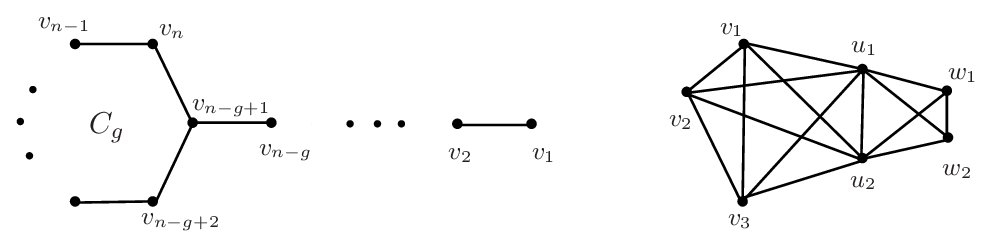
\begin{eqnarray*} I_D(G) &=& -\sum_{u\in V(G)}{\frac{D_G(u)}{\sum_{u\in V(G)}{D_G(u)}}\log_{2}{\frac{D_G(u)}{\sum_{u\in V(G)}{D_G(u)}}}} \end{eqnarray*}\begin{eqnarray*} &=& 1+\log_{2}{W(G)}-\frac{1}{2W(G)}\sum_{u\in V(G)}{D_G(u)\log_{2}{D_G(u)}}\\ & = & -\frac{1}{\sum_{u\in V(G)}{D_G(u)}}\sum_{u\in V(G)}{D_G(u)}\log_{2}{D_G(u)}+\log_{2}{\sum_{u\in V(G)}{D_G(u)}}. \end{eqnarray*} In 2021, Sahin [15] obtained the marginal entropy of paths, stars, double stars, cycles and vertex-transitive graphs. On this basis, we give the quantitative calculation formula of marginal entropy for the complete bipartite graphs, complete multipartite graphs, firefly graphs, lollipop graphs, clique-chain graphs, Cartesian product and join of two graphs, which extends the results of Sahin.

2. Preliminaries

We first introduce several special kinds of graphs. Defined by Aouchiche et al., [16], a firefly graph \(F_{s,t,n-2s-2t-1}\) (\(s\geq 0\), \(t\geq 0\), \(n-2s-2t-1\geq 0\)) is a graph of order \(n\) that consists of \(s\) triangles, \(t\) pendent paths of length 2 and \(n-2s-2t-1\) pendent edges, sharing a common vertex. The lollipop graph \(C_{n,g}\) (shown in Figure 1), first used in [17], is obtained by attaching a vertex of cycle \(C_g\) to an end vertex of path \(P_{n-g-1}\). The class of clique-chain graphs \(G_d(a_1,a_2,\ldots,a_d,a_{d+1})\) is composed of \(d+1\) cliques \(K_{a_1}\), \(K_{a_2}\), …, \(K_{a_{d}}\), \(K_{a_{d+1}}\), where \(n_i\geq 1\) for \(1\leq i\leq d+1\) and \(\sum_{1\leq i\leq d+1}a_i=n\), the edges between two adjacent cliques is full. The graph \(G_2(3,2,2)\) (shown in Figure 1) is an example. Obviously, the diameter of clique-chain graph \(G_d\) is \(d\).

Definition 1. For two simple graphs \(G_1\) and \(G_2\), the Cartesian product \(G_1\square G_2\) of them is defined with vertex set \(V(G_1\square G_2)=V(G_1)\times V(G_2)\) and edge set \(E(G_1\square G_2)=\big\{uv,u=(u_1,v_1),v=(u_2,v_2) \big|[u_1=u_2 \ and \ v_1v_2\in E(G_2)] \ or \ [v_1=v_2 \ and \ u_1u_2\in E(G_1)] \big\}\).

Definition 2. For two simple graphs \(G_1\) and \(G_2\), the join \(G_1\vee G_2\) of them is defined with vertex set \(V(G_1\vee G_2)=V(G_1)\cup V(G_2))\) and edge set \(E(G_1\vee G_2)=E(G_1)\cup E(G_2)\cup \big\{uv\big|u\in V(G_1),v\in V(G_2)\big\}\).

Lemma 1.([18]) Let \(G=G_1\square G_2\), for two vertices \(u=(u_1,v_1)\) and \(v=(u_2,v_2)\) of \(G\), where \(u_i\in V(G_1),v_i\in V(G_2)\), \(i=1,2\). Then we have \(d_G(u,v)=d_{G_1}(u_1,u_2)+d_{G_2}(v_1,v_2)\).

3. Main results

First, we consider the complete bipartite graph \(K_{a,b}\).

Theorem 1. The marginal entropy of the complete bipartite graph \(K_{a,b}\) is given by the following formula \[I_D(K_{a,b})=1-\frac{\log_{2}{\Big[(2a+b-2)^{(2a^2+ab-2a)}(2b+a-2)^{(2b^2+ab-2b)}\Big]}}{2a^2+2b^2+2ab-2a-2b}+\log_{2}{(a^{2}+b^{2}+ab-a-b)}.\]

Proof. Let \(A\) and \(B\) be the parts of \(K_{a,b}\) with \(a\), \(b\) vertices, respectively. We have,

• \(D_{K_{a,b}}(u)=b+2(a-1)=2a+b-2\) for \(u\in A\),
• \(D_{K_{a,b}}(u)=a+2(b-1)=2b+a-2\) for \(u\in B\).

By the definition of the marginal entropy, \(I_D(K_{a,b})\) can be computed as, \begin{eqnarray*} I_D(K_{a,b}) &=&-\frac{1}{\sum_{u\in V(K_{a,b})}{D(u)}}\sum_{u\in V(K_{a,b})}{D(u)}\log_{2}{D(u)}+\log_{2}{\sum_{u\in V(K_{a,b})}{D(u)}} \\ \nonumber &=& -\frac{1}{a(2a+b-2)+b(2b+a-2)}\Big[\sum_{u\in A}\big((2a+b-2)\log_{2}(2a+b-2)\big)+\sum_{u\in B}\big((2b+a-2)\log_{2}(2b+a-2)\big)\Big]\\ \nonumber & & +\log_{2}{\big(a(2a+b-2)+b(2b+a-2)\big)}\\ \nonumber &=& -\frac{1}{2a^2+2b^2+2ab-2a-2b}\Big[a\big((2a+b-2)\log_{2}(2a+b-2)\big)+b\big((2b+a-2)\log_{2}(2b+a-2)\big)\Big]\\ \nonumber & &+\log_{2}{(2a^2+2b^2+2ab-2a-2b)}\\ \nonumber &=& -\frac{1}{2a^2+2b^2+2ab-2a-2b}\Big[{(2a^2+ab-2a)\log_{2}{(2a+b-2)}}+{(2b^2+ab-2b)\log_{2}{(2b+a-2)}}\Big]\\ \nonumber & &+\log_{2}{\big(2(a^2+b^2+ab-a-b)\big)}\\ \nonumber &=& 1-\frac{\log_{2}{\Big[(2a+b-2)^{(2a^2+ab-2a)}(2b+a-2)^{(2b^2+ab-2b)}\Big]}}{2a^2+2b^2+2ab-2a-2b}+\log_{2}{(a^{2}+b^{2}+ab-a-b)}. \end{eqnarray*} This completes the proof.

As a generalization, we have the following result. Since bipartite graph is also special multipartite graph, when \(a_i=0\) holds for \(i\geq3\) in Theorem 2, one can get the result of Theorem 1 from Theorem 2 by simply deduction.

Theorem 2. The marginal entropy of the complete multipartite graph \(K_{a_1,a_2,\ldots,a_k}\) is given by the following formula \[I_D(K_{a_1,a_2,\ldots,a_k})=-\frac{\sum_{i=1}^{k}{\big(n+a_i-2\big)\log_{2}\big(n+a_i-2\big)}}{n^2-2n+\sum_{i=1}^{k}a_i^2}+\log_{2}{\big[n^2-2n+\sum_{i=1}^{k}a_i^2\big]}.\]

Proof. Let \(V_i\) be the part of \(K_{a_1,a_2,\ldots,a_k}\) with \(a_i\) vertices. Then for \(u\in V_i\) \[D(u)=a_1+a_2+\ldots+a_{i-1}+a_{i+1}+\ldots+a_k+2(a_i-1)=n-a_i+2(a_i-1)=n+a_i-2.\] Therefore, we have \[\sum_{u\in V(K_{a_1,\ldots,a_k})}D(u)=\sum_{i=1}^{k}a_i(n+a_i-2)=n^2-2n+\sum_{i=1}^{k}a_i^2.\] By definition of marginal entropy, \(I_D(K_{a_1,a_2,\ldots,a_k})\) can be computed as \begin{eqnarray*} I_D(K_{a_1,\ldots,a_k}) &=&-\frac{1}{\sum_{u\in V(K_{a_1,\ldots,a_k})}{D(u)}}\sum_{u\in V(K_{a_1,\ldots,a_k})}{D(u)}\log_{2}{D(u)}+\log_{2}{\sum_{u\in V(K_{a_1,\ldots,a_k})}{D(u)}} \\ \nonumber &=& -\frac{\sum_{i=1}^{k}{\big(n+a_i-2\big)\log_{2}\big(n+a_i-2\big)}}{n^2-2n+\sum_{i=1}^{k}a_i^2}+\log_{2}{\big[n^2-2n+\sum_{i=1}^{k}a_i^2\big]}. \end{eqnarray*} This completes the proof.

In the next, we present the calculation formulas of the marginal entropy for firefly graph, lollipop graph and clique-chain graph by giving a specific vertex set partition to them respectively.

Theorem 3. The marginal entropy of the \(n\)-vertex firefly graph \(F_{s,t,n-2s-2t-1}\) is given by the following formula, \begin{eqnarray*} I_D(F_{s,t,n-2s-2t-1}) &=& 1-\frac{1}{2(n^2-2n-s-3t+tn+1)}\Big[(n+t-1)\log_2(n+t-1)+2s(2n+t-4)\log_2(2n+t-4)\\ & & +(n-2s-2t-1)(2n+t-3)\log_2(2n+t-3)\Big]+t(3n+t-7)\log_2(3n+t-7)\\ & &+t(2n+t-5)\log_2(2n+t-5)+\log_2(n^2-2n-s-3t+tn+1). \end{eqnarray*}

Proof. First, denote the unique vertex with maximum degree \(n-t-1\) by \(u_0\), we partition the rest vertices of \(F_{s,t,n-2s-2t-1}\) as following:

• \(A\): the set of all the vertices in triangles,
• \(B\): the set of pendent vertex \(x\) such that \(d(x,u_0)=1\),
• \(C\): the set of pendent vertex \(x\) such that \(d(x,u_0)=2\),
• \(D=V(F_{s,t,n-2s-2t-1}) \backslash \big(A\cup B\cup C\cup\{u_0\}\big)\).

According to the definition of firefly graph, \(|A|=2s\), \(|B|=n-2s-2t-1\), \(|C|=t\), \(|D|=t\) and \(|A|+|B|+|C|+|D|+1=n\). By direct calculation, \(D(u_0)=n+t-1\); for \(u\in A\), \(D(u)=2n+t-4\); for \(u\in B\), \(D(u)=2n+t-3\); for \(u\in C\), \(D(u)=3n+t-7\); for \(u\in D\), \(D(u)=2n+t-5\). Therefore, we have \begin{eqnarray*} \sum_{u\in V(F_{s,t,n-2s-2t-1})}D(u)&=&(n+t-1)+2s(2n+t-4)+(n-2s-2t-1)(2n+t-3)+t(3n+t-7)+t(2n+t-5)\\ &=& 2n^2-4n-2s-6t+2tn+2\,, \end{eqnarray*} and then \begin{eqnarray*} I_D(F_{s,t,n-2s-2t-1}) &=& -\frac{1}{2n^2-4n-2s-6t+2tn+2}\Big[(n+t-1)\log_2(n+t-1)+2s(2n+t-4)\log_2(2n+t-4)\\ & & +(n-2s-2t-1)(2n+t-3)\log_2(2n+t-3)\Big]+t(3n+t-7)\log_2(3n+t-7)\\ & & +t(2n+t-5)\log_2(2n+t-5)+\log_2(2n^2-4n-2s-6t+2tn+2)\\ &=& 1-\frac{1}{2(n^2-2n-s-3t+tn+1)}\Big[(n+t-1)\log_2(n+t-1)+2s(2n+t-4)\log_2(2n+t-4)\\ & & +(n-2s-2t-1)(2n+t-3)\log_2(2n+t-3)\Big]+t(3n+t-7)\log_2(3n+t-7)\\ & & +t(2n+t-5)\log_2(2n+t-5)+\log_2(n^2-2n-s-3t+tn+1). \end{eqnarray*} This completes the proof.

Theorem 4. The marginal entropy of the lollipop graph \(C_{n,g}\) is given by the following formula,

• (i) If \(g\) is odd, then \begin{eqnarray*} I_D(C_{n,g})& = & -2-\log_23-\frac{12}{4n^3+5g^3-6ng^2-12g^2+12ng-10n+7g}\\ & & \times\Big[\sum_{i=1}^{n-g+1}\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g-1)\big]\\ & & \times\log_2\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g-1)\big]\\ & & +2\sum_{i=n-g+2}^{n-\frac{g-1}{2}}\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g-1)\big]\\ & & \times\log_2\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g-1)\big]\Big]\\ & & +\log_2\big[4n^3+5g^3-6ng^2-12g^2+12ng-10n+7g\big]. \end{eqnarray*}
• (ii) If \(g\) is even, then \begin{eqnarray*} I_D(C_{n,g})& = & -2-\log_23-\frac{12}{4n^3+5g^3-6ng^2-12g^2+12ng-4n+4g}\\ & & \times\Big[\sum_{i=1}^{n-g+1}\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g)\big]\\ & & \times\log_2\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g)\big]\\ & & +2\sum_{i=n-g+2}^{n-\frac{g}{2}}\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g)\big]\\ & & \times\log_2\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g)\big]\\ & & +\frac{1}{4}(2n^2+g^2-2ng+2n-2g)\log_2[\frac{1}{4}(2n^2+g^2-2ng+2n-2g)]\Big]\\ & & +\log_2\big[4n^3+5g^3-6ng^2-12g^2+12ng-4n+4g\big]. \end{eqnarray*}

Proof.

• (i) If \(g\) is odd, then we obtain \(D(v_i)\) according to the following \(A_1\) to \(A_3\).
  • (\(A_1\)) \(1\leq i\leq n-g+1\). Then \begin{eqnarray*} D(v_i) & = & \sum_{j=1}^{i-1}(i-j)+\sum_{j=i+1}^{n-g+1}(j-i)+2\sum_{j=n-g+2}^{\frac{2n-g+1}{2}}(j-i)\\ & = & \frac{i(i-1)}{2}+\frac{(n-g-i+2)(n-g-i+1)}{2}+(2n-\frac{3}{2}g-2i+\frac{5}{2})(\frac{g-1}{2})\\ & = & i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g-1). \end{eqnarray*}
  • (\(A_2\)) \(n-g+2\leq i\leq n-\frac{g-1}{2}\). Then \begin{eqnarray*} D(v_i) & = & 2\sum_{j=1}^{\frac{g-1}{2}}j+\sum_{j=1}^{n-g}(i-j)\\ \nonumber & = & (\frac{g+1}{2})(\frac{g-1}{2})+\frac{(2i-n+g-1)(n-g)}{2}\\ \nonumber & = & (n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g-1). \end{eqnarray*}
  • (\(A_3\)) \(n-\frac{g-3}{2}\leq i\leq n\), \(D(v_i)=D(v_{2n-g-i+2})\), and in this case \(n-g+2\leq 2n-g-i+2\leq n-\frac{g-1}{2}\).

    In summary, we have

    \begin{eqnarray*} \sum_{v\in V(C_{n,g})}D(v) & = & A_1+A_2+A_3\\ & = & \sum_{i=1}^{n-g+1}\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g-1)\big]\\ & & +2\sum_{i=n-g+2}^{n-\frac{g-1}{2}}\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g-1)\big]\\ & = & \frac{1}{12}(4n^3+5g^3-6ng^2-12g^2+12ng-10n+7g). \end{eqnarray*} Therefore, we have \begin{eqnarray*} I_D(C_{n,g})& = & -2-\log_23-\frac{12}{4n^3+5g^3-6ng^2-12g^2+12ng-10n+7g}\\ & & \times\Big[\sum_{i=1}^{n-g+1}\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g-1)\big]\\ & & \times\log_2\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g-1)\big]\\ & & +2\sum_{i=n-g+2}^{n-\frac{g-1}{2}}\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g-1)\big]\\ & & \times\log_2\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g-1)\big]\Big]\\ & & +\log_2\big[4n^3+5g^3-6ng^2-12g^2+12ng-10n+7g\big]. \end{eqnarray*}
• (ii) If \(g\) is even, then we obtain \(D(v_i)\) according to the following \(B_1\) to \(B_4\).
  • (\(B_1\)) \(1\leq i\leq n-g+1\). Then \begin{eqnarray*} D(v_i) & = & \sum_{j=1}^{i-1}(i-j)+\sum_{j=i+1}^{n-g+1}(j-i)+2\sum_{j=n-g+2}^{\frac{2n-g}{2}}(j-i)+(n-\frac{g}{2}+1-i ) \end{eqnarray*} \begin{eqnarray*} & = & \frac{i(i-1)}{2}+\frac{(n-g-i+2)(n-g-i+1)}{2}\\ & & +(2n-\frac{3}{2}g-2i+2)(\frac{g}{2}-1)+(n-\frac{g}{2}+1-i )\\ & = & i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g). \end{eqnarray*}
  • (\(B_2\)) \(n-g+2\leq i\leq n-\frac{g}{2}\). Then \begin{eqnarray*} D(v_i) & = & 2\sum_{j=1}^{\frac{g}{2}-1}j+\frac{g}{2}+\sum_{j=1}^{n-g}(i-j)\\ & = & \frac{g}{2}(\frac{g}{2}-1)+\frac{g}{2}+\frac{(2i-n+g-2)(n-g)}{2}\\ & = & (n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g). \end{eqnarray*}
  • (\(B_3\)) \(i=n-\frac{g}{2}+1\). Then \begin{eqnarray*} D(v_i) & = & 2\sum_{j=1}^{\frac{g}{2}-1}j+\frac{g}{2}+\sum_{j=1}^{n-g}(i-j)\\ & = & \frac{g}{2}(\frac{g}{2}-1)+\frac{g}{2}+\frac{(2i-n+g-2)(n-g)}{2}\\ & = & \frac{1}{4}(2n^2+g^2-2ng+2n-2g). \end{eqnarray*}
  • (\(B_4\)) \(n-\frac{g}{2}+2\leq i\leq n\), \(D(v_i)=D(v_{2n-g-i+2})\), and in this case \(n-g+2\leq 2n-g-i+2\leq n-\frac{g}{2}\).

    In summary, we have

    \begin{eqnarray*} \sum_{v\in V(C_{n,g})}D(v) & = & B_1+B_2+B_3+B_4\\ & = & \sum_{i=1}^{n-g+1}\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g)\big]\end{eqnarray*}\begin{eqnarray*} & & +2\sum_{i=n-g+2}^{n-\frac{g}{2}}\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g)\big]+\frac{1}{4}(2n^2+g^2-2ng+2n-2g)\\ &= & \frac{1}{12}(4n^3+5g^3-6ng^2-12g^2+12ng-4n+4g). \end{eqnarray*} Therefore, we have \begin{eqnarray*} I_D(C_{n,g})& = & -2-\log_23-\frac{12}{4n^3+5g^3-6ng^2-12g^2+12ng-4n+4g}\\ & & \times\Big[\sum_{i=1}^{n-g+1}\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g)\big]\\ & & \times\log_2\big[i^2-(n+1)i+\frac{1}{4}(2n^2-g^2+2n+2g)\big]\\ & & +2\sum_{i=n-g+2}^{n-\frac{g}{2}}\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g)\big]\\ & & \times\log_2\big[(n-g)i+\frac{1}{4}(-2n^2-g^2+4ng-2n+2g)\big]\\ & & +\frac{1}{4}(2n^2+g^2-2ng+2n-2g)\log_2[\frac{1}{4}(2n^2+g^2-2ng+2n-2g)]\Big]\\ & & +\log_2\big[4n^3+5g^3-6ng^2-12g^2+12ng-4n+4g\big]. \end{eqnarray*}
  This completes the proof.

Theorem 5. Let \(G\) be the \(n\)-vertex clique-chain graph \(G_d(a_1,a_2,\ldots,a_d,a_{d+1})\). Then the marginal entropy of \(G\) is given by the following formula \[ I_D(G) = -\frac{\sum_{k=1}^{d+1}a_k\Big[\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)\log_2\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)\Big]} {\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ka_i+\sum_{k=1}^{d+1}{a_k}^2+n} +\log_2\Big(\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ka_i+\sum_{k=1}^{d+1}{a_k}^2+n\Big). \]

Proof. Denote the set of all vertices in clique \(K_{a_k}\) by \(V_k\), then \(V(G)=\bigcup_{k=1}^{d+1}V_k\). For \(u\in V_k\) (\(1\leq k\leq d+1\)), \[D(u)=a_k-1+\sum_{i=1}^{k-1}(k-i)a_i+\sum_{i=k+1}^{d+1}(i-k)a_i=\sum_{i=1}^{d+1}|i-k|a_i+a_k-1.\] Then, we have \[\sum_{u\in V(G)}D(u)=\sum_{k=1}^{d+1}a_k\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)=\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ka_i+\sum_{k=1}^{d+1}{a_k}^2+\sum_{k=1}^{d+1}a_k\] and \[\sum_{u\in V(G)}D(u)\log_2D(u)=\sum_{k=1}^{d+1}a_k\Big[\big(\sum_{i=1}^{d+1}|i-k|+a_k-1\big)\log_2\big(\sum_{i=1}^{d+1}|i-k|+a_k-1\big)\Big].\] Therefore, recall that \(\sum_{k=1}^{d+1}a_k=n\), we have \begin{eqnarray*} I_D(G) &=& -\frac{1}{\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ka_i+\sum_{k=1}^{d+1}{a_k}^2+\sum_{k=1}^{d+1}a_k} \sum_{k=1}^{d+1}a_k\Big[\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)\log_2\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)\Big]\\ & & +\log_2\Big(\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ia_k+\sum_{k=1}^{d+1}{a_k}^2+\sum_{k=1}^{d+1}a_k\Big)\\ &=& -\frac{1}{\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ka_i+\sum_{k=1}^{d+1}{a_k}^2+n} \sum_{k=1}^{d+1}a_k\Big[\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)\log_2\big(\sum_{i=1}^{d+1}|i-k|a_i+a_k-1\big)\Big]\end{eqnarray*}\begin{eqnarray*} & & +\log_2\Big(\sum_{k=1}^{d+1}\sum_{i=1}^{d+1}|i-k|a_ka_i+\sum_{k=1}^{d+1}{a_k}^2+n\Big). \end{eqnarray*} This completes the proof.

In the following, we provide the calculation formulas of marginal entropy under two kinds of graph operations, Cartesian product and join. For convenience, in the following discussion we let \(n\), \(n_i\) equals to \(|V(G)|\), \(|V(G_i)|\) and let \(m\), \(m_i\) equals to \(|E(G)|\), \(|E(G_i)|\) with \(i\in\{1,2\}\), respectively. Similarly, we can omit the subscript \(G\) when it does not cause ambiguity, such as \(d(u,v)=d_G(u,v)\), \(d_1(u,v)=d_{G_1}(u,v)\), \(d_2(u,v)=d_{G_2}(u,v)\), \(D_1(u)=D_{G_1}(u)\), \(V_1=V(G_1)\), \(d_1(u)=d_{G_1}(u)\) etc.

Theorem 6. Let \(G_1\) and \(G_2\) be simple connected graphs and \(G=G_1\square G_2\). Then the marginal entropy of \(G\) is given by the following formula \[ I_D(G) = 1-\frac{\sum_{u_1\in V_1}\sum_{v_1\in V_2}\Big[n_2D_1(u_1)+n_1D_2(v_1)\Big]\log_{2}{\Big[n_2D_1(u_1)+n_1D_2(v_1)\Big]}}{2n_2^2W(G_1)+2n_1^2W(G_2)} + \log_{2}\Big[{n_2^2W(G_1)+n_1^2W(G_2)}\Big]. \]

Proof. By Definition 1 and Lemma 1, for \(u=(u_1,v_1)\in V(G)=V_1\times V_2\), the total distance of \(u\) is computed in the following \begin{eqnarray*} D(u) & = & \sum_{v=(u_2,v_2)\in V(G)}d(u,v)\\ & = & \sum_{u_2\in V_1}\sum_{v_2\in V_2}\Big[d_1(u_1,u_2)+d_2(v_1,v_2)\Big]\\ & = & |V_2|\sum_{u_2\in V_1}d_1(u_1,u_2)+|V_1|\sum_{v_2\in V_2}d_2(v_1,v_2)\\ & = & n_2D_1(u_1)+n_1D_2(v_1). \end{eqnarray*} By definition of marginal entropy, \(I_D(G)\) can be computed as \begin{eqnarray*} I_D(G) &=&-\frac{1}{\sum_{u\in V(G)}{D(u)}}\sum_{u\in V(G)}{D(u)}\log_{2}{D(u)}+\log_{2}{\sum_{u\in V(G)}{D(u)}} \\ &=& -\frac{\sum_{u_1\in V_1}\sum_{v_1\in V_2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)\log_{2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)}{\sum_{u_1\in V_1}\sum_{v_1\in V_2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)}\\ & & +\log_{2}\sum_{u_1\in V_1}\sum_{v_1\in V_2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)\\ &=& -\frac{\sum_{u_1\in V_1}\sum_{v_1\in V_2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)\log_{2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)}{n_2^2\sum_{u_1\in V_1}D_1(u_1)+n_1^2\sum_{v_1\in V_2}D_2(v_1)}\\ & & +\log_{2}\Big(n_2^2\sum_{u_1\in V_1}D_1(u_1)+n_1^2\sum_{v_1\in V_2}D_2(v_1)\Big)\\ &=& 1-\frac{\sum_{u_1\in V_1}\sum_{v_1\in V_2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)\log_{2}\big(n_2D_1(u_1)+n_1D_2(v_1)\big)}{2n_2^2W(G_1)+n_1^2W(G_2)}\\ & & +\log_{2}\Big(n_2^2W(G_1)+n_1^2W(G_2)\Big). \end{eqnarray*} This completes the proof.

Theorem 7. Let \(G_1\) and \(G_2\) be simple graphs (not necessarily connected) and \(G=G_1\vee G_2\). Then the marginal entropy of \(G\) is given by the following formula \begin{eqnarray*} I_D(G)&=& 1-\frac{1}{2\big(n_1^2+n_2^2+n_1n_2-n_2-n_2-m_2-m_2\big)}\Big[\sum_{u\in V_1}{\big(2n_1+n_2-d_1(u)-2\big)\log_{2}\big(2n_1+n_2-d_1(u)-2\big)}\\ \nonumber & & +\sum_{u\in V_2}{\big(2n_2+n_1-d_2(u)-2\big)\log_{2}\big(2n_2+n_1-d_2(u)-2\big)}\Big]+\log_{2}{\Big[n_1^2+n_2^2+n_1n_2-n_2-n_2-m_2-m_2\Big]}. \end{eqnarray*}

Proof. By Definition 2, for \(u\in V(G)=V_1\cup V_2\), we have

• \(D(u)=d_1(u)+|V_2|+2\big(|V_1|-d_1(u)-1\big)=2n_1+n_2-d_1(u)-2\) for \(u\in V_1\),
• \(D(u)=d_2(u)+|V_1|+2\big(|V_2|-d_2(u)-1\big)=2n_2+n_1-d_2(u)-2\) for \(u\in V_2\).

By definition of marginal entropy, \(I_D(G)\) can be computed as \begin{eqnarray*} I_D(G) &=& -\frac{1}{\sum_{u\in V(G)}{D(u)}}\sum_{u\in V(G)}{D(u)}\log_{2}{D(u)}+\log_{2}{\sum_{u\in V(G)}{D(u)}} \\ &=& -\frac{1}{\sum_{u\in V_1}{D(u)}+\sum_{u\in V_2}{D(u)}}\Big[\sum_{u\in V_1}{D(u)}\log_{2}{D(u)}+\sum_{u\in V_2}{D(u)}\log_{2}{D(u)}\Big]\\ & & +\log_{2}{\Big[\sum_{u\in V_1}{D(u)}+\sum_{u\in V_2}{D(u)}\Big]}\\ &=& -\frac{1}{\sum_{u\in V_1}{\big(2n_1+n_2-d_1(u)-2\big)}+\sum_{u\in V_2}{\big(2n_2+n_1-d_2(u)-2}\big)}\\ & & \times\Big[\sum_{u\in V_1}{\big(2n_1+n_2-d_1(u)-2\big)\log_{2}\big(2n_1+n_2-d_1(u)-2\big)}\\ & & +\sum_{u\in V_2}{\big(2n_2+n_1-d_2(u)-2\big)\log_{2}\big(2n_2+n_1-d_2(u)-2\big)}\Big]\\ & & +\log_{2}{\Big[\sum_{u\in V_1}{\big(2n_1+n_2-d_1(u)-2\big)}+\sum_{u\in V_2}{\big(2n_2+n_1-d_2(u)-2}\big)\Big]}\\ &=& -\frac{1}{n_1(2n_1+n_2-2)-\sum_{u\in V_1}{d_1(u)}+n_2(2n_2+n_1-2)-\sum_{u\in V_2}{d_2(u)}}\\ & & \times\Big[\sum_{u\in V_1}{\big(2n_1+n_2-d_1(u)-2\big)\log_{2}\big(2n_1+n_2-d_1(u)-2\big)}\\ & & +\sum_{u\in V_2}{\big(2n_2+n_1-d_2(u)-2\big)\log_{2}\big(2n_2+n_1-d_2(u)-2\big)}\Big]\\ & & +\log_{2}{\Big[n_1(2n_1+n_2-2)-\sum_{u\in V_1}{d_1(u)}+n_2(2n_2+n_1-2)-\sum_{u\in V_2}{d_2(u)}\Big]}\\ &=& 1-\frac{1}{2\big(n_1^2+n_2^2+n_1n_2-n_2-n_2-m_2-m_2\big)}\\ & & \times\Big[\sum_{u\in V_1}{\big(2n_1+n_2-d_1(u)-2\big)\log_{2}\big(2n_1+n_2-d_1(u)-2\big)}\\ & & +\sum_{u\in V_2}{\big(2n_2+n_1-d_2(u)-2\big)\log_{2}\big(2n_2+n_1-d_2(u)-2\big)}\Big]\\ & & +\log_{2}{\Big[n_1^2+n_2^2+n_1n_2-n_2-n_2-m_2-m_2\Big]}. \end{eqnarray*} This completes the proof.

4. Summary and discussions

In this paper, the marginal entropies of the complete bipartite graphs, complete multipartite graphs, firefly graphs, lollipop graphs, clique-chain graphs, Cartesian product and join of two graphs are obtained. For some other specific types of graphs, the existing results can be useful. For example, applying Cartesian product operation to \(P_m\) and \(P_n\), \(P_m\) and \(C_n\), \(C_m\) and \(C_n\) we can get grid graph, cylinder graph and torus graph with order \(mn\), respectively. In addition, Sahin obtained the marginal entropy for paths and cycles [15], so the formulas for above three special types of graphs can be done if readers are interested. And we note that \(K_{a,b}=\overline{K_a}\vee\overline{K_b}\). Since the join of any two graphs must be connected, one can also get Theorem 1 by Theorem 7. Similarly, \(K_{a_1,a_2,\ldots,a_k}=\overline{K_{a_1}}+\ldots+\overline{K_{a_k}}\), one can also study the multiple operations of graphs.

Acknowledgments

The authors are grateful to the anonymous referee for careful reading and valuable comments which result in an improvement of the original manuscript. This work was supported by the Natural Science Foundation of Qinghai Province (No. 2021-ZJ-703).

Author Contributions All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.