On the uniqueness of the Laplacian spectra of coalescence of complete graphs

1. Introduction

This study explores whether graphs are determined by their spectrum following [1] and [2]. The paper focuses on coalescence of complete graphs and their Laplacian spectra. A coalescence refers to the process of amalgamating vertices of two graphs [3]. These graphs are useful in management research as boards of directors can be regarded as complete graphs (all directors are related) [4,5,6,7]. Powerful directors called `hyper-agents` link two or more boards through their joint membership, creating board interlocks. These interlocked boards resemble coalescence of complete graphs. The spectra derived from such graphs have been analyzed empirically [4, 8]. These graphs tend to be large; hence, methods developed for complex networks have been applied [9]. Any empirical approach has to assume that mappings from the topology to the spectral domain and vice versa are one-to-one correspondences. Hence, it is implicitly assumed that these graphs are determined by their spectrum. However, it is not know whether coalescence of complete graphs are determined by their Laplacian spectrum. In fact, [10] shows that disjoint unions of complete graphs are only determined by their Laplacian spectrum if one excludes graphs with isolated vertices.

This study addresses two research questions: first, how does the number of vertices in the vertex cutset alter the spectrum; second, is a coalescence of complete graphs determined by its Laplacian spectrum? Both questions extend prior research by [10] on disjoint unions of complete graphs and are based on the methods reviewed in [1] and [2]. To derive Laplacian spectra, an approach using equitable partitions is used [11].

This study investigates three types of graphs formed by amalgamating vertices of disjoint unions of complete graphs. \S\ref{S1_1} defines the three types using coalescence and cones. A C1 graph refers to a vertex coalescence of two complete graphs, while a C2 graph is a cone over a disjoint union of \(k\) complete graphs. To analyze an increase in the size of the vertex cutset, C3 graphs emerge from C1 graphs by increasing the number of universal vertices. The majority of papers has focused on adjacency matrices of coalescence [12,13]. Yet, Laplacian eigenvalues are arguably more important [8]. In particular, the second smallest eigenvalue called the algebraic connectivity has been extensively studied [14].

Graphs resulting from a coalescence have been analyzed in spectral graph theory, e.g. in the context of unicyclic graphs, which refer to a cycle or a cycle with attached trees [13]. Further applications include lollipop graphs, i.e. the coalescence of a cycle and a path with pendant vertex as distinguished vertex [12], and dumbbell graphs, i.e. two disjoint cycles and a path joining them [15]. Coalescence of graphs also emerge from graph operations such as a join of two graphs [16].

There are many related concepts such as glued graphs [17, 18]. The definition of glued graphs does not permit trivial clones, which consist of a single vertex; however, C2 graphs defined in Definition4 can be regarded as a glued graph. To add to the confusion, the term glue graphs has been used – but it is unrelated [19]. Chains of cliques defined in [9], where neighboring complete graphs are fully interconnected are a special case of graphs where all vertices are `hyper-agents`. A C1 graph can be regarded as a block graphs as defined by [20,21]. However, C3 graphs are not block graphs as \(\mathbb{B}_1 \cap \mathbb{B}_2=1\) or \(0\) but not \(l>1\). Some findings might generalize to block graphs [20,21], which might be the subject of future research.

Simulations show that for \(n \rightarrow \infty\) graphs are almost certainly determined by their spectra [22]. However, [1] contends that – except if \(n< 5\) – it is difficult to prove that a graph is determined by its spectrum. Showing that a graph G is determined by its Laplacian spectrum involves to prove that any cospectral mate is isomorphic to G. As outlined in [1,2], there are three approaches: complete enumeration of all graphs (useful for small \(n\)), structural properties fixed by the spectrum, and the algorithm developed by [23,24,25]. This study follows the second approach.

The first research question analyzes how the spectrum changes if the number of vertices in the vertex cutset increases, while maintaining the same number of vertices. This matters in applications, e.g. one can ask whether the spectrum identifies if a director takes another directorship, which creates a so-called board interlock between two or more companies [6,7]. Section 3 derives several novel results for three types of coalescence of complete graphs (C1, C2, C3) with varying size of the vertex cutset. Theorem 4, 5 and 6 show that all Laplacian eigenvalues are integers; hence, coalescence of complete graphs are Laplacian integral graphs [26]. Most importantly, the second smallest Laplacian eigenvalue determines the minimum number of vertices in the vertex cutset, i.e. the vertex connectivity is equal to the algebraic connectivity. This finding is not a surprise as coalescence of complete graphs are equivalent to the construction based on the join operation developed by [27].

The second research question explores whether coalescence of complete graphs are determined by their Laplacian spectra. Corollary 2 and 3 based on [10] and [2], offer initial results for C1 and C2 graphs but impose restrictions. To remove these restrictions, Lemmas 5, 6 and 7 are derived, implying Theorem 7 stating that C1 graphs are determined by their Laplacian spectrum. Using induction and the spectrum derived in Section 3 leads to a generalization of Corollary 3 for C2 graphs. Theorem 9 establishes that C3 graphs are determined by their Laplacian spectra.

Section 2 briefly highlights important definitions and prior findings used in proofs. Section 3 and Section 4 focus on the first and second research question, respectively. Section 5 concludes.

2. Preliminaries

2.1. Cones and coalescence

Unless stated otherwise, a graph \(G\) refers to a simple graph with vertex set \(V(G)\) and edge set \(E(G)\). The number of vertices is \(n\), and the number of edges is \(e\). This study explores three types of graphs formed by amalgamating vertices of disjoint unions of complete graphs. To define these graphs, it is useful to introduce cones, cut vertices and vertex cutsets.

Definition 1.[28] A cone is the graph obtained from \(G\) by adding a universal vertex. The universal vertex is adjacent to all vertices of \(G\).

Definition 2.[29] A cut vertex of a graph \(G\) is any vertex that when removed increases the number of connected components of \(G\). Hence, if \(G\) has \(r\) cut vertices, then \(0 \leq r \leq n-2\).

Definition 3.[30] A vertex cutset of a graph \(G\) is a set of vertices whose deletion increases the number of connected components of \(G\). Hence, if the number of vertices in the vertex cutset is \(l\), then \(0 \leq l \leq n-2\).

The three types of graphs can be defined using cones over a disjoint union of complete graphs, where the number of universal vertices is equal to the number of vertices in the vertex cutset by construction and Definition 3. For instance, Figure 1 illustrates the construction of the first type (C1), where a universal vertex is added to a disjoint union of two complete graphs of size \(m_1-1\) and \(m_2-1\), i.e. a cone over the disjoint union of \(K_{m_1-1}\) and \(K_{m_2-1}\).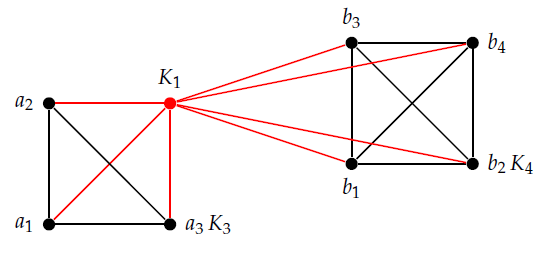

Cones are useful in showing that graphs are determined by their spectrum (e.g. Lemma 2). However, research on spectra of graphs often refers to alternative graph operations, where multigraphs \(G^*\) emerge from operations on a set of graphs, say \(\{G_1, G_2,\cdot\cdot\cdot \}\), and their spectra can be expressed in terms of spectra from \(\{G_1, G_2,\cdot\cdot\cdot \}\) [31]. To apply results derived in this stand of literature, it is useful to define the coalescence of two graphs.

Definition 4.[3] Any graph with a cut vertex, say \(w\), can be regarded as the coalescence \(G \circ H\) of the two graphs \(G\) and \(H\) obtained from the disjoint union of \(G\) and \(H\) by identifying a vertex \(u\) in \(G\) with a vertex \(v\) in \(H\).

It is important to observe that \(|V(G \circ H)|=|V(G-u)|+|V(H-v)|+1\). Using Definition 4, the cone over the disjoint union of \(K_{m_1-1}\) and \(K_{m_2-1}\) shown in Figure 1 can be regarded as a coalescence of \(K_{m_1}\) and \(K_{m_2}\). The operation described in Definition 4 is also called amalgamating vertex \(u\) and \(v\) [31] or overlapping vertices [32]. There are many related concepts such as glued graphs [17,18]. The definition of glued graphs, however, does not permit trivial clones, which consist of a single vertex. The literature has developed many alternative notations, e.g. [28] would denote a cone over a graph \(G\) with one universal vertex as \(\Delta_1(G)\). This study adopts the notation developed by [3]. A disjoint union of two graphs \(G_1\) and \(G_2\) is denoted \(G_1 \: \dot{\cup} \: G_2\), which avoids any confusion with unions of groups. The join of two disjoint graphs \(G_1\) and \(G_2\) refers to \(G_1 \bigtriangledown G_2\), where each vertex of \(G_1\) is connected to each vertex of \(G_2\). In line with Definition 1, a cone over \(G_1\) can be written as \(K_1 \bigtriangledown G_1\), where \(K_1\) is an isolated vertex, which becomes a universal vertex adjacent to all vertices of \(G_1\). A double cone over \(G_1\) refers to \(K_2 \bigtriangledown G_1=K_1 \bigtriangledown (K_1 \bigtriangledown G_1)\). Moreover, a coalescence of complete graphs and a cone over a disjoint union of complete graphs are equivalent, i.e. \(K_{m_1} \circ K_{m_2}=K_1 \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1})\). Using Definitions 1, 2 and 4 with the notation adopted from [3], the three types of graphs are defined. One could argue whether C2 graphs can be regarded as coalescence of complete graphs as Definition 4 refers to two graphs; hence, Definition 5 uses cones.

Definition 5. The three types of graphs obtained from amalgamating vertices of disjoint unions of complete graphs are defined as follows:

(C1) \(K_1 \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1})\), i.e. a cone over the disjoint union of two complete graphs of size \(m_1-1\) and \(m_2-1\) with \(m_1 \leq m_2\).

(C2) \(K_1 \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1} \: \dot{\cup} \:\cdot\cdot\cdot \: \dot{\cup} \: K_{m_k-1})\) with \(k>2\), i.e. a cone over the disjoint union of \(k\) complete graphs of size \(m_1-1, m_2-1,\cdot\cdot\cdot, m_k-1\) with \(m_1 \leq m_2 \leq\cdot\cdot\cdot \leq m_k\).

(C3) \(K_l \bigtriangledown (K_{s_1} \: \dot{\cup} \: K_{s_2})\) with \(2 \leq l \leq n-2\), i.e. an l-cone over the disjoint union of two complete graphs of size \(s_1\) and \(s_2\).

Based on Definition 5, Figure 1 represents a C1 graph. C2 graphs are obtained by adding cliques to Figure 1 maintaining a single cut vertex. Figure 2 shows a C3 graph, which is constructed from the C1 graph in Figure 1 by adding three edges to one of the vertices of the larger clique. Hence, there are two universal vertices and there are two vertices in the vertex cutset. By Definition 5, the graph in Figure 2 can be regarded as the double cone over the disjoint union of \(K_3\) and \(K_3\).

Based on Definition 5, the number of vertices is related to the size of cliques as follows \(n=\sum_{j=1}^k m_j-k+1\) for C1 and C2 graphs. Except stated otherwise, this study adopts two conventions without loss of generality. First, in the case of C3 graphs, the number of vertices \(n\) remains unchanged when the number of vertices in the vertex cutset \(l\) increases, which requires an adjustment of the size of the two cliques \(s_1\) and \(s_2\). Therefore, Section 3 refines the definition of C3 graphs to maintain \(n\). This ensures that comparing spectra for different values of \(l\) is meaningful as the dimension of the Laplacian matrix remains constant. Second, the size of cliques is ordered so that \(m_1 \leq m_2 \leq\cdot\cdot\cdot m_k\) in the case of C1 and C2 graphs.

2.2. Laplacian spectra and structural properties

The adjacency matrix refers to \({\mathbf A}\), the diagonal matrix of vertex degrees \(d_i\) for \(i=1, 2,\cdot\cdot\cdot, n\) is \({\mathbf D}\), and the Laplacian matrix is \({\mathbf L}={\mathbf D}-{\mathbf A}\) as in [33]. As shown in [1, Lemma 1], the Laplacian spectrum determines \(\text{tr}({\mathbf L}^j)\), which fixes several structural properties captured in Lemma 1. Note that \(\text{tr}\) is the trace of the matrix. To highlight that a matrix refers to a particular graph, the notation, e.g. \({\mathbf L}(G)\), is adopted; however, if the graph is clear from the context \((G)\) is dropped. Lemma 1 combines [34, Lemma 14.4.3] in \((i)\) to \((vi)\) and [33, Lemma 2.2] in \((vii)\).

Lemma 1. The following structural properties of the graph \(G\) can be deduced from the Laplacian spectrum, where \(t\) is the number of triangles.

1. The number of vertices.
2. The number of edges.
3. Whether \(G\) is regular.
4. Whether \(G\) is regular with any fixed girth.
5. The number of components.
6. The number of spanning trees.
7. \(\sum_{i=1}^n d_i^2\).
8. \(\sum_{i=1}^n d_i^3-6t\).

Definition 5 uses cones to describe the three types of graphs motivated by Lemma 2, which can be applied to derive Corollary 2 and 3 in Section 4.

Lemma 2. [2, Proposition 4] Let \(G\) be a disconnected graph that is determined by its Laplacian spectrum. Then the cone over \(G\) is also determined by its Laplacian spectrum.

Results for the disjoint union of two or more complete graphs are derived by [10], which are essential for analyzing C1 and C2 graphs. Adjusting the notation used by [10] in line with [3], Lemma 3 and 4 can be stated, where \(Sp_{\mathbf L}\) refers to the Laplacian spectrum.

Lemma 3.[2, Theorem 3.10.] The graph \(K_{s_1} \: \dot{\cup} \: K_{s_2}\) with \(s_1< \frac{3}{5}s_2\) is determined by its Laplacian spectrum.

Lemma 4.[2,Theorem 2.3.] If the Laplacian spectrum of \(H\) is \(Sp_{\mathbf L}=\{0^{(k)}, s_1^{(s_1-1)}, s_2^{(s_2-1)},\cdot\cdot\cdot, s_k^{(s_k-1)}\}\) with \(s_i \in \mathbb{N} \setminus \{0, 1\}\) then \(H\) is a disjoint union of complete graphs of order \(s_1,\cdot\cdot\cdot, s_k\).

The condition \(s_i \in \mathbb{N} \setminus \{0, 1\}\) for \(i=1, 2,\cdot\cdot\cdot, k\) in Lemma 4 does not permit isolated vertices. Hence, Lemma 4 states that the disjoint union of complete graphs without isolated vertex denoted \(H\) is determined by its Laplacian spectrum in the family of graphs without isolated vertex. The restriction to graphs without isolated vertices is important as e.g. \(K_{10} \: \dot{\cup} \: K_{6}\) is cospectral to \(L(K_6) \: \dot{\cup} \: K_{1}\), where \(L(K_6)\) is the line graph of \(K_6\) [10]. Lemma 1 states that the Laplacian spectrum determines the number of spanning trees of a graph \(G\) denoted \(\tau(G)\). Kirchoff’s Matrix-Tree Theorem links the Laplacian matrix and the number of spanning trees as follows.

Theorem 1.[35] The number of spanning trees in \(G\) is the absolute number of any cofactor of the Laplacian matrix of \(G\).

A cofactor of \({\mathbf L}(G)\) is the determinant of the Laplacian matrix after removing an arbitrary column and row. For complete graphs, the number of spanning trees can be calculated using Theorem 2, which is often referred to as Cayley’s Theorem derived by [36]. The original paper did not use the term spanning tree; however, recent papers restate the result and provide several proof, e.g. [37].

Theorem 2.[36] The number of spanning trees of a complete graph with \(n\) vertices is \(\tau(K_n)=n^{n-2}\).

The following result reported by [32] can be derived by applying Theorem \ref{P2a} or using a double counting proof similar to [37]. [32] use yet another approach based on Laplacian energy.

Corollary 1. [32,Corollary 5] The number of spanning trees of the coalescence \(K_m \circ K_n\) is \(\tau(K_m \circ K_n)=\tau(K_m)\tau(K_n)=m^{m-1}n^{n-2}\).

To discuss the Laplacian spectra derived in Section 3, it is useful to define algebraic connectivity and vertex connectivity.

Definition 6.[38] The second smallest Laplacian eigenvalue is the algebraic connectivity of a graph \(G\) denoted \(a(G)\).

Definition 7.[30] The vertex connectivity \(\kappa_0(G)\) of the connected graph \(G\) is the minimum number of vertices in a vertex cutset.

The following theorem helps to understand why Laplacian spectra reveal the vertex connectivity of coalescence of complete graphs (C1 and C3) and the cone over the disjoint union of \(k\) complete graphs (C2) as shown in Section 3.

Theorem 3.[27, Theorem 2.1] Let \(G\) be a connected, non-complete graph with \(n\) vertices. Then \(a(G)=\kappa_0(G)\) if and only if \(G\) can be written as the join \(G_1 \bigtriangledown G_2\), where \(G_1\) is a disconnected graph on \(n-\kappa_0(G)\) vertices and \(G_2\) is a graph on \(\kappa_0(G)\) vertices and \(a(G_2) \geq 2\kappa_0(G)-n\).

2.3. Equitable partitions and spectra

In spectral graph theory, most results for the coalescence of graphs focus on the adjacency matrix [39] using a deletion-contraction approach [40]. The Laplacian spectrum is usually explored in the context of graph energy, and some results for complete graphs are derived by [32] using chromatic polynomials [41]. Among other findings, [32] determine the Laplacian energy of the vertex and edge coalescence of two complete graphs. The former graph is equal to C1 graphs by Definition 5 and the latter refers to a C2 graph with two vertices in the vertex cutset, i.e. \(l=2\). To obtain the Laplacian energy of a vertex coalescence in [32, Theorem 4]and an edge coalescence in [32, Theorem 12], the Laplacian spectrum of C1 graphs is derived and the characteristic polynomial of C2 graphs with \(l=2\). Theorem 4 is consistent with [32, Theorem 4], and Theorem 5 generalizes [32, Theorem 12] for all C2 graphs. The methodology, however, is different. In contrast to [32], this study uses equitable partitions following a similar approach as in a recent paper by [11], where characteristic polynomials of so-called pineapple graphs are derived. Pineapple graphs refer to a coalescence of a complete graph with a star \(K_{1,q}\) at the vertex of degree \(q\). As the adjacency matrix of a pineapple graph contains one clique, the structure is similar to the three types of graphs based on Definition 5.

3. Deriving the Laplacian spectra

Section 3.1 derives the Laplacian spectra of C1 graphs, and Section 3.2 shows how the spectrum changes due to increasing the number of vertices in the vertex cutset while maintaining the same number of vertices, a construction illustrated in Figure 2. Section 3.3 determines Laplacian spectra of C2 graphs.

3.1. The spectrum of C1 graphs

Generalizing the method illustrated by an example in Section 2.3 to any \(m_1\) and \(m_2\) yields Theorem 4.

Theorem 4. The Laplacian spectrum of C1 graphs is \(\text{Sp}_{\mathbf L}=\{0, 1, m_1^{(m_1-2)}, m_2^{(m_2-2)},n\}\).

Proof. The Laplacian of C1 graphs, which can be regarded as \(K_{m_1} \circ K_{m_2}\) or \(K_1 \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1})\) with \(m_1 \leq m_2\), can be written as follows, where \({\mathbf L_i}=m_i{\mathbf I}-{\mathbf J}\) with \(i=1, 2\). \begin{equation}\tag{1} {\mathbf L}= \begin{bmatrix} m_1+m_2-2 & -{\mathbf 1^T} & -{\mathbf 1^T} \\ -{\mathbf 1} & {\mathbf L_2} & {\mathbf O} \\ -{\mathbf 1} & {\mathbf O} & {\mathbf L_1} \\ \end{bmatrix} \label{E3_10} \end{equation} Vertices are ordered by degree such that \(\deg(v_1) \geq \deg(v_2) \geq\cdot\cdot\cdot \geq \deg(v_n)\). Applying the equitable partition \(\pi=(\{v_1\}, \{v_2,\cdot\cdot\cdot, v_{m_2}\}, \{v_{m_2+1},\cdot\cdot\cdot, v_{m_1+m_2-1}\})\) yields the \(3 \times 3\) quotient matrix \({\mathbf Q}_\pi\). \begin{equation} \tag{2}{\mathbf Q}_\pi= \begin{bmatrix} m_1+m_2-2 & -(m_2-1) & -(m_1-1) \\ -1 & 1 & 0 \\ -1 & 0 & 1 \\ \end{bmatrix} \label{E3_11} \end{equation} From \eqref{E3_10}, \(\text{rank}(m_i{\mathbf I}-{\mathbf L})=n-(m_i-2)\) with \(i=1, 2\); hence, \({\mathbf L}\) has eigenvalues \(m_1\) with multiplicity \(n-n+(m_1-2)=m_1-2\) and \(m_2\) with multiplicity \(m_2-2\). The characteristic polynomial for the Laplacian can be written as follows. \begin{equation}\tag{3} C_{\mathbf L}(x)=(x-m_1)^{m_1-2}(x-m_2)^{m_2-2}C_{{\mathbf Q}_\pi}(x) \label{E3_12} \end{equation} The characteristic polynomial with respect to the quotient matrix follows from \eqref{E3_11} taking \(\det(x{\mathbf I}-{\mathbf Q}_\pi)\). Note that the number of vertices is \(n=m_1+m_2-1\). \begin{aligned} C_{{\mathbf Q}_\pi}(x)&= \begin{vmatrix} x-(m_1+m_2-2) & m_2-1 & m_1-1 \\ 1 & x-1 & 0 \\ 1 & 0 & x-1 \\ \end{vmatrix} \label{E3_13} \\ &=(x-(m_1+m_2-2))(x-1)^2-(m_2-1)(x-1)-(m_1-1)(x-1) \\ &=(x-1)(x^2-(m_1+m_2-1)x) \\ &=(x-1)(x-n)x \end{aligned} Hence, the characteristic polynomial for the Laplacian can be written as follows. \begin{equation}\tag{4} C_{\mathbf L}(x)=(x-m_1)^{m_1-2}(x-m_2)^{m_2-2}(x-1)(x-n)x \label{E3_14} \end{equation} Equation \eqref{E3_14} yields the Laplacian spectrum \(\text{Sp}_{\mathbf L}=\{0, 1, m_1^{(m_1-2)}, m_2^{(m_2-2)},n\}\).

Theorem 4 confirms the results shown in [32, Theorem 4]used to derive the Laplacian energy of a vertex coalescence of two complete graphs.

3.2. Increasing the number of vertices in the vertex cutset

Starting from a C1 graph and its Laplacian spectrum derived in Theorem 4, the questions arise how the Laplacian spectrum changes due to increasing the number of vertices in the vertex cutset and whether the Laplacian spectrum reveals the number of vertices in the vertex cutset. These two questions are relevant in the context of social networks. The following discussion leads to a refined definition of C3 graphs compared to Definition 5. There are three different approaches to increase the number of vertices in the vertex cutset starting with a C1 graph, leading to a C3 graph. First, using the notation in [32] the coalescence \(K_{m_1} \underset{^w}\circ K_{m_2}\) refers to the C1 graph, where \(w\) is the cut vertex. Increasing the number of vertices in the vertex cutset can be achieved by amalgamating two or more vertices, e.g. \(K_{m_1} \underset{^{uv}}\circ K_{m_2}\) as in [32], which refers to the edge \(uv\), i.e. two vertices are amalgamated. Using this construction, it is obvious that the number of vertices declines with an increase in the number of vertices in the vertex cutset denoted \(l\) as \(n=m_1+m_2-l\). Second, starting with a C1 graph additional vertices in the cutset can be added as universal vertices using double, triple and higher-order cones such that \(K_l \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1})\) with \(m_1 \leq m_2\). This construction increases the number of vertices as \(l\) increases as \(n=m_1+m_2-2+l\). Third, the second approach is used but without changing the number of vertices. By convention and without loss of generality the number of vertices is maintained at \(n=(m_1-1-l_1)+(m_2-l_2)+l=m_1+m_2-1\) where \(l=l_1+l_2\) and again by convention \(l_1=0\) and \(l_2=1\) if \(l=1\). Hence, any additional vertex in the vertex cutset reduces the number of vertices in \(K_{m_1-1-l_1}\) or \(K_{m_2-l_2}\). Maintaining the number of vertices makes a comparison of spectra, to demonstrate the increase in the size of the vertex cutset, more relevant as the dimension of the Laplacian matrix remains constant. Obviously, changing the number of vertices alters the spectrum as the dimension of the Laplacian matrix changes. This case is less interesting mathematically and also less relevant in the context of board memberships as the size of boards rarely changes. Consequently, the third construction is used to derive Theorem 5.

Theorem 5. Starting with a C1 graph and increasing the number of vertices in the vertex cutset \(l\), while maintaining the number of vertices \(n=m_1+m_2-1\), generates the Laplacian spectrum. \begin{aligned} \text{Sp}_{\mathbf L}&=\{0, l, m_1^{(m_1-l_1-2)}, m_2^{(m_2-l_2-1)},n^{(l)}\}, \quad l=l_1+l_2 \end{aligned} The number of vertices in the vertex cutset \(l\) is the second smallest eigenvalue and has multiplicity one. The multiplicity of the eigenvalue \(n\) is equal to the number of vertices in the vertex cutset.

Proof. Starting with a C1 graph, the number of vertices in the vertex cutset increases to \(l>1\) and the number of vertices in \(K_{m_1-1-l_1}\) and \(K_{m_2-l_2}\) is adjusted so that \(l=l_1+l_2\) ensuring that \(n=m_1+m_2-1\), where \({\mathbf L_1}=m_1{\mathbf I}-{\mathbf J}\) and \({\mathbf L_2}=m_2{\mathbf I}-{\mathbf J}\) with appropriate dimensions. Matrix \({\mathbf H}\) has dimension \(l \times l\) capturing the \(l\) vertices in the vertex cutset, where \({\mathbf H}=(m_1+m_2-1){\mathbf I}-{\mathbf J}\). \begin{equation} \tag{5}{\mathbf L}= \begin{bmatrix} {\mathbf H} & -{\mathbf J} & -{\mathbf J} \\ -{\mathbf J} & {\mathbf L_2} & {\mathbf O} \\ -{\mathbf J} & {\mathbf O} & {\mathbf L_1} \\ \end{bmatrix} \label{E3_15} \end{equation} Vertices are ordered by degree such that \(\deg(v_1) \geq \deg(v_2) \geq\cdot\cdot\cdot \geq \deg(v_n)\). The equitable partition \(\pi\) has three cells, where all vertices in matrix \({\mathbf H}\) are in cell one, all vertices in matrix \({\mathbf L_2}\) are in cell two, and cell three contains all vertices in matrix \({\mathbf L_1}\). Note that increasing the number of vertices in the vertex cutset does not alter the degree in each cell of the partition, only the number of vertices in each degree class changes. The equitable partition yields the \(3 \times 3\) quotient matrix \({\mathbf Q}_\pi\), where each element is the row sum of the respective block of \({\mathbf L}\). \begin{equation}\tag{6} {\mathbf Q}_\pi= \begin{bmatrix} m_1+m_1-1-l & -(m_2-l_2) & -(m_1-1-l_1) \\ -l & l & 0 \\ -l & 0 & l \\ \end{bmatrix} \label{E3_16} \end{equation} From \eqref{E3_15}, \(\text{rank}(m_1{\mathbf I}-{\mathbf L})=n-(m_1-l_1-2)\); hence, \({\mathbf L}\) has eigenvalue \(m_1\) with multiplicity \(n-n+(m_1-l_1-2)=m_1-l_1-2\). Then \(\text{rank}(m_2{\mathbf I}-{\mathbf L})=n-(m_2-l_2-1)\), implying that \({\mathbf L}\) has eigenvalue \(m_2\) with multiplicity \(n-n+(m_2-l_2-1)=m_2-l_2-1\). Finally, \(\text{rank}((m_1+m_2-1){\mathbf I}-{\mathbf L})=n-(l-1)\); thus, \({\mathbf L}\) has eigenvalue \(m_1+m_2-1\) with multiplicity \(l-1\). Using these results, the characteristic polynomial of the Laplacian can be written as follows. \begin{equation}\tag{7} C_{\mathbf L}(x)=(x-m_1)^{m_1-l_1-2}(x-m_2)^{m_2-l_2-1}(x-n)^{l-1}C_{{\mathbf Q}_\pi}(x) \label{E3_17} \end{equation} The characteristic polynomial with respect to the quotient matrix follows from \eqref{E3_16} taking \(\det(x{\mathbf I}-{\mathbf Q}_\pi)\). \begin{aligned} C_{{\mathbf Q}_\pi}(x)&= \begin{vmatrix} x-(m_1+m_2-1-l) & m_2-l_2 & m_1-1-l_1 \\ l & x-l & 0 \\ l & 0 & x-l \\ \end{vmatrix} \label{E3_18} \nonumber \\ &=(x-(m_1+m_2-1-l))(x-l)^2-l(m_2-l_2)(x-l) \nonumber \\ &-l(m_1-1-l_1)(x-l) \nonumber \\ &=(x-l)(x^2-(m_1+m_2-1)x) \nonumber \\ &=(x-l)(x-n)x \end{aligned} Hence, the characteristic polynomial of the Laplacian can be written as follows. \begin{equation} C_{\mathbf L}(x)=(x-m_1)^{m_1-l_1-2}(x-m_2)^{m_2-l_2-1}(x-n)^{l-1}(x-l)(x-n)x \label{E3_19} \nonumber \\ =(x-m_1)^{m_1-l_1-2}(x-m_2)^{m_2-l_2-1}(x-n)^{l}(x-l)x \end{equation} Equation (8) yields the Laplacian spectrum. \begin{equation}\tag{8} \text{Sp}_{\mathbf L}=\{0, l, m_1^{(m_1-l_1-2)}, m_2^{(m_2-l_2-1)},n^{(l)}\} \label{E3_20} \end{equation}

Theorem 5 generalizes [32, Theorem 12] for all \(l>2\) and identifies all eigenvalues. In contrast, [32, Theorem 12] provides the characteristic polynomial. Only for the special case if \(m_1=m_2\), [32] calculates all eigenvalues.

Setting \(l=1\), \(l_1=0\) and \(l_2=1\) yields the Laplacian spectrum \(\text{Sp}_{\mathbf L}=\{0, 1, m_1^{(m_1-2)},m_2^{(m_2-2)}, n\}\) consistent with Theorem 4. Furthermore, setting \(l=0\) the Laplacian spectrum derived in Theorem 5 replicates the Laplacian spectrum of a disjoint union of two complete graphs adjusting for differences in notation in [10]. Basically, this study uses the convention \(K_{m_1-1-l_1}\) and \(K_{m_2-l_2}\), i.e. \(l=0\) implies \(l_1=l_2=0\). Therefore, \(K_{m_1-1} \: \dot{\cup} \: K_{m_2}\) compared to the notation \(K_{k_1} \: \dot{\cup} \: K_{k_2}\) used in [10], i.e. the number of vertices \(k_1=m_1+1\), which corrects the multiplicity of the eigenvalue \(m_1\).

Theorem 5 shows that the Laplacian spectrum reveals the number of vertices in the vertex cutset \(l\). By Definition 5 and 7, C3 graphs refer to an l-cone over the disjoint union of two complete graphs; hence, by construction there is only one vertex cutset, implying that \(l=\kappa_0(C3)\). Furthermore by Definition 6, \(l=\kappa_0(C3)=a(C3)\); thus, C3 graphs exhibit equal vertex and algebraic connectivity.

This finding is not surprising as the construction of C3 graphs fulfills the necessary and sufficient conditions of Theorem 3 guaranteeing that graphs exhibit equal vertex and algebraic connectivity. This can be seen by setting \(G_1=K_{s_1} \: \dot{\cup} \: K_{s_2}\), which is a disconnected graph on \(n-l\) vertices, and \(G_2=K_l\). Note the condition \(a(G_2) \geq 2\kappa_0(G)-n\) holds as \(G_2=K_l\) and the Laplacian spectrum of a complete graph is \(Sp_{\mathbf L}=\{0, l^{(l-1)}\}\); thus, \(a(K_l)=l\). By Definition 5, \(\kappa_0(C3)=l\) implying \(a(K_l)=l \geq 2l-n \Leftrightarrow l \leq n\). This holds as \(l \leq n-2\) by Definition 3.

3.3. Laplacian spectra of C2 graphs

Extending the proof of Theorem 4, which focuses on \(k=2\), yields the following result for C2 graphs.

Theorem 6. The Laplacian spectrum of C2 graphs with \(k>2\) is \(\text{Sp}_{\mathbf L}=\{0, 1^{(k-1)}, m_1^{(m_1-2)}, m_2^{(m_2-2)},\cdot\cdot\cdot , m_k^{(m_k-2)},n\}\).

Proof. The proof of Theorem 6 is a generalization of the proof of Theorem 4, which is more detailed. Equation \eqref{E3_21} shows the Laplacian of C2 graphs. \begin{equation}\tag{9} {\mathbf L}= \begin{bmatrix} \sum_{i=1}^km_i-k & -{\mathbf 1^T} &\cdot\cdot\cdot & -{\mathbf 1^T} \\ -{\mathbf 1} & {\mathbf L_k} &\cdot\cdot\cdot & {\mathbf O} \\ \vdots & \vdots & \vdots & \vdots \\ -{\mathbf 1} & {\mathbf O} &\cdot\cdot\cdot & {\mathbf L_1} \\ \end{bmatrix} \label{E3_21} \end{equation} Using the equitable partition \(\pi\) of the blocks of \({\mathbf L}\) in \eqref{E3_21} yields the \((k+1) \times (k+1)\) quotient matrix \({\mathbf Q}_\pi\). \begin{equation}\tag{10} {\mathbf Q}_\pi= \begin{bmatrix} \sum_{i=1}^km_i-k & -(m_k-1) &\cdot\cdot\cdot & -(m_1-1) \\ -1 & 1 &\cdot\cdot\cdot & 0 \\ \vdots & \vdots & \vdots & \vdots \\ -1 & 0 &\cdot\cdot\cdot & 1 \\ \end{bmatrix} \label{E3_22} \end{equation} From \eqref{E3_21}, \(\text{rank}(m_i{\mathbf I}-{\mathbf L})=n-(m_i-2)\); hence, \({\mathbf L}\) has eigenvalues \(m_i\) with multiplicity \(m_i-2\) for \(i=1,\cdot\cdot\cdot, k\). The characteristic polynomial with respect to the quotient matrix follows from \eqref{E3_22} taking \(\det(x{\mathbf I}-{\mathbf Q}_\pi)\). Note that the number of vertices is \(n=\sum_{i=1}^km_i-k+1\). \begin{aligned} C_{{\mathbf Q}_\pi}(x)&= \begin{vmatrix} x-\left(\sum_{i=1}^km_i-k\right) & m_k-1 &\cdot\cdot\cdot & m_1-1 \\ 1 & x-1 &\cdot\cdot\cdot & 0 \\ \vdots & \vdots & \vdots & \vdots \\ 1 & 0 &\cdot\cdot\cdot & x-1 \\ \end{vmatrix} \label{E3_23} \nonumber \\ &=\left(x-\left(\sum_{i=1}^km_i-k\right)\right)(x-1)^k-(m_k-1)(x-1)^{k-1} \nonumber \\ &-\cdot\cdot\cdot -(m_k-1)(x-1)^{k-1} \nonumber \\ &=(x-1)^{k-1}(x-n)x \end{aligned} Based on the analysis of the rank of \(m_i{\mathbf I}-{\mathbf L}\), \eqref{E3_24} shows the characteristic polynomial for the Laplacian, concluding the proof. \begin{equation}\tag{11} C_{\mathbf L}(x)=(x-m_1)^{m_1-2}\cdot\cdot\cdot\cdot \cdot (x-m_k)^{m_k-2}(x-1)^{k-1}(x-n)x \label{E3_24} \end{equation}

4. Uniqueness of Laplacian spectra

Section 4 explores whether coalescence of complete graphs are determined by their Laplacian spectra focusing on C1, C2 and C3 graphs based on Definition 5.

4.1. C1 graphs are determined by their Laplacian spectra

Applying Lemma 2 and 3 together with Definition 5 shows that C1 graphs are determined by their Laplacian spectra under certain conditions.

Corollary 2. A cone over the disjoint union of two complete graphs of size \(m_1-1\) and \(m_2-1\), respectively, is determined by its Laplacian spectrum if \(m_1< \frac{3}{5}m_2+\frac{2}{5}\).

Proof. Based on Definition 5, C1 graphs refer to a cone over the disjoint union of two complete graphs of size \(m_1-1\) and \(m_2-1\). Based on Lemma 3, the disjoint union of two complete graphs \(K_{s_1} \: \dot{\cup} \: K_{s_2}\) is determined by its Laplacian spectrum if \(s_1< \frac{3}{5}s_2\). Thus applying Lemma 2 and the condition \(m_1-1< \frac{3}{5}(m_2-1) \Leftrightarrow m_1< \frac{3}{5}m_2+\frac{2}{5}\) Corollary 2 follows.

Corollary 2 imposes the condition \(m_1< \frac{3}{5}m_2+\frac{2}{5}\); hence, the question arises whether this condition can be relaxed. The answer is yes as demonstrated by Theorem 7. To establish Theorem 7, this section proves Lemma 5, 6 and 7.

Lemma 5. Let \(G\) and \(G’\) be C1 graphs that are cospectral with respect to the Laplacian matrix. Then \(G\) and \(G’\) are isomorphic.

Proof. As \(G\) and \(G’\) are C1 graph, it follows from Definition 5, \(G=K_1 \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1})\) with \(m_1 \leq m_2\) and \(G’=K_1 \bigtriangledown (K_{s_1-1} \: \dot{\cup} \: K_{s_2-1})\) with \(s_1 \leq s_2\). Structural properties of the graph \(G\) fixed by the Laplacian spectrum include the number of vertices and edges as outlined in Lemma 1. Inspecting Figure 1, it is apparent that the Laplacian of \(G\) has the structure shown in \eqref{E1}, where vertices are ordered by degree. The universal vertex labeled \(K_1\) in Figure 1 is adjacent to the \(m_1-1\) vertices in \(K_{m_1-1}\) and the \(m_2-1\) vertices in \(K_{m_2-1}\), resulting in degree \(m_1+m_2-2\). Accordingly, the \(m_1-1\) vertices in \(K_{m_1-1}\) have degree \(m_1-1\) as they are adjacent to the universal vertex labeled \(K_1\) and the other \(m_1-2\) vertices in \(K_{m_1-1}\). Similarly, the \(m_2-1\) vertices in \(K_{m_2-1}\) have degree \(m_2-1\). \begin{equation}\tag{12} {\mathbf L}(G)=\underbrace{\begin{bmatrix} m_1+m_2-2 & 0 & 0 & \dots & 0 \\ 0 & m_2-1 & 0 & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & 0 & m_1-1 & 0 \\ 0 & 0 & 0 & \dots & m_1-1 \end{bmatrix}}_{m_1+m_2-1}-{\mathbf A}(G) \label{E1} \end{equation} The trace of the Laplacian follows from \eqref{E1}. Obviously, \(\text{tr}\:({\mathbf L}(G)^0)=m_1+m_2-1=n\), the number of vertices. The number of edges follows from \(\text{tr}\:({\mathbf L}(G))=\sum_{i=1}^n d_i=2e\) stated in Lemma 1. Considering \(\text{tr}\:({\mathbf L}(G))=\text{tr}\:({\mathbf D}(G))-\text{tr}\:({\mathbf A}(G))\), where \(\text{tr}\:({\mathbf A}(G))=0\) by definition, yields the following. \begin{aligned} \text{tr}\:({\mathbf L}(G))&=m_1+m_2-2+(m_2-1)^2+(m_1-1)^2 \label{E2} \nonumber \\ &=m_2(m_2-1)+m_1(m_1-1) \nonumber \\ &=m_1^2+m_2^2-m_1-m_2 \end{aligned} The second line above shows that the number of edges of \(G\) is equal to the number of edges of the disjoint union of two complete graphs \(K_{m_1} \: \dot{\cup} \: K_{m_2}\) – but the coalescence \(G\) has one less vertex as two vertices are amalgamated into one in line with Definition 4. As \(G\) and \(G’\) are cospectral \(C1\) graphs, \(\text{tr}\:({\mathbf L}(G)^j)=\text{tr}\:({\mathbf L}(G’)^j)\) where \(j\) is a positive integer shown in \cite[Lemma 1]{Haemers2003} implying that \(G\) and \(G’\) exhibit the same structural properties fixed by the Laplacian spectrum. Thus, \(G\) and \(G’\) have the same number of vertices implying \(n=m_1+m_2-1=s_1+s_2-1\) so that \(m_2=n+1-m_1\) and \(s_2=n+1-s_1\). Then using (4.1) and \(\text{tr}\:({\mathbf L}(G))=\text{tr}\:({\mathbf L}(G’))\) implies the following. \begin{aligned} m_1^2+(n+1-m_1)^2-m_1-(n+1-m_1)&=s_1^2+(n+1-s_1)^2-s_1-(n+1-s_1) \label{E3} \nonumber \\ 2m_1^2+2m_1+n^2-n-2&=2s_1^2+2s_1+n^2-n-2 \nonumber \\ m_1(m_1+1)&=s_1(s_1+1) \end{aligned} Hence, it follows that \(s_1=m_1\) and hence \(s_2=m_2\), implying that \(G\) and \(G’\) are isomorphic.

Lemma 6. Let \(G’\) be a graph with exactly one cut vertex. Then \(G’\) is cospectral to the C1 graph \(G\) if and only if \(G’\) is a C1 graph.

Proof. As the Laplacian spectrum fixes the number of spanning trees (see Lemma 1), the cospectral graph \(G’\) must have the same number of spanning trees. The C1 graph \(G\) refers to a coalescence of two complete graphs of size \(m_1\) and \(m_2\) with \(m_1 \leq m_2\). Applying Corollary 1 yields the number of spanning trees of graph \(G\) denoted \(\tau(G)\), where \(n=m_1+m_2-1\). \begin{aligned} \tau(G)&=\tau(K_{m_1})\tau(K_{m_2})=m_1^{m_1-2}m_2^{m_2-2} \label{E4} \nonumber \\ &=m_1^{m_1-2}(n+1-m_1)^{n-m_1-1} \end{aligned} Is it possible to achieve the same number of spanning trees by moving vertices between the two cliques connected by the universal vertex if the number of edges must be constant? To avoid redundant edges, one can only move vertices from the smaller clique (initially the clique \(K_{m_1}\)) denoted \(G_1’\) to the larger clique denoted \(G_2’\). Removing vertices and their edges from \(G_1’\) results in a smaller clique. Hence, \eqref{E5} states the number of spanning trees after removing \(v\) vertices. \begin{equation}\tag{13} \tau(G_1′-v)=(m_1-v)^{m_1-v-2} \label{E5} \end{equation} Moving the \(v\) vertices to the larger subgraph \(G_2’\) results in a complete graph with \(v\) additional vertices but edges need to be removed, where \(\Delta|E(G_2′)|\) denotes the change in the number of edges required. \begin{aligned} \Delta|E(G_2′)|&=\left[\left(\begin{array}{c} m_2+v \\ 2 \end{array}\right)-\left(\begin{array}{c} m_2 \\ 2 \end{array}\right)\right]-\left[\left(\begin{array}{c} m_1 \\ 2 \end{array}\right)-\left(\begin{array}{c} m_1-v \\ 2 \end{array}\right)\right] \label{E6} \nonumber \\ &=\frac{1}{2}\left[(v^2+2m_2v-v)-(2m_1v-v^2-v)\right] \nonumber \\ &=v^2+v(m_2-m_1)=v^2+v(n+1-2m_1) \end{aligned} By Theorem 2, the number of spanning trees in the complete graph with \(m_2+v\) vertices before adjusting the edges is \(\tau(G_2’+v)=(m_2+v)^{m_2+v-2}=(n+1-m_1+v)^{n-m_1+v-1}\). By symmetry, every edge of this complete graph is contained in \(b\) spanning trees determined as follows. Note that every spanning tree has \(n-m_1+v\) edges. \begin{aligned} (n-m_1+v)(n+1-m_1+v)^{n-m_1+v-1}&=b\left(\begin{array}{c} n+1-m_1+v \\ 2 \end{array}\right) \label{E7} \nonumber \\ (n-m_1+v)(n+1-m_1+v)^{n-m_1+v-1}&=\frac{1}{2}b(n+1-m_1+v)(n-m_1+v) \nonumber \\ b&=2(n+1-m_1+v)^{n-m_1+v-2} \end{aligned} Hence, the number of spanning trees in \(G_2’\) after adding \(v\) vertices and adjusting the number of edges yields the following. \begin{aligned} \tau(G_2’+v-e)&=(n+1-m_1+v)^{n-m_1+v-1} \label{E8} \nonumber \\ &-2(v^2+v(n+1-2m_1))(n+1-m_1+v)^{n-m_1+v-2} \nonumber \\ &=(n+1-m_1+v)^{n-m_1+v-2}\left[n+1-m_1-v(1+2v+2n-4m_1))\right] \end{aligned} Hence, the number of spanning trees of \(G’\) yields. \begin{aligned} \tau(G’)&=\tau(G_1′-v)\tau(G_2’+v-e) \label{E9} \nonumber \\ &=(m_1-v)^{m_1-v-2}(n+1-m_1+v)^{n-m_1+v-2}\nonumber \\ &\cdot \left[n+1-m_1-v(1+2v+2n-4m_1)\right] \end{aligned} Is there a positive integer \(v\) so that \(\tau(G’)=\tau(G)\)? \begin{aligned} m_1^{m_1-2}(n+1-m_1)^{n-m_1-1}&=(m_1-v)^{m_1-v-2}(n+1-m_1+v)^{n-m_1+v-2} \label{E10} \nonumber \\ &\cdot \left[n+1-m_1-v(1+2v+2n-4m_1)\right] \end{aligned} Equality only holds for \(v=0\); thus, \(G’\) must have two cliques, implying that \(G’\) is a C1 graph.

Lemma 7. If \(G’\) has more than one vertex in its vertex cutset(s) or more than one cut vertex then \(G’\) cannot be cospectral to the C1 graph \(G\).

Proof. Figure 3 illustrates an increase in the number of vertices in the vertex cutset. Without loss of generality, let \(G\) be the coalescence \(K_4 \circ K_4\), which is the smallest C1 graph with all options for edge removals. The graph \(G’\) with \(l=2\) is obtained from \(G\) by adding the edge \((26)\) (dashed red line). In this case, \(\{3, 6\}\) and \(\{2, 3\}\) are the two cutsets with two vertices in each. The number of edges needs to be reduced by one to ensure that \(G’\) and \(G\) have the same number of edges.

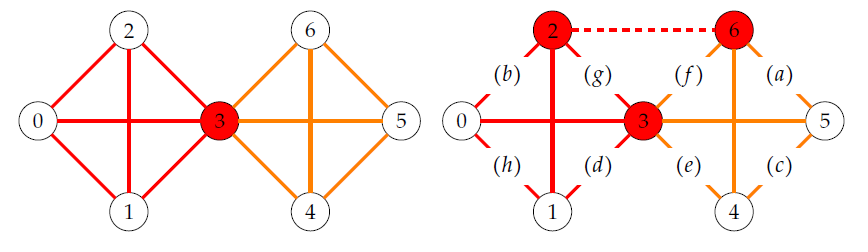
Before removing one edge, there are at most five valencies in \(G’\): one vertex with degree \(d_1=m_1+m_2-2\) (vertex \(3\) in Figure 3), one vertex with degree \(d_2=m_1\) (vertex \(2\)), one vertex with degree \(d_3=m_2\) (vertex \(6\)), \(m_1-2\) vertices with with degree \(d_4=m_1-1\) (vertices \(0\) and \(1\)), and \(m_2-2\) vertices with with degree \(d_5=m_2-1\) (vertices \(4\) and \(5\)). Hence, there are ten options to select two out of five valencies to remove one edge plus two options selecting two vertices with the same degree \(d_4\) or \(d_5\). Yet, four options are not permitted. First, by Definition 2, the edge connecting \(2\) and \(6\) (dashed red line) cannot be removed as \(2\) and \(6\) would not be vertices in the vertex cutsets. Second, there are no edges that can be removed between vertices that are not in the same clique or in one of the vertex cutsets (e.g. \(0\) and \(5\)). Third, there are no edges between the new vertex in the cutset \(6\) and vertices with degree \(d_4\). Fourth, there are no edges between the new vertex in the cutset \(2\) and vertices with degree \(d_5\). Therefore, eight options remain that lead to a different degree sequence labeled \((a)\) to \((h)\) in Figure 3.

Table 1 shows the degree sequences of these eight options and the conditions that have to hold to ensure that \(\sum_{i=1}^n d_i^2\) remains unchanged as required by Lemma 1 (see Cond 1 in Table 1). Options \((b)\) and \((h)\) can be excluded as the conditions \(m_1=m_2+1\) and \(m_1=m_2+2\) violate \(m_1 \leq m_2\). Lemma 1 also requires that \(G’\) must have the same \(\sum_{i=1}^n d_i^3-6t\) as the graph \(G\). Counting the number of triangles \(t\) in an irregular graph such as \(G’\) is difficult – but it is sufficient to state that \(t(G’)< t(G)\) as \(G\) has two cliques maximizing the number of triangles for a given number of edges. Hence, the inequality \(\sum_{i=1}^n d_i^3(G')< \sum_{i=1}^n d_i^3(G)\) must hold (see Cond 2 in Table 1).

Table 1. Degree sequences with additional vertices in cutset.

Option (a)		Option (b)		Option (c)		Option (g)
\(\#\)	\(d_i\)	\(\#\)	\(d_i\)	\(\#\)	\(d_i\)	\(\#\)	\(d_i\)
\(1\)	\(m_1+m_2-2\)	\(1\)	\(m_1+m_2-2\)	\(1\)	\(m_1+m_2-2\)	\(1\)	\(m_1+m_2-3\)
\(1\)	\(m_2-2\)	\(1\)	\(m_2\)	\(1\)	\(m_2\)	\(1\)	\(m_1-1\)
\(1\)	\(m_1\)	\(1\)	\(m_1-2\)	\(1\)	\(m_1\)	\(1\)	\(m_2\)
\(m_1-2\)	\(m_1-1\)	\(m_1-2\)	\(m_1-1\)	\(2\)	\(m_2-2\)	\(m_1-2\)	\(m_1-1\)
\(m_2-2\)	\(m_2-1\)	\(m_2-2\)	\(m_2-1\)	\(m_1-2\)	\(m_1-1\)	\(m_2-2\)	\(m_2-1\)
\(-\)	\(-\)	\(-\)	\(-\)	\(m_2-4\)	\(m_2-1\)	\(-\)	\(-\)
Cond 1: \(m_1=m_2-1\)		\(m_1=m_2+1\)		\(m_1=m_2-2\)		\(m_1=2\)
Cond 2: equal		\(-\)		larger		equal
Option (d)		Option (e)		Option (f)		Option (h)
\(\#\)	\(d_i\)	\(\#\)	\(d_i\)	\(\#\)	\(d_i\)	\(\#\)	\(d_i\)
\(1\)	\(m_1+m_2-3\)	\(1\)	\(m_1+m_2-3\)	\(1\)	\(m_1+m_2-3\)	\(1\)	\(m_1+m_2-2\)
\(1\)	\(m_1\)	\(1\)	\(m_2\)	\(1\)	\(m_1\)	\(1\)	\(m_1\)
\(1\)	\(m_1-2\)	\(1\)	\(m_1\)	\(m_2-1\)	\(m_2-1\)	\(1\)	\(m_2\)
\(1\)	\(m_2\)	\(1\)	\(m_2-2\)	\(m_1-2\)	\(m_1-1\)	\(2\)	\(m_1-2\)
\(m_1-3\)	\(m_1-1\)	\(m_1-2\)	\(m_1-1\)	\(-\)	\(-\)	\(m_1-4\)	\(m_1-1\)
\(m_2-2\)	\(m_2-1\)	\(m_2-3\)	\(m_2-1\)	\(-\)	\(-\)	\(m_2-2\)	\(m_2-1\)
Cond 1: \(m_1=3\)		\(m_2=3\)		\(m_2=2\)		\(m_1=m_2+2\)
Cond 2: \(m_2< 2\)		\(m_1< 2\)		equal		\(-\)

\end{table} Table 1 reports whether this inequality (Cond 2) is fulfilled substituting any conditions needed to ensure that the sum of squared degrees remains unchanged (Cond 1). For instance, in option \((a)\) \(\sum_{i=1}^n d_i^3(G’)=\sum_{i=1}^n d_i^3(G)\) for all values of \(m_1\) and \(m_2\) that fulfill Condition 1. Option \((d)\) is not possible as \(m_1 \leq m_2\) so that the two conditions cannot hold. Option \((e)\) is not possible as \(m_1=1\) is not permitted as without the cut vertex there are no vertices in one of the cliques. Finally, one could combine these eight options by adding and removing more than one edge. As shown in Table 1, however, \(\sum_{i=1}^n d_i^3(G’)< \sum_{i=1}^n d_i^3(G)\) is not fulfilled by any option. The Laplacian fixes \(\sum_{i=1}^n d_i\) and \(\sum_{i=1}^n d_i^2\), which can be regarded as holding the expected value and variance of degrees constant. Any change in the distribution of degrees that preserves the variance contributes to an increase in the skewness related to \(\sum_{i=1}^n d_i^3\). Hence, Lemma 7 follows.

Combining Lemmas 5, 6 and 7, the condition in Corollary 2 can be removed leading to Theorem 7.

Theorem 7. \(C1\) graphs are determined by their Laplacian spectrum.

Proof. Based on Lemma 7, a graph \(G’\) cospectral to the \(C1\) graph \(G\) can only have one cut vertex, which implies following Lemma 6 that \(G’\) is a \(C1\) graph. Finally, Lemma 5 guarantees that any \(C1\) graph cospectral to the \(C1\) graph \(G\) is isomorphic to \(G\). Therefore, any graph \(G’\) cospectral to the \(C1\) graph \(G\) is isomorphic to \(G\).

4.2. C2 graphs are determined by their Laplacian spectra

Combining prior results, Corollary 3 follows for C2 graphs.

Corollary 3. \(K_1 \bigtriangledown (K_{m_1-1} \: \dot{\cup} \: K_{m_2-1} \: \dot{\cup} \:\cdot\cdot\cdot \: \dot{\cup} \: K_{m_k-1})\) with \(k>2\), i.e. a cone over the disjoint union of \(k\) complete graphs of size \(m_1-1\), \(m_2-1\), \(\cdot\cdot\cdot\), \(m_k-1\) with \(m_1 \leq m_2 \leq\cdot\cdot\cdot m_k\) and \(m_i \in \mathbb{N} \setminus \{1, 2\}\) is determined by its Laplacian spectrum in the family of graphs without isolated vertex.

Proof. The graph C2 is a cone obtained from \(k\) disjoint complete graphs of size \(m_1-1, m_2-1,\cdot\cdot\cdot, m_k-1\). Based on Lemma 4, the disjoint union of \(k\) complete graphs is determined by its Laplacian spectrum in the family of graphs without isolated vertex, i.e. \(m_i \in \mathbb{N} \setminus \{1, 2\}\). Thus applying Lemma 2, Corollary 3 follows.

Corollary 3 is of limited use due to its restriction to the family of graphs without isolated vertex, which cannot be deduced from the spectrum [10]. For instance, \(K_{10} \: \dot{\cup} \: K_{6}\) is cospectral to \(L(K_6) \: \dot{\cup} \: K_{1}\), where \(L(K_6)\) is the line graph of \(K_6\) [10]. Therefore, all graphs with isolated vertices need to be excluded. A C2 graph cannot be cospectral to a graph with isolated vertices as the latter exhibits the eigenvalue \(0\) with multiplicity in excess of one. Yet the restrictive condition in Corollary 3 cannot be dropped based on this observation as it is possible that there exists another graph cospectral to a C2 graph, which is not isomorphic. Theorem 7 establishes that C1 graphs are determined by their Laplacian spectra. By Definition 5, C2 graphs are C1 graphs if one permits \(k=2\). Accordingly, the strategy is to use induction to generalize Theorem 7 for \(k>2\), implying that all C2 graphs are determined by their Laplacian spectra. However, \(k=3\) suggests two possibilities, a C2 graph, i.e. one universal vertex connecting \(k=3\) cliques of size \(m_1-1\), \(m_2-1\) and \(m_3-1\), or a graph with two cut vertices. From Theorem 5, it is apparent that the number of cut vertices would be revealed by the spectrum. Hence, induction on \(k\) should be able to establish that C2 graphs are determined by their Laplacian spectra for \(k>2\). To proceed, one could go through the same steps leading to Theorem 7 using induction, which is a time-consuming task. It is more elegant to apply Theorem 6, which derives the Laplacian spectrum of C2 graphs.

Theorem 8. C2 graphs are determined by their Laplacian spectra.

Proof. Based on Theorem 7, it is assumed that C2 graphs with \(k=q\) are determined by their Laplacian spectra. By Theorem 6, these graphs exhibit the Laplacian spectrum \(\left.\text{Sp}_{\mathbf L}\right|_{k=q}\)\(=\{0, 1^{(q-1)}, m_1^{(m_1-2)}, m_2^{(m_2-2)},\cdot\cdot\cdot , m_q^{(m_q-2)}, n\}\). By assumption, any graph that has the same spectrum must be isomorphic to the C2 graph with \(k=q\). By Theorem 6, the C2 graph with \(k=q+1\) has the spectrum \(\left.\text{Sp}_{\mathbf L}\right|_{k=q+1}\)\(=\{0, 1^{(q)}, m_1^{(m_1-2)}, m_2^{(m_2-2)},\cdot\cdot\cdot , m_q^{(m_q-2)}, m_{q+1}^{(m_{q+1}-2)}, n\}\). Note that \(m_{q+1}\) does not have to be less or equal to \(m_{q}\) as eigenvalues can be reordered. Therefore, increasing \(k\) from \(q\) to \(q+1\) changes the spectrum by adding the eigenvalues \(1\) and \(m_{q+1}\) with multiplicity \((m_{q+1}-2)\). The only possibility that the C2 graph with \(k=q+1\) is not determined by its Laplacian spectrum is to find a subgraph, say \(H\), that is connected to the C2 graph with \(k=q\) as the multiplicity of the zero eigenvalue is one and changes the spectrum as required. From the change in the spectrum, it follows that \(H\) is an end-block that is a clique.A block is connected to two neighboring blocks by two cut vertices, whereas an end-block is connected to one neighboring block by one cut vertex [42]. Therefore, \(H\) must be a clique with the same cut vertex as the other \(k=q\) cliques, concluding the proof.

4.3. C3 graphs are determined by their Laplacian spectra

Theorem 9. C3 graphs are determined by their Laplacian spectra.

Proof. Based on Theorem 7, if \(l=1\) C3 graphs are determined by their Laplacian spectrum as they resemble C1 graphs. Using induction on \(l\) assumes that C3 graphs with \(l=q\) are determined by their Laplacian spectrum. Increasing \(l\) to \(l’=q+1\) changes the Laplacian spectrum derived in Theorem 5, where two cases have to be considered \(l_1’=l_1\) and \(l_2’=l_2+1\) (CASE 1) or \(l_1’=l_1+1\) and \(l_2’=l_2\) (CASE 2). In both cases, the algebraic connectivity increases to \(a(G)=q+1\), and the eigenvalues are \(0\), \(q+1\), \(m_1\) and \(m_2\). Between the two cases, only multiplicities differ. A graph cospectral to a C3 graph with \(l’=q+1\) must contain two end-blocks (permitting a single vertex cutset of size \(l\)) that are cliques of size \(m_1\) and \(m_2\), implying that any cospectral mate is isomorphic to a C3 graph.

5. Conclusion

This study shows that a vertex-coalescence of two complete graphs (C1 graph) is determined by its Laplacian spectrum (see Theorem 7). Theorem 8 establishes that a cone over the disjoint union of more than two complete graphs (C2 graph) is determined by its Laplacian spectrum. Amalgamating more than one vertex of two complete graphs results in C3 graphs that are determined by their Laplacian spectra (see Theorem 9). These findings are novel.

Furthermore, Laplacian spectra of coalescence of complete graphs are derived starting with C1 graphs in Theorem 4 and C2 graphs in Theorem 6. The most interesting finding refers to \(l\) cones over a disjoint unions of two complete graphs (C3 graph). Theorem 5 highlights that the number of vertices in the vertex cutset \(l\) is one of the eigenvalues with multiplicity one. Moreover, the multiplicity of the eigenvalue \(n\), the number of vertices, is equal to the number of vertices in the vertex cutset. Accordingly, the Laplacian spectrum reveals the number of vertices in the vertex cutset in coalescence of complete graphs. These findings can be applied in the field of management research, where corporate networks formed through board membership are explored.

Acknowledgement

I would like to thank Nicole Snashall for her encouragement, comments and support. I also would like to thank Jozef Siran for his comments on amalgamations, which led to more thinking about defining my graphs. This project started with an application to social networks; however, it developed into a much more general study. I would like to dedicate this paper to the memory of Alto Zeitler (1945-2022), my mathematics teacher.

Author Contributions:

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

“The authors declare no conflict of interest.”