The forgotten index of complement graph operations and its applications of molecular graph

1. Introduction

Theory of chemical graphs is the branch of mathematical chemistry that applies theory of graphs to mathematical modeling of chemical phenomena. In chemical graph theory a molecular graph is a simple graph in which the vertices and edges represent atoms and chemical bonds between them. In this paper, \(G\) be a simple connected graph with vertex set \(V(G)\) and edge set \(E(G)\). The number of elements in \(V(G)\) and \(E(G)\) is represented as \(|V (G)|\) and \(|E(G)|\), respectively. For a vertex \(u \in V (G)\), the number of vertices adjacent to the vertex \(u\) is called the degree of \(u\), denoted by \(\delta_G (u)\). The complement of \(G\), denoted by \(\overline{G}\) , is a simple graph on the same set of vertices \(V(G)\) in which two vertices \(u\) and \(v\) are adjacent, i.e., connected by an edge \(uv\), if and only if they are not adjacent in \(G\). Hence, \(uv\in E(\overline {G})\), if and only if \(uv\notin E(G)\). Obviously \(E(G)\cup E(\overline {G})=E(K_n)\), and \(\overline {m} =|E(\overline{G})|=\binom n{2}-m\), the degree of a vertex \(u\) in \(\overline {G}\), is the number of edges incident to \(u\), denoted by \(\delta_{\overline {G}}(u)=n-1-\delta_{G}(u)\) [1]. The well-known Zagreb indices introduced in [2] are among the most important topological indices. The first and second Zagreb indices \(M _1\) and \(M _2\), respectively, are defined for a molecular graph G as: \[{M_1}(G) = \sum\limits_{v \in V(G)} {\delta _G}^{2}(v)=\sum\limits_{uv \in E(G)} [{\delta _G}(u) + {\delta _G}(v)], \quad \quad {M_2}(G) = \sum\limits_{uv \in E(G)} {{\delta _G}(u)\,{\delta _G}(v)}. \] The first and second Zagreb coindices have been introduced by Ashrafi et al., in 2010 [3], they are respectively defined as: \[{\overline{M}_1}(G) = \sum\limits_{uv \notin E(G)} [{\delta _G}(u) + {\delta _G}(v)], \quad \quad {\overline{M}_2}(G) = \sum\limits_{uv \notin E(G)} {{\delta _G}(u)\,{\delta _G}(v)}. \] Furtula and Gutman in 2015 introduced forgotten index (F-index) [4] which is defined as: \[F(G) = \sum\limits_{v \in V(G)} {{ {\delta _G}^3(v)} }= \sum\limits_{uv \in E(G)} {\left( {{\delta _G}^2(u)\, + {\delta _G}^2(v)} \right)}. \] De et al., in 2016 defined forgotten coindex (F-coindex)[5] which is defined as: \[\overline {F}(G) = \sum\limits_{uv \notin E(G)} {\left( {{\delta _G}^2(u)\, + {\delta _G}^2(v)} \right)}. \] Then, De et al., in 2016 [6] computed the forgotten index of join \(G_1+G_2\), tensor product \(G_1 \otimes G_2\), Cartesian product \(G_1\times G_2\), composition \(G_1\circ G_2\), strong product \(G_1\ast G_2\), disjunction \(G_1\vee G_2\) and symmetric difference \(G_1\oplus G_2\) of two graphs. Here we continue this line of research by exploring the behavior of the forgotten index under the same operations of complement graphs. The results are applied to molecular graph of nanotorus and titania nanotubes. In recent years, there has been considerable interest in general problems of determining topological indices and their operations [1,7,8,9].

2. Preliminaries

In this section we give some basic and preliminary concepts which we shall use later.

Lemma 1.[10,11] Let \(G_1\) and \(G_2\) be two connected graphs with \(|V (G_1 )|=n_1\), \(|V (G_2 )|=n_2\), \( |E (G_1 )|=m_1\), and \(|E (G_2 )|=m_2\). Then

• 1. \(|V (G_1 \times G_2 )|= |V (G_1\vee G_2 )|= |V (G_1 \circ G_2 )|= |V (G_1 \otimes G_2 )|= |V (G_1 \ast G_2 )|=|V (G_1 \oplus G_2 )|=n_1 n_2,\)

  \(|V (G_1+ G_2 )|= n_1+ n_2,\)

• 2. \(|E(G_1 \times G_2)| = m_1 n_2 + n_1 m_2,\)

  \(|E(G_1 \ast G_2 )|= m_1 n_2+n_1 m_2+2m_1 m_2,\)

  \( |E(G_1+G_2)| = m_1+m_2+n_1 n_2,\)

  \(|E(G_1 \circ G_2)| = m_1 {n_2}^2 +m_2 n_1,\)

  \(|E(G_1\vee G_2 )|=m_1 {n_2}^2 +m_2 {n_1}^2 – 2m_1 m_2,\)

  \( | E(G_1 \otimes G_2)| = 2m_1 m_2,\)

  \(|E(G_1 \oplus G_2)| = m_1 {n_2}^2 + m_2 {n_1}^2 – 4m_1 m_2.\)

Proposition 1. [12] Let \(G\) be a simple graph on \(n\) vertices and \(m\) edges. Then. \[ F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G).\]

3. Discussion and main results

In this section, we study the forgotten index of various complement graph binary operations such as join, tensor product, Cartesian product, composition, strong product, disjunction and symmetric difference of two simple connected graphs. We use the notation \(V( G_i)\) for the vertex set, \(E( G_i)\), \(E(\overline G_i)\) for the edge sets, \(n_i\) for the number of vertices and \(m_i\), \(\overline m_i\) for the number of edges of the graph \(G_i\), \(\overline G_i\) respectively. All graphs here offer are simple graphs.

Definition 1(Join). The join \(G_{1}+ G_{2}\) of two graphs \(G_{1}\) and \(G_{2}\) is a graph with vertex set \(V (G_{1}+G_{2} )=V(G_{1}) \cup V(G_{2})\) and edge set \(E(G_{1})\cup E(G_{1}) \cup \{{uv| u \in V(G_{1}), v\in V (G_{2})}\}\).

Theorem 1. The \(F-index\) of the complement of \(G_1+ G_2 \) is given by \begin{eqnarray*} F(\overline{G_1+ G_2}) &=&(n_1+n_2)(n_1+n_2 – 1)^3 – 6(m_1+m_2+n_1 n_2)(n_1+n_2- 1)^2 \\ &&+ 3(n_1+n_2- 1)[M_1 (G_1 )+M_1 (G_2 )+n_1 n_2^2+n_2 n_1^2+4m_1 n_2+4m_2 n_1]\\ && -[F(G_1 )+F( G_2 )+3n_2 M_1 (G_1 )+3n_1 M_1 (G_2 )+6n_2^2 m_1+6n_1^2 m_2+n_1 n_2^3+n_2 n_1^3]. \end{eqnarray*}

Proof. From Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G) \), and since \(M_1 (G_1+ G_2 )=M_1 (G_1 )+M_1 (G_2 )+n_1 n_2^2+n_2 n_1^2+4m_1 n_2+4m_2 n_1\), given in [10], \(F(G_1+ G_2 )=F(G_1 )+F( G_2 )+3n_2 M_1 (G_1 )+3n_1 M_1 (G_2 )+6n_2^2 m_1+6n_1^2 m_2+n_1 n_2^3+n_2 n_1^3\), given in [6]. and \( |E(G_1+ G_2 )|=m_1+m_2+n_1 n_2,\quad |V(G_1+ G_2)|=n_1+n_2\) given in Lemma 1. Then \begin{eqnarray*} F(\overline{G_1+ G_2}) &=&|V(G_1+ G_2)|(|V(G_1+ G_2)| – 1)^3 – 6|E(G_1+ G_2 )|(|V(G_1+ G_2)| – 1)^2 \\ && +3(|V(G_1+ G_2)| – 1)M_1(G_1+ G_2 ) – F(G_1+ G_2 )\\ &=&(n_1+n_2)(n_1+n_2 – 1)^3 – 6(m_1+m_2+n_1 n_2)(n_1+n_2- 1)^2 \\ && +3(n_1+n_2- 1)[M_1 (G_1 )+M_1 (G_2 )+n_1 n_2^2+n_2 n_1^2+4m_1 n_2+4m_2 n_1]\\ && -[F(G_1 )+F( G_2 )+3n_2 M_1 (G_1 )+3n_1 M_1 (G_2 )+6n_2^2 m_1+6n_1^2 m_2+n_1 n_2^3+n_2 n_1^3]. \end{eqnarray*}

Definition 2(Tensor product). The tensor product \(G_{1}\otimes G_{2}\) of two graphs \(G_{1}\) and \(G_{2}\) is the graph with vertex set \(V(G_{1})\times V(G_{2})\) and any two vertices \((u_{1},v_{1})\) and \((u_{2},v_{2})\) are adjacent if and only if \(u_{1}u_{2}\in E(G_1)\) and \(v_{1}v_{2}\in E(G_2)\).

Theorem 2. The \(F-index\) of the complement of \(G_1\otimes G_2 \) is given by \begin{eqnarray*} F(\overline{G_1\otimes G_2}) &=&n_1n_2(n_1n_2- 1)^3 – 12m_1 m_2(n_1n_2- 1)^2 + 3(n_1n_2- 1)M_1 (G_1 ) M_1 ( G_2 )- F(G_1 )F( G_2 ). \end{eqnarray*}

Proof. From Proposition 1 we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G) \), and since \(M_1 (G_1\otimes G_2 )=M_1 (G_1 ) M_1 ( G_2 )\) given in [13], \(F(G_1\otimes G_2 )=F(G_1 )F( G_2 )\) given in [6]. and \( |E(G_1\otimes G_2 )|=2m_1 m_2,\quad |V(G_1\otimes G_2)|=n_1n_2\) given in Lemma 2.1. Then. \begin{eqnarray*} F(\overline{G_1\otimes G_2}) &=&|V(G_1\otimes G_2)|(|V(G_1\otimes G_2)| – 1)^3 – 6|E(G_1\otimes G_2 )|(|V(G_1\otimes G_2)| – 1)^2 \\ && +3(|V(G_1\otimes G_2)| – 1)M_1(G_1\otimes G_2 ) – F(G_1\otimes G_2 )\\ &=&n_1n_2(n_1n_2- 1)^3 – 12m_1 m_2(n_1n_2- 1)^2 +3(n_1n_2- 1)M_1 (G_1 ) M_1 ( G_2 )- F(G_1 )F( G_2 ). \end{eqnarray*}

Definition 3(Cartesian product). The Cartesian product \(G_{1}\times G_{2}\), of two simple and connected graphs \(G_{1}\) and \(G_{2}\) has the vertex set\(V(G_{1}\times G_{2})=V(G_{1})\times V(G_{2})\) and \((a,x)(b,y)\) is an edge of \(G_{1}\times G_{2}\) if \(a = b\) and \(xy\in E(G_{2})\), or \(ab\in E(G_{1})\) and \(x = y\).

Theorem 3. The \(F-index\) of the complement of \(G_1\times G_2 \) is given by \begin{eqnarray*} F(\overline{G_1\times G_2}) &=&n_1n_2(n_1n_2- 1)^3 – 6(m_1 n_2 + n_1 m_2)(n_1n_2- 1)^2+ 3(n_1n_2- 1)[n_2 M_1 (G_1 )+n_1 M_1 (G_2 )+8m_1 m_2]\\ && -[n_2 F(G_1 )+n_1 F( G_2 )+6m_2 M_1 (G_1 )+6m_1 M_1 (G_2 )]. \end{eqnarray*}

Proof. From Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G) \), and since \(M_1 (G_1\times G_2 )=n_2 M_1 (G_1 )+n_1 M_1 (G_2 )+8m_1 m_2\), given in [14], \(F(G_1\times G_2 )=n_2 F(G_1 )+n_1 F( G_2 )+6m_2 M_1 (G_1 )+6m_1 M_1 (G_2 ),\) given in [6]. and \( |E(G_1\times G_2 )|=m_1 n_2 + n_1 m_2,\quad |V(G_1\times G_2)|=n_1n_2\) given in Lemma 1. Then \begin{eqnarray*} F(\overline{G_1\times G_2}) &=&|V(G_1\ast G_2)|(|V(G_1\ast G_2)| – 1)^3 – 6|E(G_1\ast G_2 )|(|V(G_1\ast G_2)| – 1)^2 \\ && +3(|V(G_1\ast G_2)| – 1)M_1(G_1\ast G_2 ) – F(G_1\ast G_2 )\\ &=&n_1n_2(n_1n_2- 1)^3 – 6(m_1 n_2 + n_1 m_2)(n_1n_2- 1)^2 \\ && +3(n_1n_2- 1)[n_2 M_1 (G_1 )+n_1 M_1 (G_2 )+8m_1 m_2]\\ && -[n_2 F(G_1 )+n_1 F( G_2 )+6m_2 M_1 (G_1 )+6m_1 M_1 (G_2 )]. \end{eqnarray*}

Definition 4(Composition). The composition \(G_{1}\circ G_{2}\), of two simple and connected graphs \(G_{1}\) and \(G_{2}\) with disjoint vertex sets \( V(G_{1})\) and \( V(G_{2})\) and edge sets \( E(G_{1})\) and \( E(G_{2})\) is the graph with vertex set \(V(G_{1})\times V(G_{2})\) and \(u = (u_{1},v_{1})\) is adjacent with \(v=(u_{2},v_{2})\) whenever (\(u_{1}\) is adjacent with \(u_{2}\)) or {\(u_{1}=u_{2}\) and \(v_{1}\) is adjacent with \(v_{2}\)}.

Theorem 4. The \(F-index\) of the complement of \(G_1\circ G_2 \) is given by \begin{eqnarray*} F(\overline{G_1\circ G_2}) &=&n_1n_2(n_1n_2- 1)^3 – 6(m_1 {n_2}^2 +m_2 n_1)(n_1n_2- 1)^2 \\ && +3(n_1n_2- 1)[n_2^3 M_1 (G_1 )+ n_1 M_1 (G_2 )+ 8n_2 m_2 m_1]\\ && -[n_2^4 F(G_1 )+n_1 F( G_2 )+6n_2^2 m_2 M_1 (G_1 )+6n_2 m_1 M_1 (G_2 )]. \end{eqnarray*}

Proof. From Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G) \), and since \(M_1 (G_1\circ G_2 )= n_2^3 M_1 (G_1 )+ n_1 M_1 (G_2 )+ 8n_2 m_2 m_1\), given in [14]. \(F(G_1 \circ G_2)=n_2^4 F(G_1 )+n_1 F( G_2 )+6n_2^2 m_2 M_1 (G_1 )+6n_2 m_1 M_1 (G_2 ),\) given in [6]. and \( |E(G_1\circ G_2 )|=m_1 {n_2}^2 +m_2 n_1,\quad |V(G_1\circ G_2)|=n_1n_2\) given in Lemma 1. Then \begin{eqnarray*} F(\overline{G_1\circ G_2}) &=&|V(G_1\circ G_2)|(|V(G_1\circ G_2)| – 1)^3 – 6|E(G_1\circ G_2 )|(|V(G_1\circ G_2)| – 1)^2 \\ && +3(|V(G_1\circ G_2)| – 1)M_1(G_1\circ G_2 ) – F(G_1\circ G_2 )\\ &=&n_1n_2(n_1n_2- 1)^3 – 6(m_1 {n_2}^2 +m_2 n_1)(n_1n_2- 1)^2 \\ && +3(n_1n_2- 1)[n_2^3 M_1 (G_1 )+ n_1 M_1 (G_2 )+ 8n_2 m_2 m_1]\\ && -[n_2^4 F(G_1 )+n_1 F( G_2 )+6n_2^2 m_2 M_1 (G_1 )+6n_2 m_1 M_1 (G_2 )]. \end{eqnarray*}

Definition 5 (Strong product). The strong product \(G_{1}\ast G_{2}\), of two simple and connected graphs \(G_{1}\) and \(G_{2}\) is a graph with vertex set \(V (G_{1}\ast G_{2})=V(G_{1})\times V(G_{2})\) and any two vertices \((u_{1},v_{1})\) and \((u_{2},v_{2})\) are adjacent if and only if {\(u_{1}= u_{2}\in V(G_{1})\) and \(v_{1} v_{2}\in E(G_{2})\)} or {\(v_{1}= v_{2}\in V(G_{2})\) and \(u_{1} u_{2}\in E(G_{1})\)}.

Proposition 2. [15] Let \(G_1 ,G_2 \) be two graphs with \(n_1,n_2\) vertices and \(m_1,m_2\) edges, respectively. Then \[M_1 (G_1 \ast G_2 )=(n_2+6m_2)M_1 (G_1 )+8m_2 m_1+(6m_1+n_1)M_1 (G_2 )+2M_1 (G_1 ) M_1 (G_2 ).\]

Theorem 5. The \(F-index\) of the complement of \(G_1\ast G_2 \) is given by \begin{eqnarray*} F(\overline{G_1\ast G_2}) &=&n_1n_2(n_1n_2- 1)^3 – 6(m_1 n_2+n_1 m_2+2m_1 m_2)(n_1n_2- 1)^2 \\ &&+ 3(n_1n_2- 1)[(n_2+6m_2)M_1 (G_1 )+8m_2 m_1+(6m_1+n_1)M_1 (G_2 )+2M_1 (G_1 ) M_1 (G_2 )]\\ &&-[n_2 F(G_1 )+n_1 F(G_2 )+F(G_1 )F( G_2 )+6m_2 M_1 (G_1 )+6m_1 M_1 (G_2 )\\ &&+6m_2 F(G_1 )+6m_1 F(G_2 )+3F(G_2 ) M_1 (G_1 )+3F(G_1 ) M_1 (G_2 )+6M_1 (G_1 ) M_1 (G_2 )]. \end{eqnarray*}

Proof. From Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G) \), and since \(M_1 (G_1\ast G_2 )=(n_2+6m_2)M_1 (G_1 )+8m_2 m_1+(6m_1+n_1)M_1 (G_2 )+2M_1 (G_1 ) M_1 (G_2 ),\) given in Proposition 2, and by [6] we have \begin{eqnarray*} F(G_1\ast G_2 ) &=&n_2 F(G_1 )+n_1 F(G_2 )+F(G_1 )F( G_2 )+6m_2 M_1 (G_1 )+6M_1 (G_1 ) M_1 (G_2 )\\ &&+6m_1 M_1 (G_2 )+6m_2 F(G_1 )+6m_1 F(G_2 )+3F(G_2 ) M_1 (G_1 )+3F(G_1 ) M_1 (G_2 ). \end{eqnarray*} And since \( |E(G_1\ast G_2 )|=m_1 n_2+n_1 m_2+2m_1 m_2,\quad |V(G_1\ast G_2)|=n_1n_2\), given in Lemma 1. Then \begin{eqnarray*} F(\overline{G_1\ast G_2}) &=&|V(G_1\ast G_2)|(|V(G_1\ast G_2)| – 1)^3 – 6|E(G_1\ast G_2 )|(|V(G_1\ast G_2)| – 1)^2 \\ &&+ 3(|V(G_1\ast G_2)| – 1)M_1(G_1\ast G_2 ) – F(G_1\ast G_2 )\end{eqnarray*} \begin{eqnarray*} &=&n_1n_2(n_1n_2- 1)^3 – 6(m_1 n_2+n_1 m_2+2m_1 m_2)(n_1n_2- 1)^2 \\ &&+ 3(n_1n_2- 1)[(n_2+6m_2)M_1 (G_1 )+8m_2 m_1+(6m_1+n_1)M_1 (G_2 )+2M_1 (G_1 ) M_1 (G_2 )]\\ &&-[n_2 F(G_1 )+n_1 F(G_2 )+F(G_1 )F( G_2 )+6m_2 M_1 (G_1 )+6m_1 M_1 (G_2 )\\ &&+6m_2 F(G_1 )+6m_1 F(G_2 )+3F(G_2 ) M_1 (G_1 )+3F(G_1 ) M_1 (G_2 )+6M_1 (G_1 ) M_1 (G_2 )]. \end{eqnarray*}

Definition 6 (Disjunction). The disjunction \(G_{1}\vee G_{2}\) of graphs \(G_{1}\) and \(G_{2}\) is the graph with vertex set \(V(G_{1})\times V(G_{2})\) and \((u_{1},v_{1})\) is adjacent with \((u_{2},v_{2})\), whenever \((u_{1},u_{2})\in E(G_{1})\) or \((v_{1},v_{2})\in E(G_{2})\).

Theorem 6. The first Zagreb index of \(G_1\vee G_2 \) is given by \begin{eqnarray*} M_1 (G_1 \vee G_2 ) &=&[n^3_2-4n_2m_2]M_1(G_1)+[n^3_1-4n_1m_1]M_1(G_2)+ 8n_1n_2 m_1m_2+M_1(G_1)M_1(G_2). \end{eqnarray*}

Theorem 7. The \(F-index\) of the complement of \(G_1\vee G_2 \) is given by \begin{eqnarray*} F(\overline{G_1\vee G_2}) &=&n_1n_2(n_1n_2- 1)^3 – 6[m_1 {n_2}^2 +m_2 {n_1}^2 – 2m_1 m_2](n_1n_2- 1)^2 \\ &&+ 3(n_1n_2- 1)\big{[}[n^3_2-4n_2m_2]M_1(G_1)+[n^3_1-4n_1m_1]M_1(G_2)\\ &&+ 8n_1n_2 m_1m_2+M_1(G_1)M_1(G_2)\big{]}- [n_2^4 F(G_1 )+n_1^4 F(G_2 )-F(G_1 )F(G_2 )\\ &&+6n_1 n_2^2 m_2 M_1 (G_1 )+6n_2 n_1^2 m_1 M_1 (G_2 )+3n_2 F(G_1 ) M_1 (G_2 )+3n_1 F(G_2 ) M_1 (G_1 )\\ &&-6n_2^2 m_2 F(G_1 )-6n_1^2 m_1 F(G_2 )-6n_1 n_2 M_1 (G_1 ) M_1 (G_2 )]. \end{eqnarray*}

Proof. From Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G)\), and by Theorem 6 and [6], respectively, we have \begin{eqnarray*} M_1 (G_1 \vee G_2 ) &=&[n^3_2-4n_2m_2]M_1(G_1)+[n^3_1-4n_1m_1]M_1(G_2)+ 8n_1n_2 m_1m_2+M_1(G_1)M_1(G_2). \end{eqnarray*} \begin{eqnarray*} F(G_1 \vee G_2 ) &=&n_2^4 F(G_1 )+n_1^4 F(G_2 )-F(G_1 )F(G_2 )+6n_1 n_2^2 m_2 M_1 (G_1 )\\ &&+6n_2 n_1^2 m_1 M_1 (G_2 )+3n_2 F(G_1 ) M_1 (G_2 )+3n_1 F(G_2 ) M_1 (G_1 )\\ &&-6n_2^2 m_2 F(G_1 )-6n_1^2 m_1 F(G_2 )-6n_1 n_2 M_1 (G_1 ) M_1 (G_2 ). \end{eqnarray*} And since \(|E(G_1\vee G_2)|=m_1 {n_2}^2 +m_2 {n_1}^2 – 2m_1 m_2,\quad |V(G_1\vee G_2)|=n_1n_2\) given in Lemma 1. Then \begin{eqnarray*} F(\overline{G_1\vee G_2}) &=&|V(G_1\vee G_2)|(|V(G_1\vee G_2)| – 1)^3 – 6|E(G_1\vee G_2 )|(|V(G_1\vee G_2)| – 1)^2 \\ &&+ 3(|V(G_1\vee G_2)| – 1)M_1(G_1\vee G_2 ) – F(G_1\vee G_2 )\\ &=&n_1n_2(n_1n_2- 1)^3 – 6[m_1 {n_2}^2 +m_2 {n_1}^2 – 2m_1 m_2](n_1n_2- 1)^2 \\ &&+ 3(n_1n_2- 1)\big{[}[n^3_2-4n_2m_2]M_1(G_1)+[n^3_1-4n_1m_1]M_1(G_2)\\ &&+ 8n_1n_2 m_1m_2+M_1(G_1)M_1(G_2)\big{]}- [n_2^4 F(G_1 )+n_1^4 F(G_2 )-F(G_1 )F(G_2 )\\ &&+6n_1 n_2^2 m_2 M_1 (G_1 )+6n_2 n_1^2 m_1 M_1 (G_2 )+3n_2 F(G_1 ) M_1 (G_2 )+3n_1 F(G_2 ) M_1 (G_1 )\\ &&-6n_2^2 m_2 F(G_1 )-6n_1^2 m_1 F(G_2 )-6n_1 n_2 M_1 (G_1 ) M_1 (G_2 )]. \end{eqnarray*}

Definition 7 (Symmetric difference). The symmetric difference \(G_{1}\oplus G_{2}\), of two simple and connected graphs \(G_{1}\) and \(G_{2}\) is the graph with vertex set \(V(G_{1})\times V(G_{2})\) and \(E(G_{1}\oplus G_{2})=(u_{1},u_{2})(v_{1},v_{2} )| u_{1} v_{1}\in E(G_{1})\) or \(u_{2} v_{2}\in E(G_{2})\) but not both.

Theorem 8. The first Zagreb index of \(G_1\oplus G_2 \) is given by \begin{eqnarray*} M_1 (G_1 \oplus G_2 ) &=&[n^3_2-8n_2m_2]M_1(G_1)+[n^3_1-8n_1m_1]M_1(G_2)+ 8n_1n_2 m_1m_2+4M_1(G_1)M_1(G_2). \end{eqnarray*}

Theorem 9. The \(F-index\) of the complement of \(G_1\oplus G_2 \) is given by \begin{eqnarray*} F(\overline{G_1\oplus G_2}) &=&n_1n_2(n_1n_2- 1)^3-6[m_1 {n_2}^2 + m_2 {n_1}^2 – 4m_1 m_2](n_1n_2- 1)^2 \\ &&+ 3(n_1n_2- 1)\big{[}[n^3_2-8n_2m_2]M_1(G_1)+[n^3_1-8n_1m_1]M_1(G_2)\\ &&+ 8n_1n_2 m_1m_2+4M_1(G_1)M_1(G_2)\big{]}- \big{[}n_2^4 F(G_1 )+n_1^4 F(G_2 )\\ &&-8F(G_1 )F(G_2 )+6n_1 n_2^2 m_2 M_1 (G_1 )+6n_2 n_1^2 m_1 M_1 (G_2 )\\ &&+12n_2 F(G_1 ) M_1 (G_2 )+12n_1 F(G_2 ) M_1 (G_1 )-12n_2^2 m_2 F(G_1 )\\ &&-12n_1^2 m_1 F(G_2 )-12n_1 n_2 M_1 (G_1 ) M_1 (G_2)\big{]}. \end{eqnarray*}

Proof. From Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 6m(n – 1)^2 + 3(n – 1)M_1(G) – F(G)\), and by Theorem 8 and [6], respectively, we have \begin{eqnarray*} M_1 (G_1 \oplus G_2 ) &=&[n^3_2-8n_2m_2]M_1(G_1)+[n^3_1-8n_1m_1]M_1(G_2)+ 8n_1n_2 m_1m_2+4M_1(G_1)M_1(G_2). \end{eqnarray*} \begin{eqnarray*} F(G_1 \oplus G_2 ) &=&n_2^4 F(G_1 )+n_1^4 F(G_2 )-8F(G_1 )F(G_2 )+6n_1 n_2^2 m_2 M_1 (G_1 )\\ &&+6n_2 n_1^2 m_1 M_1 (G_2 )+12n_2 F(G_1 ) M_1 (G_2 )+12n_1 F(G_2 ) M_1 (G_1 )\\ &&-12n_2^2 m_2 F(G_1 )-12n_1^2 m_1 F(G_2 )-12n_1 n_2 M_1 (G_1 ) M_1 (G_2 ). \end{eqnarray*} And since \( |E(G_1\oplus G_2 )|=m_1 {n_2}^2 + m_2 {n_1}^2 – 4m_1 m_2,\quad |V(G_1\oplus G_2)|=n_1n_2\) given in Lemma 1. Then \begin{eqnarray*} F(\overline{G_1\oplus G_2}) &=&|V(G_1\oplus G_2)|(|V(G_1\oplus G_2)| – 1)^3 – 6|E(G_1\oplus G_2 )|(|V(G_1\oplus G_2)| – 1)^2 \\ &&+ 3(|V(G_1\oplus G_2)| – 1)M_1(G_1\oplus G_2 ) – F(G_1\oplus G_2 )\\ &=&n_1n_2(n_1n_2- 1)^3-6[m_1 {n_2}^2 + m_2 {n_1}^2 – 4m_1 m_2](n_1n_2- 1)^2 \\ &&+ 3(n_1n_2- 1)\big{[}[n^3_2-8n_2m_2]M_1(G_1)+[n^3_1-8n_1m_1]M_1(G_2)\\ &&+ 8n_1n_2 m_1m_2+4M_1(G_1)M_1(G_2)\big{]}- \big{[}n_2^4 F(G_1 )+n_1^4 F(G_2 )\\ &&-8F(G_1 )F(G_2 )+6n_1 n_2^2 m_2 M_1 (G_1 )+6n_2 n_1^2 m_1 M_1 (G_2 )\\ &&+12n_2 F(G_1 ) M_1 (G_2 )+12n_1 F(G_2 ) M_1 (G_1 )-12n_2^2 m_2 F(G_1 )\\ &&-12n_1^2 m_1 F(G_2 )-12n_1 n_2 M_1 (G_1 ) M_1 (G_2)\big{]}. \end{eqnarray*}

4. Application

In this section, the forgotten index have been investigated for complement titania \(TiO_2\) nanotubes and molecular graph of nanotorus.

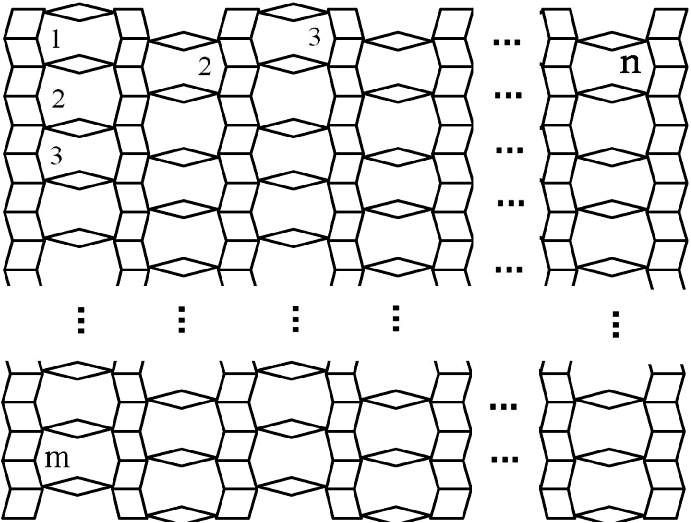
Corollary 1. The forgotten index of complement \(TiO_2 [n,m]\) nanotube Figure 1 is given by \begin{eqnarray*} F (\overline{TiO_2[n,m]}) &=&(6mn+ 6n)(6mn+ 6n- 1)^3 – 4(10mn+8n)(6mn+ 6n- 1)^2 \\ &&+ 3(6mn+ 6n- 1)(76mn + 48n) – 320mn – 160n . \end{eqnarray*}

Proof. By Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 4m(n – 1)^2 + 3(n – 1)M_1(G) – F(G)\), and since \(F(TiO_2 [n,m] )=320mn + 160n\), and \(M_1 (TiO_2 [n,m] )=76mn + 48n\) given in [16]. In [17] the partitions of the vertex set and edge set \(\sum| V(TiO_2[n,m])|=6mn+ 6n\), \(\sum| E(TiO_2[n,m])|=10mn+8n\) of titania nanotubes. Then \begin{eqnarray*} F (\overline{TiO_2[n,m]}) &=&\sum| V(TiO_2[n,m])|(\sum| V(TiO_2[n,m])| – 1)^3- 4\sum| E(TiO_2[n,m])|(\sum| V(TiO_2[n,m])| – 1)^2 \\ &&+ 3(\sum| V(TiO_2[n,m])| – 1)M_1(TiO_2[n,m]) – F(TiO_2[n,m])\\ &=&(6mn+ 6n)(6mn+ 6n- 1)^3 – 4(10mn+8n)(6mn+ 6n- 1)^2 \\ &&+ 3(6mn+ 6n- 1)(76mn + 48n) – 320mn – 160n .

Corollary 2. Let \(T = T [p, q]\) be the molecular graph of a nanotorus such that \(|V (T )|=pq\), \(|E (T )|=\frac{3}{2} pq\), Figure 2. Then

• a. \(F (\overline{T [p, q]} )=pq[(pq- 1)^2( pq- 7) + 27(pq- 1)- 27] .\)
• b. \( F (P_n\times T)= pq [125n-122] .\)
• c. \(F( \overline {P_n\times T})=pq[(npq- 1)^2(n^2pq-11n+4)+ 3(npq- 1)(25n-18) -125n+122].\)

Proof.

• a. By Proposition 1, we have \(F (\overline{G} )= n(n – 1)^3 – 4m(n – 1)^2 + 3(n – 1)M_1(G) – F(G)\), and since \(M_1 (T ) =9 pq \) given in [14]. and \(F (T ) =27 pq \) given in [18]. Then \begin{eqnarray*} F (\overline{T [p, q]} ) &=& |V (T )|(|V (T )| – 1)^3 – 4|E(T )|(|V (T )| – 1)^2 + 3(|V (T )| – 1)M_1(T) – F(T)\\ &=& pq(pq- 1)^3 – 6 pq(pq- 1)^2 + 27 pq(pq- 1)- 27 pq \\ &=& pq[(pq- 1)^2( pq- 7) + 27(pq- 1)- 27] . \end{eqnarray*}
• b. By \(F(G_1\times G_2 )=n_2 F(G_1 )+n_1 F( G_2 )+6m_2 M_1 (G_1 )+6m_1 M_1 (G_2 ),\) given in [6]. and since \(M_1 (P_n ) =4n-6 \), \(M_1 (T ) =9 pq \) given in [14]. and \(F (P_n ) =8n-14 \), \(F (T ) =27 pq \) given in [18]. Then \begin{eqnarray*} F (P_n \times T ) &=& |V (T )| F(P_n )+|V (P_n )| F( T )+6|E (T )| M_1 (P_n )+6|E (P_n )| M_1 (T )\\ &=& 2pq (4n-7)+27npq+18pq (2n-3)+54pq(n-1)\\ &=& pq [125n-122]. \end{eqnarray*}
• c. By [19], \(M_1 (P_n\times T ) =pq(25n-18),\) and by using Lemma 1, \(|E(P_n \times T)| =pq(\frac{5}{2}n-1)\), \(|V(P_n \times T)| =npq \), and applying Proposition 1 and item (b) we get \begin{eqnarray*} F (\overline{P_n \times T} ) &=& |V (P_n \times T )|(|V (P_n \times T )| – 1)^3 – 4|E(P_n \times T)|(|V (P_n \times T )| – 1)^2\\ &&+ 3(|V (P_n \times T )| – 1)M_1(P_n \times T) – F(P_n \times T)\\ &=& npq(npq- 1)^3 – 4pq(\frac{5}{2}n-1)(npq- 1)^2 \\ &&+ 3pq(npq- 1)(25n-18) -pq [125n-122]\\ &=& pq[(npq- 1)^2(n^2pq-11n+4)+ 3(npq- 1)(25n-18) -125n+122]. \end{eqnarray*}

5. Conclusion

The forgotten index one of the most important topological indices which preserve the symmetry of molecular structures and provide a mathematical formulation to predict their physical and chemical properties. In this article, we computed the forgotten index of some basic mathematical operations and obtained explicit formula for their values under complement graph operations, and we computed the forgotten index of molecular complement graph of nanotorus and titania nanotubes \(TiO_2 [n,m]\).

Authorcontributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflictofinterests

The authors declare no conflict of interest.