Let \(G\) be a simple graph. A total dominator coloring of \(G\) is a proper coloring of the vertices of \(G\) in which each vertex of the graph is adjacent to every vertex of some color class. The total dominator chromatic number \(\chi_d^t(G)\) of \(G\) is the minimum number of colors among all total dominator coloring of \(G\). In this paper, we study the total dominator chromatic number of some graphs with specific construction. Also we compare \(\chi_d^t(G)\) with \(\chi_d^t(G-e)\), where \(e\in E(G)\).
In this paper, we are concerned with simple finite graphs, without direction, multiple, or weighted edges, and without self-loops. Let \(G=(V,E)\) be such a graph and \(\lambda \in \mathbb{N}\). A mapping \(f : V (G)\longrightarrow \{1, 2,…,\lambda\}\) is called a \(\lambda\)-proper coloring of \(G\) if \(f(u) \neq f(v)\) whenever the vertices \(u\) and \(v\) are adjacent in \(G\). A color class of this coloring is a set consisting of all those vertices assigned the same color. If \(f\) is a proper coloring of \(G\) with the coloring classes \(V_1, V_2,…, V_{\lambda}\) such that every vertex in \(V_i\) has color \(i\), then we write simply \(f = (V_1,V_2,…,V_{\lambda})\). The chromatic number \(\chi(G)\) of \(G\) is the minimum number of colors needed in a proper coloring of a graph. The concept of a graph coloring and chromatic number is very well-studied in graph theory. A dominator coloring of \(G\) is a proper coloring of \(G\) such that every vertex of \(G\) dominates all vertices of at least one color class (possibly its own class), i.e., every vertex of \(G\) is adjacent to all vertices of at least one color class. The dominator chromatic number \(\chi_d(G)\) of \(G\) is the minimum number of color classes in a dominator coloring of \(G\).
The concept of dominator coloring was introduced and studied by Gera, Horton and Rasmussen [1]. Let \(G\) be a graph with no isolated vertex, then the total dominator coloring (TD-coloring) is a proper coloring of \(G\) in which each vertex of the graph is adjacent to every vertex of some (other) color class [2]. The total dominator chromatic number (TDC-number), \(\chi_d^t(G)\) of \(G\) is the minimum number of color classes in a TD-coloring of \(G\). The TDC-number of a graph is related to its total domination number. A total dominating set of \(G\) is a set \(S\subseteq V(G)\) such that every vertex in \(V(G)\) is adjacent to at least one vertex in \(S\). The total domination number of \(G\), denoted by \(\gamma_t(G)\), is the minimum cardinality of a total dominating set of \(G\). A total dominating set of \(G\) of cardinality \(\gamma_t(G)\) is called a \(\gamma_t(G)\)-set.
The literature on the subject on total domination in graphs was surveyed and detailed in the book [3]. It is not hard to see that for every graph \(G\) with no isolated vertex, \(\gamma_t(G) \leq \chi_d^t(G)\). Computation of the TDC-number is NP-complete. The TDC-number of some operations of two graphs was studied in [2]. Also Henning in [4] established the lower and upper bounds on the TDC-number of a graph in terms of its total domination number. He showed that, for every graph \(G\) with no isolated vertex satisfies \(\gamma_t(G) \leq \chi_d^t (G)\leq \gamma_t(G) + \chi(G)\). The properties of TD-colorings in trees was studied in [4]. Trees \(T\) with \(\gamma_t(T) =\chi_d^t(T)\) was characterized in [4].
The join \(G = G_1 + G_2\) of two graph \(G_1\) and \(G_2\) with disjoint vertex sets \(V_1\) and \(V_2\) and edge sets \(E_1\) and \(E_2\) is the graph union \(G_1\cup G_2\) together with all the edges joining \(V_1\) and \(V_2\). For two graphs \(G = (V,E)\) and \(H=(W,F)\), the corona \(G\circ H\) is the graph arising from the disjoint union of \(G\) with \(| V |\) copies of \(H\), by adding edges between the \(i\)th vertex of \(G\) and all vertices of \(i\)th copy of \(H\).
In this paper, we continue the study of TD-colorings in graphs. We compute the TDC-number of some specific graphs in the Section 2. In Section 3, we study TD-chromatic number of corona and join of graphs.
Theorem 1. If \(P_n\) is the path graph of order \(n\geq 8\), then \[ \chi_d^t(P_n)=\left\{ \begin{array}{ll} {\displaystyle 2k+2}& \quad\mbox{if \(n=4k\), }\\ {\displaystyle 2k+3}& \quad\mbox{if \(n=4k+1\),}\\ {\displaystyle 2k+4}& \quad\mbox{if \(n=4k+2\), \(n=4k+3\).}\\ \end{array} \right. \] Also \( \chi _ d^t (P_3)=2\), \( \chi _ d^t (P_4)= 3\), \(\chi _ d^t (P_5)= \chi _ d^t (P_6)=4\) and \( \chi _ d^t (P_7)=5\).
Proof. It is easy to show that \( \chi _ d^t (P_3)=2\), \( \chi _ d^t (P_4)= \chi _ d^t (P_5)=3\), \( \chi _ d^t (P_6)=4\) and \( \chi _ d^t (P_7)=5\). Now let \(n\geq 8\). First we show that for each four consecutive vertices we have to use at least two new colors. Consider Figure 1. We have two cases. If we give an old color to \(v_{i+1}\), then we need to give a new color to \(v_{i+2}\) and \(v_{i+3}\) to have a TD-coloring. Also if we give a new color to \(v_{i+1}\), then we have to give a new color to \(v_{i+2}\) or \(v_{i}\) to have a TD-coloring. So we need at least two new colors in every four consecutive vertices.
Suppose that \(n=4k\), for some \(k\in \mathbb{N}\). We give a TD-coloring for the path \(P_{4k}\) which use only two new colors in every four consecutive vertices. Define a function \(f_0\) on the vertices of \(P_{4k}\), i.e., \(V(P_{4k})\) such that for any vertex \(v_i\),
\[f_0(v_i)=\left\{
\begin{array}{ll}
{\displaystyle
1} &
\quad\mbox{if \(i=1+4k\),}\\
{\displaystyle
2} &
\quad\mbox{if \(i=4k\),}
\end{array}
\right.\]
and for any \(v_i\) , \(i \neq 4k\) and \(i\neq 4k+1\), \(f_0(v_i)\) is a new number. Then \(f_0\) is a TD-coloring of \(P_{4k}\) with the minimum number \(2k+2\).

If \(n=4k+2\), for some \(k\in \mathbb{N}\), then first color the \(4k-4\) vertices using \(f_0\). Now for the rest of vertices define \(f_2(v_{4k-3})=1\), \(f_2(v_{4k-2})=2k+1\), \(f_2(v_{4k-1})=2k+2\), \(f_2(v_{4k})=2k+3\), \(f_2(v_{4k+1})=2k+4\) and \(f_2(v_{4k+2})=2\). Since for every six consecutive vertices we have to use at least four new colors, so \(f_2\) is a TD-coloring of \(P_{4k+2}\) with the minimum number \(2k+4\).
If \(n=4k+3\), for some \(k\in \mathbb{N}\), then first color the \(4k-4\) vertices using \(f_0\). Now for the rest of vertices define \(f_3(v_{4k-3})=1\), \(f_3(v_{4k-2})=2k+1\), \(f_3(v_{4k-1})=2k+2\), \(f_3(v_{4k})=2\), \(f_3(v_{4k+1})=2k+3\), \(f_3(v_{4k+2})=2k+4\) and \(f_3(v_{4k+2})=2\). Then \(f_3\) is a TD-coloring of \(P_{4k+2}\) with the minimum number \(2k+4\). Therefore we have the result.
Theorem 2. Let \(C_n\) be the cycle graph of order \(n\geq 8\). Then \[ \chi _ d^t (C_n)=\left\{ \begin{array}{ll} {\displaystyle 2k+2} & \quad\mbox{if \(n=4k\),}\\ {\displaystyle 2k+3}& \quad\mbox{if \(n=4k+1\),}\\ {\displaystyle 2k+4}& \quad\mbox{if \(n=4k+2\), \(n=4k+3\).} \end{array} \right. \] Also \( \chi _ d^t (C_3)=3\), \( \chi _ d^t (C_4)=2\), \( \chi _ d^t (C_5)= \chi _ d^t (P_6)=4\) and \( \chi _ d^t (C_7)=5\).
Proof. Observe that \(\chi_d^t(C_3)=3\), \( \chi_d^t (C_4)=2\), \( \chi_d^t (C_5)= \chi_d^t (C_6)=4\) and \( \chi_d^t (C_7)=5\). Now let \(n\geq 8\). It is sufficient to give a TD-coloring to the \(P_n\) as we see in the proof of the Theorem 1, then we add an edge between vertices \(v_1\) and \(v_n\). Then we have a TD-coloring for \(C_n\) and the result follows.
From Theorems 1 and 2, we have the following corollary.Corollary 1. For every \(n\geq6\), \(\chi _ d^t (P_n)=\chi _ d^t (C_n)\).
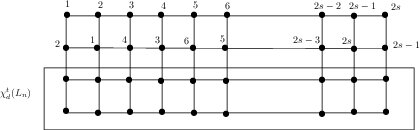
Here we consider the ladder graph. We need the definition of Cartesian product of two graphs. Given any two graphs \(G\) and \(H\), we define the Cartesian product, denoted \(G\Box H\), to be the graph with vertex set \(V(G)\times V(H)\) and edges between two vertices \((u_1, v_1)\) and \((u_2,v_2)\) if and only if either \(u_1 = u_2\) and \(v_1v_2 \in E(H)\) or \(u_1u_2 \in E(G)\) and \(v_1 = v_2\).Theorem 3. For every \(n\geq 2\), \[ \chi_d^t(L_n)=\left\{ \begin{array}{lr} {\displaystyle n+1}&\quad\mbox{if \(n\) is odd,}\\ {\displaystyle n}& \quad\mbox{if \(n\) is even.} \end{array} \right. \]
Proof.
Let \(x_{ij}\) be a vertex of ladder graph in \(i\)-th row and \(j\)-th column (\(1\leq i\leq 2\) and \(1\leq j\leq n\)). If \(n=2k+1\) for some \(k\in \mathbb{N}\), then we color the vertex \(x_{1j}\) with color \(j\) and for vertices \(x_{2j}\) we assign the color \(2j+2\) for \(x_{2(2j+1)}\) and color \(2j-1\) for vertex \(x_{2(2j)}\) (Figure 2). This coloring gives a TD-coloring for \(L_n\) and this method warranty the least number of used colors. So \(\chi_d^t(L_{2k+1})=2k+2\). With similar argument we have the result for even \(n\).

I am raw html block.
Click edit button to Here, we generalize the ladder graph \(P_2\Box P_n\) to grid graphs \(P_n\Box P_m\). The following theorem gives the TDC-number of grid
graphs:
Theorem 4. Let \(m,n\geq 2\). The TDC-number of grid graphs \(P_n\Box P_m\) is, \[ \chi_d^t(P_n\Box P_m)=\left\{ \begin{array}{lr} {\displaystyle k \chi_d^t(P_n\Box P_2)=k\chi_d^t(L_n)}&\quad\mbox{if \(m=2k\) and \(n=2s\),}\\ {\displaystyle k\chi_d^t(L_n)+\chi_d^t(P_n)}& \quad\mbox{if \(m=2k+1\) and \(n=2s\),}\\ {\displaystyle s\chi_d^t(L_m)+\chi_d^t(P_m)}& \quad\mbox{if \(m=2k\) and \(n=2s+1\),}\\ {\displaystyle \chi_d^t(P_{n-1}\Box P_{m-1})+\chi_d^t(P_{m+n-1})}& \quad\mbox{if \(m=2k+1\) and \(n=2s+1\).} \end{array} \right. \]
Proof.
We prove two first cases. The proof of another cases are similar. Suppose that \(m=2k\) and \(n=2s\), for some \(k\) and \(s\). We use induction on
\(m\).
Case 1. If \(m=2\) and \(n=2s\), then we have a ladder and the result follows from Theorem 3. For \(m=2\), as you see in Figure 3, we have two \(L_n\) as subgraphs of \(4\times n\) grid graph. Since in TD-coloring of \(4\times n\) grid graph, we can not use the colors of vertices in the first ladder, for the second ladder, so we need \(2\chi_d^t(L_n)\) colors. It is easy to see that we cannot use less colors. Since in the \(P_n\Box P_{2k}\), there are exactly \(k\) ladder \(L_n\) as subgraphs, we have the result by induction hypothesis.this html
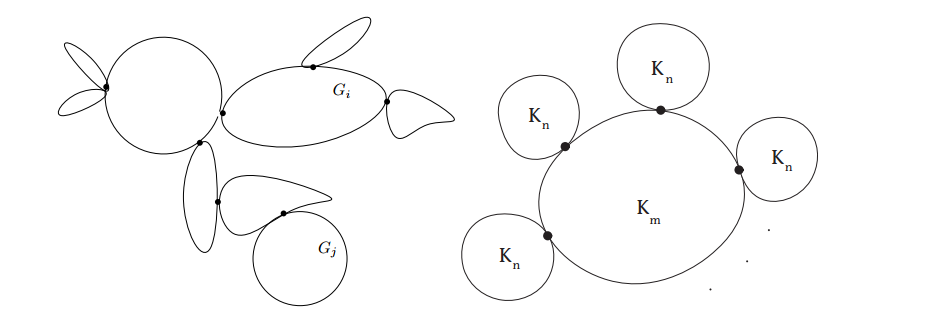
Theorem 5. Let \(m,n\geq 2\) be integers. For the graph \(Q(m,n)\) we have: $$\chi_d^t(Q(m,n))=m+n-1.$$
Proof. We need colors \(1,2,\ldots,m\) to color the complete graph \(K_m\). Now for the rest of vertices of \(Q(m,n)\), we use colors \(m+1,m+2,\ldots,m+n-1\) in each \(K_n\). This gives a TD-coloring for \(Q(m,n)\). We shall show that we are not able to have TD-coloring with less colors. Suppose that we omit one color class between numbers \(m+1,m+2,\ldots,m+n-1\). Consider one copy of \(K_n\) and simply call it \(G_1\) and call the vertex which has no color as \(v\). We have to use one color from the numbers \(1,2,\ldots,m\) to color \(v\). Suppose that this color is \(i\), where \(1\leq i\leq m\). Then there is another copy of \(K_n\), say \(G_2\) which has a vertex with color \(i\) (point attached vertex). Also there is \(w \in V(G_2)\) such that has no color. We cannot color \(w\) with \(m+1,m+2,\ldots,m+n-1\). Since \(w\) is not adjacent to \(v\), so it cannot get an arbitrary color from \(1,2,\ldots,m\). Therefore we have to change the color of a vertex \(s\in V(G_2)-\{w\}\) to \(j \in \{1,2,\ldots,m\}\). But \(w\) is not adjacent to the vertex with color \(j\) in \(K_m\). So we cannot give the vertex \(w\) any color. By the same argument we cannot omit two color classes and so on. Therefore \(\chi_d^t(Q(m,n))=m+n-1\).
Let to consider a special cases of point attaching of \(k\) graphs. Let \(G_1,G_2,…, G_k\) be a finite sequence of pairwise disjoint connected graphs and let \(x_i, y_i\in V (G_i)\). The link \(G\) of the graphs \(\{G_i\}_{i=1}^k\) with respect to the vertices \(\{x_i, y_i\}_{i=1}^k\) is obtained by adding an edge which connect the vertex \(y_i\) of \(G_i\) with the vertex \(x_{i+1}\) of \(G_{i+1}\) for all \(i = 1, 2,…, k-1\), see Figure 5, [6].
Theorem 6. Let \(G\) be a graph obtained by point attaching from \(G_1,…,G_k\). Then $$\chi_d^t(G)\leq\chi_d^t(G_1)+\chi_d^t(G_2)+\ldots + \chi_d^t(G_n).$$
Proof. Since we can use numbers \(1,2,\ldots, \chi_d^t(G_1)\) for \(G_1\) and use numbers \( \chi_d^t(G_1)+1, \chi_d^t(G_1)+2,\ldots, \chi_d^t(G_1)+ \chi_d^t(G_2)\) for \(G_2\) and continue this process, then we have a TD-coloring . Therefore we have the result.
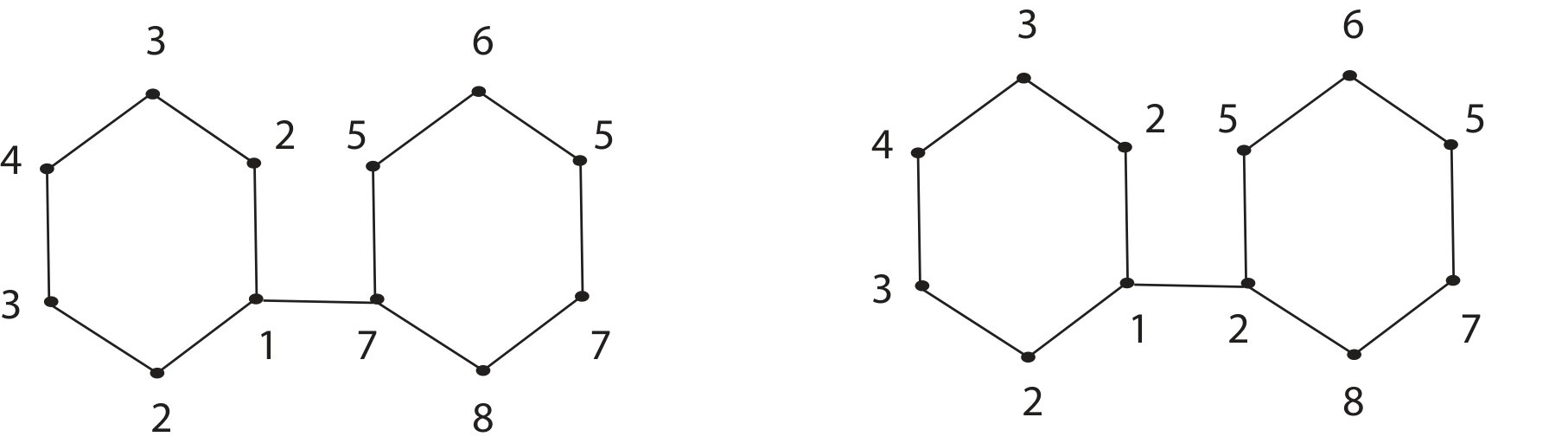
We shall show that the upper bound in Theorem 6 is sharp. For this reason, we consider a special kind of link graph has shown in Figure 5.Theorem 7. For the graph \(L_{6,2,n}\) in Figure 5 we have: $$\chi_d^t(L_{6,2,n})=4n.$$
Proof.
We color the vertices of \(L_{6,2,n}\) with numbers \(1,2,3,…,4n\), as shown in the Figure 5. Observe that, we need \(4n\) color for TD-coloring. We shall show that we are not able to have TD-coloring with less colors. Note that \(L_{6,2,1}\) is \(C_6\) and \(\chi_d^t(C_6)=4\). Now we consider \(L_{6,2,2}\).
Two kinds of coloring of \(L_{6,2,2}\) has shown in Figure 6.
Theorem 8. If \(G\) is a connected graph, and \(e=vw\in E(G)\) is not a bridge, then $$\chi_d^t(G-e)\leq \chi_d^t(G)+2 .$$
Proof.
Suppose that the vertex \(v\) has color \(i\) and the vertex \(w\) has color \(j\). We have the following cases:
Case 1. The vertex \(v\) does not use the color class \(j\) and the vertex \(w\) does not use the color class \(i\) in the TD-coloring of \(G\). So the TD-coloring of \(G\) gives a TD-coloring of \(G-e\). Therefore \(\chi_d^t(G-e)\leq \chi_d^t(G)\). In this case \(\chi_d^t(G-e)=\chi_d^t(G)\).
Case 2. The vertex \(v\) uses the color class \(j\) but the vertex \(w\) does not use the color class \(i\) in the TD-coloring of \(G\). Since the vertex \(v\) used the color class \(j\) for The TD-coloring then we have two cases:
Theorem 9.
Proof.
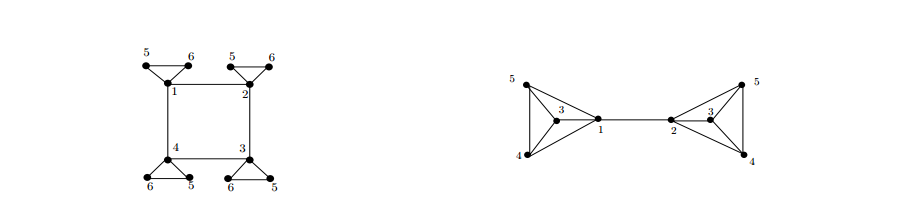
Remark 1 The upper bound for \(\chi_d^t(G\circ H)\) in Theorem 9(iii) is a sharp bound. As examples, for the graph \(C_4\circ K_2\) and \(K_2\circ K_3\) we have the equality (Figure 7).
Theorem 10. Let \(G\) and \(H\) be two connected graphs, \(\vert V(G) \vert\geq 2 \) and \(\vert V(H) \vert\geq 2\) , then $$\chi_d^t(G+H)=\chi_d^t(G)+\chi_d^t(H).$$
Proof. For the TD-coloring of \(G+H\), the colors of vertices of \(G\) cannot be used for the coloring of vertices of \(H\), and the colors of the vertices of \(H\) cannot use for coloring of the vertices of \(G\), so $$\chi_d^t(G+H)\geq \chi_d^t(G)+\chi_d^t(H).$$ Now, it suffices to consider the coloring of \(G\) and the coloring of \(H\) in the TD-coloring of \(G+H\). Therefore, we have the result.
