Chemical reaction network theory is an area of applied mathematics that attempts to model the behavior of real world chemical systems. Since its foundation in the 1960s, it has attracted a growing research community, mainly due to its applications in biochemistry and theoretical chemistry. It has also attracted interest from pure mathematicians due to the interesting problems that arise from the mathematical structures involved. It is experimentally proved that many properties of the chemical compounds and their topological indices are correlated. In this report, we compute closed form of forgotten polynomial and forgotten index for interconnection networks. Moreover we give graphs to see dependence of our results on the parameters of structures.
In mathematical chemistry, mathematical tools such as polynomials and numbers predict properties of compounds without using quantum mechanics. These tools, in combination, capture information hidden in the symmetry of molecular graphs. Most commonly known invariants of such kinds are degree-based topological indices. These are the numerical values that correlate the structure with various physical properties, chemical reactivity and biological activities [1, 2, 3, 4, 5]. It is an established fact that many properties such as heat of formation, boiling point, strain energy, rigidity and fracture toughness of a molecule are strongly connected to its graphical structure and this fact plays a synergic role in chemical graph theory.
The butterfly graphs are considered as the principal graphs of FFT(Fast Fourier Transforms) networks and it is efficient in performing FFT. In butterfly networks the series of switch stages and interconnection patterns that allow \(n\) inputs and \(n\) outputs to be inter linked with each other. The Benes network is comprises of continues butterflies and is known as permutation routing whereas butterfly network is identified as Fast Fourier transforms [6]. Butterfly network and Benes network contains important multistage interconnection networks that comprises of attractive topologies for communication networks [7]. Further these topologies are helpful in parallel computing systems which are IBM,SP1/SP2, MIT transit project, internal structures of optical couplers [8, 9 ].
For the connection of numerous homogenously replicated processes multiprocessor interconnection networks are important which is also called a processing node. Message passing is mostly used for the management and communication between processing nodes for program execution. Planning and using of multiprocessor interconnection networks have significant consideration due to the availability of powerful microprocessors and memory chips [10]. For the extreme parallel computing, multipurpose interconnection mesh networks are widely known. This is the fact that these networks having topologies which reproduce the communication pattern of a wide variety regarding natural problems. Mesh networks have recently received a lot of attention for better scalability to larger networks as compared to hyper cubes [11].
A graph with vertex set \(V(G)\) and edge set \(E(G)\) is connected, if there exist a connection between any pair of vertices in \(G\). The distance between two vertices \(u\) and \(v\) is denoted as \(d(u,v)\) and is the length of shortest path between \(u\) and \(v\) in graph \(G\). The number of vertices of \(G\), adjacent to a given vertex \(v\), is the \emph{degree} of this vertex, and will be denoted by \(d_{v}\). For details on basics of graph theory, any standard text such as [12] can be of great help.
The topological index of a molecule structure can be considered as a non-empirical numerical quantity which quantifies the molecular structure and its branching pattern in many ways. In this point of view, the topological index can be regarded as a score function which maps each molecular structure to a real number and is used as a descriptor of the molecule under testing. Topological indices [13, 14, 15, 16, 17, 18, 19, 20, 21, 22] gives a good predictions of variety of physico-chemical properties of chemical compounds containing boiling point, heat of evaporation, heat of formation, chromatographic retention times, surface tension, vapor pressure etc. Since the 1970s, two degree based graph invariants have been extensively studied. These are the first Zagreb index \(M_{1}\) and the second Zagreb index \(M_{2}\) [23, 24] and defined as: \(M_{1}(G)=\sum\limits_{v\in V(G)}(d_{v})^2\) and \(M_{2}(G)=\sum\limits_{usv\in V(G)}d_{u}d_{v}\).
In this article, we compute closed form of the forgotten polynomial for interconnection networks. We also computed forgotten index of these networks. For detailed study about degree-based topological indices, we refer [25, 26, 27, 28, 29, 30] and the references therein.
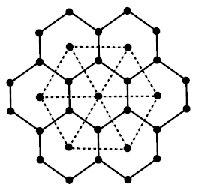
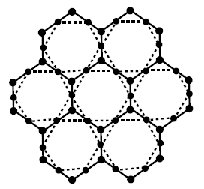
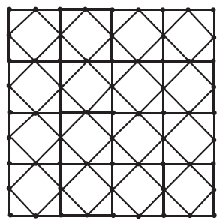
Under this section two new architectures are introduced by using \(m \times n\) mesh network, the defining parameters \(m\) and \(n\) are the number of vertices in any column and row. The restricted dual of Mesh \(m \times n\) is \(m-1 \times n-1\) can be easily noticed. By applying medial operation on mesh \(m{\rm \; \times\; n}\) and deleting the vertex of unrestrained face we found the restricted medial of mesh \(m{\rm \; \times\; n}\). By taking union \(m{\rm \; \times\; n}\) mesh and its restricted medial in a way that the vertices of restricted medial are placed in the middle of each edge of \(m{\rm \; x\; n}\) mesh, the resulting architecture will be the planar named as mesh derived network of first type \(MDN1[m,n]\) network as depicted in Fig. 6. The vertex and edge cardinalities of \(MDN1[m,n]\) network are \(3mn-m-n\) and \(8mn-6(m+n){\rm +}4\) respectively. The second architecture is obtained from the union of \(m{\rm \; \times\; n}\) mesh and its restricted dual \(m-1{\rm \; }\times{\rm \;}n-1\) mesh by joining each vertex of \(m-1{\rm \; }\times{\rm \; }n-1\) mesh to each vertex of parallel face of \(m{\rm \; \times\; n}\) mesh. The resulting architecture will be mesh derived network of second type \(MDN2[m,n]\) network as depicted in Figure 17. The number of vertices and edges of this non planar graph are \(2mn-m-n+1\) and \(8(mn-m-n+1)\) respectively. Some other types of mesh derived networks are well-defined and considered in [31]. The main graph parameter which is discussed in [31] for mesh derived networks is the metric dimension of networks. Now we compute topological indices of these mesh derived networks
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,4)\) | \(8\) |
| \((3,4)\) | \(4(m+n-4)\) |
| \((3,6)\) | \(2(m+n-4)\) |
| \((4,6)\) | \(4(mn-n-m)\) |
| \((4,4)\) | \(4\) |
| \((6,6)\) | \(4(mn-2m-2n+4)\) |
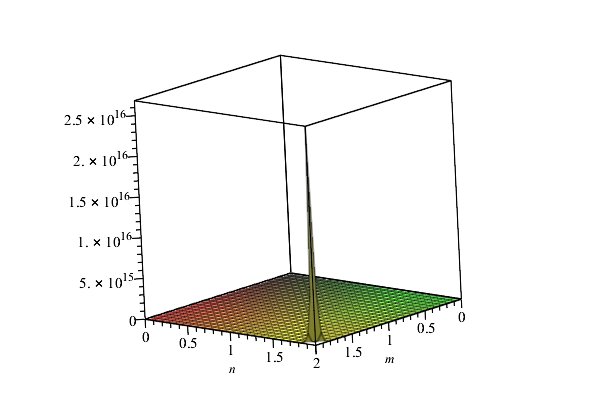
From the definition of forgotten index we have \begin{eqnarray*} F(MDN1[m,n])&=&\prod _{uv\in E(MDN1[m,n])}[du^{2} +dv^{2} ] \\ &=& \prod _{uv\in E_{1} (MDN1[m,n])}[du^{2} +dv^{2} ]\\ &&\times \prod _{uv\in E_{2} (MDN1[m,n])}[du^{2} +dv^{2} ]\\ &&\times \prod _{uv\in E_{3} (MDN1[m,n])}[du^{2} +dv^{2} ] \\ &&\times \prod _{uv\in E_{4} (MDN1[m,n])}[du^{2} +dv^{2} ] \\ &&\times \prod _{uv\in E_{5} (MDN1[m,n])}[du^{2} +dv^{2} ]\\ && \times \prod _{uv\in E_{6} (MDN1[m,n])}[du^{2} +dv^{2} ] \\ &=& 20^{\left|E_{1} (MDN1[m,n])\right|} \times 25^{\left|E_{2} (MDN1[m,n)\right|}\\ &&\times 45^{\left|E_{3} (MDN1[m,n])\right|} \times 52^{\left|E_{4} (MDN1[m,n])\right|}\\ && \times 32^{\left|E_{5} (MDN1[m,n])\right|} \times 72^{\left|E_{6} (MDN1[m,n])\right|} \\ &=& 20^{8} \times 25^{4(m+n-4)} \times 45^{2(m+n-4)} \times 52^{4(mn-m-n)}\\ && \times 32^{4} \times 72^{4(mn-2m-2n+4)} \end{eqnarray*}
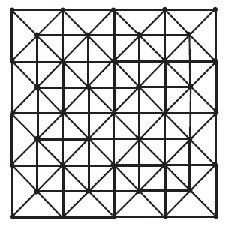
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((3,6)\) | \(4\) |
| \((3,5)\) | \(8\) |
| (5,6) | \(8\) |
| \((5,5)\) | \(2(m+n-6)\) |
| \((6,8)\) | 4 |
| \((5,8)\) | \(2(m+n-4)\) |
| \((5,7)\) | \(4(m+n-6)\) |
| \((7,7)\) | \(2(m+n-8)\) |
| \((6,7)\) | \(8\) |
| \((7,8)\) | \(6(m+n-6)\) |
| \((8,8)\) | \(8mn-24(m+n)+72\) |
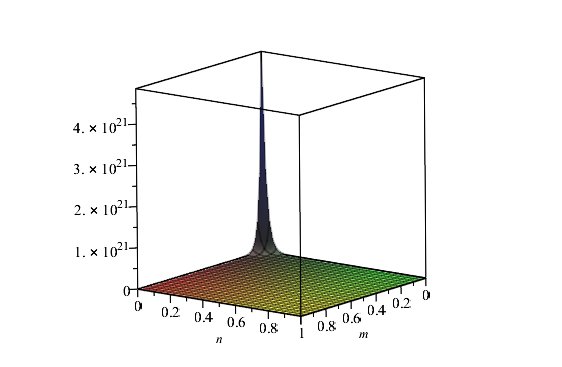
\begin{eqnarray*} F(MDN2[m,n])&=&\prod _{uv\in E(MDN2[m,n])}[du^{2} +dv^{2} ] \\ &=&\prod _{uv\in E_{1} (MDN2[m,n])}[du^{2} +dv^{2} ] \\ &&\times \prod _{uv\in E_{2} (MDN2[m,n])}[du^{2} +dv^{2} ]\\ &&\times \prod _{uv\in E_{3} (MDN2[m,n])}[du^{2} +dv^{2} ]\\ &&\times \prod _{uv\in E_{4} (MDN2[m,n])}[du^{2} +dv^{2} \\ &&\times \; \; \prod _{uv\in E_{5} (MDN2[m,n])}[du^{2} +dv^{2} ] \\ &&\times \prod _{uv\in E_{6} (MDN2[m,n])}[du^{2} +dv^{2} ] \\ &&\times\prod _{uv\in E_{7} (MDN2[m,n])}[du^{2} +dv^{2} ] \\ &&\times \prod _{uv\in E_{8} (MDN2[m,n])}[du^{2} +dv^{2} ]\\ &&\times \prod _{uv\in E_{9} (MDN2[m,n])}[du^{2} +dv^{2} ]\\ &&\times \prod _{uv\in E_{10} (MDN2[m,n])}[du^{2} +dv^{2} ]\\ && \times \prod _{uv\in E_{11} (MDN2[m,n])}[du^{2} +dv^{2} ]\\ &=& 45^{\left|E_{1} (MDN2[m,n])\right|} \times 34^{\left|E_{2} (MDN2[m,n])\right|} \times 61^{\left|E_{3} (MDN2[m,n])\right|}\\ &\times& 50^{\left|E_{4} (MDN2[m,n])\right|} \times 100^{\left|E_{5} (MDN2[m,n])\right|} \\ &\times& 89^{\left|E_{6} (MDN2[m,n])\right|} \times \; 74^{\left|E_{7} (MDN2[m,n])\right|} \times 98^{\left|E_{8} (MDN2[m,n])\right|}\\ &\times& 85^{\left|E_{9} (MDN2[m,n])\right|} \times 113^{\left|E_{10} (MDN2[m,n])\right|} \\ &\times& 128^{\left|E_{11} (MDN2[m,n])\right|}\\ &=& 45^{4} \times 34^{8} \times 61^{8} \times 50^{2(m+n-6)} \\ &\times& 100^{4} \times 89^{2(m+n-4)} \times 74^{4(m+n-6)} \times 98^{2(m+n-8)} \times 85^{8} \\ &\times& 113^{6(m+n-6)} \times 128^{(8mn-24(m+n)+72)} \end{eqnarray*}
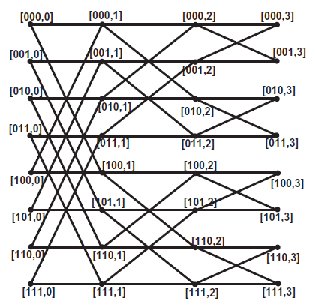
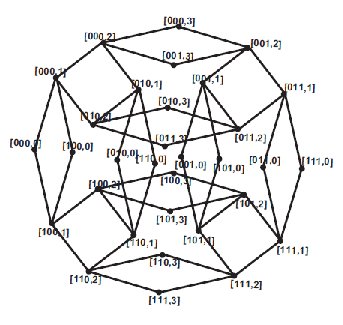
Let \(G=BF(r)\) be the butterfly network. From figure 12, we see that the graph has \(2r(r+1)\) number of vertices and \(r2r+1\) number of edges. The edge partition of graph \(G\) is shown in table 3.
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,4)\) | \(2^{r+2}\) |
| \((4,4)\) | \(2^{r+1}(r-2)\) |
Theorem 4.1. Let \(BF(r)\) is butterfly network then the Forgotten Polynomial and Forgotten Index of \(BF(r)\) are
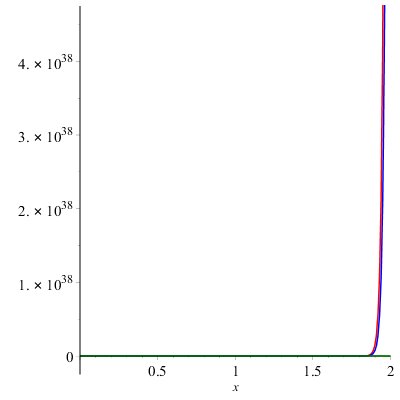
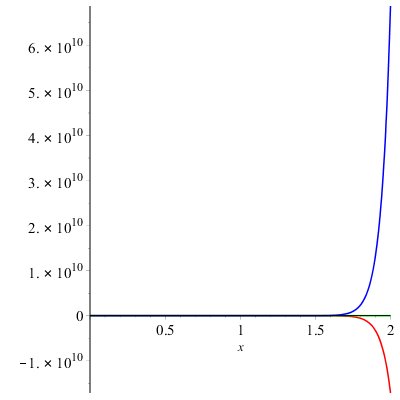
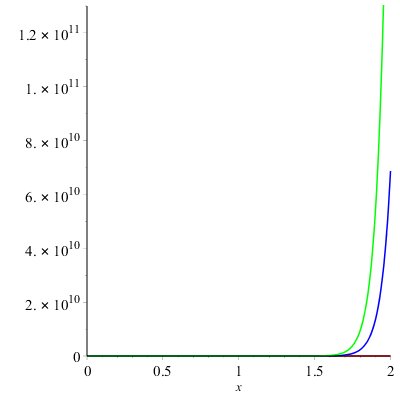
Proof. From the definition of forgotten polynomial we have \begin{eqnarray*} F(BF(r),x)&=&\sum _{uv\in E(BF(r))}x^{[du^{2} \; +dv^{2} ]} \\ &=&\sum _{uv\in E_{1} (BF(r))}x^{[du^{2} \; +dv^{2} ]} +\sum _{uv\in E_{2} (BF(r))}x^{[du^{2} \; +dv^{2} ]} \\ &=& \left|E_{1} (BF(r))\right|x^{20} +\left|E_{2} (BF(r))\right|x^{32} \\ &=& 2^{r+2} x^{20} +2^{r+1} (r-2)x^{32} \end{eqnarray*}
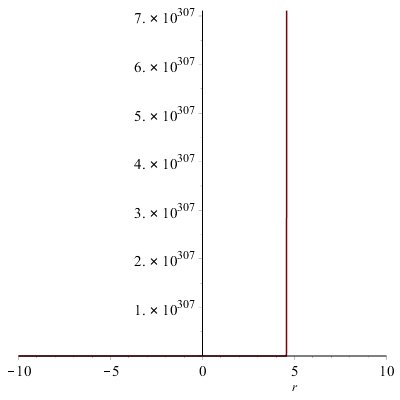
From the definition of forgotten index we have \begin{eqnarray*} F(BF(r))&=&\prod _{uv\in E(BF(r))}[du^{2} +dv^{2} ] \\ &=& \prod _{uv\in E_{1} (BF(r))}[du^{2} +dv^{2} ] \; \times \prod _{uv\in E_{2} (BF(r))}[du^{2} +dv^{2} ]\\ &=& 20^{\left|E_{1} (BF(r))\right|} \times 32^{\left|E_{2} (BF(r))\right|} \\ &=& 20^{2^{r+2} } \; \times 32^{2^{r+1} (r-2)} \end{eqnarray*}
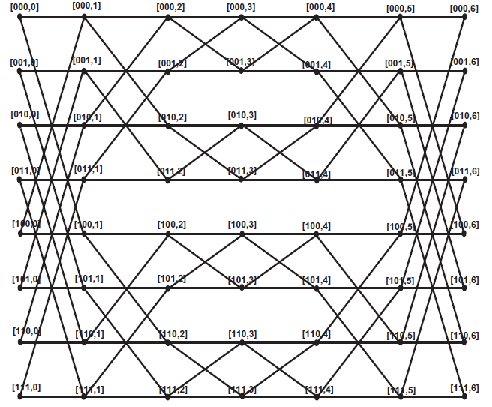
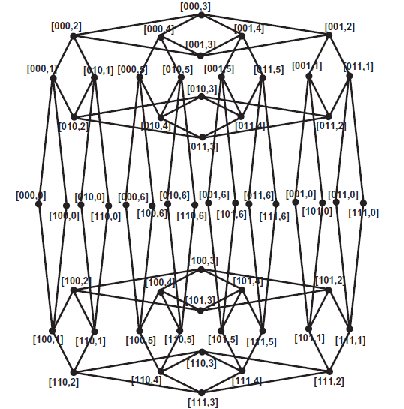
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,4)\) | \(2^{r+2}\) |
| \((4,4)\) | \(2^{r+2}(r-1)\) |
Theorem 5.1. Let \(B_{(r)}\) is Benes network then the Forgotten Polynomial $$F(B_{(r)} ,x)= 2^{r+2} x^{20} +2^{r+2} (r-1)x^{32} $$ and Forgotten Index of \(B_{(r)}\) are $$F(B_{(r)} )= 20^{2^{r+2} } \; \times 32^{2^{r+2} (r-1)} $$
Proof.
From the definition of forgotten polynomial we have
\begin{eqnarray*}
F(B_{(r)} ,x)&=&\sum _{uv\in E(B_{(r)} )}x^{[du^{2} \; +dv^{2} ]} \\
&=&\sum _{uv\in E_{1} (B_{(r)} )}x^{[du^{2} \; +dv^{2} ]} +\sum _{uv\in E_{2} (B_{(r)} )}x^{[du^{2} \; +dv^{2} ]} \\
&=&\left|E_{1} (B_{(r)} )\right|x^{20} +\left|E_{2} (B_{(r)} )\right|x^{32} \\
&=& 2^{r+2} x^{20} +2^{r+2} (r-1)x^{32}
\end{eqnarray*}
From the definition of forgotten index we have \begin{eqnarray*} F(B_{(r)})&=&\prod\limits_{uv\in E(B_{(r)} )}[du^{2} +dv^{2} ] \\ &=& \prod\limits _{uv\in E_{1} (B_{(r)} )}[du^{2} +dv^{2} ] \times \prod\limits _{uv\in E_{2} (B_{(r)} )}[du^{2} +dv^{2} ] \\ &=& 20^{\left|E_{1} (B_{(r)} )\right|} \times 32^{\left|E_{2} (B_{(r)} )\right|} \\ &=& 20^{2^{r+2}} \times 32^{2^{r+2} (r-1)} \end{eqnarray*}