On the entire Zagreb indices of the line graph and line cut-vertex graph of the subdivision graph

1. Introduction

Throughout this paper, only the finite, undirected, and simple graphs will be considered. Let \(G\) be such a graph with vertex set \(V(G)=\{v_1,v_2,\ldots,v_n\}\) and edge set \(E(G)\), where \(|V(G)|=n\) and \(|E(G)|=m\). These two basic parameters \(n\) and \(m\) are called the \(order\) and \(size\) of \(G\), respectively. The edge connecting the vertices \(u\) and \(v\) will be denoted by \(uv\). The \(degree\) of a vertex \(v\), written \(d_{G}(v)\), is the number of edges of \(G\) incident with \(v\), each loop counting as two edges.

Among the oldest and most studied topological indices, there are two classical vertex-degree based topological indices – the first Zagreb index and second Zagreb index. These two indices first appeared in [1], and were elaborated in [2]. The main properties of \(M_1(G)\) and \(M_2(G)\) were summarized in [3,4]. The first Zagreb index \(M_1(G)\) and the second Zagreb index \(M_2(G)\) of a graph \(G\) are defined, respectively, as

In fact, one can rewrite the first Zagreb index as During the past decades, numerous results concerning Zagreb indices have been put forward [5,6,7,8,9], for historical details, see [3].

In 2008, bearing in mind expression (3), Došlic put forward the first Zagreb coindex, defined as [10]

In view of expression (4), the second Zagreb coindex is defined analogously as [10] In expressions (4) and (5), it is assumed that \(u \neq v\).

Furtula and Gutman [11] introduced the forgotten index of \(G\), written \(F(G)\), as the sum of cubes of vertex degrees as follows;

\begin{equation*} F(G)=\displaystyle \sum_{v \in V(G)} d_{G} (v)^3=\displaystyle \sum_{e=uv \in E(G)} \left[d_{G}(u)^{2}+d_{G}(v)^{2}\right]. \end{equation*} Milicevic et al., [12] introduced the first and second reformulated Zagreb indices of a graph \(G\) as edge counterpart of the first and second Zagreb indices, respectively, as follows; \begin{equation*} EM_{1}(G)=\displaystyle \sum_{e \sim f} \left[d_{G}(e)+d_{G}(f)\right]=\displaystyle \sum_{e \in E(G)} d_{G}(e)^{2}, \end{equation*} \begin{equation*} EM_{2}(G)=\displaystyle \sum_{e \sim f} d_{G}(e)d_{G}(f), \end{equation*} where \(d_{G}(e)=d_{G}(u)+d_{G}(v)-2\) for the edge \(e=uv\) and \(e \sim f\) means that the edges \(e\) and \(f\) are incident.

Alwardi et al., [13] introduced the first and second entire Zagreb indices of a graph \(G\) as follows;

\begin{equation*} M_{1}^{\varepsilon}(G)=\displaystyle \sum_{x \in V(G) \cup E(G)} (d_{G}(x))^{2}, \end{equation*} \begin{equation*} M_{2}^{\varepsilon}(G)=\displaystyle \sum_{\{x,y\}\in B(G)} d_{G}(x)d_{G}(y), \end{equation*} where \(B(G)\) denotes the set of all 2-element subsets \(\{x,y\}\) such that \(\{x,y\} \subseteq V(G) \cup E(G)\) and members of \(\{x,y\}\) are adjacent or incident to each other.

The subdivision graph of a graph \(G\), written \(S(G)\), is the graph obtained from \(G\) by replacing each of its edges by a path of length 2, or equivalently by inserting an additional vertex into each edge of \(G\). The friendship graph, written \(F_{n}\), \(n\geq 2\), is a planar undirected graph with \(2n+1\) vertices and \(3n\) edges. The friendship graph can be constructed by joining \(n\) copies of the cycle graph \(C_3\) with a vertex in common.

There are many graph operators (or graph valued functions) with which one can construct a new graph from a given graph, such as the line graphs, line cut-vertex graphs; total graphs; and their generalizations. The line graph of a graph \(G\), written \(L(G)\), is the graph whose vertices are the edges of \(G\), with two vertices of \(L(G)\) adjacent whenever the corresponding edges of \(G\) have a vertex in common.

In [14], the Zagreb indices and coindices of the line graphs of the subdivision graphs were studied.

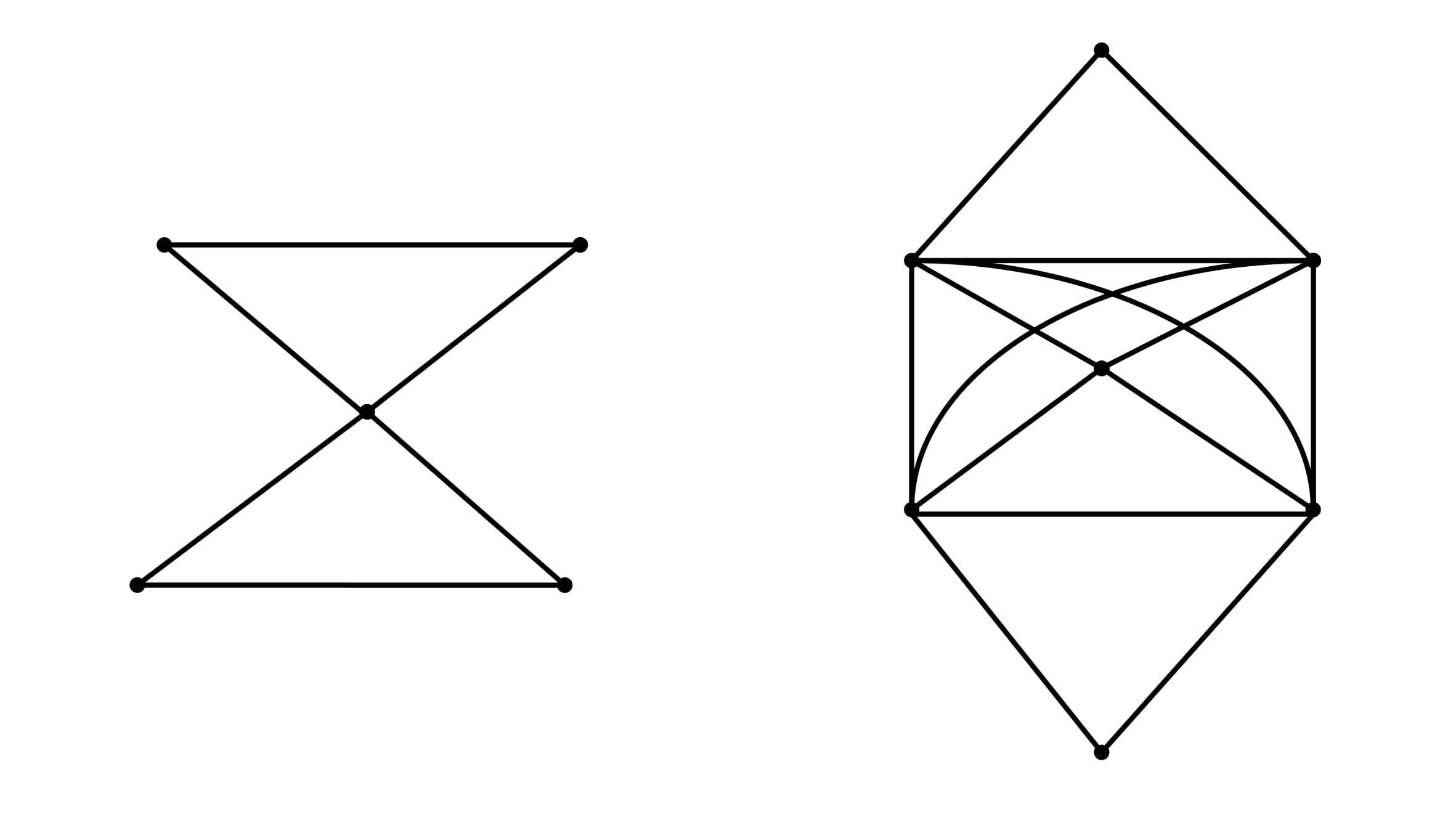
The author in [15] gave the following definition. The line cut-vertex graph of \(G\), written \(L_{c}(G)\), is the graph whose vertices are the edges and cut-vertices of \(G\), with two vertices of \(L_{c}(G)\) adjacent whenever the corresponding edges of \(G\) have a vertex in common; or one corresponds to an edge \(e_i\) of \(G\) and the other corresponds to a cut-vertex \(c_j\) of \(G\) such that \(e_i\) is incident with \(c_j\). Clearly, \(L(G) \subseteq L_{c}(G)\), where \(\subseteq\) is the subgraph notation. Figure 1 shows an example of a graph \(G\) and its line cut-vertex graph \(L_{c}(G)\).

In this paper we study the line graph and line cut-vertex graph of the subdivision graph of the friendship graph; and calculate the entire Zagreb indices of the graphs \(L(S(F_{n}))\) and \(L_{c}(S(F_{n}))\). Notations and definitions not introduced here can be found in [16].

2. Entire Zagreb indices of the line graph of the subdivision graph of the friendship graph \(F_n, n \geq 2\)

In this section we calculate the entire Zagreb indices of the line graph of the subdivision graph of the friendship graph.

Theorem 1. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \(M_1(G)=8n^{3}+16n\) and \(M_{2}(G)=8n^{4}-4n^{3}+8n^{2}+12n\).

Proof. The subdivision graph \(S(F_{n})\) contains \(5n+1\) vertices and \(6n\) edges, so that the line graph of \(S(F_{n})\) contains \(6n\) vertices, out of which \(2n\) vertices of are of degree \(2n\) and the remaining \(4n\) vertices are of degree \(2\). Thus \(M_1(G)=8n^{3}+16n\).

Now, in order to find \(M_2(G)\), we first find the size of \(L(S(F_{n}))\). Every \(L(S(F_{n}))\) contains exactly one copy of \(K_{2n}\) and \(5n\) edges. Thus the size of \(L(S(F_{n}))\) is \(|E(L(S(F_{n})|=2n^{2}+4n\). Out of these edges, \(3n\) edges whose end vertices are of degree 2; \(2n\) edges whose end vertices have degree \(2\) and \(2n\); and the remaining \(n(2n-1)\) edges whose end vertices have degree \(2n\). Thus \(M_2(G)=8n^{4}-4n^{3}+8n^{2}+12n\).

Gutman et al., in [8] established a complete set of relations between first and second Zagreb index and coindex of a graph as follows;

Theorem 2. Let \(G\) be a graph with \(n\) vertices and \(m\) edges. Then \begin{equation} \overline{M_{1}}(G)=2m(n-1)-M_1(G), \\ \overline{M_{2}}(G)=2m^2-\frac{1}{2} M_1(G)-M_2(G). \end{equation} We now give the expressions for the first and second Zagreb coindices of the line graph of the subdivision graph of the friendship graph using Theorem 2.

Theorem 3. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \(\overline{M_1}(G)=16n^3+44n^2-24n\).

Proof. The order and size of \(G\) are \(6n\) and \(2n^{2}+4n\), respectively. Then Theorem 1 and Theorem 2, give us the result.

Theorem 4. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \(\overline{M_2}(G)=32n^{3}+24n^{2}-20n\).

Proof. Theorem 1 and Theorem 2, give us the result.

We now find the forgotten index; and first and second reformulated Zagreb indices of the line graph of the subdivision graph of the friendship graph.

Proposition 1. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \(F(G)=16n^4+32n\).

Theorem 5. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \(EM_{1}(G)=32n^4-40n^3+24n^2+8n\).

Proof. The size of \(G\) is \(2n^2+4n\), out of which \(3n\) edges are of degree \(2\); \(2n\) edges are of degree \(2n\); and the remaining \(n(2n-1)\) edges are of degree \(4n-2\). Then \(EM_{1}(G)=32n^4-40n^3+24n^2+8n\).

Theorem 6. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \(EM_{2}(G)=\frac{1}{2}\left(108n^8-300n^7+128n^6+219n^5-179n^4-4n^3+36n^2-8n\right)\).

Proof. Let \(G\) be the line graph of the subdivision graph of the friendship graph. We consider the following four cases:

Case \(1\): There are \(2n\) pairs of edges with degree \(2\). Then the second reformulated Zagreb index is \(8n\).

Case \(2\): There are \(2n\) pairs of edges with degree \(2\) and \(2n\). Then the second reformulated Zagreb index is \(8n^2\).

Case \(3\): There are \(2n(n-1)\) pairs of edges with degree \(2n\) and \(4n-2\). Then the second reformulated Zagreb index is \(4n^2(2n-1)(4n-2)\).

Case \(4\): There are \(\frac{(2n^2-n)(2n^2-n-1)(2n^2-n-2)}{2}\) pairs of edges with degree \(4n-2\). Then the second reformulated Zagreb index is \((4n-2)^2\left(\frac{(2n^2-n)(2n^2-n-1)(2n^2-n-2)}{2}\right)\).

From all the cases mentioned above, we get

\(EM_{2}(G)=\frac{1}{2}\left(108n^8-300n^7+128n^6+219n^5-179n^4-4n^3+36n^2-8n\right)\).

Ghalavand and Ashrafi in [17] established a complete set of relations between entire Zagreb indices with the Zagreb and reformulated Zagreb indices of graphs as follows;

Theorem 7. Let \(G\) be a graph with \(n\) vertices and \(m\) edges. Then \begin{equation*} \begin{split} M_{1}^{\varepsilon}(G)&=M_{1}(G)+EM_{1}(G),\\ M_{2}^{\varepsilon}(G)&=3M_{2}(G)+EM_{2}(G)+F(G)-2M_{1}(G). \end{split} \end{equation*} We now give the expressions for the entire Zagreb indices of the line graph of the subdivision graph of the friendship graph.

Theorem 8. Let \(G\) be the line graph of the subdivision graph of the friendship graph. Then \begin{equation*} \begin{split} M_{1}^{\varepsilon}(G)&=32n^4-32n^3+24n^2+24n,\\ M_{2}^{\varepsilon}(G)&=\frac{1}{2}\left(108n^8-300n^7+128n^6+219n^5-99n^4-60n^3+84n^2+64n\right). \end{split} \end{equation*}

Proof. Theorem 1, Proposition 1, and Theorems 5,6,7, give us the results.

3. Entire Zagreb indices of the line cut-vertex graph of the subdivision graph of the friendship graph

In this section we calculate the entire Zagreb indices of the line cut-vertex graph of the subdivision graph of the friendship graph.

Theorem 9. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \(M_1(G)=8n^{3}+12n^{2}+18n\) and \(M_{2}(G)=8n^{4}+12n^{3}+10n^{2}+15n\).

Proof. The line cut-vertex graph of \(S(F_{n})\) contains \(6n+1\) vertices, out of which \(2n\) vertices of are of degree \(2n+1\); \(4n\) vertices are of degree \(2\); and the remaining single vertex is of degree \(2n\). Thus \(M_1(G)=8n^{3}+12n^{2}+18n\).

Every \(L_{c}(S(F_{n}))\) contains exactly one copy of \(K_{2n+1}\) and \(5n\) edges. Thus the size of \((S(L_{c}(F_{n}))\) is \(|E(L_{c}(S(F_{n})| = \frac{4n^2+12n}{2}\). Out of these edges, \(3n\) edges whose end vertices are of degree 2; \(2n\) edges whose end vertices have degree \(2\) and \(2n+1\); \(n(2n-1)\) edges whose end vertices have degree \(2n+1\); and the remaining \(2n\) edges whose vertices have degree \(2n\) and \(2n+1\). Thus \(M_2(G)=8n^{4}+12n^{3}+10n^{2}+15n\).

We now give the expressions for the first and second Zagreb coindices of the line cut-vertex graph of the subdivision graph of the friendship graph using Theorem 2.

Theorem 10. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \(\overline{M_1}(G)=16n^3+60n^2-18n\).

Proof. The order and size of \(G\) are \(6n+1\) and \(2n^{2}+6n\), respectively. Then Theorem 9 and Theorem 2, give us the result.

Theorem 11. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \(\overline{M_2}(G)=32n^{3}+56n^{2}-24n\).

Proof. Theorem 9 and Theorem 2, give us the result.

We now find the forgotten index; and first and second reformulated Zagreb indices of the line cut-vertex graph of the subdivision graph of the friendship graph.

Proposition 2. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \(F(G)=16n^4+32n^3+12n^2+34n\).

Theorem 12. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \(EM_{1}(G)=32n^4+24n^3-8n^2+16n\).

Proof. The size of \(G\) is \(\frac{4n^2+12n}{2}\), out of which \(3n\) edges are of degree \(2\); \(2n\) edges are of degree \(2n+1\); \(n(2n-1)\) edges are of degree \(4n\); and the remaining \(2n\) edges are of degree \(4n-1\). Then \(EM_{1}(G)=32n^4+24n^3-8n^2+16n\).

Theorem 13. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \(EM_{2}(G)=64n^8-96n^7-48n^6+88n^5+104n^4-48n^3-12n^2+10n\).

Proof. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. We consider the following six cases:

Case \(1\): There are \(2n\) pairs of edges with degree \(2\). Then the second reformulated Zagreb index is \(8n\).

Case \(2\): There are \(2n\) pairs of edges with degree \(2\) and \(2n+1\). Then the second reformulated Zagreb index is \(8n^2+4n\).

Case \(3\): There are \(2n\) pairs of edges with degree \(2n+1\) and \(4n-1\). Then the second reformulated Zagreb index is \(16n^3+4n^2-2n\).

Case \(4\): There are \(4n^2-2n\) pairs of edges with degree \(2n+1\) and \(4n\). Then the second reformulated Zagreb index is \(32n^4-8n^2\).

Case \(5\): There are \(\frac{(2n^2-n)(2n^2-n-1)(2n^2-n-2)}{2}\) pairs of edges with degree \(4n\). Then the second reformulated Zagreb index is \((4n)^2\left(\frac{(2n^2-n)(2n^2-n-1)(2n^2-n-2)}{2}\right)\).

Case \(6\): There are \((4n^2-2n)\) pairs of edges with degree \(4n-1\) and \(4n\). Then the second reformulated Zagreb index is \(64n^4-48n^3+8n^2\).

From all the cases mentioned above, we get

\(EM_{2}(G)=64n^8-96n^7-48n^6+88n^5+104n^4-48n^3-12n^2+10n\).

We now give the expressions for the entire Zagreb indices of the line cut-vertex graph of the subdivision graph of the friendship graph.

Theorem 14. Let \(G\) be the line cut-vertex graph of the subdivision graph of the friendship graph. Then \begin{equation*} \begin{split} M_{1}^{\varepsilon}(G)&=32n^4+32n^3+4n^2+34n,\\ M_{2}^{\varepsilon}(G)&=64n^8-96n^7-48n^6+88n^5+144n^4+4n^3+6n^2+53n. \end{split} \end{equation*}

Proof. Theorem 9, Proposition 2, and Theorems 8,12,13, give us the results.

4. Conclusion

In this paper we have investigated the entire Zagreb indices of the line graph and line cut-vertex graph of the subdivision graph of the friendship graph. However, to determine the Zagreb indices and coindices of some other graph operators still remain open and challenging problem for researchers.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of interest

The authors declare no conflict of interest.