A q-rung orthopair fuzzy matrix (q-ROFM), an extension of the Pythagorean fuzzy matrix (PFM) and intuitionistic fuzzy matrix (IFM), is very helpful in representing vague information that occurs in real-world circumstances. In this paper we define some algebraic operations, such as max-min, min-max, complement, algebraic sum, algebraic product, scalar multiplication \((nA)\), and exponentiation \((A^n)\). We also investigate the algebraic properties of these operations. Furthermore, we define two operators, namely the necessity and possibility to convert q-ROFMs into an ordinary fuzzy matrix, and discuss some of their basic algebraic properties. Finally, we define a new operation(@) on q-ROFMs and discuss distributive laws in the case where the operations of \(\oplus_{q}, \otimes_{q}, \wedge_{q}\) and \(\vee_{q}\) are combined each other.
The concept of an intuitionistic fuzzy matrix (IFM) was introduced by Khan et al. [1] and Im et al. [2] to generalize the concept of Thomason’s fuzzy matrix [3]. Each element in an IFM is expressed by an ordered pair \(\left\langle \mu_{a_{ij}},\nu_{a_{ij}}\right\rangle\) with \(\mu_{a_{ij}},\nu_{a_{ij}}\in [0,1]\) and \(0\leq \mu_{a_{ij}}+\nu_{a_{ij}}\leq 1\). Since the IFS was proposed, it has received a lot of attention in many fields, such as pattern recognition, medical diagnosis, and so on. But if the sum of the membership degree and the nonmembership degree is greater than 1, the IFM is no longer applicable. Khan and Pal [4] defined some basic operations and relations of IFMs including maxmin, minmax, complement, algebraic sum, algebraic product etc. and proved equality between IFMs. After the introduction of IFM theory, many researchers attempted the important role in IFM theory [5,6,7,8,9,10,11,12,13,14].
Yager [15] introduced the concept of a Pythagorean fuzzy set (PFS) and developed some aggregation operations for PFS. Zhang and Xu [16] studied various binary operations over PFS and also proposed a decision making algorithm based on PFS. Recently, Yager [17] proposed the concept of the q-ROFS, in which MD u and NMD satisfy \(\mu^q+\nu^q\leq 1 (q\geq 1)\). We can see that the IFS and PFS are special cases of q-ROFS. As q-rung increases, the range of processing fuzzy information increases. In recent years, the topic of information aggregation has attracted a lot of attention and is one of the key research issues in the problems of MAGDM. As far as q-ROFS is concerned, different aggregation operators have been introduced and applied, such as q-ROFWA and q-ROFWG operator [18]. After the introduction of q-ROFS theory, many researchers attempted the important role in PFS and q-ROFS theory [19,20,21,22,23,24,25].
Using the theory of PFS ans q-ROFS, Silambarasan and Sriram [26] defined the Pythagorean fuzzy matrix (PFM) theory and its algebraic operations. Each element in an PFM is expressed by an ordered pair \(\left\langle \mu_{a_{ij}},\nu_{a_{ij}}\right\rangle\) with \(\mu_{a_{ij}},\nu_{a_{ij}}\in [0,1]\) and \(0\leq \mu^2_{a_{ij}}+\nu^2_{a_{ij}}\leq 1\). Also,they constructed \(nA\) and \(A^n\) of a Pythagorean fuzzy matrix \(A\) and using these operations. Further, they defined the commutative monoid on Pythagorean fuzzy matrices and proved that the set of all PFMs forms a commutative monoid [27]. After the introduction of PFM theory, many researchers worked in PFM and Fermatean fuzzy matrix theory [28]. Since the PFM was brought up, it has been widely applied in FM operations on q-ROFMs and prove their desirable properties. In Section 5, we define necessity and possibility on q-ROFMs and proved some algebraic properties of these operations. In Section 6, we define a new operation(@) on q-ROFMs and investigated their algebraic properties. We write the conclusion of the paper in the last section.
Definition 1.[1] An intuitionistic fuzzy matrix (IFM) is a pair \(A=\left[\left\langle \mu_{a_{ij}}, \nu_{a_{ij}}\right\rangle\right]\) of a non negative real numbers \(\mu_{a_{ij}}, \nu_{a_{ij}}\in [0,1]\) satisfying \(0\leq \mu_{a_{ij}}+\nu_{a_{ij}}\leq 1\) for all \(i,j.\)
Definition 2.[26] A Pythagorean fuzzy matrix (PFM) is a pair \(A=\left[\left\langle \mu_{a_{ij}}, \nu_{a_{ij}}\right\rangle\right]\) of non negative real numbers \(\mu_{a_{ij}}, \nu_{a_{ij}}\in [0,1]\) satisfying the condition \(0\leq\mu^2_{a_{ij}}+\nu^2_{a_{ij}}\leq 1\), for all \(i,j\). Where \(\mu_{a_{ij}}\in[0,1]\) is called the degree of membership and \(\nu_{a_{ij}}\in[0,1]\) is called the degree of non-membership.
Definition 3. A q-rung orthopair fuzzy matrix (q-ROFM) is a pair \(A=\left[\left\langle \mu_{a_{ij}}, \nu_{a_{ij}}\right\rangle\right]\) of non negative real numbers \(\mu_{a_{ij}}, \nu_{a_{ij}}\in [0,1]\) satisfying the condition \(0\leq\mu^q_{a_{ij}}+\nu^q_{a_{ij}}\leq 1 (q\geq 1)\), for all \(i,j\). Where \(\mu_{a_{ij}}\in[0,1]\) is called the degree of membership and \(\nu_{a_{ij}}\in[0,1]\) is called the degree of non-membership.
For understanding the q-ROFM better, we give an instance to illuminate the understandability of the q-ROFM: We can definitely get \(0.9+0.6 > 1\), and, therefore, it does not follow the condition of intuitionistic fuzzy matrices. Also, we can get \((0.9)^2+(0.6)^2 =0.81 + 0.36 = 1.17 > 1\), which does not obey the constraint condition of Pythagorean fuzzy matrices. However, we can get \((0.9)^q+(0.6)^q \leq 1 ~(q\geq 1)\), which is good enough to apply the q-ROFM to control it.Theorem 1. The q-ROFMs is larger than the set of PFMs and IFMs.
Proof.
Any intuitionistic fuzzy matrix \((\mu_{a_{ij}},\nu_{a_{ij}})\) that is an IFM is also a PFM and a q-ROFM. For any two fuzzy matrices \(A, B\in [0,1]\), we get \(\mu^q_{a_{ij}}\leq \mu^2_{a_{ij}}\leq \mu_{a_{ij}}\) and \(\nu^q_{a_{ij}}\leq \nu^2_{a_{ij}}\leq \nu_{a_{ij}}\). Thus \(\mu_{a_{ij}}+\nu_{a_{ij}}\leq 1 \Rightarrow \mu^2_{a_{ij}}+\nu^2_{a_{ij}}\leq 1 \Rightarrow \mu^q_{a_{ij}}+\nu^q_{a_{ij}}\leq 1.\) Consider a point \((0.9,0.6)\), we see that \((0.9)^q+(0.6)^q\leq 1, (q \geq 1)\) thus this is an q-ROFM. Since \((0.9)^2+(0.6)^2 =0.81+0.36=1.17\geq 1\) and \(0.9+0.6\geq 1\), therefore \((0.9,0.6)\) is neither a PFM nor an IFM.
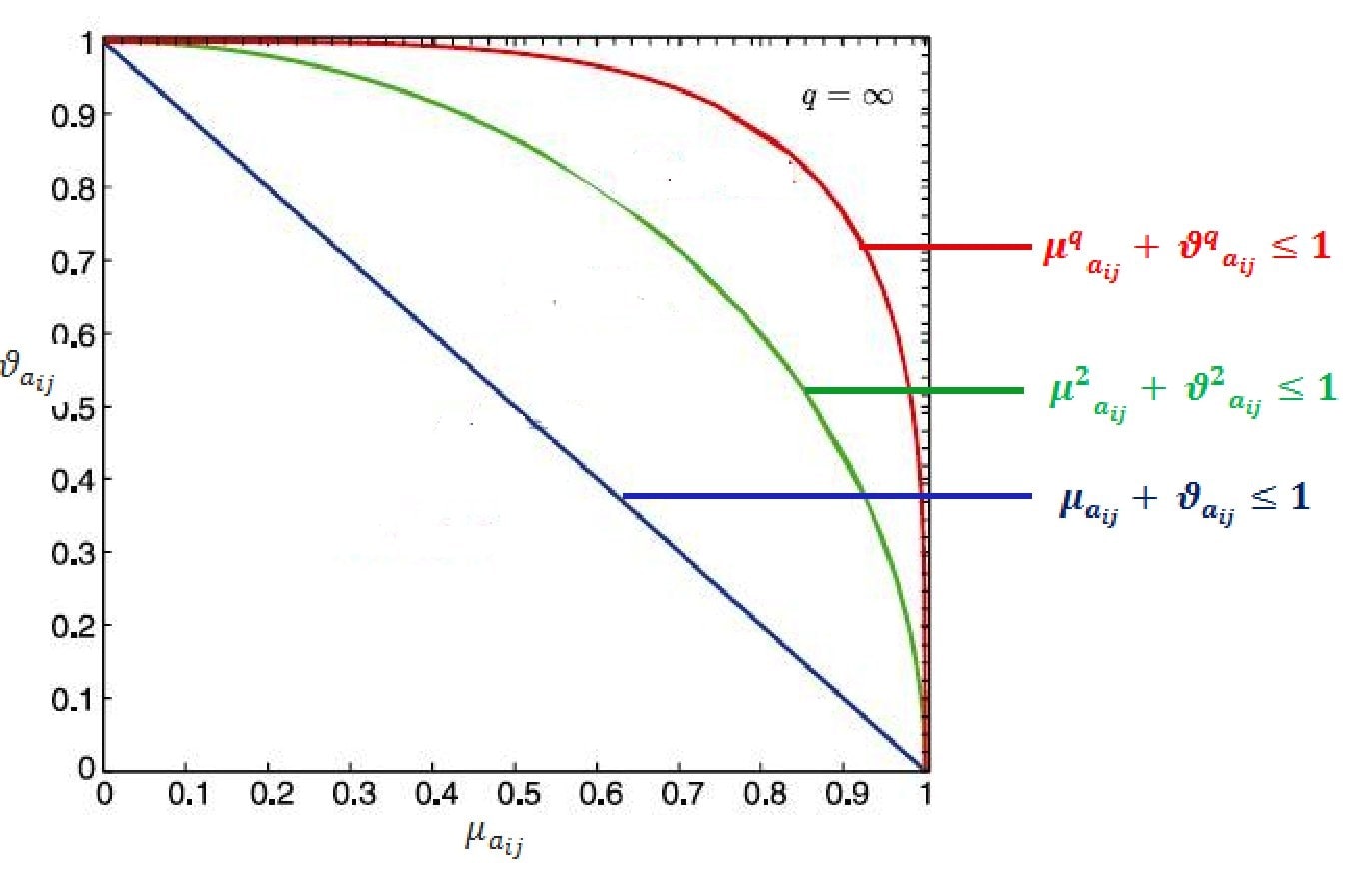
This development can be evidently recognized in Figure 1. Here we notice that IFMs are all points beneath the line \(\mu_{a_{ij}}+\nu_{a_{ij}}\leq 1,\) the PFMs are all points with \(\mu^2_{a_{ij}}+\nu^2_{a_{ij}}\leq 1,\) and the q-ROFMs are all points with \(\mu^q_{a_{ij}}+\nu^q_{a_{ij}}\leq 1\). We see then that the q-ROFMs enable for the presentation of a bigger body of nonstandard membership function then IFMs and PFMs. Here \(Q_{m\times n}\) denote the set of all the q-ROFMs.
Definition 4. Let \(A=\left[\left\langle \mu_{a_{ij}},\nu_{a_{ij}}\right\rangle\right]\) and \(B=\left[\left\langle \mu_{b_{ij}},\nu_{b_{ij}}\right\rangle\right]\) be two q-ROFMs of the same size. Then
Definition 5. Let \(A=\left[\left\langle \mu_{a_{ij}},\nu_{a_{ij}}\right\rangle\right]\) and \(B=\left[\left\langle \mu_{b_{ij}},\nu_{b_{ij}}\right\rangle\right]\) be two q-ROFMs of the same size. Then
Theorem 2. For \(A, B\in Q_{m\times n}\), we have
Proof.
Theorem 3. For \(A, B\in Q_{m\times n}\), we have
Proof. Here we prove (i), (iii) and (vi). The remaining are similar.
Theorem 4. For \(A, B\in Q_{m\times n}\), we have
Proof. Here we prove (i), (iii) and (iv). The remaining are similar.
Theorem 5. For \(A, B, C\in Q_{m\times n}\), we have
Proof. Here we prove(i), (iii) and (v). The remaining can be proved analogously.
(i)
\begin{align*} (A\vee_{q} B)\wedge_{q} C &=\left[\left\langle \min\left\{\max\left\{\mu_{a_{ij}},\mu_{b_{ij}}\right\},\mu_{c_{ij}}\right\},\max\left\{\min\left\{\nu_{a_{ij}},\nu_{b_{ij}}\right\}\nu_{c_{ij}}\right\}\right\rangle\right]\\ &=\left[\left\langle \max\left\{\min\left\{\mu_{a_{ij}},\mu_{b_{ij}}\right\},\min\left\{\mu_{a_{ij}},\mu_{c_{ij}}\right\}\right\},\min\left\{\max\left\{\nu_{a_{ij}},\nu_{b_{ij}}\right\},\max\left\{\nu_{b_{ij}},\nu_{c_{ij}}\right\}\right\}\right\rangle\right]\\ &=\left[\left\langle\left\{\min\left\{\mu_{a_{ij}},\mu_{c_{ij}}\right\},\max\left\{\nu_{a_{ij}},\nu_{c_{ij}}\right\}\right\}\bigvee \left\{\min\left\{\nu_{b_{ij}},\nu_{c_{ij}}\right\},\max\left\{\nu_{b_{ij}},\nu_{c_{ij}}\right\}\right\}\right\rangle\right]\\ &=(A\wedge_{q} C)\vee_{q} (B\wedge_{q} C).\end{align*} Hence, \((A\vee_{q} B)\wedge_{q} C=(A\wedge_{q} C)\vee_{q} (B\wedge_{q} C).\)(iii)
\begin{align*} (A\vee_{q} B)\oplus_{q} C&=\left(\max\left\{\mu_{a_{ij}},\mu_{b_{ij}}\right\},\min\left\{\nu_{a_{ij}},\nu_{b_{ij}}\right\}\right)\oplus \left(\mu_{c_{ij}}, \nu_{c_{ij}} \right)\\ &=\left[\left\langle \left(\max\left\{\mu_{a_{ij}}^q,\mu_{b_{ij}}^q\right\}+\mu_{c_{ij}}^q-\max\left\{\mu_{a_{ij}}^q,\mu_{b_{ij}}^q\right\}\mu_{c_{ij}}^q\right)^{1/q} ,\min\left\{\nu_{a_{ij}},\nu_{b_{ij}}\right\}\nu_{c_{ij}}\right\rangle\right]\\ &=\left[\left\langle \left((1-\mu_{c_{ij}}^q)\max\left\{\mu_{a_{ij}}^q,\mu_{b_{ij}}^q\right\}+\mu_{c_{ij}}^q\right)^{1/q},\min\left\{\nu_{a_{ij}}\nu_{c_{ij}},\nu_{b_{ij}}\nu_{c_{ij}}\right\}\right\rangle\right].\end{align*} \begin{align*}(A\oplus_{q} C)\vee_{q} (B\oplus_{q} C)&=\left[\left\langle \max\left\{\left(\mu_{a_{ij}}^q+\mu_{c_{ij}}^q-\mu_{a_{ij}}^q\mu_{c_{ij}}^q\right)^{1/q},\left(\mu_{b_{ij}}^q+\mu_{c_{ij}}^q-\mu_{b_{ij}}^q\mu_{c_{ij}}^q\right)^{1/q}\right\},\min\left\{\nu_{a_{ij}}\nu_{c_{ij}},\nu_{b_{ij}}\nu_{c_{ij}}\right\}\right\rangle\right]\\ &=\left[\left\langle \max\left\{\left((1-\mu_{c_{ij}}^q)\mu_{a_{ij}}^q+\mu_{c_{ij}}^q\right)^{1/q},\left((1-\mu_{c_{ij}}^q)\mu_{b_{ij}}^q+\mu_{c_{ij}}^q\right)^{1/q}\right\},\min\left\{\nu_{a_{ij}}\nu_{c_{ij}},\nu_{b_{ij}}\nu_{c_{ij}}\right\}\right\rangle\right]\\ &=\left[\left\langle \left((1-\mu_{c_{ij}}^q)\max\left\{\mu_{a_{ij}}^q,\mu_{b_{ij}}^q\right\}+\mu_{c_{ij}}^q\right)^{1/q},\min\left\{\nu_{a_{ij}}\nu_{c_{ij}},\nu_{b_{ij}}\nu_{c_{ij}}\right\}\right\rangle\right]\\ &=(A\vee_{q} B)\oplus_{q}C.\end{align*} Hence, \((A\vee_{q} B)\oplus_{q} C=(A\oplus_{q} C)\vee_{q} (B\oplus_{q} C)\).(v)
\begin{align*} (A\vee_{q} B)\otimes_{q}C&=\left[\left\langle \max\left\{\mu_{a_{ij}},\mu_{b_{ij}}\right\}\mu_{c_{ij}},\left(\min\left\{\nu^q_{a_{ij}},\nu^q_{b_{ij}}\right\}+\nu^q_{c_{ij}}-\min\left\{\nu^q_{a_{ij}},\nu^q_{b_{ij}}\right\}\nu^q_{c_{ij}}\right)^{1/q}\right\rangle\right]\\ &=\left[\left\langle \max\left\{\mu_{a_{ij}},\mu_{b_{ij}}\right\}\mu_{c_{ij}},\left((1-\nu^q_{c_{ij}})\min\left\{\nu^q_{a_{ij}},\nu^q_{b_{ij}}\right\}+\nu^q_{c_{ij}}\right)^{1/q}\right\rangle\right].\end{align*} \begin{align*}(A\otimes_{q} C)\vee_{q} (B\otimes_{q} C) &=\left[\left\langle \max\left\{\mu_{a_{ij}}\mu_{c_{ij}},\mu_{b_{ij}}\mu_{c_{ij}}\right\},\min\left\{\left(\nu^q_{a_{ij}}+\nu^q_{c_{ij}}-\nu^q_{a_{ij}}\nu^q_{c_{ij}}\right)^{1/q},\left(\nu^q_{b_{ij}}+\nu^q_{c_{ij}}-\nu^q_{b_{ij}}\nu^q_{c_{ij}}\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle \max\left\{\mu_{a_{ij}}\mu_{c_{ij}},\mu_{b_{ij}}\mu_{c_{ij}}\right\},\min\left\{\left((1-\nu_{c_{ij}}^q)\nu_{a_{ij}}^q+\nu_{c_{ij}}^q\right)^{1/q},\left((1-\nu_{c_{ij}}^q)\nu_{b_{ij}}^q+\nu_{c_{ij}}^q\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle \max\left\{\mu_{a_{ij}},\mu_{b_{ij}}\right\}\mu_{c_{ij}},\left((1-\nu^q_{c_{ij}})\min\left\{\nu^q_{a_{ij}},\nu^q_{b_{ij}}\right\}+\nu^q_{c_{ij}}\right)^{1/q}\right\rangle\right]\\ &=(A\vee_{q} B)\otimes_{q} C.\end{align*} Hence, \((A\vee_{q} B)\otimes_{q} C=(A\otimes_{q} C)\vee_{q} (B\otimes_{q} C) \).Theorem 6. For any q-ROFM \(A\), we have
Proof.
Similarly, we can prove \(O\oplus_{q} A=A\).
Similarly, we can prove \(J\otimes_{q} A=A\).
Theorem 7. For any q-ROFM \(A\), we have
Proof.
Similarly, we can prove \(J\oplus_{q} A=J\).
Similarly, we can prove \(O\otimes_{q} A=O\).
Definition 6. For every q-ROFM \(A\), the necessity \((\Box)\) and possibility \((\Diamond)\) operators are defined as follows: \[\Box A=\left[\left\langle \mu_{a_{ij}},\left(1-\mu_{a_{ij}}^q\right)^{1/q}\right\rangle\right],\] \[\Diamond A=\left[\left\langle \left(1-\nu^q_{a_{ij}}\right)^{1/q},\nu_{a_{ij}}\right\rangle\right].\]
Theorem 8. For \(A, B\in Q_{m\times n}\), we have
Proof. (i) \begin{align*} \Box(A\oplus_{q} B)&=\left[\left\langle \left(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q\right)^{1/q},\left(1-(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q)\right)^{1/q}\right\rangle\right]\\ \Box A\oplus_{q} \Box B&=\left[\left\langle \left(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q\right)^{1/q},\left(1-\mu_{a_{ij}}^q\right)^{1/q} \left(1-\mu_{b_{ij}}^q\right)^{1/q}\right\rangle\right]\\ &=\left[\left\langle \left(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q\right)^{1/q},\left(1-(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q)\right)^{1/q}\right\rangle\right]. \end{align*} Hence, \(\Box(A\oplus_{q} B)=\Box A\oplus_{q} \Box B\).
(ii)
\begin{align*} \Diamond (A\oplus_{q} B)&=\left[\left\langle \left(1-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q},\nu_{a_{ij}}\nu_{b_{ij}}\right\rangle\right]\\ \Diamond A\oplus_{q} \Diamond B &=\left[\left\langle \left((1-\nu^q_{a_{ij}})+(1-\nu^q_{b_{ij}})-(1-\nu^q_{a_{ij}})(1-\nu^q_{b_{ij}})\right)^{1/q},\nu_{a_{ij}}\nu_{b_{ij}}\right\rangle\right] &=\left[\left\langle \left(1-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q},\nu_{a_{ij}}\nu_{b_{ij}}\right\rangle\right].\end{align*} Hence, \(\Diamond (A\oplus_{q} B)=\Diamond A\oplus_{q} \Diamond B\).Theorem 9. For \(A, B\in Q_{m\times n}\), we have
Proof.
Theorem 10. For \(A, B\in Q_{m\times n}\), we have
Proof.
Theorem 11. For \(A, B\in Q_{m\times n}\), we have
Proof.
Definition 7. Let \(A=\left[\left\langle \mu_{a_{ij}}, \nu_{a_{ij}}\right\rangle\right],\) and \(B=\left[\left\langle\mu_{b_{ij}}, \nu_{b_{ij}}\right\rangle\right]\) be any two q-ROFMs. The new operation of q-ROFM is defined by \[A@B=\left[\left\langle\left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\rangle\right].\]
Theorem 12. For any q-ROFM \(A\), we have \(A@A=A.\)
Proof. \begin{align*} A@A&=\left[\left\langle \left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{a_{ij}}}{2}\right)^{1/q},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{a_{ij}}}{2}\right)^{1/q}\right\rangle\right]\\ &=\left[\left\langle \left(\dfrac{2\mu^q_{a_{ij}}}{2}\right)^{1/q}, \left(\dfrac{2\nu^q_{a_{ij}}}{2}\right)^{1/q}\right\rangle\right]\\ &=\left[\left\langle \mu^q_{a_{ij}}, \nu^q_{a_{ij}}\right\rangle\right]\\ &=\left[\left\langle \mu_{a_{ij}}, \nu_{a_{ij}}\right\rangle\right]\\ &=A.\end{align*}
Theorem 13. For \(A, B\in Q_{m\times n}\), we have
Proof. (i) \begin{align*} (A\oplus_{P} B)\wedge_{q} (A\otimes_{q} B) &=\left[\left\langle \min\left\{ \left(\mu^q_{a_{ij}}+\mu^q_{b_{ij}}-\mu^q_{a_{ij}}\mu^q_{b_{ij}}\right)^{1/q}, \mu_{a_{ij}}\mu_{b_{ij}}\right\},\max\left\{ \nu_{a_{ij}}\nu_{b_{ij}},\left(\nu^q_{a_{ij}}+\nu^q_{b_{ij}}-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle \mu_{a_{ij}}\mu_{b_{ij}}, \left(\nu^q_{a_{ij}}+\nu^q_{b_{ij}}-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q}\right\rangle\right]\\ &=A\otimes_{q} B.\end{align*} Hence, \((A\oplus_{q} B)\wedge_{q} (A\otimes_{q} B)=A\otimes_{q} B\).
(ii)
\begin{align*} (A\oplus_{q} B)\vee_{q} (A\otimes_{q} B) &=\left[\left\langle \max\left\{ \left(\mu^q_{a_{ij}}+\mu^q_{b_{ij}}-\mu^q_{a_{ij}}\mu^q_{b_{ij}}\right)^{1/q},\mu_{a_{ij}}\mu_{b_{ij}}\right\},\min\left\{ \nu_{a_{ij}}\nu_{b_{ij}},\left(\nu^q_{a_{ij}}+\nu^q_{b_{ij}}-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q}\right\} \right\rangle\right]\\ &=\left[\left\langle \left(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q\right)^{1/q},\nu_{a_{ij}}\nu_{b_{ij}}\right\rangle\right]\\ &=A\oplus_{q} B.\end{align*} Hence, \((A\oplus_{q} B)\vee_{q} (A\otimes_{q} B)=A\oplus_{q} B.\)(iii)
\begin{align*} (A\oplus_{q} B)\wedge_{q} (A@B) &=\left[\left\langle\min\left\{\left(\mu^q_{a_{ij}}+\mu^q_{b_{ij}}-\mu^q_{a_{ij}}\mu^q_{b_{ij}}\right)^{1/q},\left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q}\right\},\max\left\{\nu_{a_{ij}}\nu_{b_{ij}},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle\left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\rangle\right]\\ &=A@B.\end{align*} Hence, \((A\oplus_{q} B)\wedge_{q} (A@B)=A@B.\)(iv)
\begin{align*} (A\oplus_{q} B)\vee_{q} (A@B) &=\left[\left\langle \max \left\{\left(\mu^q_{a_{ij}}+\mu^q_{b_{ij}}-\mu^q_{a_{ij}}\mu^q_{a_{ij}}\right)^{1/q},\left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q}\right\},\min\left\{\nu_{a_{ij}}\nu_{b_{ij}},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle \left(\mu_{a_{ij}}^q+\mu_{b_{ij}}^q-\mu_{a_{ij}}^q\mu_{b_{ij}}^q\right)^{1/q},\nu_{a_{ij}}\nu_{b_{ij}}\right\rangle\right]\\ &=A\oplus_{q} B.\end{align*} Hence, \((A\oplus_{q} B)\vee_{q} (A@B)=A\oplus_{q} B.\)(v)
\begin{align*} (A\otimes_{q} B)\wedge_{q} (A@B) &=\left[\left\langle\min\left\{\mu_{a_{ij}}\mu_{b_{ij}},\left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q}\right\},\max\left\{\left(\nu^q_{a_{ij}}+\nu^q_{b_{ij}}-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle \mu_{a_{ij}}\mu_{b_{ij}}, \left(\nu^q_{a_{ij}}+\nu^q_{b_{ij}}-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q}\right\rangle\right]\\ &=A\otimes_{q} B.\end{align*} Hence, \((A\otimes_{q} B)\wedge_{q} (A@B)=A\otimes_{q} B.\)(vi)
\begin{align*} (A\otimes_{q} B)\vee_{q} (A@B) &=\left[\left\langle\max\left\{\mu_{a_{ij}}\mu_{b_{ij}},\left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q}\right\},\min\left\{\left(\nu^q_{a_{ij}}+\nu^q_{b_{ij}}-\nu^q_{a_{ij}}\nu^q_{b_{ij}}\right)^{1/q},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\}\right\rangle\right]\\ &=\left[\left\langle \left(\dfrac{\mu^q_{a_{ij}}+\mu^q_{b_{ij}}}{2}\right)^{1/q},\left(\dfrac{\nu^q_{a_{ij}}+\nu^q_{b_{ij}}}{2}\right)^{1/q}\right\rangle\right]\\ &=A@B.\end{align*} Hence, \((A\otimes_{q} B)\vee_{q} (A@B)=A@B.\)Remark 1. The q-rung orthopair fuzzy matrix forms a commutative monoid, associativity, commutativity and identity under the q-rung orthopair fuzzy matrix operation of algebraic sum and algebraic product. The distributive law also holds for \(\oplus_{q}, \otimes_{q}\) and \(\wedge_{q}, \vee_{q}, @\) are combined each other.