Let \(G=(V;E)\) be a simple connected graph. The Sanskruti index was introduced by Hosamani and defined as \(S(G)=\sum_{uv \in E(G)}(\frac{S_uS_v}{S_u+S_v-2})^3\) where \(S_u\) is the summation of degrees of all neighbors of vertex \(u\) in \(G\). In this paper, we give explicit formulas for the Sanskruti index of an infinite class of Titania nanotubes \(TiO_2[m, n]\).
Let \(G=(V;E)\) be a simple connected graph. In chemical graph theory, the sets of vertices and edges of \(G\) are denoted by \(V=V(G)\) and \(E=E(G)\), respectively. A molecular graph is a simple finite graph such that its vertices correspond to the atoms and the edges to the bonds. A general reference for the notation in graph theory is [1, 2, 3].
In chemical graph theory, we have many different topological index of arbitrary molecular graph \(G\). A topological index of a graph is a number related to a graph which is invariant under graph automorphisms. Obviously, every topological index defines a counting polynomial and vice versa.
A graph can be recognized by a numeric number, a polynomial, a sequence of numbers or a matrix which represents the whole graph, and these representations are aimed to be uniquely defined for that graph. A topological index is a numeric quantity associated with a graph which characterizes the topology of the graph and is invariant under graph automorphism. There are some major classes of topological indices such as distance based topological indices, degree based topological indices and counting related polynomials and indices of graphs. Among these classes degree based topological indices are of great importance and play a vital role in chemical graph theory and particularly in chemistry.
Among topological descriptors, connectivity indices are very important and they have a prominent role in chemistry. One of the best known and widely used is the connectivity index \(R(G)=\sum_{uv \in E(G)} \frac{1}{\sqrt{d_ud_v}}\) introduced in 1975 by Milan Randić (see [4]), who has shown this index to reflect molecular branching.
The Sanskruti index \(S(G)\) of a graph \(G\) is defined as follows (see [5]):
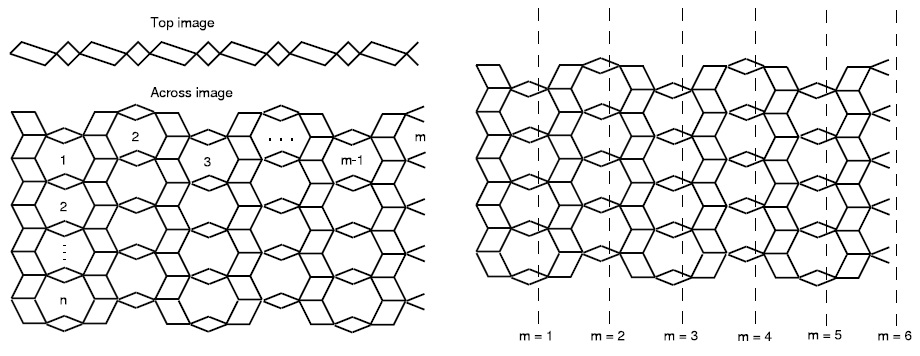
As a well-known semiconductor with numerous technological applications, Titania is comprehensively studied in materials science. Titania nanotubes were systematically synthesized during the last 10-15 years using different methods and carefully studied as prospective technological materials. Since the growth mechanism for \(TiO_2\) nanotubes is still not well defined, their comprehensive theoretical studies attract enhanced attention. \(TiO_2\) sheets with a thickness of a few atomic layers were found to be remarkably stable [12]. Recently Malik and Imran [13] and some others researchers computed multiple Zagreb index of \(TiO_2\) nanotubes, readers can see the paper series [14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27].
The graph of the Titania nanotube \(TiO_2[m, n]\) is presented in Fig. 1 where \(m\) denotes the number of octagons in a row and \(n\) denotes the number of octagons in a column of the Titania nanotube.
Let us define the partitions for the vertex set and the edge set of the Titania nanotube \(TiO_2\), for \(\delta(G)\leq k\leq \Delta(G)\), \(2\delta(G)\leq i\leq 2\Delta(G)\), and \(\delta(G)^2\leq j\leq \Delta(G)^2\), then we have [28]
$$V_k=\{v\in V(G)|deg(v)=k\},$$ $$E_i=\{e=uv\in E(G)|d(u)+d(v)=i\}.$$ In the molecular graph of \(TiO_2\)-nanotube, we can see that \(2\leq d(G)\leq5\). So, we have the vertex partitions as follows.| Edge partition | \(E_6\) | \(E_7\) | \(E_8\) |
|---|---|---|---|
| Cardinality | \(6n\) | \(4mn+4n\) | \(6mn-2n\) |
| \((S_u,S_v)\) where \(uv\in E(TiO_2[m,n])\) | (10,5) | (7,5) | (7,9) | (8,9) | (10,9) | (11,9) |
|---|---|---|---|---|---|---|
| Numbers of edges | \(2\) | \(2\) | \(2n\) | \(4n\) | \(2n\) | \(6m\) |
| \((S_u,S_v)\) \(\forall uv\in E(TiO_2[m,n])\) | (13,9) | (7,13) | (10,13) | (11,13) | (13,13) |
|---|---|---|---|---|---|
| Numbers of edges | \(3m\) | \(2n\) | \(4mn+2n\) | \(2mn-2n\) | \(6mn-4n\) |
Theorem 2.1. The Sanskruti index \(S(G)\) of Titania nanotube \(G=TiO_2[m,n]\) is given by $$S(G)=\frac{1753571}{8788}-\frac{5732099098294657}{19655694576000}n+\frac{12790839}{8000}m+\frac{8788000}{9261}mn+\frac{6092281}{2304}mn.$$
Proof. To compute the Sanskruti index \(S(G)\) of Titania nanotube \(TiO_2[m, n]\), we need an edge partition of the Titania nanotube \(TiO_2[m, n]\), based on degree sum of neighbors of end vertices of each edge. We presented these partitions with their cardinalities in Tables 2 and 3. Now using Eq. (1) and Tables 2 and 3 we get the required result as follows. \begin{eqnarray*} S(TiO_2[m, n])&=& \sum_{uv \in E(G)} (\frac{S_uS_v}{S_u+S_v-2})^3\\ &=&2(\frac{10\times5}{10+5-2})^3+2(\frac{7\times5}{7+5-2})^3+2n(\frac{7\times9}{7+9-2})^3\\ &&+4n(\frac{8\times9}{8+9-2})^3+2n(\frac{10\times9}{10+9-2})^3+6m(\frac{11\times9}{11+9-2})^3\\ &&+3m(\frac{13\times9}{13+9-2})^3+2n(\frac{7\times13}{7+13-2})^3+(4mn+2n)(\frac{10\times13}{10+13-2})^3\\ &&+(2mn-2n)(\frac{10\times5}{10+5-2})^3+2(\frac{10\times5}{10+5-2})^3\\ &=&\frac{1753571}{8788}-\frac{5732099098294657}{19655694576000}n+\frac{12790839}{8000}m\\ &&+\frac{8788000}{9261}mn+\frac{6092281}{2304}mn. \end{eqnarray*} The proof of theorem is completed.