The Generalized Zagreb Index of Capra-Designed Planar Benzenoid Series \(Ca_k(C_6)\)

1. Introduction

Let \(G=(V,E)\) be a simple connected graph of finite order \(n=|V|=|V(G)|\) with the set of vertices and the set of edges \(E=E(G)\). We denote by \(d_v\), the degree of a vertex \(v\) of \(G\) which is defined as the number of edges incident to \(v\). A general reference for the notation in graph theory is [1]. A molecular graph is a simple finite graph such that its vertices correspond to the atoms and the edges to the bonds.

In chemistry, graph invariants are known as topological indices. In graph theory, we have many different topological indices of arbitrary graph \(G\). A topological index of a graph is a number related to a graph which is invariant under graph automorphisms. Obviously, every topological index defines a counting polynomial and vice versa.

The Wiener index \(W(G)\) is the oldest based structure descriptor [2, 3, 4], introduced by Harold Wiener in 1947, is the first topological index in chemistry. The Wiener index of \(G\) is defined as the sum of distances between all pairs of vertices of \(G\) and is equal as follow: \begin{eqnarray*}\label{F1} W(G) &=& \frac{1}{2} \sum \limits_{(u,v)} d(u,v). \end{eqnarray*} where \((u,v)\) is any ordered pair of vertices in \(G\) and \(d(u,v)\) is \(u-v\) geodesic.

The Zagreb index was defined about forty years ago by I. Gutman and N. Trinajstic in 1972 [5] (or, more precisely, the First Zagreb index, because there exists also a Second Zagreb index [4]). The First Zagreb index of \(G\) is defined as the sum of the squares of the degrees of all vertices of \(G\) [6,7]. The first and second Zagreb indices of \(G\) are denoted by \(M_1(G)\) and \(M_2(G)\), respectively and defined as follows: \begin{eqnarray*} M_1(G) &=& \sum_{u \in V(G)} d_u^2 \hspace{10mm} \mbox{and} \hspace{10mm}\\ M_2(G) &=& \sum_{uv \in E(G)} d_{u}d_{v}. \end{eqnarray*} In fact, one can rewrite the first Zagreb index as $$M_1(G)=\sum_{uv \in E(G)} \big[ d_u+d_v \big].$$ where \(d_u\) and \(d_v\) are the degrees of \(u\) and \(v\), respectively. In 2011, M. Azari and A. Iranmanesh [8] introduced the generalized Zagreb index of a connected graph \(G\), based on degree of vertices of \(G\). The Generalized Zagreb index of \(G\) is defined for arbitrary non-negative integer \(r\) and \(s\) as follows: $$M_{(r,s)}(G)=\sum_{uv \in E(G)} \big[ d_u^rd_v^s+d_u^sd_v^r \big].$$

In [8], A. Iranmanesh and M. Azari expressed some of the obvious properties of the Generalized Zagreb index of a graph \(G\).

Theorem 1.1. [8] Let \(G\) be a graph with the vertex and edge sets \(V(G)\) and \(E(G)\). Some of the properties of the generalized Zagreb index of \(G\) are as

1. \(M_{(0,0)}(G)=2\sum_{v \in V(G)}=2|E(G)|\).
2. \(M_{(1,0)}(G)=M_1(G)\).
3. \(M_{(r-1,0)}(G)=\sum_{v \in V(G)}dv^r\).
4. \(M_{(1,1)}(G)=2M_2(G)\).
5. \(M_{(r,r)}(G)=2 \sum_{uv \in E(G)}(d_u\times d_v)^r\).

2. What is the Capra Operation?

A mapping is a new drawing of an arbitrary planar graph \(G\) on the plane. In graph theory, there are many different mappings (or drawing); one of them is Capra operation. This method enables one to build a new structure of a planar graph \(G\).

Let \(G\) be a cyclic planar graph. Capra map operation is achieved as follows:

1. insert two vertices on every edge of \(G\);
2. add pendant vertices to the above inserted ones and
3. connect the pendant vertices in order \((-1,+3)\) around the boundary of a face of \(G\). By runing these steps for every face/cycle of \(G\), one obtains the Capra-transform of \(G\) \(Ca(G)\), see Figure 1.

By iterating the Capra-operation on the hexagon (i.e. benzene graph \(C_6\)) and its \(Ca-\)transforms, a benzenoid series (Figures 2 and 3) can be designed. We will use the Capra-designed benzene series to calculate some connectivity indices (see below).

This method was introduced by M.V. Diudea and used in many papers [9, 10, 11, 12, 13, 14, 15, 16]. Since Capra of planar benzenoid series has a very remarkable structure, we lionize it.

We denote Capra operation by \(Ca\), in this paper, as originally Diudea did. Thus, Capra operation of arbitrary graph \(G\) is \(Ca(G)\), iteration of Capra will be denoted by \(CaCa(G)\) (or we denote \(Ca_2(G))\) (Figures 2 and 3).

The benzene molecule is a usual molecule in chemistry, physics and nano sciences. This molecule is very useful to synthesize aromatic compounds. We use the Capra operation to generate new structures of molecular graph benzene series.

In this paper, we focus on the the structure of Capra-designed planar benzenoid series \(Ca_k(C_6)\), \(k\geq0\) and compute its generalized Zagreb index.

The aim of this paper is to compute the generalized Zagreb index \(M_{(r,s)}\)(G) of Capra-designed planar benzenoid series \(Ca_k(C_6)\).

3. Main Results

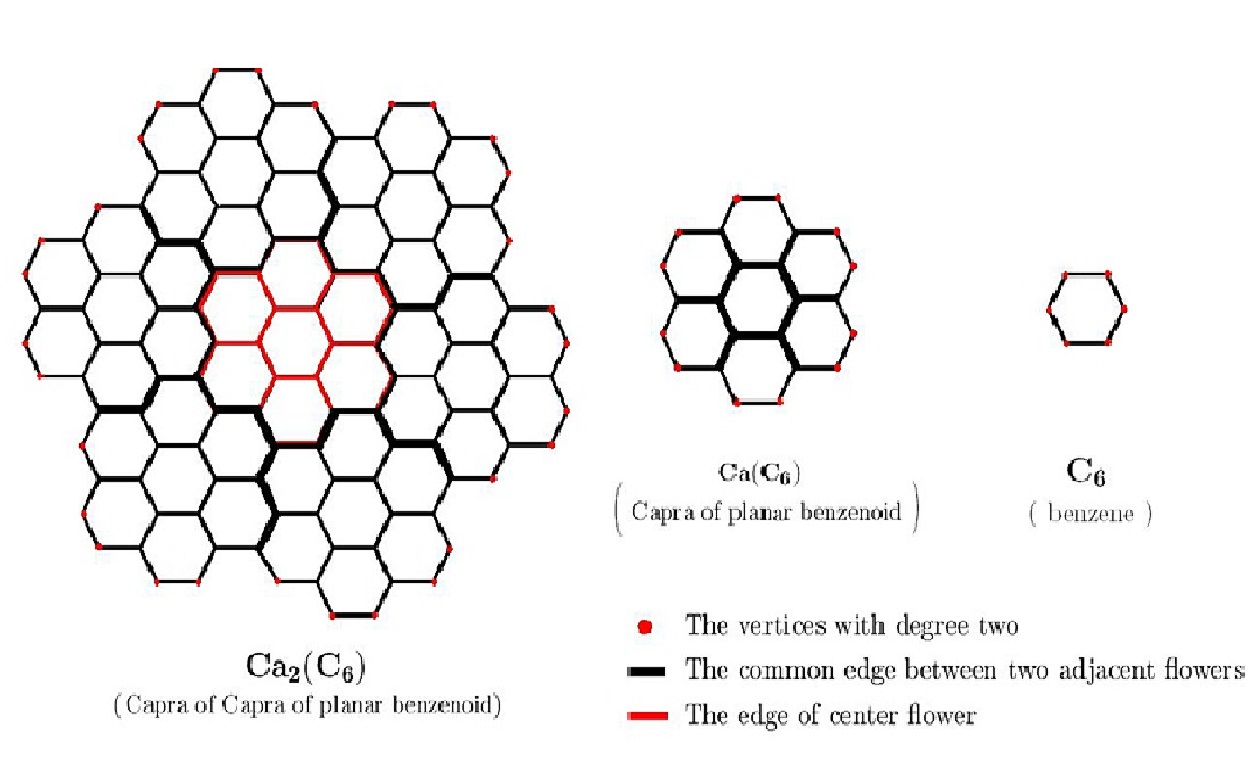
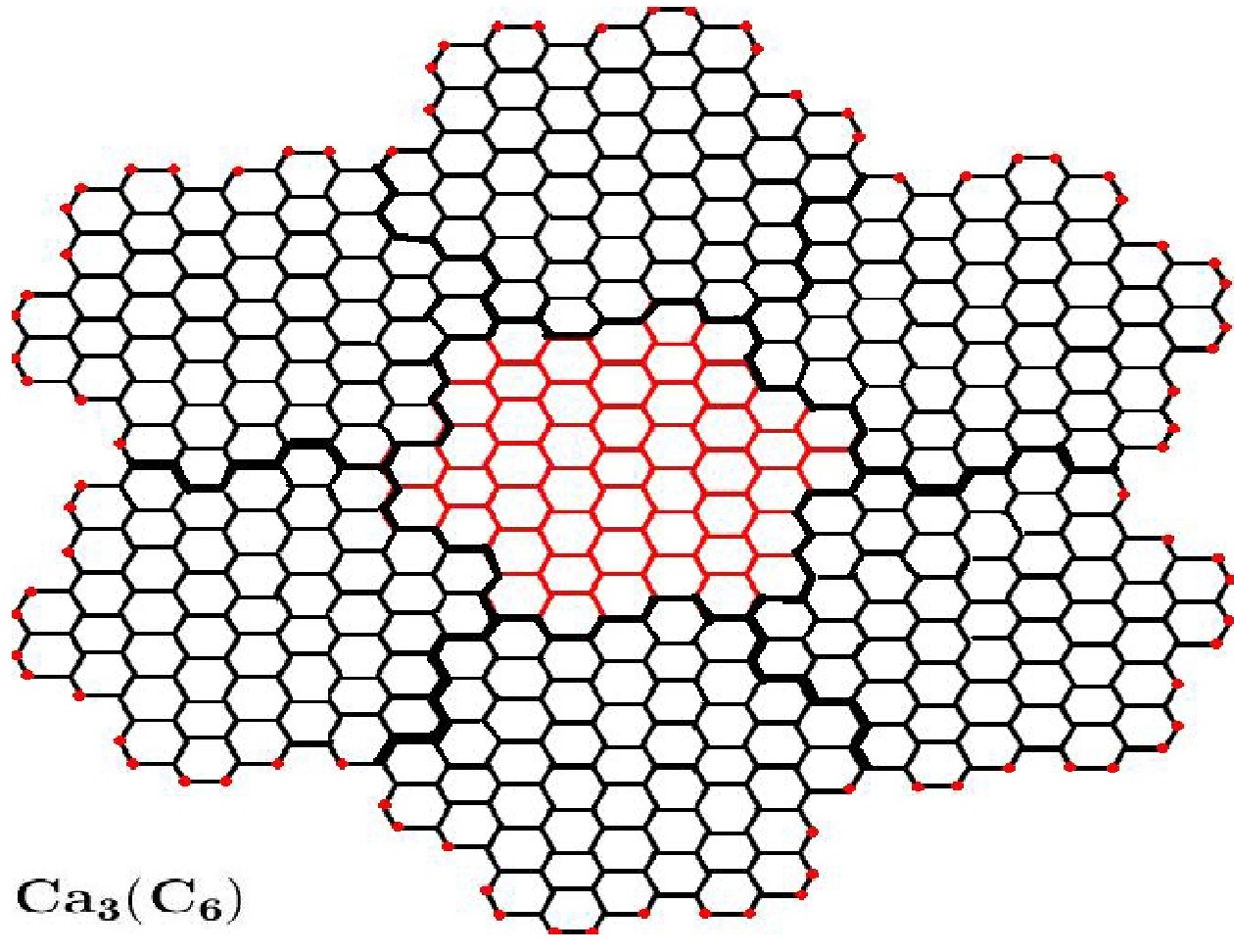
Capra transforms of a planar benzenoid series is a family of molecular graphs which are generalizations of benzene molecule \(C_6\). In other words, we consider the base member of this family is the planar benzene, denoted here \(Ca_0(C_6)=C_6=\) benzene. It is easy to see that \(Ca_k(C_6)=Ca(Ca_{k-1}(C_6))\) (Figures 2 and 3) ([9, 10, 11, 12, 13, 14, 15, 16]). In addition, we need the following notions [17]. Let \(G\) be a molecular graph and \(d_v\) is the degree of vertex \(v\in V(G)\). We divide vertex set \(V(G)\) and edge set \(E(G)\) of graph \(G\) to several partitions, as follow:

\(\forall i\), \(\delta < i< \Delta\), \(V_i=\{v \in V(G) |d_v=i\}\),
and \(\forall k, \delta^2\leq k\leq \Delta^2, E^*_k=\{e=uv\in E(G)|d_v\times d_u=k\}\).
Obviously, \(1\leq\delta\leq d_v\leq\Delta\leq n-1\) such that \(\delta=Min\{d_v|v\in V(G)\}\) and \(\Delta=Max\{d_v|v\in V(G)\}\).

Theorem 3.1. Consider the graph \(G=Ca_k(C_6)\) as the iterative Capra of planar benzenoid series. Then: $$ M_{(r,s)}=3(7^k-2(3^{k-1})-1)\times \big[ 2(3^{r+s}) \big]+4(3^k) \times\big[ 2^r3^s+2^s3^r \big]+3(3^{k-1}+1)\times \big[2(2^{r+s}) \big]. $$

Proof. Consider the Capra of planar benzenoid series \(G=Ca_k(C_6)\) \((k\geq1)\). By construction, the structure \(Ca_k(C_6)\) collects seven times of structure \(Ca_k-1(C_6)\) (we call “flower” the substructure \(Ca_{k-1}(C_6)\) in the graph \(Ca_k(C_6))\). Therefore, by simple induction on \(k\), the vertex set of \(Ca_k(C_6)\) will have \(7\times|V(Ca_k(C_6))|-6(2\times3^{k-1}+1)\) members. Because, there are \(3^{k-1}+1\) and \(3^{k-1}\) common vertices between seven flowers \(Ca_{k-1}(C_6)\) in \(Ca_k(C_6)\), marked by full black color in the above figures. Similarly, the edge set \(E(Ca_k(C6))\) have \(7\times|E(Ca_k(C_6))|-6(2×3^{k-1}+1)\) members. Since, there are \(3^{k-1}\) and \(3^{k-1}\) common edges (full black color in these figures).
Now, we solve the recursive sequences \(|V(Ca_k(C_6))|\) and \(|E(Ca_k(C_6))|\). First, suppose \(n_k=|V(Ca_k(C_6))|\) and \(e_k=|E(Ca_k(C_6))|\)
so \(n_k=7n_{k-1}-4(3^k)-6\) and \(e_k=7e_{k-1}-4(3^k)\). Thus, we have
\(n_k=7n_{k-1}-4ò_k-6\)
\(=7(7n_{k-2}-4ò_{k-1}-6)-4ò_k-6\)
\(=7^2n_{k-2}-7(4ò_{k-1}+6)-(4ò_k+6)\)
\(=7^3n_{k-3}-7^2(4ò_{k-2}+6)-7(4ò_{k-1}+6)-(4ò_k+6)\)
.
.
.
\(=7^in_{k-i}-7^{i-1}(4ò_{k-(i-1)}+6)-…-7(4ò_{k-1}+6)-(4ò_k+6)\)
\(=7^in_{k-i}-\sum^{i-1}_{j=0}7^j(4ò_{k-j}+6)\)
.
.
.
\(=7^kn_{k-k}-\sum^{k-1}_{i=0}7^i(4ò_{k-i}+6)\)

where \(n_0=6\) is the number of vertices in benzene \(C_6\) (Figure 2) and \(6\sum^{k-1}_{i=0}7^i\) is equal to \(\frac{6(7^k-1)}{7-1}=7^k-1\). On the other hand, since
\((\alpha-\beta)\sum^n_{i=0}\alpha^i\beta^{n-1}=(\alpha-\beta)(\alpha^0\beta^n+\alpha^1\beta^{n-1}+…+\alpha^{n-1}\beta^1+\alpha^n\beta^0)=(\alpha^{n+1}-\beta^{n+1})\) Hence
\(\sum^{k-1}_{i=0}7^i3^{k-i}=(7^03^k+7^13^{k-1}+…+7^{k-2}3^2+7^{k-1}3^1)+7^k3^0-7^k3^0\)
\(=\frac{7^{k+1}-3^{k+1}}{7^1-3^1}-7^k3^0\)
\(=\frac{7^{k+1}-3^{k+1}-4(7^k)}{4}\)
\(=\frac{3(7^k-3(3^k))}{4}\) Therefore, by using equations (1) and (2), we have
\(n_k=6\times7^k-(4(\frac{3}{4}(7^k-3^k))+(7^k-1))\) and \(\forall k\geq0, n_k=|V(Ca_k(C_6))|=2\times7^k+3^{k+1}+1. \)
By using a similar argument and (1), we can see that
\(e_k=7e_{k-1}-4ò=7^2e_{k-2}-7(4ò_{k-1})-4ò.\)
.
.
.
\(=7^ke_{k-k=0}-4\sum^{k-1}_{i=0}7^iò_{k-i}=7^ke_0-4\sum^{k-1}_{i=0}7^i3^{k-i}\).
It is easy to see that, the first member of recursive sequence \(e_k\) is \(e_0=6\), (Figure 2). Now, by using (2), we have \(e_k=6\times7^k-4(\frac{3}{4}(7^k-3^k))\) and the size of edge set \(E(Ca_k(C_6))\) is equal to: \(e_k=|E(Ca_k(C_6))|=3(^7k+3^k)\), \(\forall k\geq0\).
Also, according to Figures 2 and 3, we see that the number of vertices of degree two in the graph \(Ca_k(C_6)\) (we denote by \(v^{(k)}_2\) ) is equal to \(6\times3(\frac{(v_2^{(k-1))}}{6})-6\). The six removed vertices are the common ones between the six flowers \(“Ca_{k-1}(C_6)”\) with degree three. By using a similar argument and simple induction, we have \(v_2^{k-1}\) the numbers of edges of graph \(Ca_k(C_6)\), which are in the set \(E_4\) or \(E_4^*\) (denoted by \(e_4^{(k)}\)).
Now, we solve the recursive sequence \(v_2^{(k)}=6(3(\frac{v_2^{(k-1)}}{6})-1)\) and we conclude \(v_2^{k}=3v_2^{(k-1)}-6=3(3v_2^{(k-2)}-6)-6=…=3^kv_2^{(0)}-6\sum^{k-1}_{i=0}3^i\).
It is obvious that, according to the structure of benzene, \(v_2^{(0)}=n_0=6\). Thus, \(v_2^{(k)}=6\times3^k-6(\frac{3^k-1}{3-1})=3^k+1+3.\)
Also, \(e_4^{(k)}=|E_4|=|E_4^*|=v_2^{(k-1)}=3^{k+1}+3\) and according to the above definition, it is obvious that, for Capra of planar benzenoid series \(G=Ca_k(C_6)\) we have two partitions: \(V_2=\{v\in V(Ca_k(C_6))|d_v=2\}\) and \(V_3=\{v\in V(Ca_k(C_6))|d_v=3\}\) with the size \(3^{k+1}+3\) and \(2(7^k-1)\) respectively.
On the other hand, according to the structure of Capra planar benzenoid series \(Ca_k(C_6)\), there are \(2v_2^{(k)}\) edges, such that the first point of them is a vertex with degree two. Among these edges, there exist \(v_2^{k-1}\) edges, of which the first and end point of them have degree 2 (the members of \(E_4\) or \(E_4^*\) ).
Thus, \(e_5^{(k)}=|E_5|=|E_6^*|=2v_2^{(k)}-2e_4^{(k)}=2v_2^{(k)}-2v_2^{(k-1)}\). So, the size of edge set \(E_5\) and \(E_6^*\) is equal to \(e_5^{k}=2(3^{k+1}+3-3^k-3)=4(3^k)\).
Now, it is obvious that:
\(e_6^{(k)}=|E_6|=|E_9^*|=3(7^k+3^k)-e_5^{(k)}-e_4^{(k)}\)
\(=3\times7^k+3^{k+1}-4\times3^k-3^k-3\)
\(=3\times7^k-2\times3^k-3\)
\(={3(7^k-2(3^{k-1})-1)}.\)
Now, we know the size of all sets \(V_2, V_3, E_4, E_4^*, E_5, E_6^*, E_6\) and \(E_9^*\). So, we can calculate the Generalized Zagreb Index Of Capra planar benzenoid series \(G=Ca_k(C_6)\), as follow:
Thus, we have following computations for the generalized Zagreb index of Capra planar benzenoid series \(G=Ca_k(C_6)\) $$M_{(r,s)}(G)=\sum_{uv \in E(G)} \big[ d_u^rd_v^s+d_u^sd_v^r \big] $$ $$=\sum_{uv \in E(G)} \big[ 3^r3^s+3^s3^r \big]+\sum_{uv \in E(G)} \big[ 2^r3^s+2^s3^r \big]+\sum_{uv \in E(G)} \big[ 2^r2^s+2^s2^r \big] $$ $$=\sum_{uv \in E(G)} \big[ 2(3^{r+s}) \big]+\sum_{uv \in E(G)} \big[ 2^r3^s+2^s3^r \big]+\sum_{uv \in E(G)} \big[2(2^{r+s})\big] $$ $$=3(7^k-2(3^{k-1})-1)\times \big[ 2(3^{r+s}) \big]+4(3^k) \times\big[ 2^r3^s+2^s3^r \big]+3(3^{k-1}+1)\times \big[2(2^{r+s}) \big].$$ Thus, we completed the proof of the theorem.

Competing Interests

The author(s) do not have any competing interests in the manuscript.